高温高压条件下纳米材料强度的测试和分析方法

顾超，王善民，赵予生*

1 南方科技大学物理系，深圳 518055 2 南方科技大学前沿与交叉科学研究院，深圳 518055

0 引言

纳米晶材料是由纳米尺寸(<100 nm)晶粒所组成的材料.当晶体材料的晶粒大小或外形尺寸与特定的物理量相当时，如平均自由程、位错体积、铁磁畴、铁电畴或声子相干长度等，相应的物理现象将会发生明显的变化.因此，通过控制晶粒尺寸对晶体材料进行微观结构调控，有望产生新现象和行为，实现材料在性能上的革新.除了尺寸因素，纳米晶材料在微观结构上也不同于微晶材料，纳米晶体通常可以用核-壳(core-shell)模型来描述，即包括晶格完美的晶核部分和“无序”的表面原子层，其原子排列既不同于有序的晶态，也不同于无序的非晶态(玻璃态).当晶粒尺寸减小到纳米级时，壳层可占整个材料的50%甚至更多，由于纳米表层的原子构造和原子之间的键等都与完美晶体不同，其性能也不同于晶体或非晶体，因此，可通过尺寸效应对材料的性能进行调节.大量的实验研究表明，随着晶粒尺寸从微米减小到纳米级，材料的各种性能，如相稳定性(Chen et al.，1997)、熔化温度(Goldstein et al.，1992)、屈服强度(Chen et al.，2005；Wang et al.，2007)、弹性模量(Tolbert and Alivisatos，1995；Jiang et al.，1998；Wang et al.，2003，2004)、电子结构(van Buuren et al.，1998)等都会发生明显的改变.

目前，利用传统的力学测试方法难以研究纳米材料的变形机理和本征力学性能.以纳米晶材料的硬度研究为例，根据经典的Hall-Petch关系(Hall，1951；Petch，1953)，可以预测多晶材料的强度随着晶粒尺寸的减小而增加.虽然这种关系是根据经验建立起来的，但它在许多纳米晶体金属和合金中得到了验证(Chen et al.，2005；Qian et al.，2005；Zhao et al.，2007).Hall-Petch效应一般归因于位错在晶界处的塞积阻碍了塑性变形过程，使后续的位错运动需要更大的应力来开动，从而导致硬度等力学性能的提升.因此，在晶粒尺寸较小的材料中，晶界密度的增加会对位错运动造成更大的阻碍，宏观表现为强度或硬度的增加.然而，实验和分子动力学模拟结果表明(Chokshi et al.，1989；Lu et al.，1990；Palumbo et al.，1990；Chang et al.，1992；Khan et al.，2000)，在一些晶粒尺寸在3～20 nm范围内的金属和合金中，Hall-Petch关系并不适用.在这些材料中，当晶粒尺寸小于某一临界值时，硬度随着晶粒尺寸的减小而减小或保持不变，这种现象被称为反Hall-Petch效应.在一些情况下，实验观察到的反Hall-Petch效应可能并非是材料的本征性能，而是由于孔隙或夹杂物的存在使材料的强度或硬度下降.其中，屈服强度并不是材料的固有特性，它取决于材料的内部结构、化学成分以及加载条件.在纳米材料中，特定的化学组分或缺陷密度分布的差异，可以极大地改变材料的屈服强度.在具有高脆性和低韧性的陶瓷材料中，传统的压痕和拉伸试验方法都不适合研究陶瓷材料的尺寸效应，对本征纳米效应和变形机制的研究也十分匮乏.此外，对于三轴加载下纳米晶材料塑性变形的位错形核、扩展和塞积过程，以及它们随压力和温度的变化趋势，仍然没有很好的方法可以进行表征.

通过衍射峰宽分析材料的应变或强度是科学界广泛使用的一种经典方法，通常被称为Williamson-Hall法或其演化法(Williamson and Hall，1953；Gerward et al.，1976).该方法可以克服传统压痕或变形实验中常见的样品孔隙或杂质问题.一般来说，多晶衍射图谱是仪器参数、晶粒尺寸分布和晶格沿衍射矢量方向变形的卷积函数.在高压压缩实验中，衍射峰的宽化表明沿着衍射矢量方向的非均匀应变的分布(Weidner et al.,1994a)，这些应变源于不同晶体取向的晶粒在受力方向上的形变，以及在粉末压缩实验中晶粒间接触位置的应力集中.当偏应力接近屈服强度时，试样开始塑性流动，衍射峰宽度达到最大值.通过分析不同的hkl晶面衍射峰宽随压力的变化，可以得到不同的应变值，进而得到样品的屈服强度.基于以上方法，为了更好地理解纳米材料的力学性能和变形机理，尤其是在高温高压下的变形行为，我们进行了一系列的同步辐射X射线衍射和中子衍射实验来研究纳米材料的本征特性.为了准确地表征纳米材料的独特性能，我们使用相同的技术研究了纳米晶和微米晶材料，并在某些情况下，将这两种材料在同一个高温高压实验中进行直接比较.本文使用的方法可以用于岩石矿物的高温高压流变强度的定量测定，通过该方法测定的流变实验结果可以为评估中上地壳流变结构，与发生在中上地壳的地震及其余震深度分布规律提供实验数据支持，为反映大陆中上地壳的真实情况提供新的研究方法，为研究岩石圈以及地幔物质的蠕变对流提供了高科技的研究手段.

1 材料与方法

镍(Ni)是一种具有重要技术意义的3d过渡金属.纳米晶Ni一直是许多实验和理论工作的重点研究载体.在前期的研究中，纳米晶Ni的力学、电学、磁性、弹性和扩散系数等性质已经得到了广泛的研究(Bonetti et al.，1999;Chen et al.，2000；Rekhi et al.，2001；Budrovic et al.，2004；Shan et al.，2004).本研究选用微米晶和纳米晶Ni粉为研究对象，微米晶Ni粉的纯度为99.8%，粒度分布为3～7 μm，纳米晶Ni粉是通过将商业微米晶Ni粉(Alfa Aesar, 99.999%)进行高能球磨制备的.球磨时将5 g镍粉和30个质量为1 g的淬火钢球放入球磨罐，用SPEX 8000球磨机研磨30小时.球磨过程是在具有氩气环境的手套箱中操作的，手套箱中氧气含量小于1×10-6.通过差示扫描量热法(Differential Scanning Calorimetry，DSC)(Shen et al.，1995)测定居里转变温度表明，制备的纳米晶Ni中含有约1 at%的铁杂质.根据X射线衍射峰宽分析，纳米晶Ni粉的平均晶粒尺寸为12～13 nm.两种Ni粉的中子衍射谱在布拉格角为40°、90°和150°位置均未发现择优取向.高压X射线衍射实验是在美国布鲁克海文国家实验室的国家同步光源X17B2线站上进行的.实验选择六面顶压砧装置对样品进行加压和升温(Weidner et al.，1992)，为了进行对比实验，纳米晶和微米晶Ni被放置在同一个氮化硼管中，中间由NaCl隔开.除了隔离样品，NaCl也同时作为内标压物质，通过Decker状态方程对NaCl进行压力标定(Decker，1971).常压下的飞行时间中子衍射实验(time-of-flight, TOF)是在美国洛斯阿拉莫斯国家实验室HIPPO(High-Pressure Preferred Orientation)光束线上进行的(Wenk et al.，2003).

2 纳米晶材料的力学性能测试与分析

2.1 纳米晶Ni的弹性软化

在目前对纳米晶材料的性能研究中，晶粒尺寸对材料弹性性能的影响仍然是一个有争议的问题.例如，在早期的研究中发现，纳米晶材料的杨氏模量值远远低于与之对应的微米晶材料(Gleiter，1989).尽管这种软化现象在一定程度上可以归因于制备的材料中存在较大体积分数的孔隙和微裂纹，但随后基于无孔隙纳米晶样品的实验和理论计算(Shen et al.，1995)结果仍然表明，当晶粒尺寸小于20 nm时，材料显示出了明显的弹性软化现象.与之相反，在一些使用X射线衍射进行表征的压缩实验中，纳米晶材料的体弹模量高于常规微米晶材料(Tolbert and Alivisatos，1995；Jiang et al.，1998;Wang et al.，2003，2004).此外，在Fe、Ni、MgO和CuO等材料中，压缩性能又显示出了与晶粒尺寸无关的现象(Chen et al.，2000；Rekhi et al.，2001；Zhang et al.，2007；Chen et al.，2008).以上研究结果表明，晶粒尺寸对材料弹性性能的影响可能不存在一个普适性的规律，其中一些研究的结论可能是不确定的.原因有两方面，一方面是这些实验研究大多只关注纳米晶材料本身，并没有与早期研究的常规材料数据进行对比，从而忽略了不同测试技术中系统误差造成的影响；另一方面，纳米晶的弹性变形行为过于微小，无法用常规的实验方法来检测.为了解决这些问题，我们利用同步辐射X射线衍射对装载在同一腔体内的纳米晶和微米晶Ni进行了高压压缩性能研究(Zhang et al.，2007).这种方法可以消除仪器响应和压力/偏应力测定所产生的系统误差，从而可以检测出二者在压缩过程中的微小差异(Hazen，1993；Zhang et al.，2013).

纳米晶和微米晶Ni在常压和7.4 GPa(实验的最高压力)下的X射线衍射(XRD)图谱如图1所示.由于在高能球磨细化晶粒过程中引入了表面应变效应，纳米晶Ni的晶格常数略大于微米晶Ni的.此外，球磨过程引入的Fe杂质也会使衍射峰向更大的d值方向偏移(McKeehan，1923).从图1中可以看出，纳米晶Ni的衍射峰明显比微米晶Ni的衍射峰宽.这种宽化一方面来自于晶粒细化，另一方面源于球磨过程中产生的位错导致晶体中缺陷密度增加，从而引入了微观晶格应变.

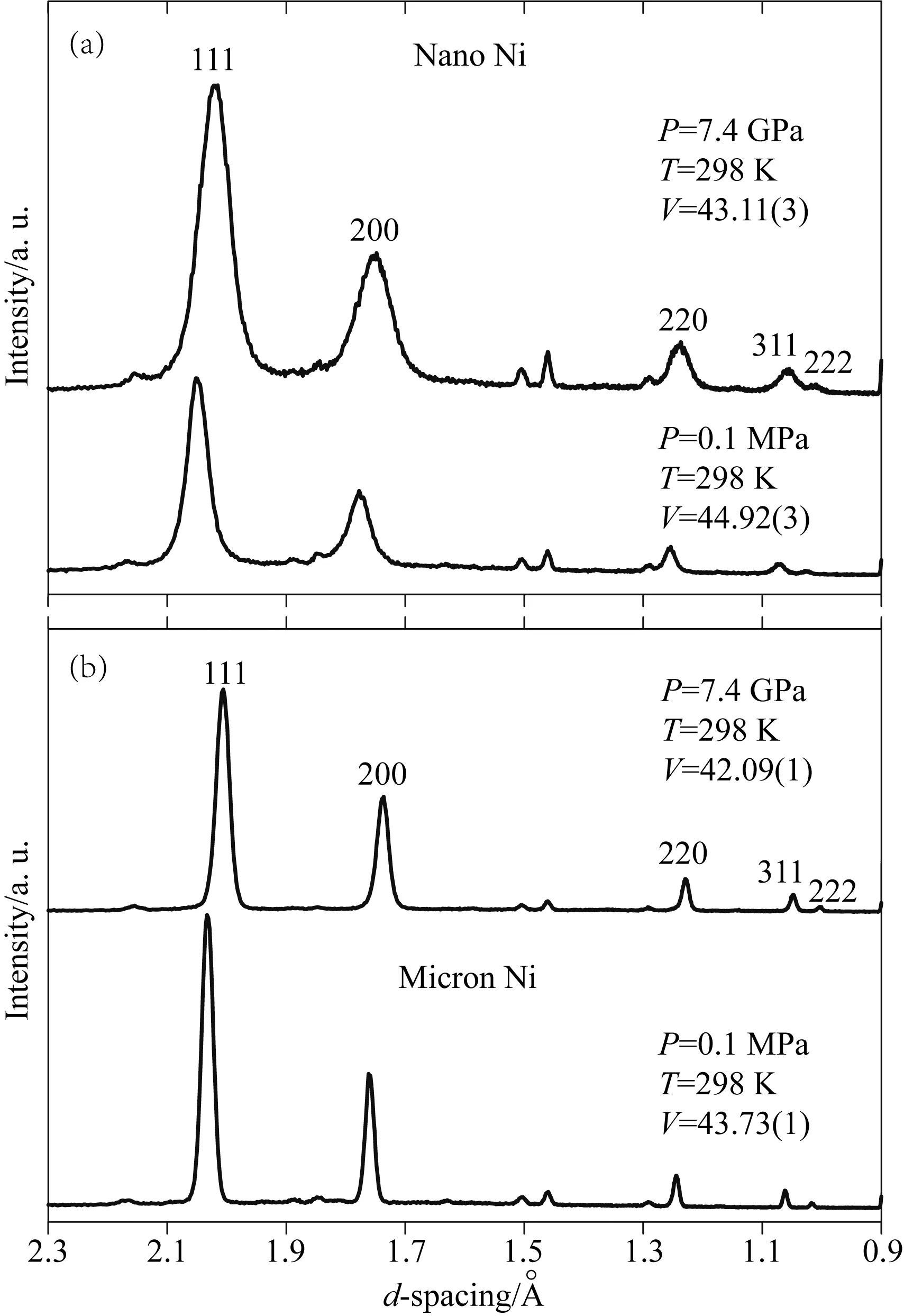
图1 (a)纳米和(b)微米Ni在298 K和选定压力下的X射线衍射图谱

利用实验得到的衍射图谱，首先通过衍射峰强度的高斯拟合确定了衍射峰位置，然后利用纳米晶和微米晶Ni的111、200、220、311和222衍射峰，基于立方晶胞的最小二乘法拟合计算得出了纳米晶和微米晶Ni的单胞体积(V)，其标准偏差分别为0.05%～0.1%和0.02%～0.03%.纳米晶和微米晶Ni的晶胞压缩率V/V0(V0为常压下的晶胞体积)随压力变化的趋势如图2所示.从图2中可以看出，纳米晶Ni比微米晶Ni的抗压缩性能更差.

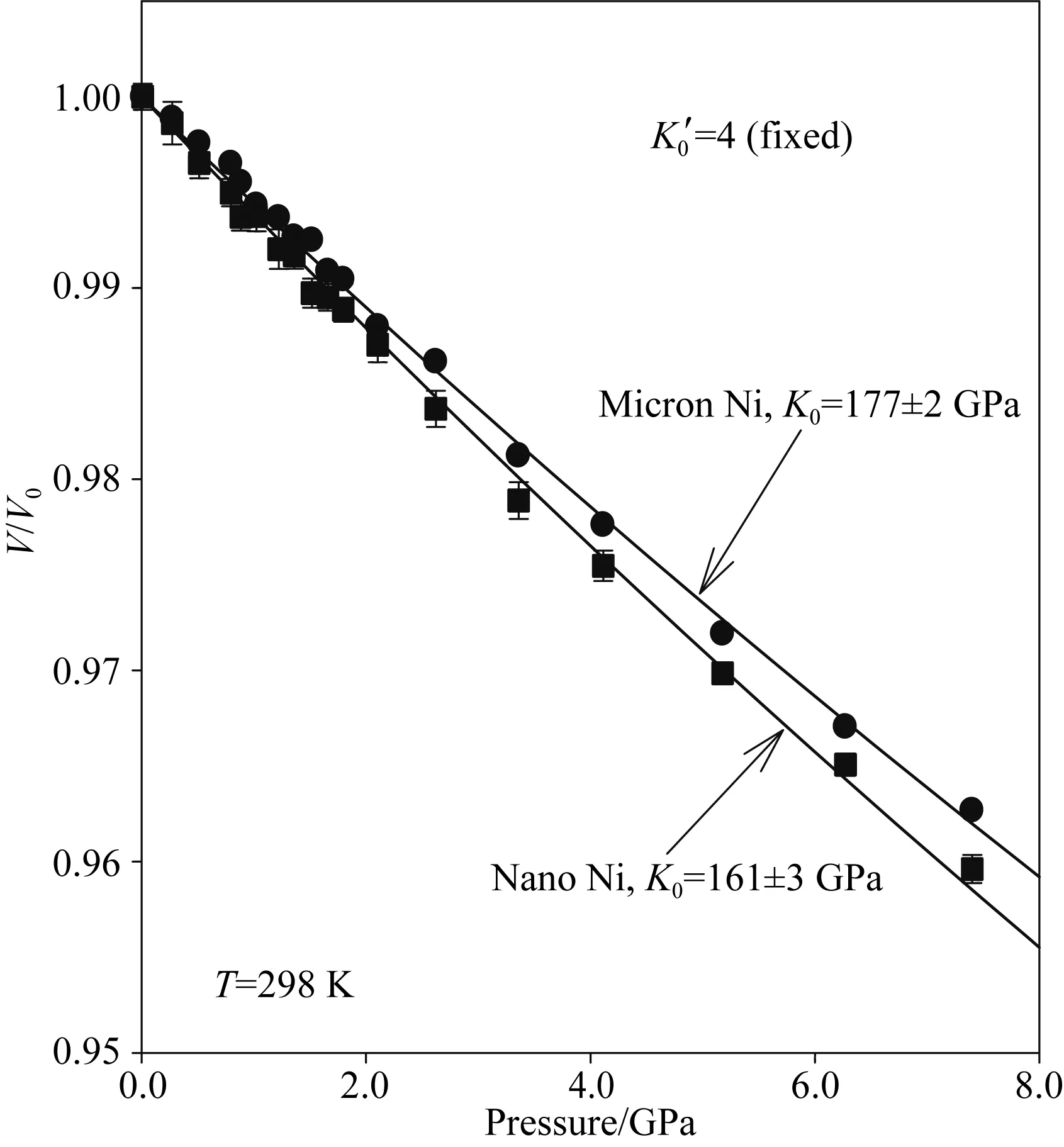
图2 归一化单胞体积V/V0随压力的变化关系

为了对二者的体弹模量进行定量比较，使用欧拉有限应变状态方程(Birch，1978)对图2的数据进行拟合.在状态方程中，压强P可表示为应变f的三阶方程：

P=3f(1+2f)5/2·K0[1-2ξf+…]，

(1)

其中，

式中，K0和K′0分别为绝热体弹模量及其在环境温度下关于压力的导数.由于本实验压力范围有限，对K′0影响较小，故可采用二阶状态方程对体弹模量进行计算，即式(1)中ξ= 0.此时对图2所示数据进行拟合，可得纳米晶和微米晶Ni的体弹模量分别为K0=161±3 GPa和K0=177±2 GPa.该结果表明，纳米晶Ni比微米晶Ni的可压缩性高约10%.

在早期的研究中，Chen等(2000)利用X射线衍射和金刚石对顶砧技术研究了纳米晶Ni的压缩性能，根据晶格体积从常压到55 GPa的变化趋势，计算得出纳米晶Ni的体弹模量为185.4±10 GPa，与之前报道的微米晶Ni的体弹模量180 GPa接近.在另一项研究中，Rekhi等(2001)通过实验和第一性原理计算分别得到了纳米晶Ni(K0=228±15 GPa)和微米晶Ni(K0=217 GPa)的体弹模量，结果表明二者数值相当.与我们目前的实验结果不同，这两项研究都得出晶粒尺寸对Ni的压缩性能没有影响.然而，无论在实验或理论计算中，都会有系统误差存在，在对不同方法得到的体弹模量数值进行比较时，由于系统误差的影响，会增加结果的不确定性.本研究采用的实验方法可以消除压力和偏应力这两个变量的误差，更适用于压缩性能中细微差异的检测.

纳米晶材料由于表层原子密度降低，压缩性通常会增加(Gleiter，1989；Trapp et al.，1995).然而，到目前为止，基本没有关于纳米晶表面原子排列的具体信息，也没有实验方法可以直接区分表面区域和晶体内部之间的压缩行为.Palosz等(2002)在一系列研究中表明，对于纳米晶材料，很难从布拉格衍射峰的位置的变化中得到晶格参数，从而无法得到有效的体弹模量.由此，他们提出了一种纳米晶粉末衍射数据的分析方法，该方法基于单个布拉格衍射峰计算晶格常数，并称之为“表观晶格常数”(apparent lattice parameters，alp)，在数值上与Q=2π/d相关，其中d为hkl衍射峰对应的晶面间距，单位为Å.理论计算和实验结果都表明alp值与Q具有复杂的相关性，并具有一定的特征极小值和极大值.仔细分析这些特征就有可能揭示纳米晶的晶体结构和特征，特别是表面层的结构和变形行为.根据Palosz的分析，在很大的Q值下观测到的衍射数据可以用来研究晶核的性质(即纳米晶核的真实晶格常数)，而在较小的Q值下观测到的衍射数据则对晶粒表面(即壳层)的结构信息更加敏感.

基于alp的概念，在目前的实验结果中根据不同的衍射峰分别计算了纳米晶和微米晶Ni的单胞体积(alp)3，并用公式(1)对其进行拟合，得到与Q值相对应的体弹模量如图3所示.对于微米晶Ni，通过不同衍射峰得到的体弹模量数值基本相同，与Q值无相关性；对于纳米晶Ni，在Q= 3.1～3.5 Å-1时的体弹模量明显低于Q= 5.0～5.9 Å-1时的数值(减小约10%).由于粉末X射线衍射实验可获得的Q值范围有限，实验得到Ni的Q值范围较窄(≈ 3～6 Å-1)，无法准确地确定晶格常数，从而无法准确地确定晶核的压缩性能.然而，对于具有表面壳层应变(膨胀)的纳米晶广义模型(Palosz et al.,2002;Zhang et al.,2007;Chen et al.,2008)(如图3中的插图所示)，我们的研究表明纳米晶Ni的表面层比晶粒内部的可压缩性更强.据此还可以推断，与晶粒内部相比，表面壳层具有某种膨胀结构，原子间距离更长.

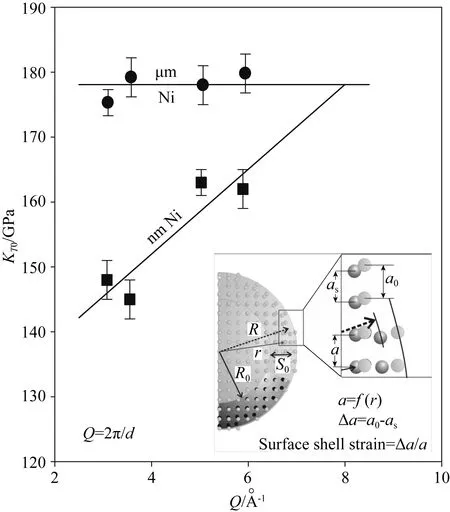
图3 不同衍射矢量Q下纳米晶和微米晶的体弹模量.体弹模量数值通过“表观晶格常数”由单独的布拉格衍射峰计算得出

有研究者利用分子动力学模拟研究了纳米晶Ni体弹模量的晶粒尺寸依赖性(Zhao et al.，2006)，计算的P-V数据表明纳米晶Ni比单晶Ni的体弹模量减小了7%，与我们的研究结果十分接近.如果将块体纳米晶的体弹模量表示为晶粒表面壳层和内部核的模量组合，利用一个简单的混合定则模型可以得出在286 K时表面壳层的体弹模量比晶粒内核小9.2%，该结果也与我们的实验结果一致.因此，实验和理论计算都表明，纳米晶Ni的“整体”抗压缩性的减小是晶粒表面壳层抗压缩性减小的结果.我们的研究表明，将粉末衍射与压缩实验相结合的方法是探索纳米材料表面壳层结构和行为的有效手段.

2.2 纳米晶Ni的表观应变和晶粒尺寸计算方法

屈服强度(σy)是材料的一个重要性能指标，用来定义塑性变形和黏滞流动的开始阶段，通常由材料的应力-应变曲线测量来确定.高强度同步辐射X射线衍射技术和飞行时间中子衍射技术则可以实现在原子尺度上对块体样品进行形变研究(Weidner et al.,1994a；Zhang et al.，2002；Brown et al.，2003；Qian et al.，2005).基于经典的Williamson-Hall方法及其后续演化方法(Williamson and Hall，1953；Gerward et al.，1976；Weidner et al.,1994b；Révész et al.，1996；Ungár and Borbély，1996；Ungár and Tichy，1999)，可以从衍射数据的峰宽分析中得到应变、强度、位错密度和晶粒尺寸等信息.我们对纳米晶和微米晶Ni进行了3次高压同步辐射X射线衍射实验和2次高温中子衍射实验.在所有的同步辐射X射线衍射实验中，纳米晶和微米晶Ni被装入同一样品腔，以便直接和准确地对比二者的性能差异.在中子衍射实验中，将Ni粉装入直径为6.35 mm的钒管中，在真空条件下进行原位加热，温度范围为318～1073 K，每个衍射图谱的采集时间为2 h.图4和图5分别为选定压力和温度下的同步辐射X射线衍射和中子衍射图谱，显示了不同温压条件下峰宽的变化.

图4 (a)纳米晶和(b)微米晶Ni在298 K和选定压力下，从单次高压实验得到的同步辐射X射线衍射图谱

图5 纳米晶Ni在常压和选定温度下的飞行时间中子射线衍射图谱

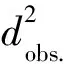
图6所示数据表明，观测到的原始数据(图6中黑色空心圆圈)呈现出显著的分散性，并且随着压力增加分散性增大.这种数据的分散性在微米晶Ni或其他微米尺度的陶瓷或矿物样品中并未被发现.由于数据点分散，不能通过简单的直线对其进行拟合进而得出应变和晶粒尺寸信息.由此，我们提出了一种基于不同晶面的杨氏模量的修正方法：

(3)

其中，S1和S2为弹性柔度数据.对于纳米Ni，我们根据衍射弹性比的平方(DER2)，提出了以下归一化路线，并选择柔度最小(hkl=111)或最大(hkl=200)的晶面作为参考：

DER2=(Ehkl/E111)2,

(4)

以及

DER2=(Ehkl/E200)2.

(5)

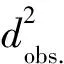
图6 纳米晶Ni中Δ/d2随d2(P,T)的变化趋势

2.3 纳米晶Ni的屈服与升压-卸压能量耗散

我们通过两组同步辐射X射线衍射实验在室温下同时研究了纳米晶和微米晶Ni的加载和卸载循环.在两次衍射实验的最大压力下(分别为1.4和6.0 GPa)，用公式(2)测定的纳米晶Ni的应变绝对值比微米晶Ni高3～4倍.为了便于比较，我们将实验得到的应变与在最高压力下的最大应变值进行了归一化，结果如图7所示.从图7中可以看出，微米晶Ni在Py1=0.4 GPa和Py2=1.6 GPa有两个明显的屈服点，对应的归一化应变量分别为εnorm=0.7和εnorm=1.0.第一个屈服点代表粉末在压缩过程中在晶粒接触位置的高应力集中处产生的“局部”屈服；第二个屈服点表示整个样品的“宏观”塑性变形，也是经典力学中“屈服”的真正含义.

相比之下，在纳米晶Ni中并没有观察到这两个屈服点，“局部”塑性变形阶段预计在远低于0.4 GPa的压力下发生，很难用我们目前使用的实验技术来确定.另一方面，纳米晶Ni在高应变下观察到了明显的加工硬化作用.根据最大压力的不同，纳米晶Ni在卸载时具有更大的应变回复率，约为83%～84%，而微米晶Ni仅为49%～52%.不可回复的应变可以由晶间(如弹性和塑性的各向异性)或晶内(如应力和位错密度的非均匀分布)机制引起.前期的研究(Budrovic et al.，2004)表明，纳米晶Ni在单轴拉伸作用下，位错密度可完全恢复.在我们的三轴压缩实验中，纳米晶Ni不可回复的部分源于晶粒之间(弹性和塑性的各向异性)的应变，而微米晶Ni的不可回复的部分源于晶粒内部(位错密度)的应变.

从图7中还可以看出，屈服后的样品(b)比屈服前的样品(a)具有更显著的加载-卸载迟滞回线，但两种样品在屈服前后的应变恢复率相当，表明Ni的位错密度在弹性加载阶段趋于饱和，在塑性变形阶段没有进一步增加.屈服后微米晶Ni的迟滞回线很大，说明高压对微米晶Ni的作用以热量的形式消散.相比之下，纳米晶Ni的迟滞回线很小，说明在加工硬化塑性变形阶段的能量损失明显降低.纳米晶Ni在加载-卸载循环过程中能量耗散水平的降低表明，纳米材料在循环加载中可以承受更大的机械疲劳，这是纳米力学的一个重要发现.

图7 加载(实线)和卸载(虚线)过程中纳米晶Ni(红线)和微米晶Ni(蓝线)的归一化表观应变随压力的变化曲线

纳米晶Ni在室温下升压和卸压时晶粒尺寸随压力的变化如图8所示.在压缩过程中，三个独立的实验显示，在屈服压力之前(即在～1.8 GPa以下的弹性变形阶段)，样品的晶粒尺寸减小或发生破碎.该现象在硬脆性陶瓷材料中也可以观察到(Qian et al.，2005)，其原因为高压会抑制原子扩散并提高样品黏度.当P=7.4 GPa时，即纳米晶Ni发生整体塑性屈服后，在室温下观察到了纳米晶Ni的晶粒长大了约60%.对于纳米晶Ni，压缩过程中在塑性屈服/黏性流动阶段的晶粒生长是由“冷焊”引起的.在较大的偏应力驱动下，晶粒间的原子扩散和晶格旋转会使“非择优取向”的纳米晶粒相连接，从而导致晶粒长大.我们的实验结果与Shan等(2004)的研究一致，他们认为纳米晶Ni在拉伸时发生的晶粒长大是由塑性变形时晶粒的旋转所导致.卸压后样品晶粒尺寸的变化与升压过程中观察到的趋势相似，当压力完全释放后，晶粒尺寸恢复到初始值.这种可逆性晶粒尺寸变化的原因尚不清楚，但可能与卸压过程中样品所经历的不同应力状态有关.

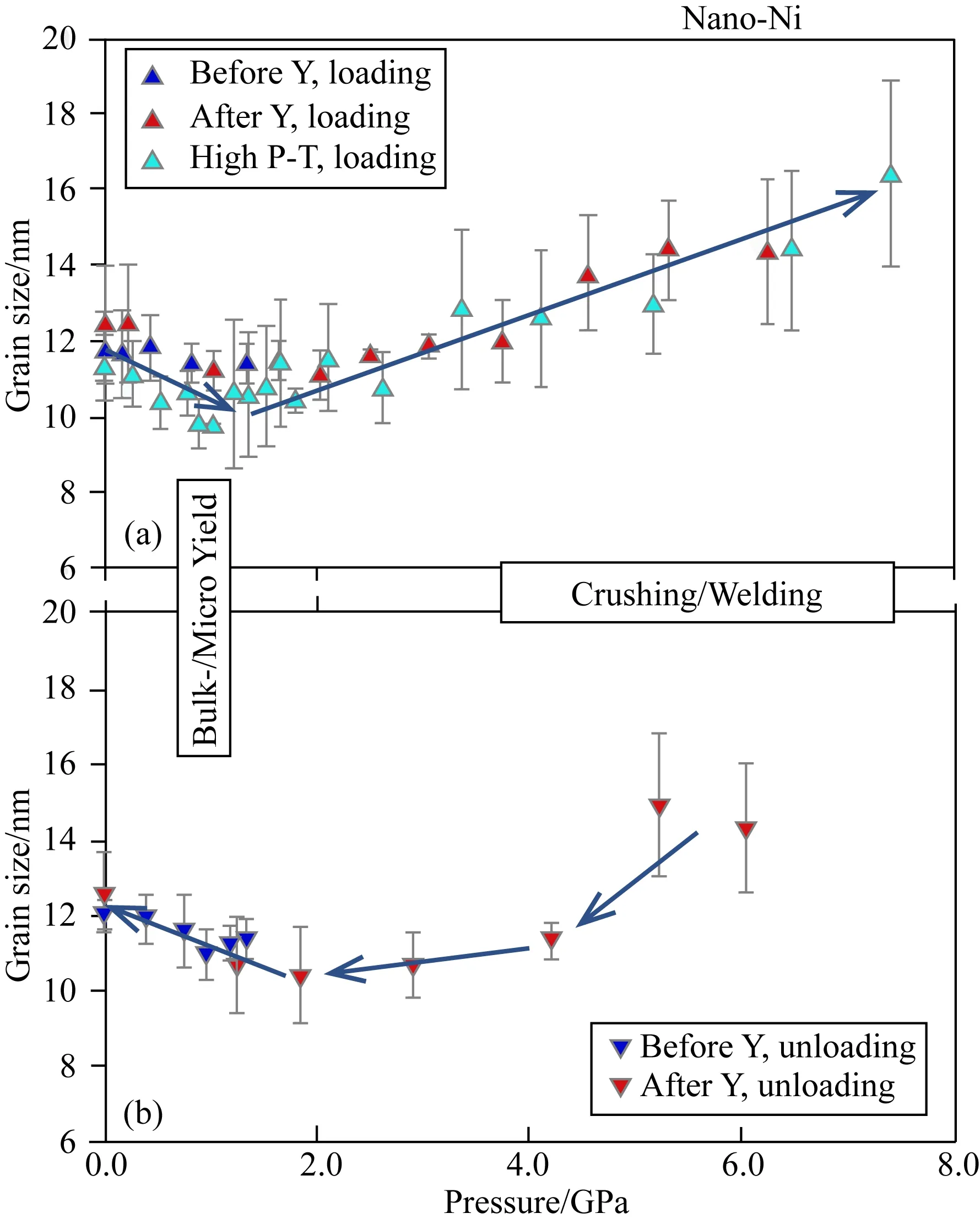
图8 纳米晶Ni在室温下(a)加压和(b)卸压过程中晶粒尺寸随压力的变化趋势

2.4 纳米晶Ni的高温高压应力分析

我们使用同步辐射X射线对微米和纳米晶Ni同时在高温高压条件下进行了对比实验，压力和温度的极值分别为7.4 GPa和1400 K.为了比较微米和纳米晶Ni的高温力学性能，根据实验结果将表观应力表示为压力和温度的函数，结果如图9所示.在计算时，首先利用衍射数据根据公式(2)计算出表观应变，然后通过σ=E·ε计算出表观应力.根据图2中的结果，纳米晶Ni比微米晶Ni的弹性模量减少了10%，因此在计算中纳米晶Ni和微米晶Ni的杨氏模量分别取E=180 GPa和E=200 GPa.尽管该数值忽略了压力和温度对弹性模量的影响，但并不会对整体的变化趋势产生影响.

纳米晶和微米晶Ni的初始应力差是由残余应力、表面应变和晶粒尺寸效应造成的.随着压力的增加，在弹塑性过渡区，即从“微观/局部”屈服到“宏观/整体”屈服阶段，纳米晶Ni的晶粒间的接触应力以更大的速率增加.当整个样品的强度小于偏应力或剪切应力时，即开始发生宏观/整体屈服，并伴随着塑性变形或黏性流动的开始.相应的，在发生宏观屈服后衍射峰宽度变化不大，说明样品中的位错密度达到了饱和.

图9 纳米晶和微米晶Ni的表观应力随着压力和温度的变化曲线，其中包含了微观应变和仪器影响.“屈服”点为弹性加载阶段和塑性加工硬化/软化阶段的交点.两种样品显示出了不同的初始屈服压力

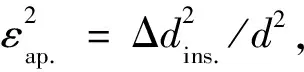
在所有实验温度下，用公式(2)得到的晶粒尺寸如图10所示.当温度小于573 K时，纳米晶Ni没有发生晶粒长大现象；在573～773 K温度范围内，经E200和E111修正后，晶粒尺寸分别从13.5 nm增长到36.8 nm和从18.1 nm增长到49.3 nm；温度大于823 K时，晶粒迅速长大并接近微米尺度.图10还给出了压力为7.4 GPa时晶粒尺寸随温度的变化规律.当温度小于573 K时，晶粒尺寸基本保持不变；当温度继续升高时，晶粒的长大速率与常压相比明显减小.这些结果表明，压力是控制结晶过程的一个有效的热力学参数.由于晶粒生长通常伴随着长程原子重排，它在高压下在动力学上将受到阻碍或抑制.因此，压力也是合成纳米结构陶瓷材料的关键控制参数(Zhao et al.，2004).

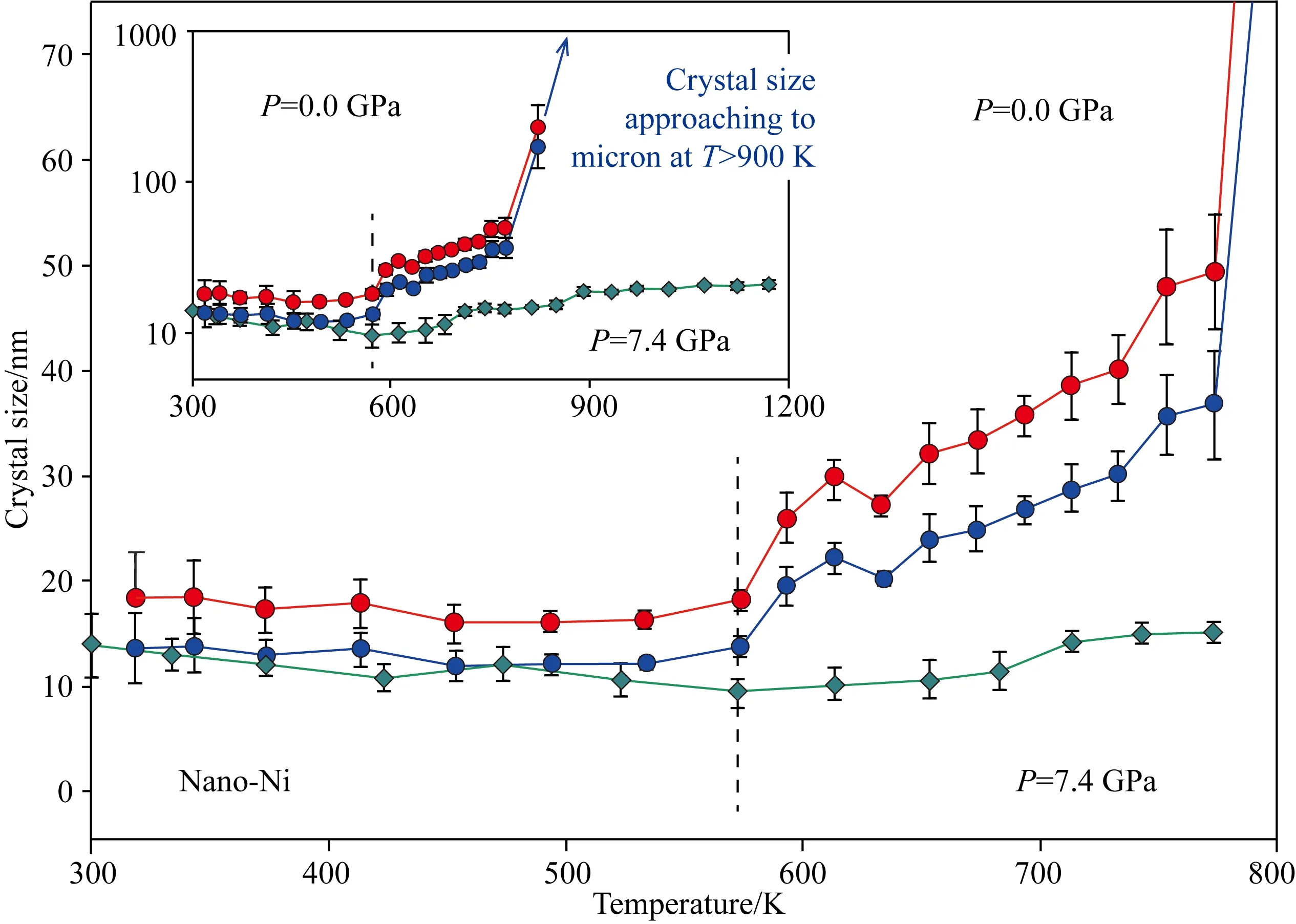
图10 纳米晶Ni在常压(中子衍射数据)和7.4 GPa(X射线衍射数据)下晶粒尺寸随温度的变化曲线.所有数据均由公式(2)计算得出并代表纳米晶Ni的平均晶粒尺寸

2.5 纳米晶Ni中的位错密度

为了得出纳米晶Ni中位错密度ρ随退火温度的变化规律，我们利用中子衍射数据结合以下公式进行计算(Shen et al.，1995)：

(6)

其中，b为位错伯氏矢量的绝对值，A为常数，取值为3.3(Révész et al.，1996)，C是取决于材料的弹性各向异性的对比系数，可以通过C44/(C11-C12)和C12/C44来表征，其中C11、C12和C44为弹性常数.公式(6)中的所有其他参数与公式(2)中的含义相同.

由公式(6)得到的位错密度和晶粒尺寸随退火温度的变化趋势如图11所示.对比图10和图11中可知，由公式(2)和公式(6)所得到的晶粒尺寸的绝对值以及随温度的变化趋势是一致的.初始纳米晶Ni的位错密度约为0.053 nm-2，当温度为573 K时，位错密度约为0.019 nm-2，减小了约三分之一.当温度在573～873 K范围内时，随着温度的升高，位错密度不断减小，晶粒尺寸不断增大.

图11 纳米晶Ni的位错密度ρ和晶粒尺寸L随温度的变化关系

Ashby(1970)认为，晶体在塑性变形中产生的位错可以分为“几何必需”位错(与晶界的存在相关的位错)和“统计存储”位错(参与塑性变形的滑移位错).在图11中，存在一个晶粒尺寸保持不变但位错总密度显著下降的温度范围.晶粒尺寸恒定表明在该退火温度范围内“几何必需”位错的密度没有发生改变，而实验观察到的总位错密度的下降是由于球磨过程中“统计存储”位错的湮灭所导致的.在较高的退火温度下，晶粒尺寸增大是由几何必需位错密度减小造成的.显然，这两种不同类型的位错在纳米晶Ni中都与晶粒尺寸的变化有关.

3 结论

通过高温高压下的同步辐射X射线衍射和飞行时间中子衍射实验，我们提出了一种利用衍射数据研究和分析纳米晶本征力学性能的方法.利用该方法研究了纳米晶的弹性软化、微观应变、屈服强度、位错密度以及高温下的力学性能等.结果表明，在纳米晶Ni中存在明显的弹性软化现象，并证实了纳米Ni具有张性壳层.根据衍射数据的峰形分析得到了纳米晶Ni的屈服强度为2.35 GPa，是微米晶Ni的3倍以上；与单轴拉伸实验相反，纳米晶Ni在高压塑性变形阶段表现出明显的加工硬化，而微米晶Ni则在高压下表现出了一定的加工软化，并有较大的能量耗散.加载-卸载循环过程中的迟滞回线表明，纳米晶Ni的能量耗散比微米晶Ni显著降低，说明纳米材料在循环加载过程中能够承受更大的机械疲劳.纳米Ni在弹性变形阶段表现出了晶粒破碎现象，而在高压加载下的整体塑性变形过程中晶粒稳定生长.在高温退火过程中，随着温度的升高，纳米Ni在573 K以上出现了明显的应力降低和晶粒长大现象.在高温下，7.4 GPa下的晶粒生长速率明显小于常压下的晶粒生长速率，表明压力是控制晶化过程的有效参数.对纳米Ni中的位错密度进行计算的结果表明，晶粒尺寸随温度和压力的变化与“几何必需”位错和“统计存储”位错都具有相关性.本文使用的方法可以定量测定岩石矿物的高温高压流变强度，为反映大陆中上地壳的真实流变结构情况及发生在中上地壳的地震及其余震深度分布规律探索提供新的研究方法，为研究岩石圈以及地幔物质的蠕变对流提供了高科技的研究手段.