基于摄影测量的数字化测量工程基坑变形观测系统设计

牛 冲

(山东省地质测绘院, 山东 济南 250013)

0 引言

随着建筑工程不断地开发,建筑工程开展频繁,而深基坑工程中,当基坑出现变形情况未被发现时,容易造成倒塌损耗,对工程安全造成影响[1-3]。而对基坑变形的监测,早期采用人工测量的方法,但随着工程规模不断加大,人工测量会浪费大量人工成本,同时监测效率较低[4-6]。因此研究者们开始向着数字化测量方向进行研究。而在目前的研究中,使用较多的方法是利用全球导航卫星系统(Global Navigation Satellite System,GNSS)技术,对基坑周围的结构顶点进行检测,并获取检测数据。但该方法对基坑边缘的监测效果不佳,同时精度较低。而数字摄影测量技术的应用不断扩展,利用摄影设备对物品的变形进行实时监测,经常实时性较好,同时获取的监测数据较为准确,具备未来的应用发展前景,可以尝试在工程基坑变形的观测中进行应用。

1 基于摄影测量的数字化测量工程基坑变形观测系统软件设计

在摄影测量的基坑变形观测系统中,相应的摄影测量设备需要根据工程参数的不同进行选择,因此，在本文设计中,重点在观测系统的软件设计。

1.1 摄影测量成像模型

在摄影测量领域中,理想的摄影成像应该属于针孔投影,通过被测物体的反射光,经过一个针孔投影至相机成像面中[7-8]。如图1所示。

图1 相机成像针孔模型

在图1中Oc代表相机的投影中心,Xc轴与Yc轴与X轴与Y轴相互平行,Zc轴则做为相机的主光轴,同时和图像平面处于垂直状态。Zc轴和成像对应面的角点则作为模型原点,并通过Oc-XcYcZc形成空间坐标系,则可以得出被测物体P在空间坐标和平面坐标内的关系

(1)

并根据齐次坐标来表示其中的投影关系,得出

(2)

而图像在计算机中呈现时,数字图像以M×N的数组的形式来进行表示,每个单一数组代表一个像素,在本文系统中,成像出的图像是由M行和N列的像素形成,如图2所示。

图2 成像坐标和图像坐标关系

在图2中,通过u轴和v轴共同组成的直角坐标系,原点坐标为(u0,v0)，作为该图像的图像坐标系,并以像素为单位,而像素的点坐标(uq,vq)代表像点q在坐标系中的坐标,而其中q则可以代表改图像像素点所在的行位置和列位置。根据上述方法将相机中获取的图像更好地进行成像。

1.2 基坑变形检测数据处理

本文利用了摄影测量技术对基坑变形进行监测,可以将基坑变形中的运动用一组地面点和空间点来进行表示。由于基坑运动中获取的数据存在动态噪音,本文利用科尔曼滤波法对数据进行处理。将这些点看作时间t的函数,高程监测网则作为运动的一维网格,而基坑的平面监测网则可以作为二维网格。为了对被测基坑的变形情况进行检测,本文将点位置和运动速率作为状态向量,并设点i在时刻t中的位置向量为εi(t),将瞬时速率设为λi(t),在通常情况下,则存在一定的随机干扰,设Ωi(t)代表动态噪音,得出微分式

(3)

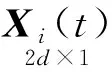
(4)

在(4)公式中,d代表对应监测网的维数；q代表监测网的待定点数之和,则可以推导出离散化状态方程

(5)

1.3 基坑变形值数据计算

将上述滤波控制后的图像数据进行变形值计算。考虑到实际使用中,往往测量摄影设备环境不良,摄影设备的内、外方位元素初始值难以得到[9-10]。因此，本文利用时间基线法对基坑的变形情况进行测定。通过选定的固定摄影点,在摄影中将摄影设备的成像平面与基坑平面平行。并以一定的时间间隔,进行像片拍摄,并将目标中的起始位置和摄影成像中所有点位在一定的时间间隔下,平行与成像平面中的点位的相对位移量,并得出差异值。当被测基坑点上的某点位移A变形成B,那么得出在X轴和Z轴上的位移变形量,ΔX和ΔZ则为

(6)

式(6)中,PX和PZ分别代表图像在X轴和Z轴上的差异值;M则代表图像比例系数;f代表摄像设备的焦距。由于在实际作业中容易出现摄像机的内、外方位元素无法测得的情况,因此，在其中增加直接线性变换解法,对图像中的变形点进行三维坐标变化求解。首先根据精度要求来设置对应的限制,并根据正算误差方程得出图像中的已知条件L,方程公式为

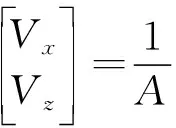
(7)

在进行正算后,可以利用反算的误差方程,设正算中解出的L系数为已知条件,并根据立体图像对变形点进行物方空间坐标Xu,Yu,Zu求解,得出

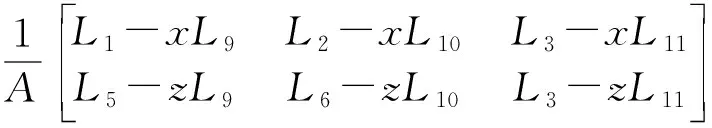
(8)

式(7)、(8)中，X、Y、Z分别为空间坐标系中的三维坐标，x、z分别为图像上对应三维点的像素坐标，在进行正算后，Li为笛卡尔空间坐标系与像素坐标系之间的关系系数。将获得的物方坐标和式(6)中结果相减,即可获得三维变化值。需要注意的是,在实际使用该方法时,需要将物方坐标系的原点选定在被测点范围内,并使A=1的数值与解求值相近,保证循环趋近解算可以实现快速的收敛。

2 实例论证分析

为了验证设计的基坑变形观测系统的可用性,本文对某一项目工程进行基坑观测,通过对该工程中的基坑变形观测结果来判断设计系统的可用性。

2.1 工程介绍

本实验应用的实例建筑工程中,总建筑面积达到103 062.2 m2,在该建筑工程中地下室面积达到33 451.21 m2。在修建中,规划的基坑形状为四边形,基坑内的支护边线根据该工程的地下室建设的承台外边线扩展760 mm,并根据规划的开挖内边线来进行计算,场地周长约在790 m左右,场地面积达到31 821 m2。而在基坑的建造中,场地的地面高程根据国家基准选取为3.00 m。集成采用桩基承载台,并对基坑内A1～A7选用PHC-500型管桩。本工程中基坑规划挖深为5.74 m,底板面标高度为-4.00 m,设计用的桩基板厚度为360 mm,工程在桩板下另外设置110 mm厚的C14素混凝土垫层。根据工程环境,本工程的基坑安全等级为三级,坑中深坑安全等级为二级。

2.2 工程区域土层分布

对基坑来说,地区土层情况对基坑的变形会存在较强的影响,而该工程进行先行探测,得出的地区局部土层分布如图3所示。

图3 局部土层分布情况

图3中,第①号土层主要为素填土,颜色呈灰黄色,为人工堆积土层,且堆积年代低于3年,分布较为均匀。第②号土层为淤泥质填土,颜色呈灰黑色,其中含有一定的生活垃圾,厚度分布不均。第③号土层主要为黏土,颜色呈褐灰色,压缩性和韧性均较为中等,同时局部的粉质含量较高,结构紧密。第④号土层为粉质黏土,颜色呈灰黄色,粉质含量较高,工程性质较为一般。第⑤号土层为粉土夹粉质黏土,颜色呈灰色,强度韧性均较低。地下土层的参数如表1所示。

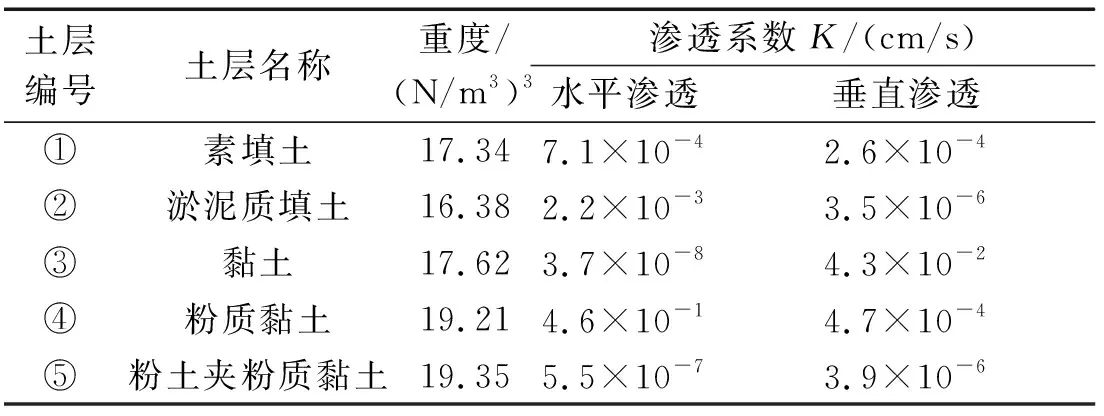
表1 基坑局部土层泥土性能参数

2.3 观测点分布

在本项目的施工现场上,采用本文设计的基坑变形观测系统进行基坑观测,对该工程上,设置了7个观测点,分别为C1～C7,分别处于基坑的不同位置,以保证观测结果的准确性,观测点分布情况如图4所示。

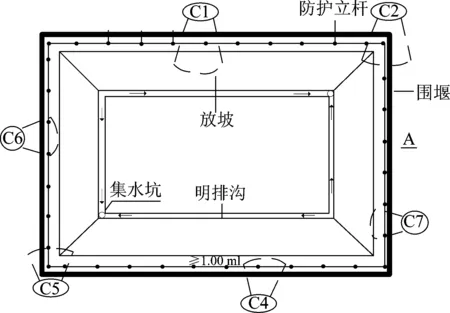
图4 基坑观测点分布图

考虑到对该基坑的施工共分为基坑开挖,地下室开挖,土方回填,而在不同工程环节下施工时间不同,同时对基坑的边坡受力影响也不相同。因此，对该工程的观测主要是针对三次工程环境间基坑的变化,以及工程过程的定期变形监控。

2.4 观测数据结果

在对该工程进行基坑变形观测中,对每个环境均进行了9次观测,由于观测数据结果较多,本文选取每个工程环境中第2次的观测结果,在进行基坑开挖时基坑变形观测第1次观测结果如表2所示。

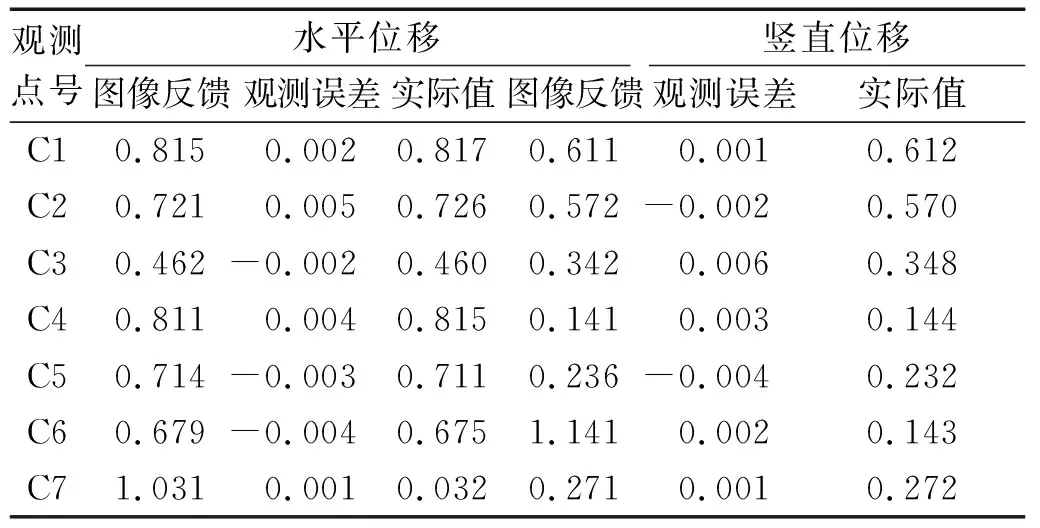
表2 基坑开挖时第2次观测数据表 单位：mm

在表2中可以看出,该工程在基坑开挖时,出现了一定程度的基坑变形,但变形幅度较小。也可看出,本文设计的基坑观测系统可以有效地对基坑变形数据进行获取,且误差值较小。该工程再进行地下室开挖时基坑变形观测时的第2次观测数据如表3所示。

表3 地下室开挖时第2次观测数据表 单位：mm

表3中的反馈参数位移变化是上一次的观测结果为基准得出的反馈参数,而在表2中本文观测系统的观测误差值也在较小的范围内。对该工程在土方回填环境中的第2次观测数据如表4所示。

表4 土方回填时第2次观测数据表 单位：mm

从表2、3、4中的观测数据均可看出,本文系统的观测误差较低。为了更直观验证观测结果的误差，本文将在土方回填时的C1观测点获得的数据和实际结果进行对比,如图5所示。

图5 土方回填时C1位置的水平位移对比图

通过数据统计可以看出,本文设计的基坑变形观测系统,观测结果具有较高的精度从图5可以看出,观测到的位置数值与实际的位移数值相差很小,证明具备较高的观测精确度。并且可以实现水平和竖直的位移观测,系统具有可行性。

3 结束语

本文通过使用摄影测量技术,设计了数字化测量工程基坑变形观测系统,同时在实际的项目应用中的结果也证明了该系统具有较好的观测性能和实际应用能力。但在实际应用中,工程期间并未出现较为恶劣天气,因此，对本文系统在恶劣天气下的观测能力无法进行检验。同时系统目前仅能实现对变形的观测,无法得出相应的未来变形预测,未来考虑利用遗传算法对得出的变形数据进行计算,来实现变形预测。