整体式箱形截面梁静力荷载试验空间效应的精细化有限元分析

李杨梅

（宁夏交投高速公路管理有限公司，宁夏 银川 750000）

箱形截面梁由于其良好的结构性能，在现代梁桥中得到了广泛的应用[1]。但由于在恒载和活载的双重作用下，外部作用综合表达为非对称的偏心荷载，如需要得到相对精确解，则应在结构静力分析时考虑偏载效应以及剪力滞效应叠加后的空间效应影响。钟新谷等[2]较早采对箱梁进行精细化分析，分别采用顶板、底板、腹板、横隔板等多种元件单独建立的刚度矩阵进行箱梁空间非线性分析。常诚[3]采用实体单元对全国六千余座混凝土现浇箱梁的偏心增大系数进行计算，发现箱梁宽跨比越大，偏心增大系数越大，并初步将简支箱梁的偏心增大系数定义在1.15～1.5 之间。

经过大量检验，采用空间实体模型进行变形和应力分析是精确而有效的[4]，但是我们并不能够对所有结构物的计算均采用此种相对费时费力的方法。由于没有清晰的界定，工程人员仍然以简化了的梁单元模型计算为主，辅以偏载系数和翼缘有效宽度来包络住偏载效应和剪力滞效应的影响，这对于静力荷载试验检测来说，尤其是对于宽箱截面箱梁存在明显误差。各测点理论计算值相对准确，才能对荷载试验结果进行准确的判断。

1 箱梁空间效应简述

1.1 纯弯梁理论

纯弯梁理论假定在纯弯曲荷载下梁截面符合平截面假定，即梁截面在变形前后都保持在同一平面，弯曲正应力（σx）按式（1）计算，其中，My为梁截面弯矩，I 为梁截面抗弯惯性矩。

1.2 偏载效应

箱梁在偏载作用下的变形和位移包括纵向弯曲、横向挠曲、扭转和畸变[5]。通常采用梁单元模型进行计算分析时，分析结果只包括了纵向弯曲和自由扭转引起的变形和位移，而不包括横向挠曲、约束扭转和畸变的影响，因此根据设计习惯引入偏载系数（一般是取1.15）对活载效应进行修正。但是不同年代处理方式并不一致，对于近些年保存完好且作业规范的桥梁，设计说明里一般会体现整体计算思路及计算考虑，但是对于年代较久远的桥梁很多设计信息是缺失的，凭经验引入的偏载系数可能与原设计并不一致[6，7]。并且仅采用梁单元进行简化计算，也不能够得到荷载作用下梁截面横向的真实应力和位移分布。

1.3 剪力滞效应

一般来说，箱梁腹板间距不大时，可采用纯弯梁理论计算应力分布，当腹板间距较大时，还需要计入“剪力滞效应”，这种在同一纤维层上沿翼缘宽度变化的法向应力，需用高等材料力学方法求解[8]。在结构计算分析中为了包络掉剪力滞效应所带来的影响，同时方便的应用初等材料力学方法求解，一般是采取考虑翼缘有效宽度的做法。

1.4 梁单元和实体单元各自包含的计算内容对比

综合前文分析可知，为更准确计算分析箱梁静力性能，需在有限元建模过程中综合考虑偏载效应和剪力滞效应等的影响，而实体有限元方式可以更方面考虑上述影响。

2 不同宽跨比下梁单元与实体单元计算结果分析

本文基于加载横向布置及纵向布置按静载试验常规做法，加载示意图见图1-2。基于既有文献研究结果，建立了1:1～1:5共5 种宽跨比的纯弯梁单元模型与实体单元模型。

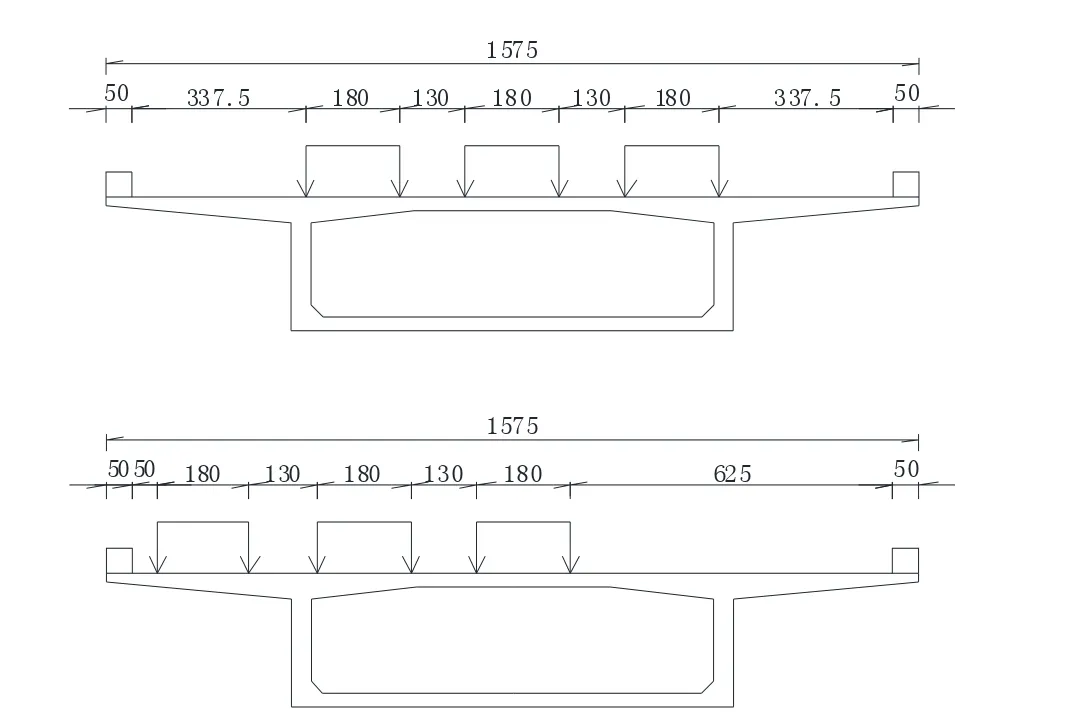
图1 对称加载和偏心加载载位横向布置示意图（单位：cm）

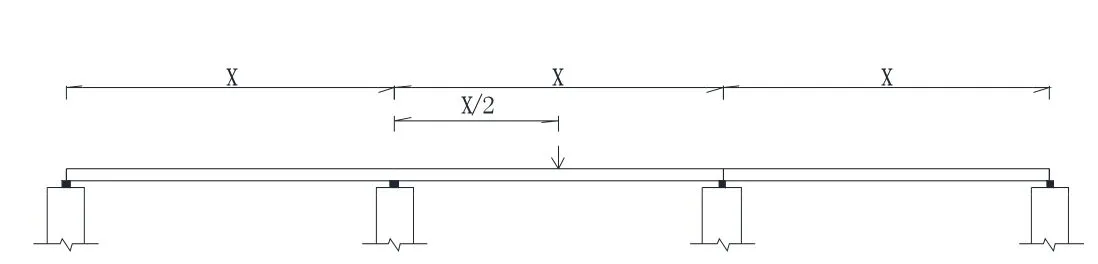
图2 对称加载和偏心加载载位纵向布置示意图（单位：cm）

2.1 对称加载

中跨跨中截面在对称加载作用下，荷载试验主要测试项（应变和位移）的理论计算偏差如表1 所示。表内数字为梁单元计算结果（梁单元偏载理论值考虑了1.15 的偏载系数，并进行了内插计算）与实体有限元计算结果之比。基于表2 计算结果得到的对比分析如图5 和图6 所示。

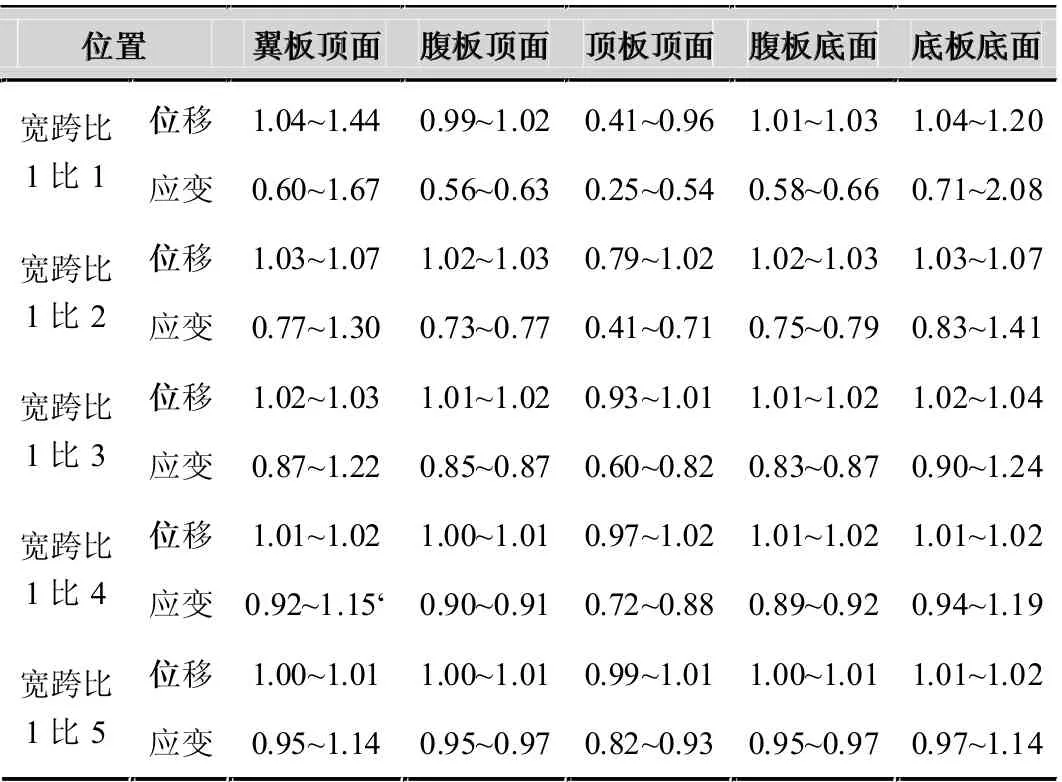
表1 不同宽跨比对称加载作用下梁单元与实体单元结果之比汇总表

从表1 和图3、图4 可以看出：

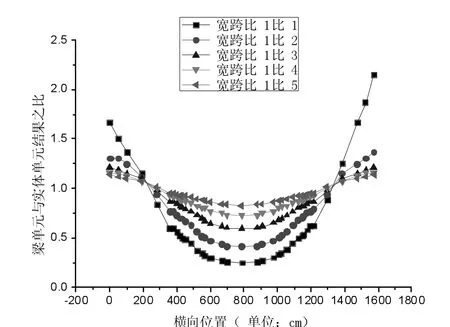
图3 对称加载顶板位移及应变分布

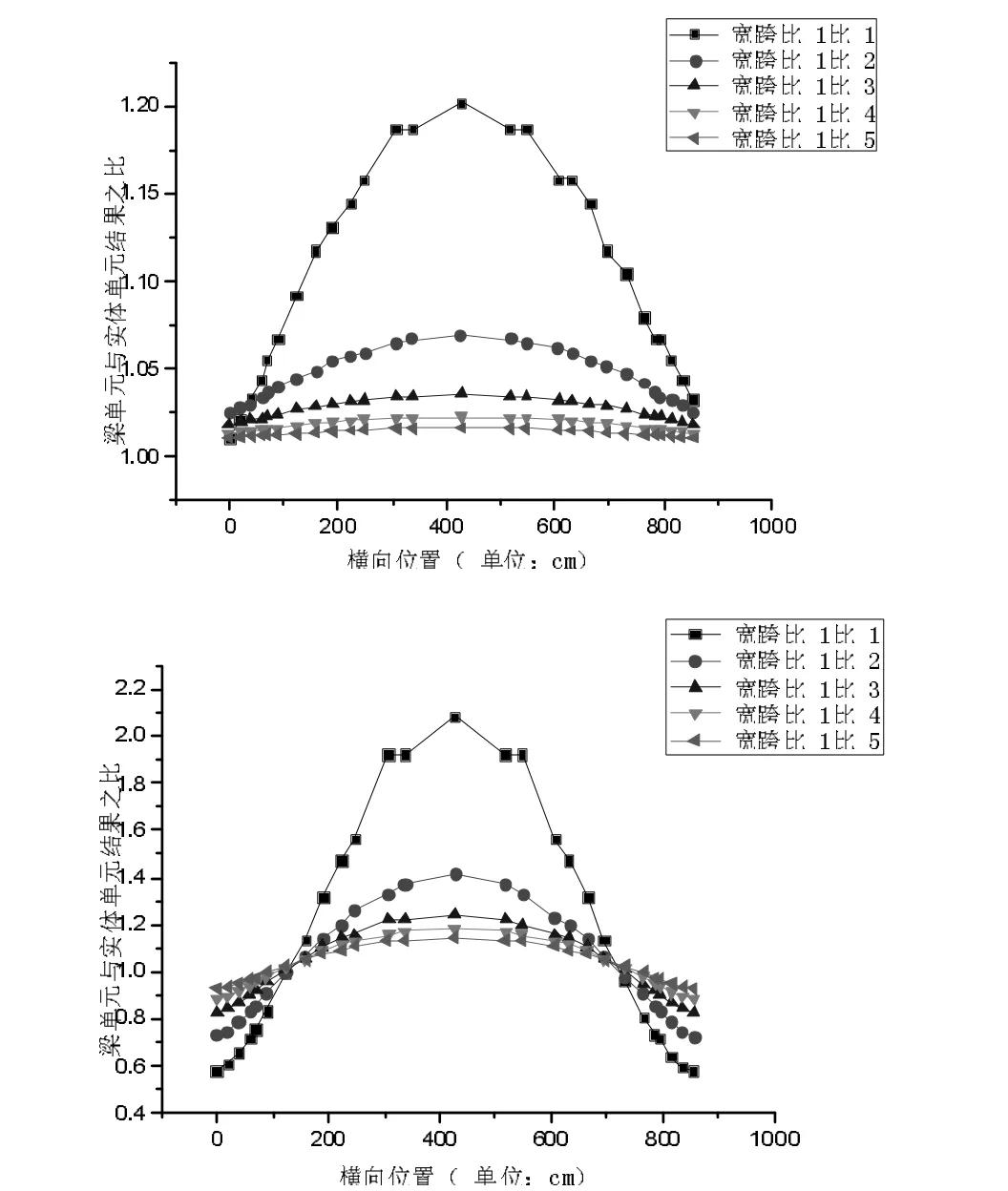
图4 对称加载底板位移及应变分布

（1）对称加载作用下，对于整体式箱梁截面，简化模型与精细化模型各点位理论计算值随着宽跨比的减小，呈逐渐接近的趋势。

（2）宽跨比为1：3 时，顶板中心处的各别点位梁单元与实体单元位移计算偏差在7%左右，其他点位偏差均在5%的工程误差以内，梁单元的位移解是可以使用的，应变解计算偏差仍然较大，不推荐使用。

（3）宽跨比为1：5 时，翼板最远端以及顶板中心处附近的各别点位梁单元和实体单元的应辩解计算偏差在15%左右，其他点位偏差均在5%的工程误差以内，梁单元的位移解和应变解是可以使用的。

2.2 偏心加载

中跨跨中截面在偏心加载作用下，荷载试验测试应变和位移的理论计算偏差如表2 所示。表内数字为梁单元计算结果（梁单元偏载理论值考虑了1.15 的偏载系数，并进行了内插计算）与实体有限元计算结果之比。对比分析如图5 和图6 所示。

从表2 和图5、图6 可以直观看出：

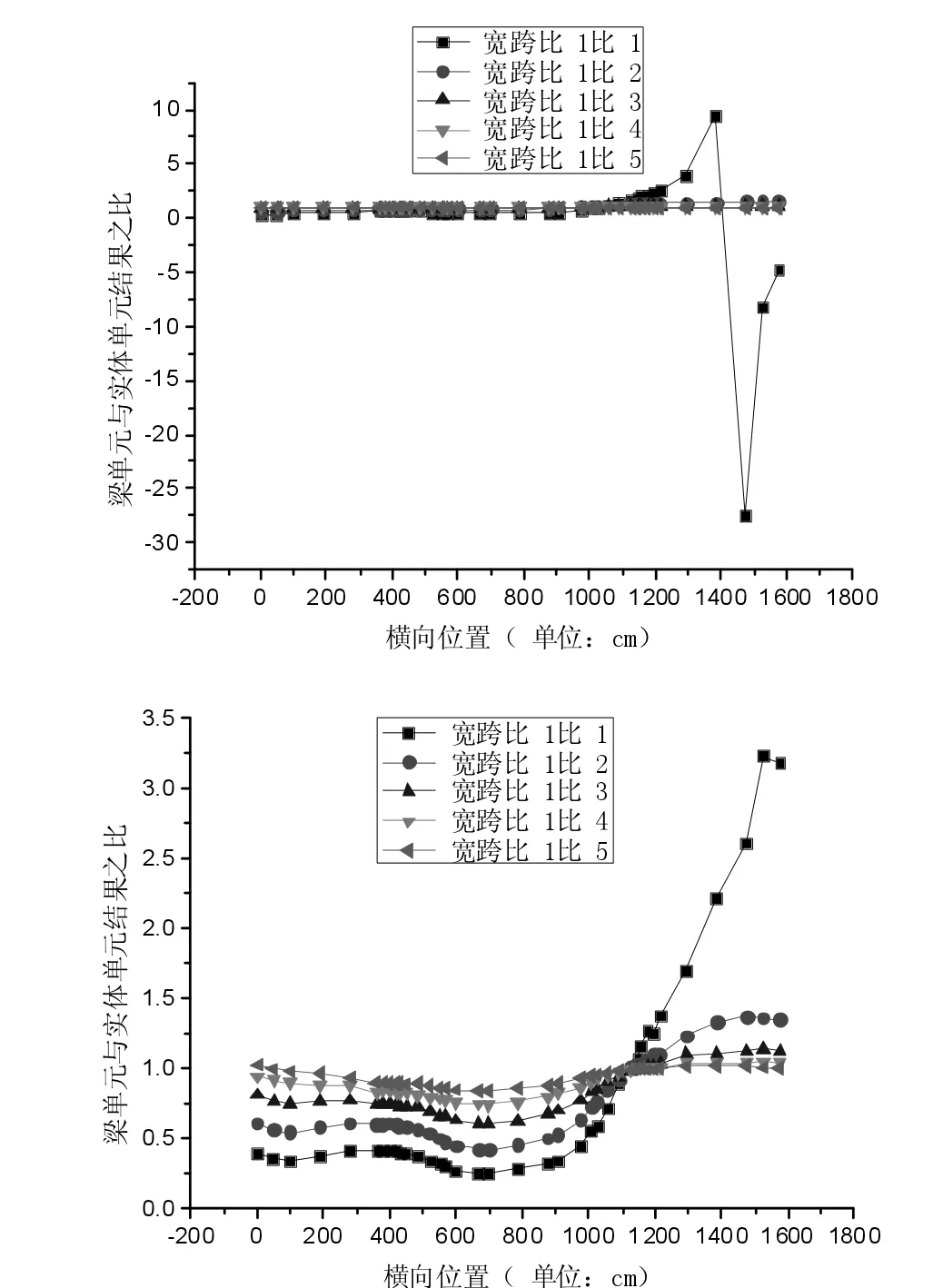
图5 偏心加载顶板位移及应变对比结果分布

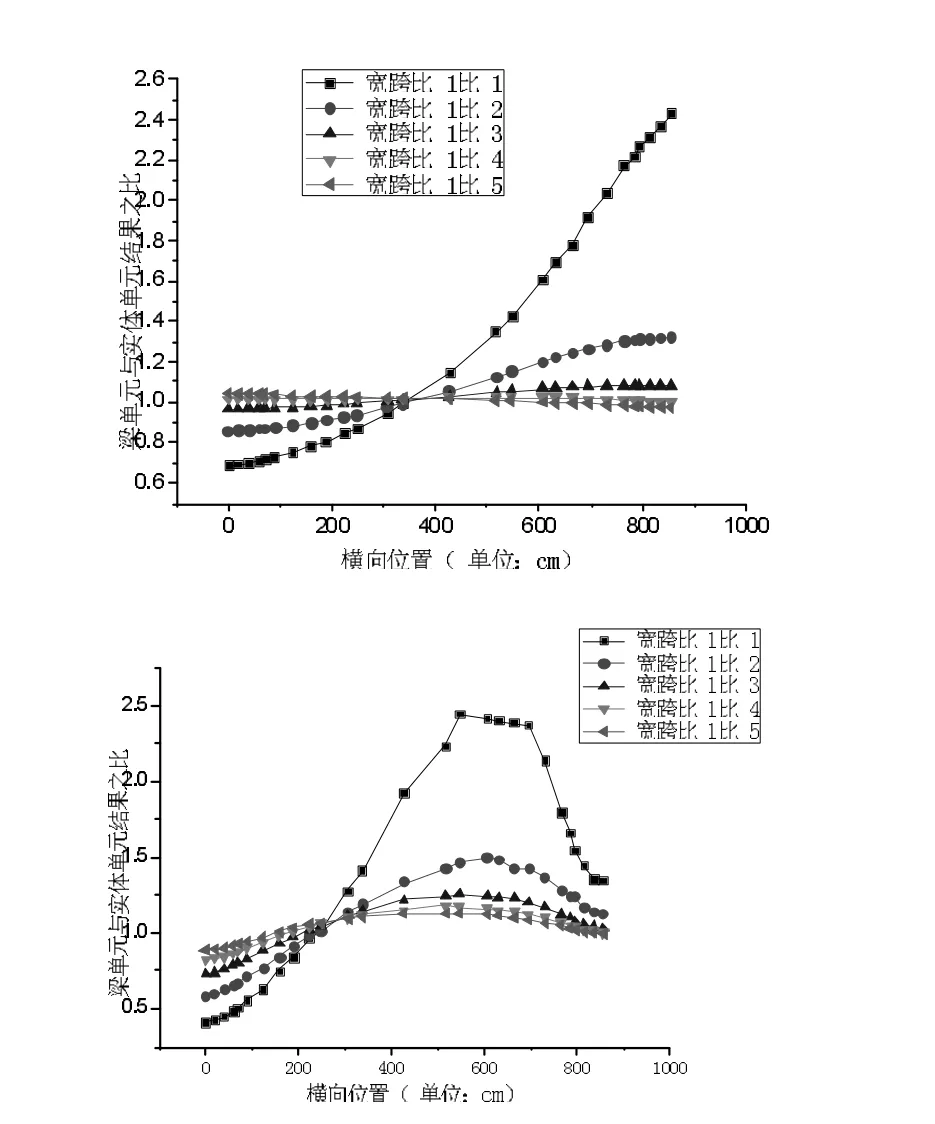
图6 偏心加载底板位移及应变对比结果分布

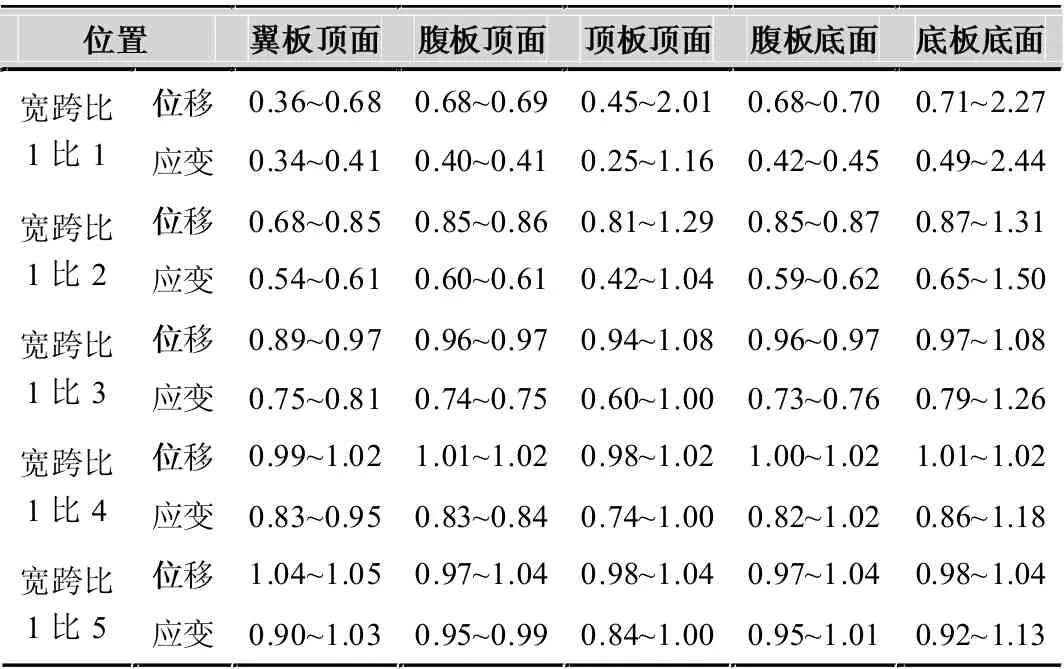
表2 不同宽跨比偏心加载作用下梁单元与实体单元结果之比汇总表

（1）偏心加载作用下，对于整体式箱梁截面，简化模型与精细化模型各点位理论计算值随着宽跨比的减小，呈逐渐接近的趋势。

（2）宽跨比为1 比3 时，顶板中心处的各别点位梁单元与实体单元位移计算偏差在10%左右，其他点位偏差均在5%的工程误差以内，梁单元的位移解是可以使用的，应变解计算偏差仍然较大，不推荐使用。

（3）宽跨比为1 比5 时，翼板最远端以及顶板中心处附近的各别点位梁单元和实体单元的应变解计算偏差在15%左右，其他点位偏差均在5%的工程误差以内，梁单元的位移解和应变解是可以使用的。

3 结论

本文通过采用简化梁单元和实体梁单元对不同宽跨比箱梁进行计算分析，发现精细化模型能够更好反映箱梁静力行为的空间效应。通过对比，进一步验证了实体单元对箱梁静力行为模拟的准确性。具体结论如下：

3.1 对于整体式箱梁截面，随着宽跨比的减小，简化模型与精细化模型各点位理论计算值呈逐渐接近的趋势。

3.2 宽跨比为1：3 时，翼板最远端以及顶板中心处附近的个别点位梁单元与实体单元位移计算偏差在10%左右，其他点位偏差均在5%的工程误差以内，梁单元的位移解是可以使用的，但应变解计算偏差仍然较大，因此不推荐使用。

3.3 宽跨比为1：5 时，翼板最远端以及顶板中心处附近的各别点位梁单元和实体单元的应变解计算偏差在15%左右，其他点位偏差均在5%的工程误差以内，梁单元的位移解和应变解是可以使用的。

此外，因空间效应考虑不足而造成的试验结果误判会带来两方面的影响。其一，不满足要求时误判为满足要求，结构在低承载能力水平运行，存在安全隐患；其二，满足要求时误判为不满足要求，随之而来的结果将是过度加固，养护经费的无效投入。虽然目前还不容易实现对所有的桥梁结构均采用空间实体单元进行仿真计算，但是，针对宽跨比小于1/5 时，尤其对于宽箱截面，在静力荷载试验主要测点校验系数为0.95～1.05 之间时（必要时可以将此系数范围扩大），建议应采用实体单元进行复核计算。