基于Dijkstra算法的地下物流配送路径优化研究
周冰 卢贝
摘 要:电商产业的崛起带动了物流行业的发展,虽然如今的物流行业已有了质的提升,但由此带来的问题也日益凸显,路上的车辆越来越多,越来越拥堵。地下物流系统的发展能有效解决此类问题,同时也符合社会可持续发展的需求。该文主要使用Dijkstra算法,对物流配送路径及节点的选择进行建模分析,求解出配送结点至各需求点的最短路径及所经结点,针对物流节点的选择提供一种行之有效的解决方法。
关键词:城市地下物流;最短路径算法;Dijkstra
中图分类号:TP391;F252 文献标识码:A 文章编号:2096-4706(2021)06-0091-05
Research on Underground Logistics Distribution Path Optimization Based on Dijkstra Algorithm
ZHOU Bing,LU Bei
(School of Information Engineering,Jiaozuo University,Jiaozuo 454000,China)
Abstract:The rise of E-commerce industry has led to the rapid development of logistics industry. Although todays logistics industry has been improved in quality,but the resulting problems are also increasingly prominent. More and more vehicles appears on the road,more and more congestion. The development of underground logistics system can solve such problems effectively. At the same time it also meets the need of social sustainable development. This paper mainly uses Dijkstra algorithm to model and analyze the choice of logistics distribution path and node,and solves the shortest path and the nodes passed by from distribution node to each demand point. It provides an effective solution for the selection of logistics nodes.
Keywords:urban underground logistics;shortest path algorithm;Dijkstra
0 引 言
本文依托“新型智慧城市建设背景下新一代物流体系的研究与应用”项目,基于对城市未来发展的展望和预测,构建新一代智慧物流系统的架构和体系仿真运行模型,研究地下物流节点选取及配送路径优化。地下物流系统是新一代的智慧物流系统,它是将地面物流系统与地下物流系统整合,形成一种更高效、更环保、更节省物理资源的物流系统。发展地下物流系统,能有效地缓解城市交通的擁堵,实现城市的可持续发展。将城市地下物流系统从网络层级上分为二级网络,并从二级配送节点出发,将货物至需求点所经过的路径及节点的选择进行了建模分析,通过求解,得到二级配送节点到覆盖范围内每个需求点的最短路径及所经节点。
1 地下物流系统整体设计
要加强数字化、信息化的建设,整体规划物流信息管理系统。对每一个物流中心、每一个配送节点、每一个转运点进行统一标准格式的编码,便于货物的流转(包括节点的选取和路径的选择)。对物流中心、配送节点、转运点的编码要有明显的字段,标识节点的不同类型,对于不同的省市区的节点进行编码也要有标识字段用于区分。此外还要大力推动“一单、一码、一单元”[1],避免如今“四通一达”、菜鸟、顺丰、京东、极兔等物流各自为战,各自都有一套自己的物流系统,信息交流不通畅,导致重复建设,资源浪费。
将每一个标准的物流包裹统一规划为物流单元,每个物流单元都会被分配一个唯一的“数字身份证”,也就是一码。每个物流单元都会被分配一个标准的电子货单(数字通行证),也就是一单,实现物流与信息流的融合,形成数字化物流网络。
整个城市地下物流系统的硬件组成部分,主要包括具体的物流中心、配送节点,支撑系统运行的自动分拣系统、存储系统、集散系统等,以及地下物流管道、社区配送装置等。
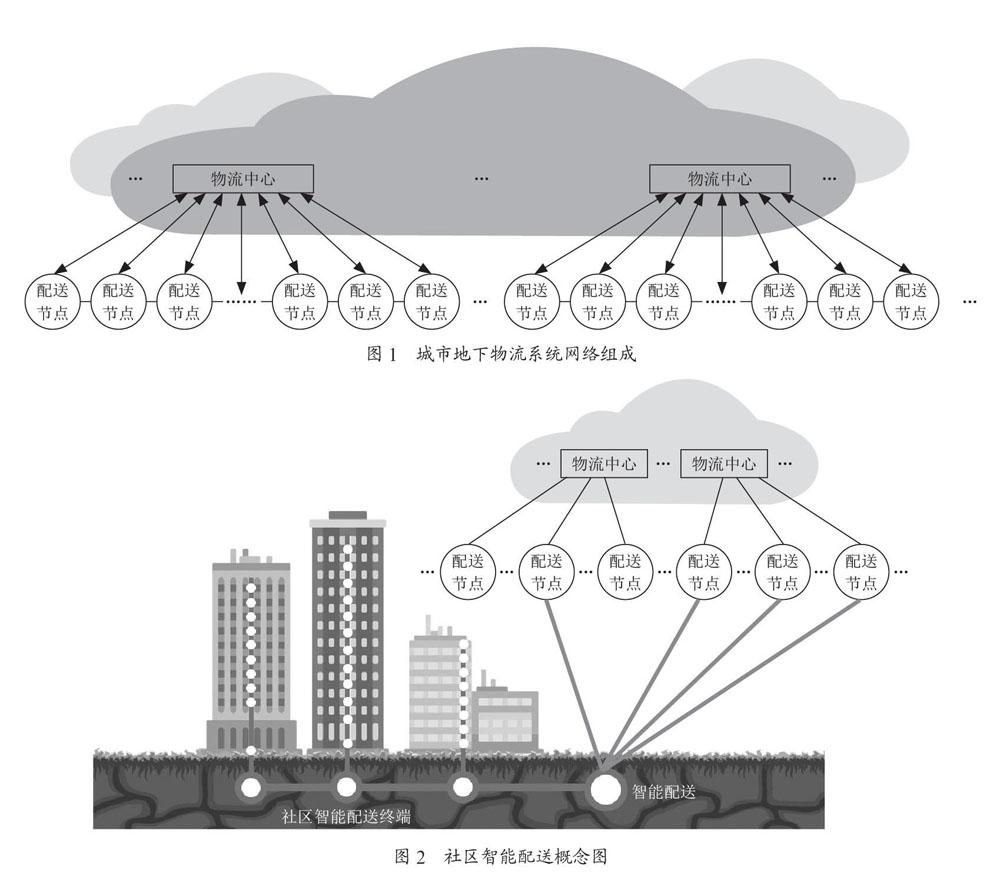
城市地下物流系统从网络层级上划分,可分为两级,一级为物流中心,二级为配送结点。两组一样的层级划分,每级之间都可进行关联转运,如图1所示。
第一级为物流中心。规模庞大,负责各种包裹的分发转运。该物流中心可与其他城市物流中心对接,连接成网。物流中心与下一级的配送节点相连,使用地下物流传输货物。
第二级为配送节点。配送节点与各个小区、商业聚集区、产业园直接或间接相连,使用地下物流系统传输货物,并可通过社区配送管道直达用户门口,如图2所示。
地下物流传输还可以从以下方面进行优化。每个物流单元可配置物联网芯片[2],实现实时定位、采集该单元的位置信息。地下物流管道应采用双通道设计,双向传输,可进行物流配送,亦可实现物流收件。地下物流管道加设可寻址的信号传输装置,方便发现故障、定位故障、解决故障。地下物流系统加入流量控制算法和拥塞处理算法,便于动态规划,提升物流传输效率。
2 网络节点选择
目前已有很多专家和学者对地下物流节点的选取进行了研究,王苏林等使用贪心遗传算法对地下物流节点的选择规划进行了研究[3],何永贵使用基于成本优化的算法对城市地下物流节点选址进行了研究[4],方龙祥分别使用基于贪心算法[5]和0~1整数规划算法对城市地下物流系统网络节点选址进行了研究[6],李姗珊使用基于地下管道物流运输的轨道线网规划与线路设计研究[7]。本文采用求解最短路径的经典算法——Dijkstra算法对配送过程中路径节点的选择进行了分析研究,实现了最短配送路径的求解。
2.1 网络节点选取背景
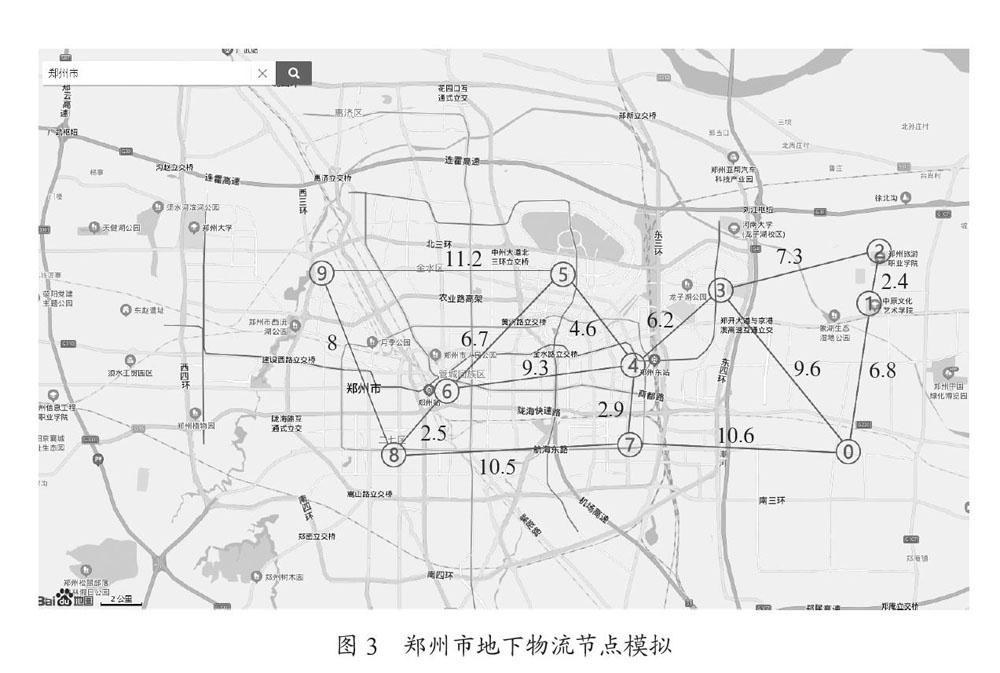
城市地下物流系统主要由一级物流中心、二级配送节点和各节点间的地下运输管道构成。一级节点之间互通互达,形成网络,并可相互之间传输货物。二级节点只与本区域的上级节点相连。二级节点与货物需求点直接相连或经转运点间接相连。由于需求末端错综复杂,地下物流管道的布置不可能都与二级节点直接相连,如图3中的节点,二级节点0,要为需求点4配送货物,可能的配送路线经过了节点1、节点2、节点3,然后到达需求点4,我们称节点1、节点2、节点3为转运点,也叫路径节点。
城市的需求点非常多,分布多集中在小区,商业聚集区等。本文研究的网络节点选取是在已知需求点和配送节点具体位置的情况下,如何选取合适的节点,实现最高的货物运转效率。由于使用地下物流传输系统进行传输,我们可以不必考虑堵车等其他因素造成的系统拥堵情况,那么最核心的问题就是如何在众多的网络节点中,查找出一个配送节点到需求点的最短路径。
2.2 数据来源
我们对郑州市的地下物流节点进行了设计,并从地图上选取0至9共10个节点,其中节点0为二级配送节点,节点1至9为需求节点,并且对各个节点间的距离通过地图测量工具进行了测量,单位为km,如图3所示。
2.3 Dijkstra最短路径建模
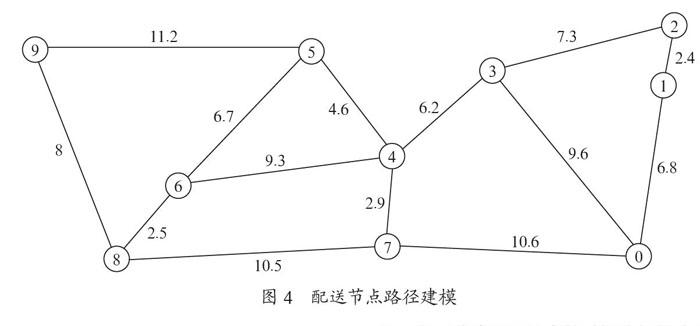
李健对Dijkstra最短路径算法进行了研究并优化了该算法[8],邹佰翰等人研究了最短路径算法在计算机网络路由选择中使用[9]。我们也使用Dijkstra算法对图3所示节点进行了建模分析。由图3可得到如图4所示的路径图。每条线都可以双向传输,实现货物的发件收件。现对货物的派发进行模拟求解,分别求出配送节点0至其他各需求节点的最短路径(至最终节点9结束)。如果是收件,用同样的方法亦可求解。
2.4 求解
求从节点0出发至终点节点9的最短路径。如表1所示,每一列为当前步骤最短路径求解结果,每经一个步骤,都能求出当前一步所对应的最短路径及所经节点,最后一行vj就是该步骤所选中的最短路径的结果。表格中的短横线“----”表示,已经求解出至该节点的最短路径,并添加至已知结点内,不用再计算该节点。
求解过程:设有已知集合S、未知集合T,初始情况S仅有v0节点,其余节点都在未知集合T里。从v0节点开始,一步一步求解能达到的最近的节点。最终可求出v0到其他各节点的最短路径。
步骤1:已知集合S:v0。
未知集合T:v1,v2,v3,v4,v5,v6,v7,v8,v9。
求出从v0节点出发到能直接可达的各节点的距离,将其填在最终结果表中的步骤1列中,如果不能直接可达,则记录为∞。
可得出最短路径为
步驟2:已知集合S:v0,v1。
未知集合T:v2,v3,v4,v5,v6,v7,v8,v9。
以v1节点为中间节点,求出从v0节点出发经v1节点到能直接可达的未知节点集合T中各节点的距离,填在最终结果表中的步骤2列中,如果不能直接可达,则记录为∞。由于v1节点已在已知节点中,不用重新计算,直接加上“----”符号,作为不再计算的标记。如果从v0出发,经过中间节点v1,去未知节点中寻找,如果也不可达,把前一列的结果移入当前单元格内。
按上述规则,求解可达的每一个未知节点的距离。
可得出最短路径为
步骤3:已知集合S:v0,v1,v2。
未知集合T:v3,v4,v5,v6,v7,v8,v9。
求出经v2节点直接可达的未知集合中各节点的距离,填在最终结果表中的步骤3列中,如果不能直接可达,则记录为∞。如果不可达,可从前一列中移植过来。
可得出最短路径为
步骤4:已知集合S:v0,v1,v2,v3。
未知集合T:v4,v5,v6,v7,v8,v9。
求出经v3节点直接可达的未知集合中各节点的距离,填在最终结果表中的步骤4列中,如果不能直接可达,则记录为∞。如果不可达,可从前一列中移植过来。
可得出最短路径为
步骤5:已知集合S:v0,v1,v2,v3,v7。
未知集合T:v4,v5,v6,v8,v9。
求出经v7节点直接可达的未知集合中各节点的距离,填在最终结果表中的步骤5列中。
可得出最短路径为
步骤6:已知集合S:v0,v1,v2,v3,v7,v4。
未知集合T:v5,v6,v8,v9。
求出经v4节点直接可达的未知集合中各节点的距离,填在最终结果表中的步骤6列中。
可得出最短路径为
步骤7:已知集合S:v0,v1,v2,v3,v7,v4,v5。
未知集合T:v6,v8,v9。
求出经v5节点直接可达的未知集合中各节点的距离,填在最终结果表中的步骤7列中。
可得出最短路径为
步骤8:已知集合S:v0,v1,v2,v3,v7,v4,v5,v8。
未知集合T:v6,v9。
求出经v8节点直接可达的未知集合中各节点的距离,填在最终结果表中的步骤8列中。
可得出最短路径为
步骤9:已知集合S:v0,v1,v2,v3,v7,v4,v5,v8,v6。
未知集合T:v9。
求出经v6节点直接可达的未知集合中各节点的距离,填在最终结果表中的步骤9列中。
可得出最短路径为
从最终结果表的最后一行vj行中,可得到从v0出发点,到可达的各个需求点的最短路径。
2.5 选择结论
经过最短路径求解——Dijkstra算法的求解,得到配送节点v0至各节点的最短路径以及所经过的节点分别为:
从v0出发至v1节点:
从v0出发至v2节点:
从v0出发至v3节点:
从v0出发至v4节点:
从v0出发至v5节点:
从v0出发至v6节点:
从v0出发至v7节点:
从v0出发至v8节点:
从v0出发至v9节点:
求出配送点至需求点的最短路径后,可生成一张最短路径表,并将该路径表存入系统内,当配送路线出现故障或阻塞后,可重新生成最短路径,更新最短路径表。下次配送时可直接查表选择最短路径节点进行配送,提升配送效率。
3 结 论
本文通过针对城市中二级配送节点进行配送时的节点选择进行建模,并使用最短路径算法——Dijkstra算法,对模型数据进行了分析。通过分析,可以得到从配送节点出发,到可达的每一个需求点的最短路径,以及该路径所经过的中间节点。此外,提出路径缓存的概念,将已计算的最短路径存储为最短路径表,提升路径选择的效率。该方法适用于针对任何二级节点进行配送时的节点选择问题。
参考文献:
[1] 吴晓钊,王继祥.物联网技术在物流业的应用现状与发展前景 [J].物流技术与应用,2011,16(2):53-56+59.
[2] 王继祥.物联网发展推动中国智慧物流变革 [J].物流技术与应用,2010,15(6):30-35.
[3] 王苏林,邱菲尔,陈凡,等.基于贪心遗传的地下物流节点选择规划研究 [J].工业工程,2020,23(5):88-95.
[4] 何永贵,周颖.基于成本优化的城市地下物流节点选址研究 [J].管理现代化,2018,38(6):66-69.
[5] 方龙祥,于雪雨.基于贪心算法的城市地下物流系统网络节点选址 [J].巢湖学院学报,2019,21(6):51-58.
[6] 方龙祥,于雪雨.基于0-1整数规划算法的城市地下物流系统网络节点选址 [J].安徽工程大学学报,2019,34(5):53-58.
[7] 李姗珊,刘延君,秦宇豪,等.基于地下管道物流运输的轨道线网规划与线路设计研究 [J].中国管理信息化,2019,22(14):92-93.
[8] 李健.基于Dijkstra最短路径算法的优化研究 [J].渭南师范学院学报,2009,24(5):61-64.
[9] 邹佰翰,张吉懿,苑晓兵.最短路径算法在计算机网络路由选择中的应用研究 [J].电声技术,2020,44(2):59-60+70.
作者簡介:周冰(1981—),男,汉族,河南温县人,副教授,硕士,研究方向:智慧城市、计算机应用。

