排出器动力学特性对斯特林制冷机性能影响分析

曲家闯，闫春杰，许国太，庄昌佩，张 安，张学林

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

斯特林制冷机是空间红外遥感系统的关键设备，主要为红外探测器提供低温环境，可以有效降低探测器的信噪比，提高灵敏度。斯特林制冷机分为调相结构和无调相结构纯气动的斯特林制冷机。纯气动调相制冷机结构紧凑、可靠性高；纯气动调相的斯特林制冷机的主要问题是如何维持排出器的运动及与压缩机活塞运动有合适的相位关系。排出器的相位只能通过调节排出器的质量和板弹簧的刚度被动调节[1]，排出器的运动和与压缩机的活塞运动相位角这两个参数直接影响着斯特林制冷机的性能。本文期望通过建立斯特林制冷机的热力学、动力学模型来研究排出器的质量及板弹簧刚度对整机性能的影响，找出其最佳值，提高斯特林制冷机的性能。

1 斯特林制冷机的模型建立

1.1 分置式斯特林制冷机结构

机械驱动的斯特林制冷机按照结构布置不同可分为整体式和分置式两种[2]。分置式斯特林制冷机（牛津型）的压缩机与排出器分开放置，如图1所示，两者之间通过细管连接，可以有效地减少压缩机的振动对制冷机冷头的影响，明显降低排出器的振动指标；压缩机与膨胀机均采用间隙密封、柔性板弹簧支撑。

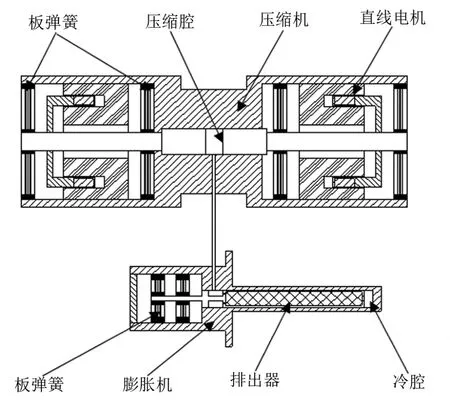
图1 分置式斯特林制冷机结构示意图Fig.1 Schematic diagram of split Stirling refrigerator

1.2 等温模型建立

采用等温分析模型建立斯特林制冷机的热力学模型，假设：

（1）压缩腔和膨胀腔中进行的是等温过程，即等温压缩过程和等温膨胀过程；

（2）压缩腔和膨胀腔的容积按正弦规律变化；

（3）工质遵守理想气体状态方程，即pV=MRT；

（4）回热过程是理想的，不考虑不可逆损失；

（5）整个系统中的瞬时压力相同；

（6）各工作腔内的温度均匀一致。

根据假设，得出制冷机的理论制冷量Qc为：

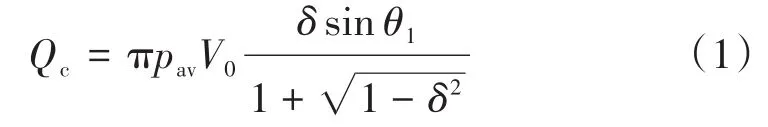
式中：δ无物理意义；pav为制冷机运行过程中的平均压力，Pa；V0为排出器扫气容积，m3；θ1为压力波之间相位角，rad；

令：

式中：τ为热端与冷端温度比；λ为容积比即压缩机活塞扫气容积与排出器扫气容积之比；φ为排出器领先压缩机活塞的角度（活塞相位角）；s为相对死容积。

式中：∑Vd,i为总空容积，m3；Vd,i为各死容积，m3；Ta为压缩腔温度，K；Tc为冷腔温度，K；Td,i为各死容积内的气体温度，K。

试验表明，斯特林制冷机的实际制冷量Qr只有等温模型计算值的30%[1]，即：

活塞相位角φ和排出器与压力波之间相位角θ之间的关系如式（5）：

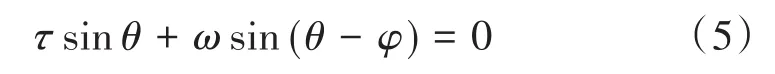
式中：ω为排出器往复运动的角频率rad/s。

1.3 排出器动力学模型建立

排出器是斯特林制冷机的关键部件，通过排出器（回热器）传递的热量比制冷机的制冷量大很多（约10～50倍），所以，排出器参数特性对制冷机的制冷性能起决定性的影响。将排出器受压力波推动做往复运动的过程设为是单自由度系统在简谐激励下的振动，则可知压力波与排出器的相位角、排出器的振幅、系统的临界阻尼、系统固有频率分别为[2]：

式中：c为排出器运动过程中受到的阻尼，N（/m/s）；k为排出器连接的板弹簧刚度，N/m；mp为排出器质量，kg；xp为排出器往复运动的振幅，m；F0为压缩机产生的压力波使排出器所受到的力的振幅，假定压力波为正弦波，则F0=A（rpmax-pav），N，其中Ar为排出器阶梯杆面积，m2；cc为临界阻尼，N（/m·s-1）；fn为排出器固有频率。

2 仿真计算及结果分析

在1.2、1.3中分别建立了斯特林制冷机的热力学模型及排出器动力学模型，两个模型通过压缩机活塞相位角φ和排出器与压力波之间相位角θ建立起了联系，并通过式（5）耦合。计算时先假定排出器初始振幅和系统阻尼不变，通过排出器动力学方程求出排出器与压力波的相位角θ，进而求出活塞相位角，并根据等温模型求出压力波幅值，再将压力波结果带回动力学方程，并求出排出器振幅，反复迭代，并将假定的排出器振幅值与动力学计算值进行对比，当二者差值在一定范围内时结束迭代，输出结果。

2.1 排出器板弹簧刚度对系统的影响

排出器板弹簧刚度影响排出器振幅及相位进而影响整机的制冷量。保持整机的运行频率、排出器质量不变，逐渐增大排出器板弹簧刚度，制冷量及相位角的变化如图2所示。从变化曲线可以看出，随着板弹簧刚度的增大，相位角逐渐减小，且减小趋势越来越弱；而制冷量则是由小变大再变小，出现一个峰值，此时制冷量最大，整机输出状态最优，对应的板弹簧刚度为5 500 N/m，相位角约为72°。即在制冷机设计、调试过程中，每一组参数对应一个最佳排出器板弹簧刚度，此时制冷机在这一组参数下制冷量最大。

图2 制冷量及相位角随板弹簧刚度变化曲线Fig.2 Variation of refrigerating capacity and phase angle with flexure spring stiffness

排出器振幅随板弹簧刚度变化曲线与制冷量的变化规律一致，同在5 500 N/m处有最大值，此时排出器的固有频率与运行频率比约为0.85，如图3所示。

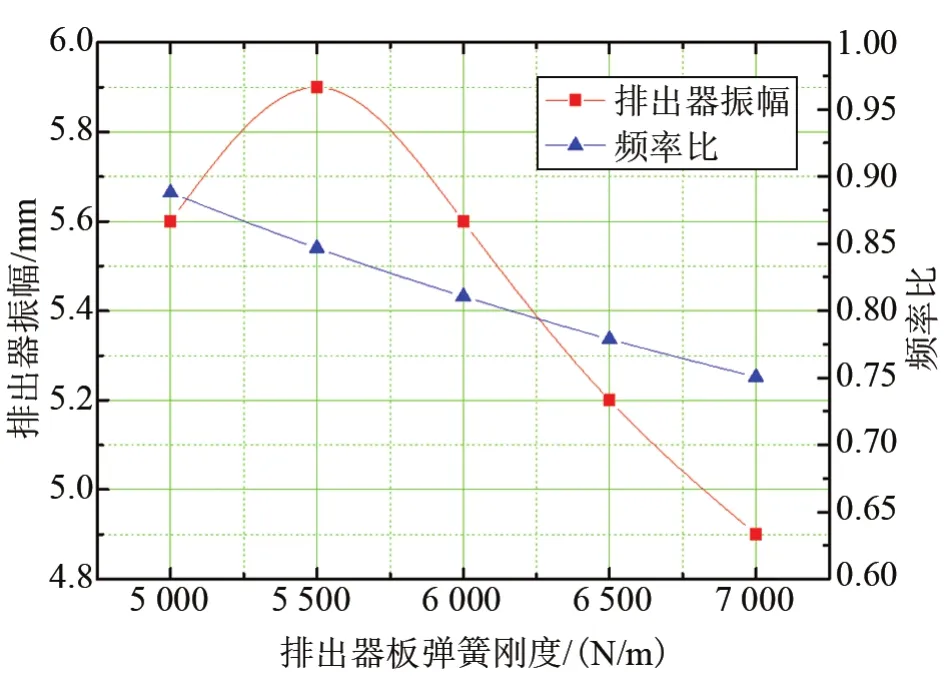
图3 排出器振幅随板弹簧刚度变化曲线Fig.3 Variation of displacer amplitude with Flexure spring stiffness

2.2 排出器质量对系统的影响

制冷机的制冷量以及相位角随排出器（回热器）质量的变化曲线如图4所示。随着排出器质量变大，制冷量先增大再减小，存在一个最佳质量使得制冷量最大，而随着排出器质量变大，其固有频率减小，逐渐接近运行频率，故相位角逐渐变大；令ε为排出器的固有频率与运行频率的比值，ε=fn/f，其中fn为排出器固有频率，f为制冷机运行频率，则排出器的振幅随频率比的变化曲线如图5所示。当频率比约为0.85时，振幅有最大值。

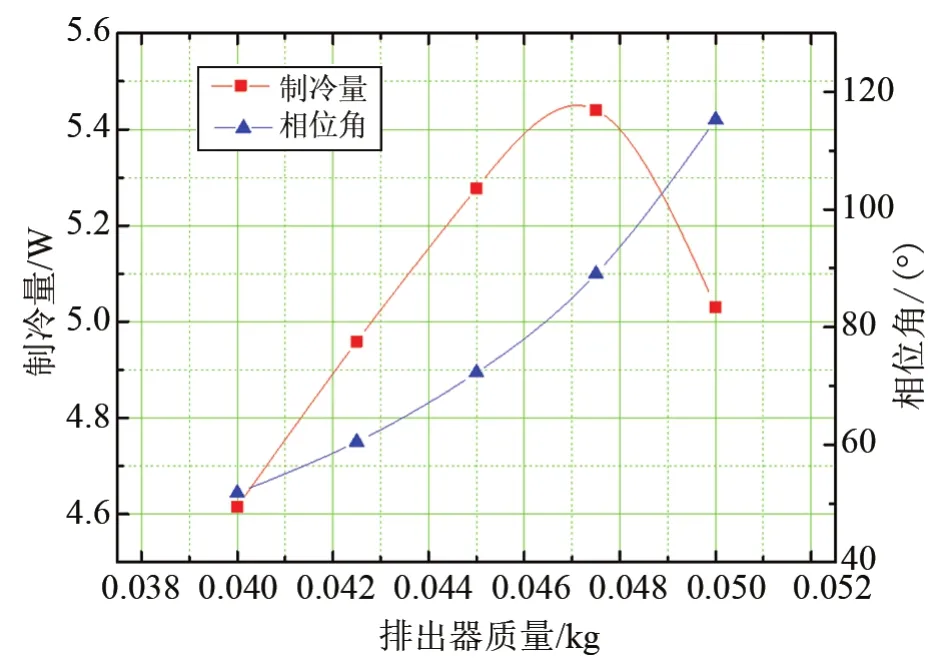
图4 制冷量及相位角随排出器质量变化曲线Fig.4 Variation of refrigerating capacity and phase angle with displacer mass

图5 排出器振幅随频率比变化曲线Fig.5 Variation of displacer amplitude with frequency ratios

2.3 临界阻尼对系统的影响

同时变化板弹簧刚度与排出器质量，保持排出器的固有频率不变，维持排出器频率比为0.85，系统的制冷量随临界阻尼变化如图6所示。可以看出，虽然频率比不变，但随着临界阻尼变大，系统的制冷量递减，说明在相同的频率比下，排出器的质量越小，制冷量越大。

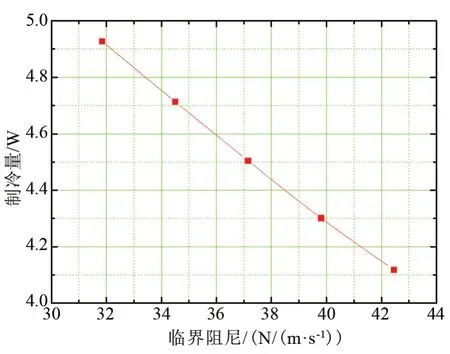
图6 制冷量随临界阻尼变化曲线Fig.6 Variation of refrigerating capacity with critical damping

3 结论

建立了分置式斯特林制冷机热力学及动力学模型，通过两个模型的耦合计算，对排出器的动力学特性与系统的制冷量、排出器振幅、相位角等的影响进行了分析讨论，得出以下结论：

（1）排出器的板弹簧刚度存在一个最佳值，使得系统的制冷量最大。在本模型中，当制冷量最大时，排出器振幅有最大值，随着板弹簧的刚度增大，活塞相位角逐渐减小；

（2）随着排出器质量增大，系统的制冷量先增大再减小，当频率比为0.85时，排出器振幅最大，说明在制冷机设计及调试时，须选定合适的排出器频率比，使整机的制冷量最大；

（3）保持频率比在最佳值时，排出器的临界阻尼变大，系统的制冷量仍然会减小，表明，在设计斯特林制冷机时尽可能减小排出器的质量有益于提高制冷量；当排出器质量确定后，须确定最佳的频率比，以此计算出排出器板弹簧刚度，使膨胀机的性能最优。