采用视觉伺服的月球样品容器夹持控制方法

金晟毅，姚 猛，邓湘金，郑燕红，赵志晖，王晓丹

(1.北京空间飞行器总体设计部，北京 100094；2. 航天东方红卫星有限公司，北京 100094)

0 引 言

嫦娥五号探测器着陆月面并完成月球浅表层月壤样品采集，之后需利用采样机械臂及其末端执行机构夹持盛装有月壤样品的样品容器，转移入安装在探测器上升器部分的密封容器中，随上升器从月面起飞，最终返回地球。

利用机械臂及其末端执行机构夹持盛装月球表层样品的样品容器，是嫦娥五号探测器月面采样封装任务的关键环节之一[1]，该环节的执行和操控对机械臂末端执行机构与样品容器的相对位姿精度及运动轨迹的稳定性有极高的要求，其运动学与动力学之间存在较强的耦合关系。受月面低重力及探测器本体姿态等不可预知因素的影响，其动力学模型的精确性无法有效评估，单纯依靠逆运动学模型通过关节旋变传感器测量值和机械臂D-H参数确定的机械臂末端执行机构位姿结果可信度较低，不能满足安全夹持样品容器的控制决策需求。因此，需借助视觉伺服控制的方法对机械臂末端执行机构与被夹持样品容器之间的相对位姿进行精确测量，并以此为基础实现轨迹跟踪和定位控制。

传统的基于图像的视觉伺服(Image based visual servoing, IBVS)[2]和基于位置的视觉伺服(Position based visual servoing, PBVS)[3]有着一定的局限和不足[4]。PBVS对标定和模型的精度有较高的依赖，当控制目标脱离相机视场后将会失效，IBVS可直接使用图像特征进行伺服控制，但由于相机安装于机械臂上与机械臂系统有强耦合性，图像雅可比矩阵的奇异点难以规避，存在局部最小值[5]。为克服上述两种视觉伺服方法的缺陷，确保夹持样品容器的精度和安全性，本文提出了视觉伺服样品容器夹持的控制方法和系统，解决任务中相对位姿精度及运动轨迹的稳定性要求。

本文介绍了固定安装相机和“眼在手”相机协同获取机械臂末端执行机构以及样品容器特征的混合视觉伺服系统，同时为了避免月面光照、漫反射及目标特征被遮挡等因素影响，采用了基于扩展卡尔曼滤波的方法对机械臂末端执行机构与样品容器之间相对位姿的非线性估计。通过在轨实际应用情况分析，证明了该系统和方法设计的合理性和有效性。

1 视觉伺服系统模型

机械臂末端执行机构夹持样品容器0°和90°视角观察的示意图如图1所示，采集到的月壤样品装入样品容器后样品容器封盖，安装在机械臂末端的末端执行机构需要夹持容器盖上部的帽檐结构，从而将样品容器提起并转移至安装在上升器上的密封容器之中[6]。此处容器盖上的帽檐结构与容器盖距离约为5 mm，为了样品容器夹持的安全，夹持需以容器盖上的帽檐结构的中心部分为基准，抓取机构抓取位置的垂直方向偏差应≤2.3mm，水平方向偏差应≤1mm，抓取机构姿态与样品容器同轴偏差需≤3′。

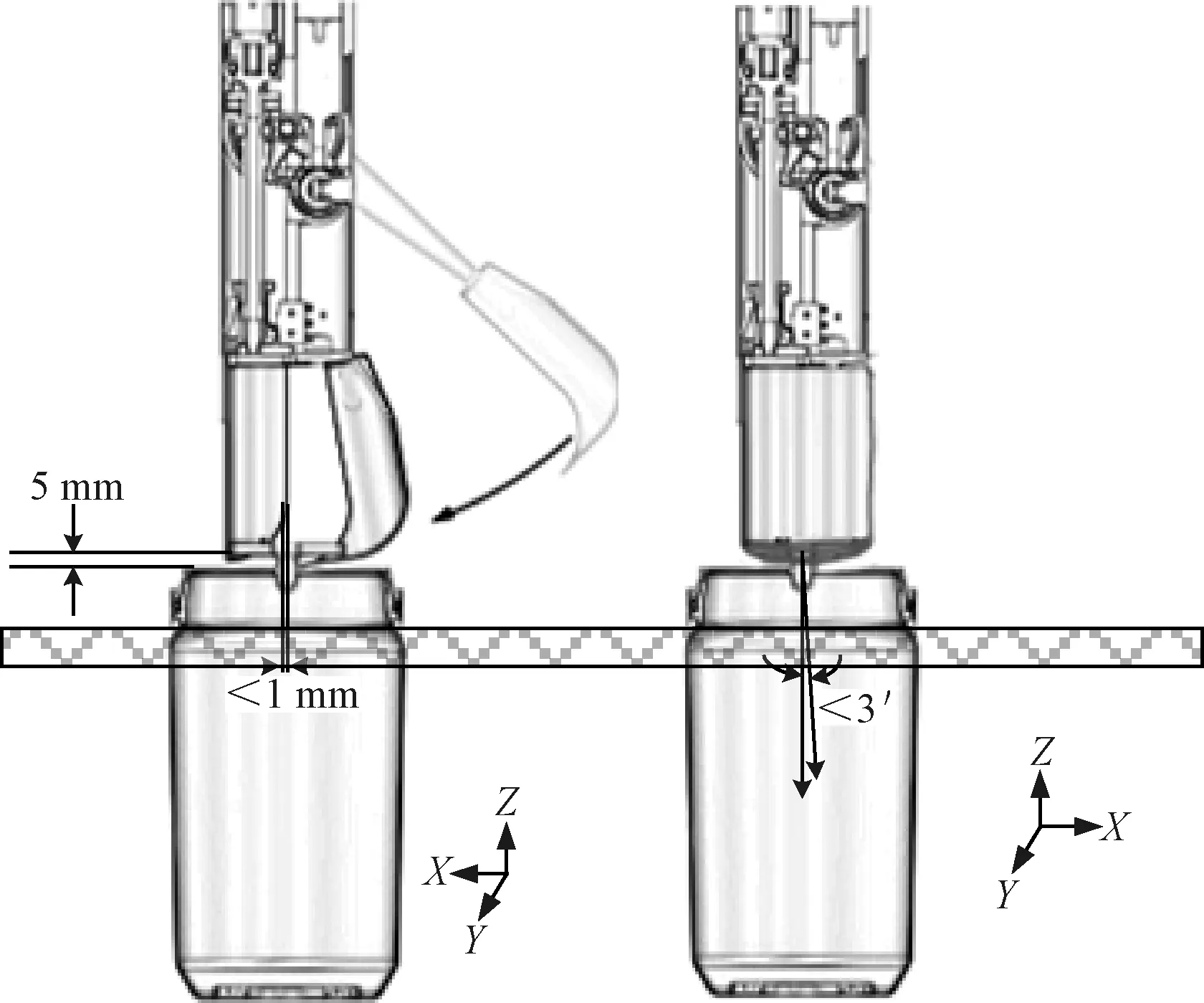
图1 夹持样品容器示意图Fig.1 Schematic diagram of gripping sample container

受到月面重力等外界环境因素的影响，机械臂的动力学和运动学建模偏差，不能满足安全夹持样品容器的控制决策需求。

1.1 机械臂夹持容器建模

夹持样品容器的机械臂采用四自由度设计，设置有肩偏航关节、肩俯仰关节、肘俯仰关节、腕俯仰关节、臂杆A、臂杆B和末端执行机构，每个关节上配有关节角度测量传感器用于测量各个关节的转动角度[7]。

如图2所示，“·”表示关节安装位置;“∘”表示固定安装或连接位置;θ1为肩偏航关节转动角度、θ2为肩俯仰关节转动角度、θ3为肘俯仰关节转动角度、θ4为腕俯仰关节转动角度;a2为臂杆A的长度，a4为臂杆B的长度;a0、a1、a3、a5分别为关节质心与连接的相对位置。设置机械臂基坐标系M(X,Y,Z)，机械臂安装位置与M坐标系原点重合；J1(x1,y1,z1),…,J4(x4,y4,z4)分别为各自关节的坐标系，其原点为关节质心。HE(xEE,yEE,zEE)为机械臂末端执行机构坐标系与腕俯仰关节坐标系J4(x4,y4,z4)重合，当各机械臂关节角度取Θ(t)=[θ1,θ2,θ3,θ4]T时定义机械臂末端执行机构在M坐标系下的位姿为[xe,ye,ze,θe]T=ETM(Θ(t))。定义Θ(t)=f(*)为机械臂逆运动学变换函数。

图2 机械臂关节坐标示意图[7]Fig.2 Joint coordinate diagram of manipulator[7]

1.2 样品容器加持映射建模

执行样品容器夹持时所需的坐标系和系统映射关系示意图如图3所示，系统设置有固定安装相机FC以及安装在机械臂末端执行机构上的“眼在手”相机MC。

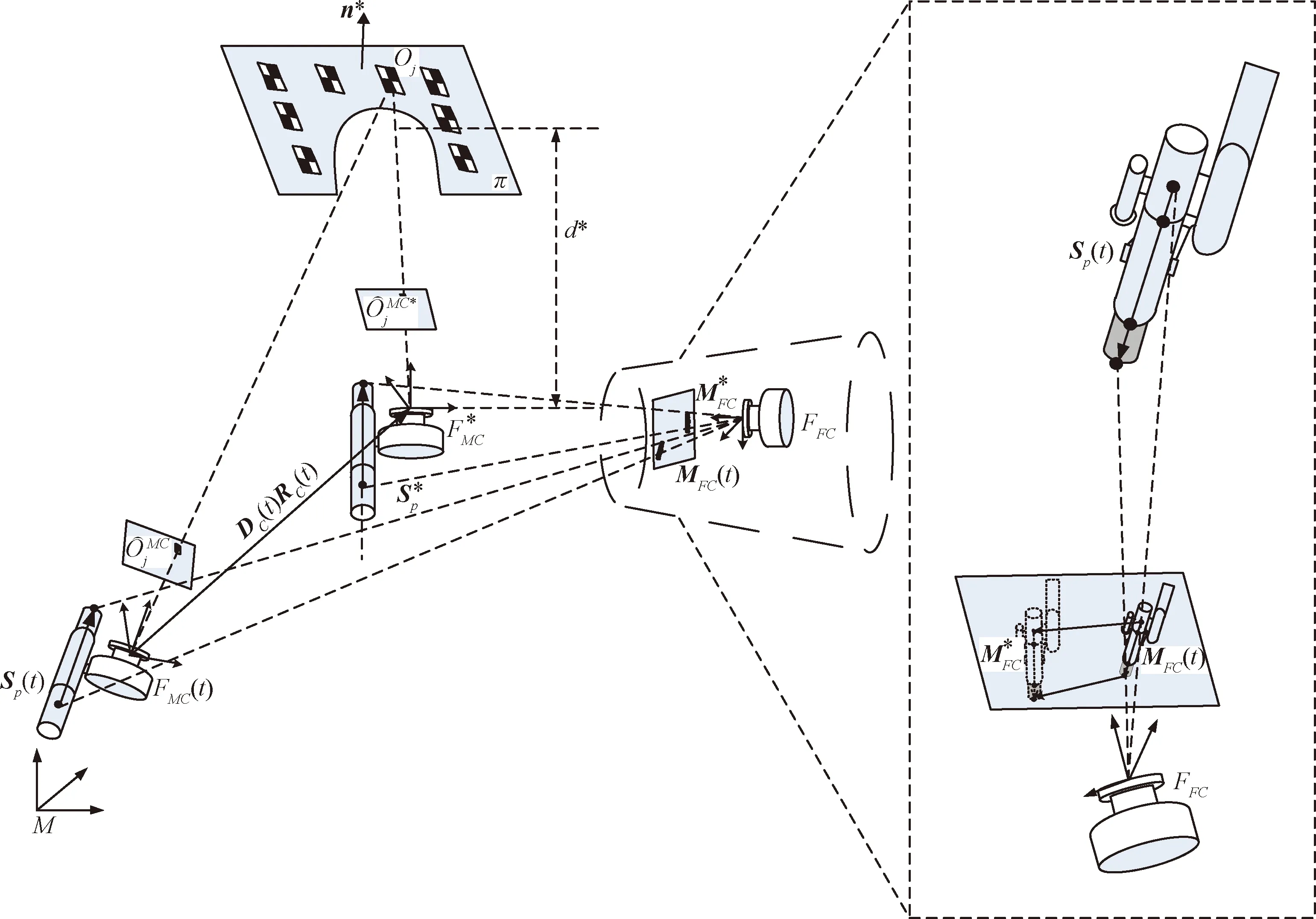
图3 坐标系和系统映射关系示意图Fig.3 Schematic diagram of coordinate and mapping system relationship

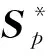
(1)

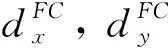
(2)

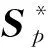
(3)

样品容器及特征面关系示意图如图4所示。

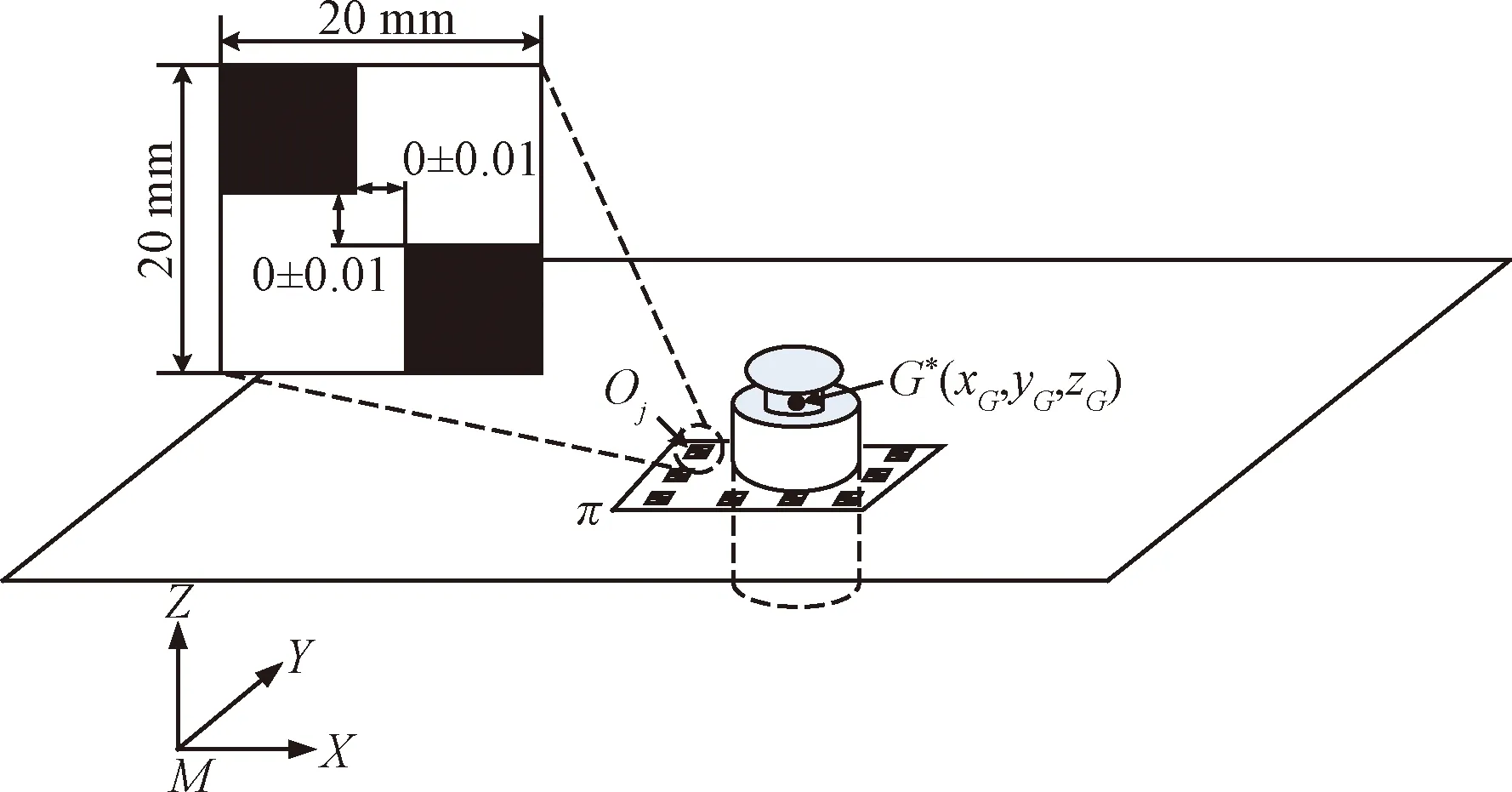
图4 样品容器及特征面关系示意图Fig.4 Schematic diagram of relationship between sample container and characteristic surface

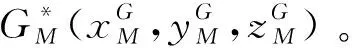
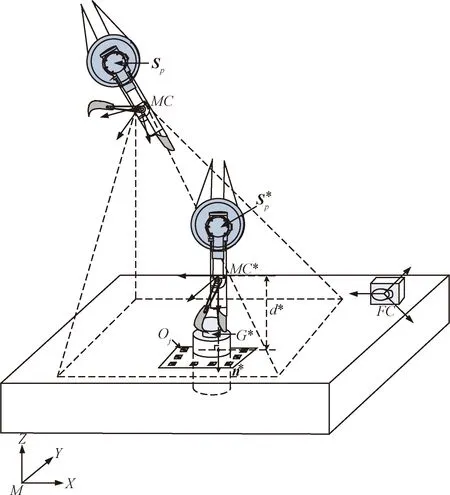
图5 夹持样品容器过程Fig.5 Gripping sample container process

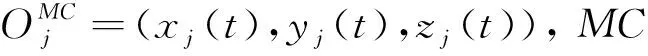
(4)

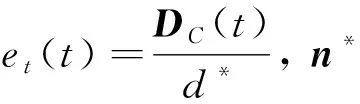
2 基于EKF的控制量估计

月面光照、探测器防热多层漫反射及目标特征被遮挡等因素会影响相机对目标的检测和识别，使计算机械臂控制参数时产生抖动和丢失[8]。卡尔曼滤波算法可根据当前系统状态，结合实际测量值联合估计下一时刻系统状态，更新迭代可以很好的解决这一问题[9]。

扩展卡尔曼滤波(Extended Kalman filter, EKF)将非线性系统线性化，然后采用卡尔曼滤波框架进行状态信号滤波和估计[10]。适合于本文所提的非线性视觉伺服系统，EKF的状态和观测方程为：

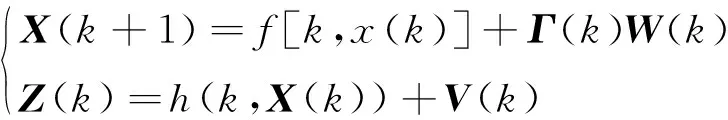
(5)

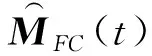
(6)

对于机械臂末端执行机构和控制目标之间的相对位姿的估计，包含了相对位移和速度。

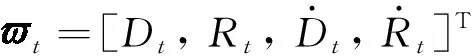
(7)

其中:A是系统状态转移矩阵，Zt是系统观测向量，F(*)为观测模型函数，qt和rt分别是系统和测量噪声，A定义为：

(8)

I4是一个4×4的单位矩阵，04是一个4×4的零矩阵，Δt是系统采样时间。

对应的系统观测模型函数为：

(9)

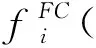
扩展卡尔曼滤波过程中预测阶段有：

(10)

Σt|t-1=AΣt-1AT+Qt-1

(11)

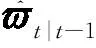
(12)

扩展卡尔曼滤波过程中更新阶段有：

(13)

(14)

(15)

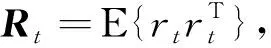
3 实施场景与结果

2020年12月02日，嫦娥五号探测器在月面完成表面样品采集后，19∶31转入样品容器夹持工作过程。在相机FC和MC的视觉伺服系统支持下，机械臂末端执行机构在M坐标系下的轨迹曲线，运动轨迹平滑稳定如图6所示。

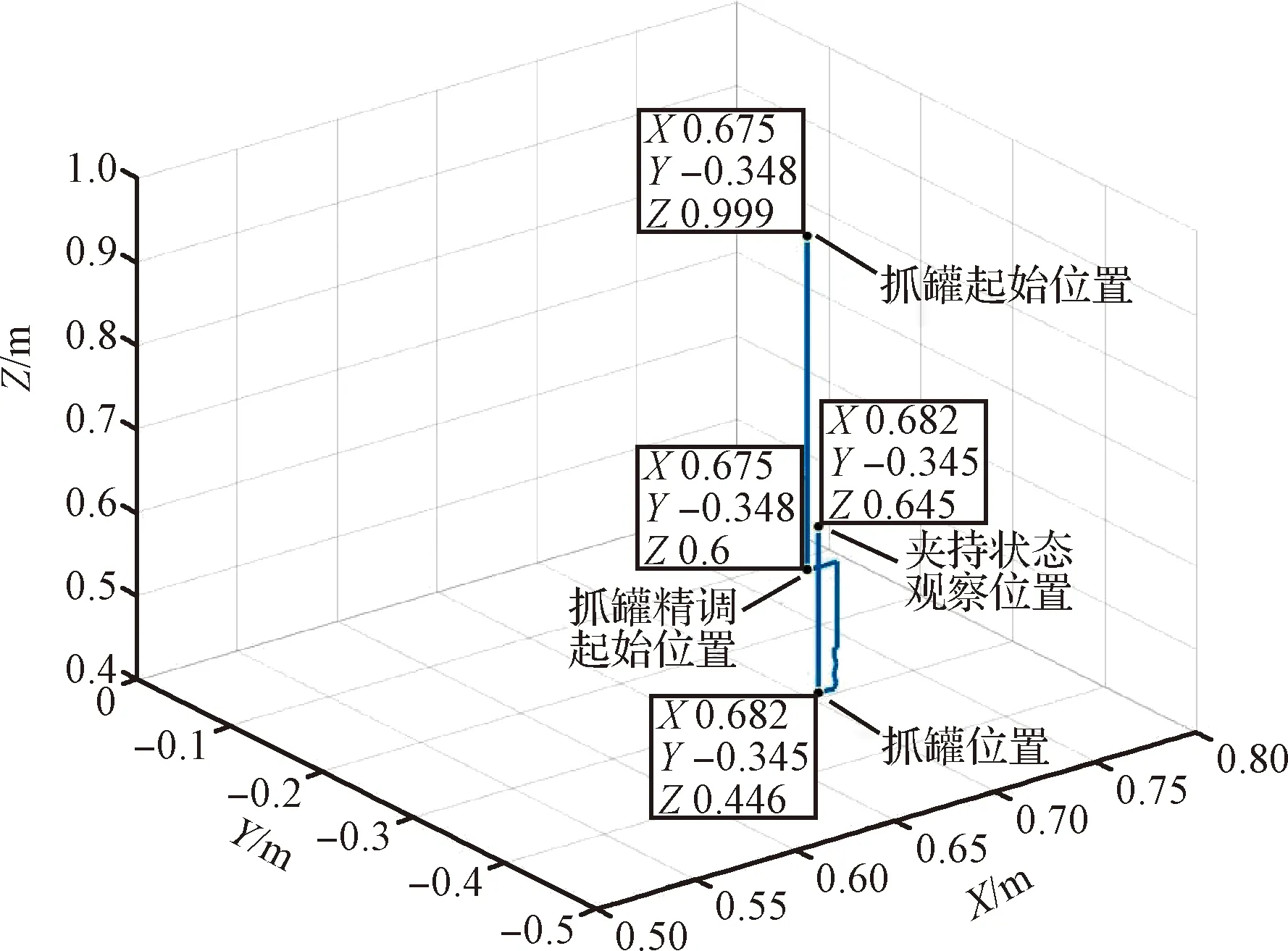
图6 夹持样品容器过程机械臂末端执行机构运动轨迹Fig.6 The movement trajectory of the manipulator end actuator in the process of gripping the sample container

从样品容器夹持初始位姿(0.675 m，-0.348 m，0.999 m，89.89°)开始，t时刻位姿记录为(0.675 m，-0.348 m，0.6 m，89.94°)，最终到达容器夹持目标位姿(0.682 m，-0.345 m，0.446 m，90.00°)，并在该处进行样品容器夹持。

图7 容器夹持过程目标映射关系Fig.7 The mapping of the gripping container process

图8 样品容器夹持状态判断Fig.8 The determination of state of the gripping sample container

4 结 论

本文提出的采用视觉伺服方法，解决了月面采样机械臂精确夹持样品容器的控制问题。利用固定安装相机和“眼在手”相机获取机械臂末端执行机构以及样品容器特征，协同完成机械臂末端执行机构位姿以及到达目标夹持位姿的控制量确定，采用扩展卡尔曼滤波补偿算法对控制量进行准确估计，使机械臂末端执行机构在样品容器夹持过程中运行轨迹平滑。最后，通过对在轨月面真实样品容器夹持效果分析，验证了该视觉控制方法的有效性。