基于决策树的多防御方目标攻防决策

阙养华，冮铁强，陈立杰

(厦门大学航空航天学院，厦门 361000)

0 引言

目标攻防博弈(Target Strike and Defense)不同于一般的追逃博弈，因为此时博弈的各方角色已经发生了变化。攻击方的任务是在确保自身安全的前提下打击到目标，而防御方的任务是保护目标不被攻击方打击，并且尝试在攻击方打击到目标前将其拦截。这些变化使得对目标攻防博弈的求解变得更困难。Isaacs在其著作《Differential games》中提到了一个简单的目标攻防问题。Boyell在导弹合作作战的背景下分析了这类情况。Ratnoo等和Shima提出防御方使用视线引导策略拦截攻击导弹。Zhang等研究了逃避者试图穿过两个追捕者之间的博弈问题，利用定性微分对策推导出界栅的存在，并得出逃避者和捕获者的最优策略。Liang等在此基础上将其中一个捕获者换成防御的目标，形成了三方(目标、攻击方、防御方)目标攻防问题，给出了界栅和各方的最优策略。Casbeer等、Garcia等和Shaferman等还研究了其他各种合作方式的目标攻防问题。目前来看，目标攻防研究集中在防御方时的防守问题，对于多防御方的目标攻防问题目前研究较少。当增加若干个防御方后，各防御方如何通过合作来达到任务的要求是当前需要解决的重点，这也是本文研究的多防御方目标攻防问题(Multi-Defender Target Strike and Defense)。

由于防御方数量增加，此时博弈的复杂度也提高了，因此引入决策树的思想将复杂的多防御方目标攻防问题转换成易于理解的决策树模型。决策树是一种基本的分类和回归方法，在分类问题中表示基于特征对实例进行分类的过程，分类模型是if-then规则的集合。决策树的分类模型比较符合人类的推理并且易于理解。决策树还具有分类速度快，模型具有可读性的优点。决策树算法的核心以ID3和C4.5算法为主，分别利用信息增益和信息增益率的大小来选择分类的候选属性，直到所有样本都完全分完为止。复杂的多防御方目标攻防问题一般很难直接确定各方需要采取的最佳策略，例如防御方是否需要采取合作策略，是否可以直接与目标会合。因此,各方决策的内部逻辑还需要进一步梳理清楚，以达到更快的态势判断和决策选择。

1 多防御方目标攻防问题

1.1 多防御方目标攻防问题模型

多防御方目标攻防问题的模型如图1所示。假设目标是静止的，攻击方和防御方的速度均为常速，分别为

V

和

V

，将攻击方和防御方的速度方向角度设为其控制变量，其运动学方程如下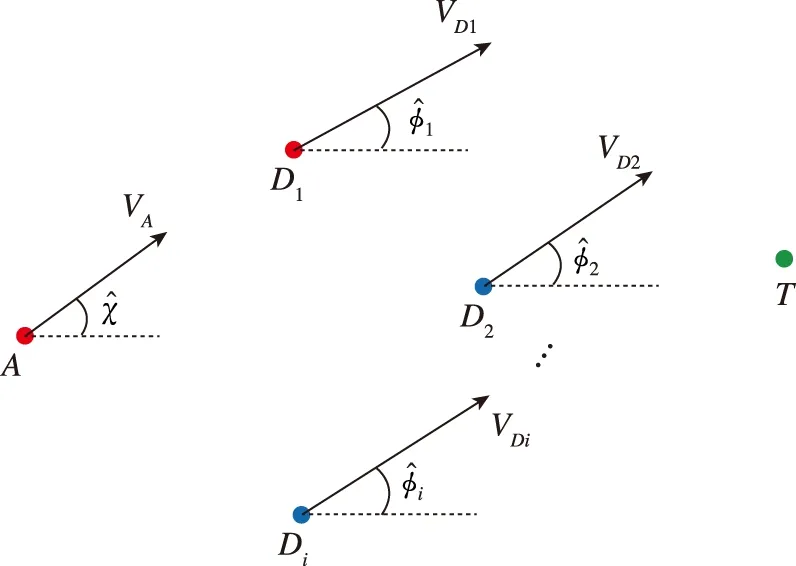

图1 多防御方攻防问题模型Fig.1 The model of multi-defender strike and defense

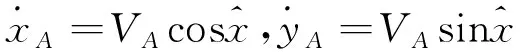
(1)

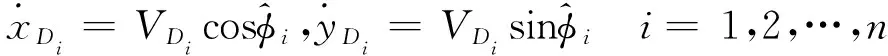
(2)

当

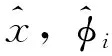
V

≥

V

时，防御方一定会将攻击方提前捕获。本文讨论

V

<

V

的情况，并用

α

=

V

/V

表示两者的速度关系。

为了简洁描述目标攻防博弈，以一个防御方为例，将三者间的相对关系作为状态量，如图2所示，新的方程可以写成

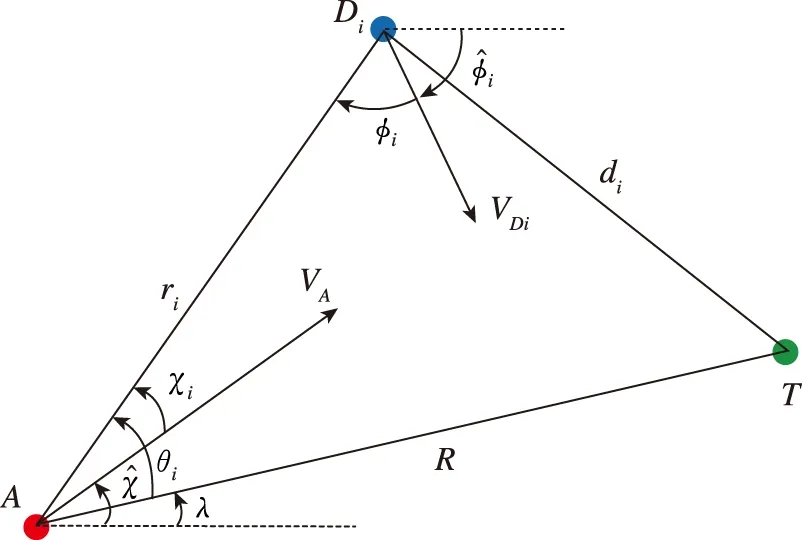
图2 三者相对位置关系Fig.2 The relative position of the three agents

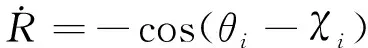
(3)

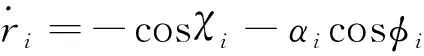
(4)

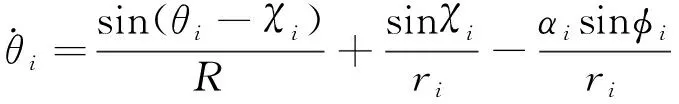
(5)

由Liang等研究成果得出，

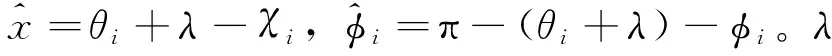
A

，

D

的最优控制策略为

(6)

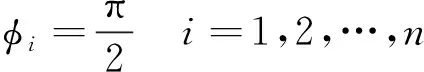
(7)

由Liang等研究成果得出，当攻击方初始状态位于攻击方获胜区域时，攻击方先采取式(6)、式(7)的策略躲避防御方的Apollonius圆，然后直接打击到目标，这一过程称为迂回策略。

考虑攻击方和防御方的捕获半径为零。防御方的目标是阻止攻击方打击到目标

T

，即

R

>0。与此相反，攻击方尽可能打击到目标

T

，并且还不能被防御方拦截到，即

R

=0,

r

>0。如果防御方能够在攻击方打击到目标

T

前就与目标

T

会合，也认为是防御方获胜，因为此时攻击方已经不可能在确保自身安全的前提下打击到目标

T

。

1.2 多防御方目标攻防的复杂性

对抗博弈问题中讨论和研究最多的是双方博弈，当博弈的数量增加到3个及以上时，问题的难度和性质都会发生变化。随着博弈参与方数量的增加，对抗博弈需要考虑的因素也增加，某一方无法像双方博弈时把注意力都只关注于对方，此时还需考虑其他参与方对自身的影响。由Liang等研究成果可知，当只考虑一个防御方进行拦截时，各方的最优策略只需要通过攻击方初始时的位置即可判断得出。当防御方增多时，问题就变得复杂。

当多个防御方参与目标攻防时，防御方除了能够拦截攻击方，还可以通过与其他的防御方进行配合，以完成单个防御方无法完成的任务，这也叫做“能力涌现”现象。

如图3所示，有的防御方选择合作，而有的防御方就会乘机在其他防御方一起去合作拦截攻击方的时候，选择直接与目标会合。这种群体所体现出来的智能行为无法再通过简单的单个参与方初始位置来判断。因此，本文提出引入决策树的思想对复杂的多防御方目标攻防问题的各方决策进行合理且快速的判断。为了应用决策树思想，需要对参与方的决策类别进行讨论。

图3 防御方群体智能行为Fig.3 Swarm Intelligence behavior of defenders

本文对两个防御方的目标攻防问题的决策进行讨论，说明在多防御方目标攻防问题中决策树的使用。首先通过训练样本集合训练决策树模型，再通过测试样本验证模型的准确性。

2 多防御方目标攻防问题的决策树分类模型

为了搭建决策树模型，首先需要对多防御方的目标攻防问题进行分类并确定分类的标签。这里将各方的策略作为分类的标准，以初始时刻的各方态势作为测试属性来搭建决策树模型。根据不同初始时刻态势，可以将各方的策略分为4类，分别用

S

,

S

,

S

,

S

表示。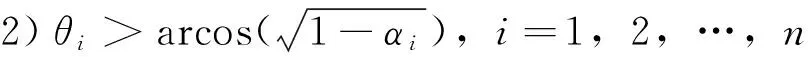

注意到防御方的地位是等价的，所以各方策略的分类表示为：

S

:

S

-

S

-

S

，

i

=1,2,3,4。

S

和

S

表示防御方的策略，

S

表示攻击方的策略。具体的策略(以字母

S

表示)中，Arbitrary表示任意策略，Straight表示采用直接朝向目标方向策略，RoundAbout表示采用式(6)、式(7)的策略，Parall表示攻击方采用平行四边形法则后的策略，Cooperation表示防御方采取合作策略，为了方便都使用首字母进行代替。

2.1 多防御方目标攻防问题的分类

2.1.1

S

:

A

-

A

-

S

图

2.1.2

S

:

S

-

A

-

A/A

-

S

-

A

如图5所示，当目标位于Apollonius圆内时，防御方可以直接朝向目标会合，此时攻击方无论采取何种策略都无法改变防御方获胜的结果。攻击方最好的办法也只能是尽可能靠近目标，以期对目标造成最大的威胁。从图5中可以看到，这类情况有3种，分别是目标位于某一个防御方的Apollonius圆内和位于两个防御方的Apollonius圆交集内。由于

D

D

等价，因此将这3类情况分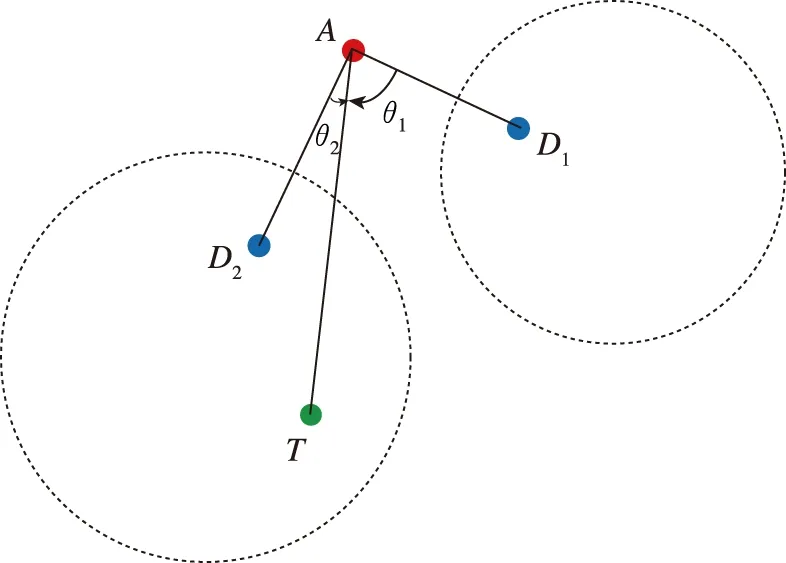

(a)

(b)

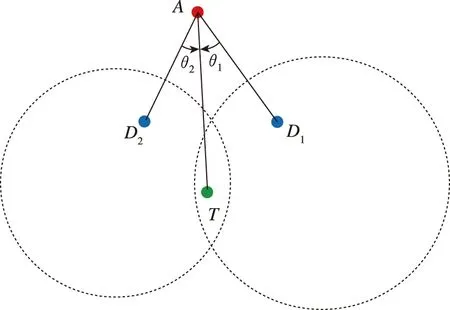
(c)图5 目标在Apollonius圆内Fig.5 The target is within the Apollonius circle

类为

S

:

S

-

A

-

A/A

-

S

-

A

，表示某一防御方采取直线朝向与目标会合的策略，攻击方无论采取何种策略都无法改变结果。2.1.3

S

:

C

-

R

-

P/R

-

C

-

P

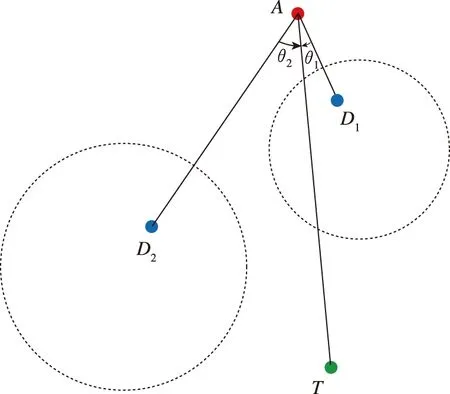
图

为了充分发挥防御方数量上的优势，提出一种合作策略，让防御方的目标变成使得其各自的Apollonius圆相切。如图7所示，黑色虚线圆代表初始状态的Apollonius圆，红色虚线圆代表相切时的状态。Apollonius圆相切后使攻击方无法直接通过两个防御方之间的空间，只能绕行更大的范围来达到摧毁目标的目的，从而增加了攻击方的燃料消耗。

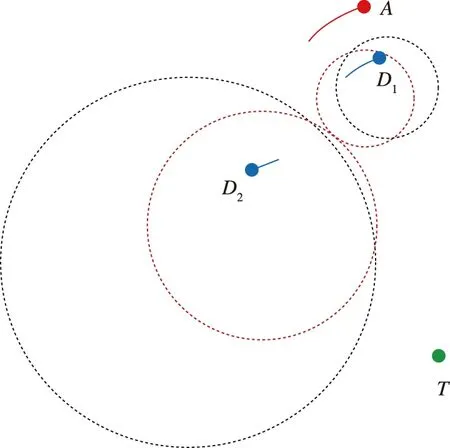
图7 两个Apollonius圆相切Fig.7 Two Apollonius circles are tangent

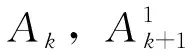
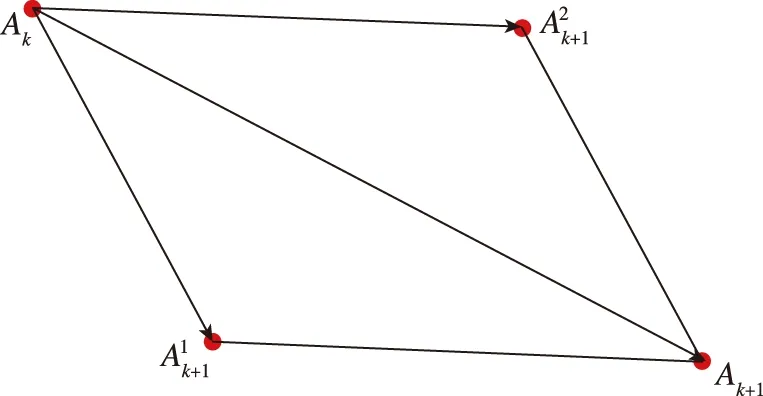
图8 平行四边形合成Fig.8 Parallelogram composition

(8)

W

,

W

是基于距离威胁的权重

(9)

同样，将

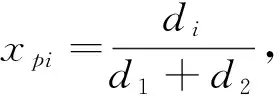
D

的运动离散化，在每个离散时间Δ

t

，其下一时刻的位置由

D

1,+1=

Round

-

About

(

A

,

D

1,)得出，

RoundAbout

策略由公式(6)和(7)确定。

D

的目标是尽快使

AD

的Apollonius圆与

AD

的Apollonius圆相切。可以得到初始时两圆最近点之间的距离表达式

(10)

其中,

用最速下降法求解下一步

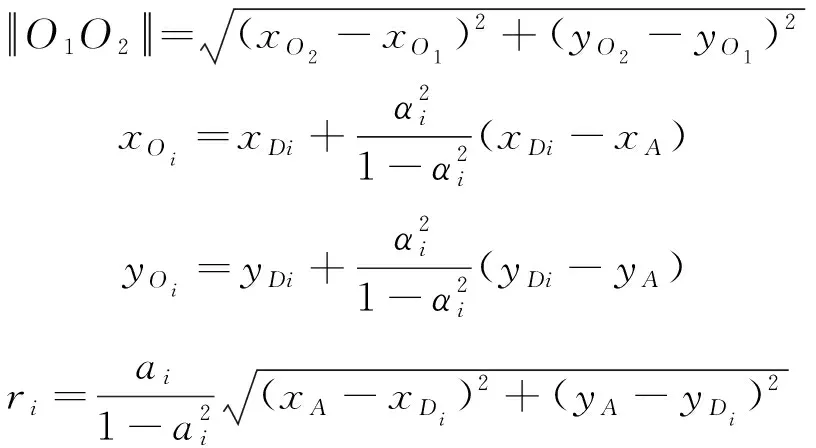
D

的运动方向，梯度向量和步长为

(11)

Δ

t

为离散步长，故

D

的迭代方程为

D

2,+1=

D

2,+

sd

()

(12)

2.1.4

S

:

S

-

R

-

R/R

-

S

-

R

除了使防御方的Apollonius圆相切外，另一种合作方式比较直观，某一防御方尽可能地拖住攻击方，另外一个防御方直接与目标会合。如图9所示，

D

单独去拦截攻击方

A

，而

D

直接朝向目标与其会合，这样的结果就是防御方获胜，因为攻击方采用迂回策略没有比

D

直接与目标会合更快。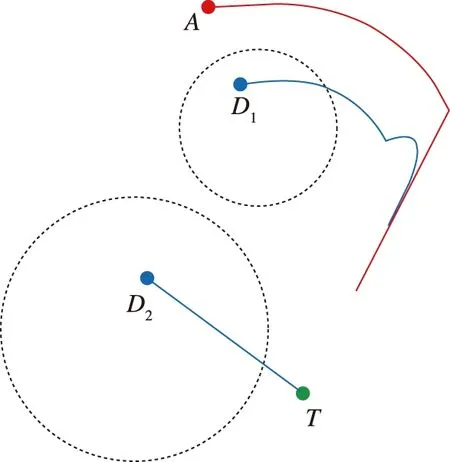

图9 D2直接与目标会合，D1拦截攻击方AFig.9 Defender turns directly with the target

2.2 生成决策树模型

决策树分类模型依据分类指标进行划分，由根到叶的顺序进行划分，包含一个根节点、若干个内部节点和叶节点。

对抗开始时，根据多防御方目标攻防问题的初始态势，将不同的初始态势进行分类特征值得计算，具体如下

(13)

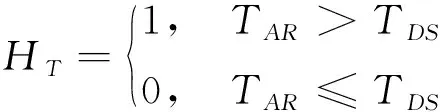
(14)

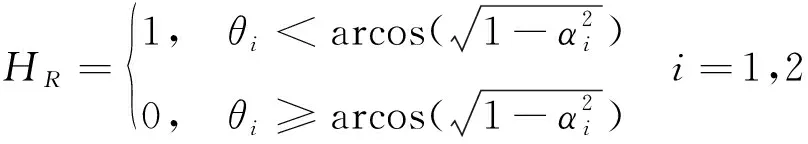
(15)

式中，

H

代表初始时刻目标

T

是否在Apollonius圆内；

H

代表初始时刻

T

>

T

是否成立，其中

T

表示某一防御方计算其直接与目标会合时需要的时间，

T

表示另一防御方计算单独拖延攻击方时攻击方能够打击到目标的时间；

H

表示初始时刻攻击方与目标之间是否被Apollonius圆挡住。

决策树模型的构建需要通过一定数量的训练样本进行训练。样本集合通过随机选取不同的初始坐标位置，确定不同初始位置时的攻防双方策略组合而获得，训练样本中包含初始状态参量、分类特征值、分类标签，训练样本如表1所示。

表1 训练样本集合

决策树分类算法中ID3算法依据信息增益作为测试属性选择标准来构造决策树。信息增益的计算如下

Gain

(

A

,

S

)=

Info

(

S

)-

Info

(

A

,

S

)

(16)

式中，

A

为某个属性，

S

为整个样本集合。

Info

(

S

)表示确定

S

中一个元素的类别所需要的信息量，

Info

(

A

,

S

)表示在已知属性

A

的取值后，确定

S

中一个元素的类别所需的信息量。其定义分别如下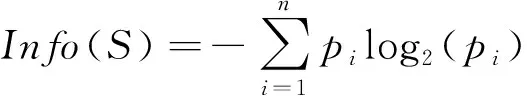

(17)

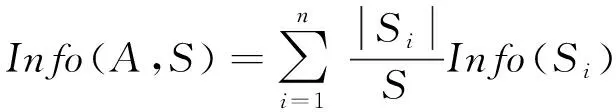
(18)

式中，

p

为样本集合

S

中第

i

类样本所占比例，|

S

|是子集

S

的记录个数。

对样本集合进行信息增益计算，每轮计算都选出信息增益最高的作为测试属性，如图10所示，直到样本集中所有分类都被完全分好为止。

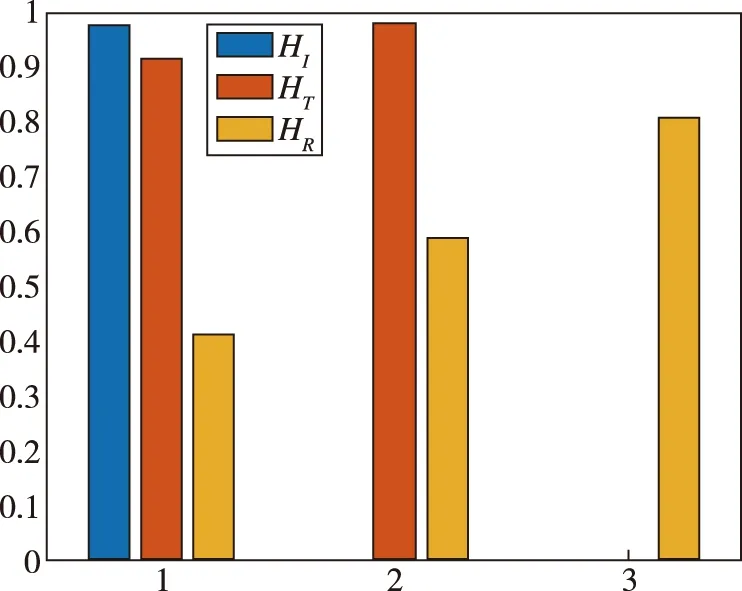
图10 每次各属性的信息增益计算Fig.10 Information gain calculation for each attribute each time

由图10可知，第1轮对3个属性分别计算其信息增益，最大值的是

Gain

(,

S

)=0

.

98，所以首先选择作为测试属性。以此类推，第2轮中

Gain

(,

S

)=0

.

98，第3轮中

Gain

(,

S

)=0

.

81，经过3轮计算分类后，所有的样本都完全分类。

由此得到决策树各轮的测试属性，用来生成最终的决策树模型。得到的决策树模型如图11所示。

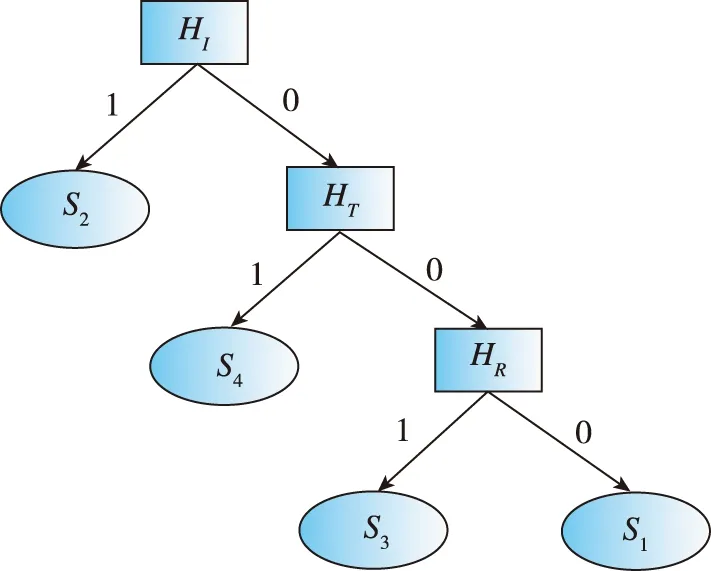
图11 决策树模型Fig.11 Decision tree model

3 举例决策树模型的应用

例1 防御方协同配合

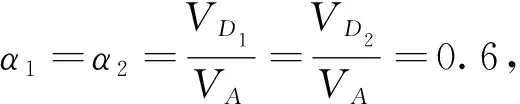
表2 例1的数据集

目标点位于

T

(0,-3)。攻击方所携带的燃料只允许其飞行400 s。1)第一步，按照决策树模型依次进行决策。首先计算目标

T

是否位于某一个Apollonius圆内。通过初始状态攻击方和防御方的位置和速度比值关系可以得到攻击方与两个防御方的Apollonius圆方程。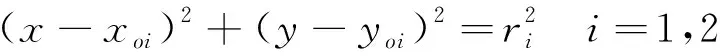

(19)

(20)

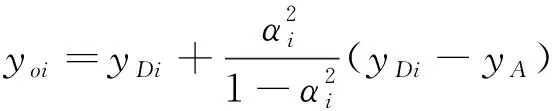
(21)

通过计算可知

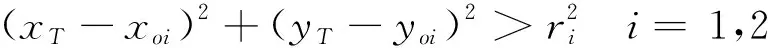
(22)

所以

H

=0。

根据决策树模型，此时已经将结果分类出来了，在该例子中给定的初始状态下，分类结果是

S

，防御方采取让两个Apollonius圆相切围堵攻击方进攻路线的策略。仿真模拟结果如图12所示。初始时刻，

D

位于整个战场的左边，距离目标较远。并且如果只有攻击方

A

和一个防御方

D

时，目标完全暴露在攻击方的视线之内，攻击方只要采取直线朝向目标进攻即可打击到目标获得胜利。

D

位于攻击方

A

和目标

T

之间，并且其Apollonius圆挡住了攻击方的视线。同样，如果只有攻击方

A

和一个防御方

D

，攻击方也可采取迂回策略打击到目标点获得胜利。所以，任何一个防御方单独与攻击方对抗都无法获胜。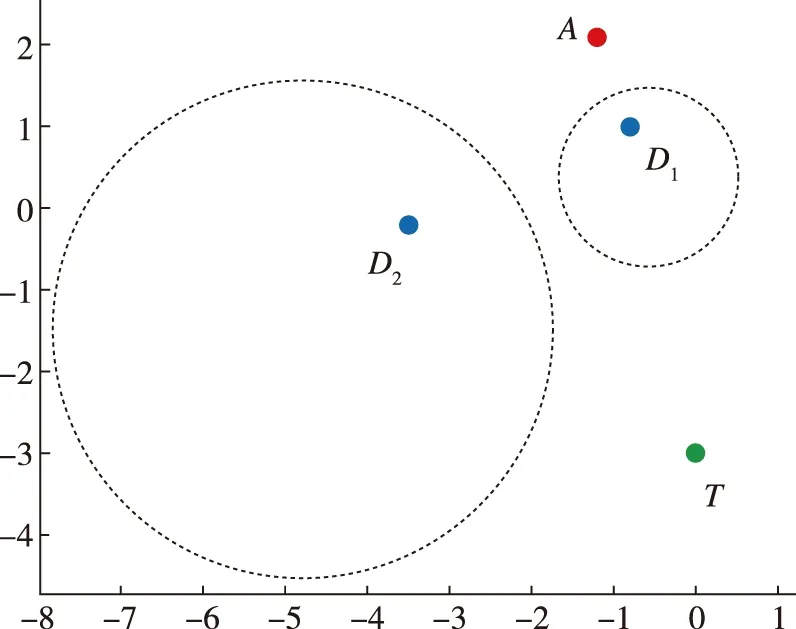

(a) t=0 s

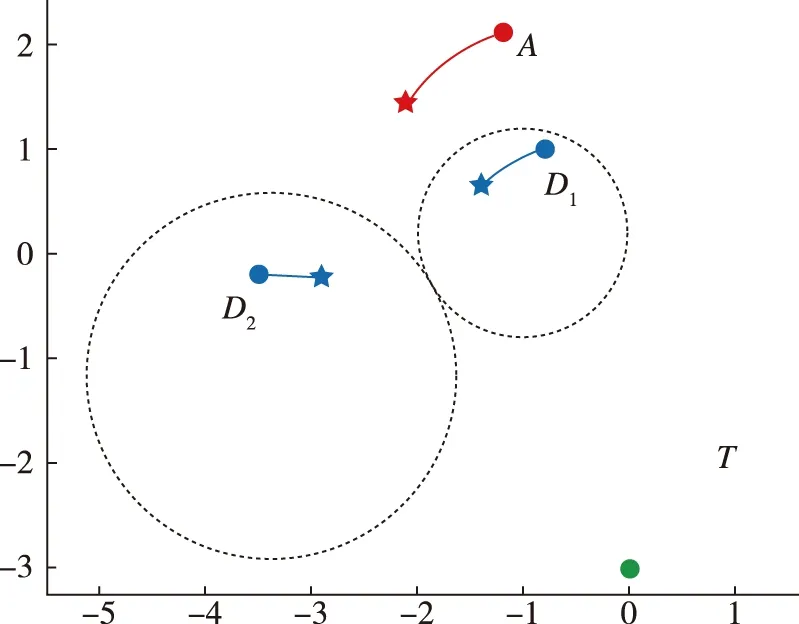
(b) t=58.5 s

(c) t=400 s图12 防御方实施合作策略Fig.12 Defenders implement cooperative strategy

两个防御方通过协作达到图12(b)状态，在(b)处，新的两个Apollonius圆相切。攻击方此时无法再继续通过穿越两个防御方之间来打击目标点的方式取得胜利，必须重新规划新的攻击路线。防御方通过相切的方式，延长了攻击方的飞行时间，使得攻击方无法在燃料耗尽前打击到目标。

例2 目标位于

Apollonius

圆内

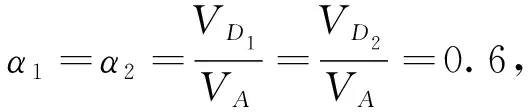
表3 例2的数据集

同样按照决策树模型的测试顺序。首先计算

H

，很容易得到

(23)

所以初始时刻，目标位于

AD

的Apollonius圆内，故

H

=1。该例的初始状态下，分类结果是

S

。

D

只要采取直线朝向目标的策略即可获胜，不管攻击方采取何种策略都无法改变。仿真结果如图13所示。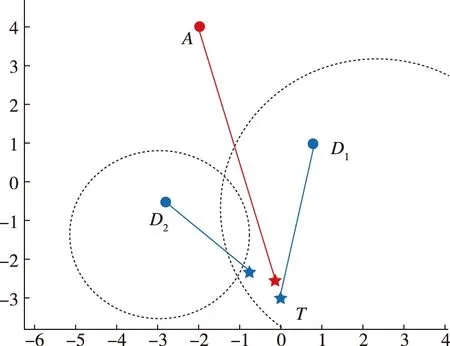

图13 D1直接与T会合Fig.13 D1rendezvous directly with T

事实上，攻击方在一开始就意识到已经不可能获胜了，它只能朝着距离目标最近的点前进，以期对目标造成该情形下的最大威胁和伤害。

4 总结与展望

本文以两个防御方的目标攻防问题为例讨论了决策树在多防御方目标攻防问题的应用。建立了问题的决策树模型，利用决策树思想与人们思考模式相近的优点，达到通过快速简单的判断得出多防御方目标攻防问题中各方的决策策略。主要结论如下：

1)提出了一种多防御方目标攻防对抗问题中多个防御方之间的合作方式。使攻击方、防御方Apollonius圆相切能够有效地阻止攻击方按照原先的路线进攻，迫使攻击方重新规划路线。并且利用平行四边形法则得到受多个防御方影响后攻击方的运动，利用了基于距离威胁的权重函数对平行四边形法则进行加权计算。

2)利用决策树的思想对多防御方目标攻防问题分类并决策。通过对每个候选测试属性信息增益的计算，建立了适用于多个防御方目标攻防问题下的决策树模型。

本文以两个防御方作为背景说明决策树思想在目标攻防问题上的应用，对于具有更多防御方的对抗场景，其合作方式也会变得比较复杂，因此还需要在更多防御方之间的合作方式上再进行更多的研究,但是决策树模型的思路大体上是一致的。