符号网络中融合聚集系数与符号影响力的链路预测算法

刘苗苗， 扈庆翠， 郭景峰， 陈 晶

(1.东北石油大学计算机与信息技术学院， 大庆 163318； 2. 燕山大学信息科学与工程学院， 秦皇岛 066004；3.黑龙江省石油大数据与智能分析重点实验室， 大庆 163318)

1 引 言

随着人工智能和机器学习技术的快速发展，涌现了许多社会媒体网络平台，随之也产生了大量复杂多样的网络大数据，对这些数据的表征和预测逐渐成为社会网络分析领域的研究热点.在现实网络中，实体间通常具有正负两方面的关系.例如，社会领域的人与人之间存在朋友和敌人关系，信息领域的用户间在观点上存在支持和反对关系，生物领域的细胞之间存在促进和抑制关系.这种同时具有正负关系的网络称为符号社会网络，简称符号网络[1].它与传统无符号网络的区别在于节点间是否存在链接的正负符号属性.符号网络是一种包含正负对立关系的二维网络，这种对立关系包括朋友、支持、喜欢等积极关系和敌人、反对、厌恶等消极关系.

符号网络是社会网络的重要分支，因其更贴近现实世界的特性，从而受到学术界的广泛关注.有关符号网络的研究主要集中在其结构分析，其中一个研究热点便是链路预测[2].它通过对观察到的网络结构进行分析来预测未知的链接，包括对未知链接建立的可能性预测、未知链接的符号预测以及对已观测到的链接缺失的符号类型的预测[3].符号网络链路预测在社会与信息领域的推荐系统以及知识图谱中实体间关系的学习中有着广泛的应用，在生物领域蛋白质相互作用关系的发现方面更是有着实际的意义和价值，可帮助指导实验过程，在节省时间和成本的同时提高预测准确率.

目前，针对符号网络的链路预测研究主要有基于节点相似性、基于概率统计的矩阵分解或填充以及基于机器学习等方法.第一类方法主要结合结构平衡理论，利用符号网络的局部或全局信息如节点的度、共同邻居数量、路径特征等设计相似性指标，代表性研究成果有：文献[4]提出基于结构平衡理论与网络局部特征的符号预测算法.文献[5]利用路径上传输节点相似度以及拉普拉斯聚类算法实现了符号网络的链路预测及推荐.文献[6]在基于节点共同邻居的符号预测算法CN-Predict的基础上，融合符号密度提出改进后的ICN-Predict算法，能够较好地实现符号预测，但该方法针对负链接的预测效果欠佳.文献[7]提取结构平衡环的局部特征以及频繁子图出现的次数构建特征来进行符号预测，但时间复杂度较高.文献[8]结合局部路径指标以及结构平衡理论对符号网络链路预测方法进行了研究.文献[9]提出一种符合结构平衡理论的高度对称四边形结构，基于局部结构的统计特性提取节点对的相似性、相异性以及反映节点对正负态度倾向的构造特征，在此基础上完成了符号预测.文献[10]融合结构平衡理论与节点的局部和路径结构相似性提出了一种符号网络边值预测算法PSNBS.文献[11]以结构平衡理论为基础，将Katz指标与网络拓扑相融合，提出一种符号预测算法.文献[12]考虑到负链接在符号网络中的重要性，融合结构平衡理论和地位理论提出基于隐空间映射矩阵的符号网络链接预测算法，在Epinions和Slashdot数据集上获得了较好的效果.针对符号网络拓扑结构中的非确定性因素，文献[13]利用集对理论，融合网络中的确定和不确定关系以及局部和全局信息实现了符号预测.总体而言，基于节点相似性的链路预测算法简单快捷，且通常能达到较高的预测准确率，但针对稀疏网络及负链接的预测效果往往欠佳.第二类算法主要通过将符号网络转化为矩阵，利用信任传播模型、矩阵分解或填充来完成符号预测，代表性研究成果有：文献[14]首次提出将符号预测问题转化为低秩矩阵分解和填充问题，先将n×n矩阵分解为n×k和k×n矩阵的乘积，再通过逐点误差来测量结果矩阵和原矩阵间的误差，最终达到了较好的符号预测效果.文献[15]在矩阵分解损失函数中运用了成对经验误差并引入了拉格朗日乘子，通过随机梯度下降算法求解符号预测结果.文献[16]提出带偏置的低秩矩阵分解模型，将邻居节点的出边和入边符号作为偏置信息引入模型，提高了符号预测精度.文献[17]提出一种基于投影非负矩阵分解的框架，通过嵌入网络结构和用户属性的无监督学习实现了负链接预测.针对大型符号网络的链路预测，文献[18]提出基于异步的分布式随机梯度下降算法的矩阵分解模型，在大大降低参数空间大小的同时提高了计算效率.总体而言，基于矩阵处理的符号预测方法计算复杂度较高，且模型评价难度大，因此限制了此类方法在大型网络中的实际应用.近几年，相关学者利用深度学习机制对基于卷积神经网络、循环神经网络等的链接表示与预测方法也进行了研究[19]，利用节点间的局部拓扑结构构建有序节点序列，并使用节点向量表达生成潜在链接的矩阵表示[20]，最后基于神经网络运算提取节点序列中节点对的多层隐含关系，实现链路预测[21].但此类算法大多关注的是传统社会网络中链接建立的可能性研究，针对符号网络中的链接与符号预测的研究相对较少.

综上所述，针对符号网络中的链接预测与符号预测双重目标，如何有效挖掘网络图的局部与全局特征，在保证算法效率的前提下提高预测的正确性，尤其是负链接以及拓扑结构特殊的符号网络的预测，是一个值得思考的问题.基于此，本文在考虑连接两节点的路径(包括路径长度及数量)、路径上的中间节点(包括一阶和二阶邻居节点的数量、度数)以及连边符号等信息的基础上，综合引入共同邻居节点的聚集系数以及基于结构平衡环的符号影响力的概念定义两节点的相似性.该方法能更全面地捕获符号网络的拓扑结构特征对于两节点间的链接建立的可能性以及符号类型的影响程度，既能保证算法执行效率，又能提高预测的准确性.本文在多个经典符号网络数据集上对所提方法进行了验证，实验结果也表明了该方法对于常规和稀疏的大型符号网络，以及拓扑结构特殊的小型网络的链接预测以及符号预测的有效性和更高的预测准确性.

2 预备知识

根据节点间的链接是否带方向，可将符号网络分为有向和无向符号网络，本文关注无向符号网络中的链路预测研究.一个无向符号网络通常被形式化表示为G=(V，E，S)，其中，V={v1，v2，…，vn}表示节点集，E={e(i，j)|vi，vj∈V，i≠j}表示边集，S={sign(i，j)|vi，vj∈V，i≠j}表示符号集合，取值如下.

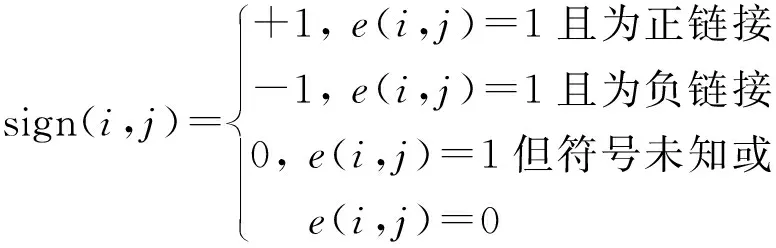
2.1 结构平衡理论

Heider[22]源于社会心理学提出的用户间结构关系的平衡模型为无向符号网络的结构分析提供了理论基础，它最初是针对三角形的平衡性分析开始，如图1所示.根据该理论，若无向符号网络中一个闭合环上所有边的符号之积为正，则该环为结构平衡环，否则为非平衡环.众多研究者在社会媒体网站中的实证研究表明，真实网络中平衡的三元环数目远大于不平衡的三元环数目，且随时间推移平衡三元环所占的比例日益增加[23]，像Epinions和Slashdot这类大型符号网络的平衡指数分别达到了89.6%和86.2%[24].2010年，Leskovec等[4]首次将结构平衡理论应用于符号预测问题.目前，该理论的一些基本规律已被广泛应用于符号网络链路预测算法研究[25].针对符号网络的预测研究，一方面要分析未知链接或缺失符号的已有链接的符号属性，即符号预测.通常依据结构平衡理论，力图使两个目标节点所在的环能最大限度地增强网络的结构平衡性.

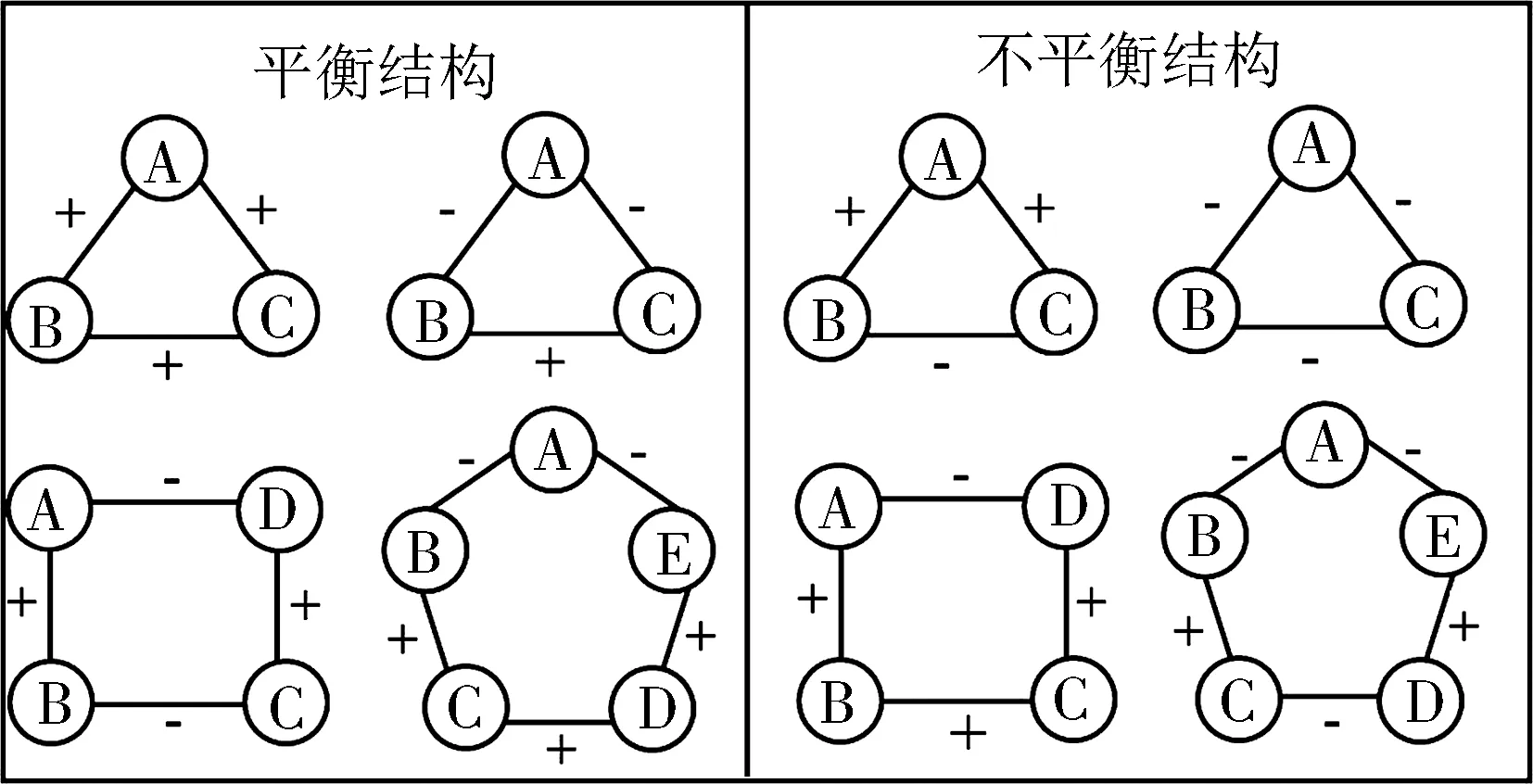
图1 结构平衡理论示意图Fig.1 Sketch of structural balance theory

2.2 经典的相似性指标

针对符号网络的预测研究，除了完成符号预测之外，还要分析两个尚未相连的节点间存在或建立链接的可能性，即链接预测.通常认为两节点间相似性越高，两者存在或建立链接的可能性越大.总体而言，经典的相似性指标有CN、Jaccard、AA、LP、Katz等，如下式所示.

(1)

(2)

(3)

(4)

β2(A2)xy+β3(A3)xy+…

(5)

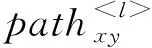
2.3 预测准确度评价方法

衡量链路预测算法准确性的基本方法是，给网络图对应的全集U中所有没有连边的节点对按其建立链接的可能性赋予一个分数值Sxy，然后根据实际网络的演化情况观察哪些节点对之间出现了新的连边，并与预测结果进行比较以判断预测的准确性.然而，社会网络的动态性使得实验中无法预知或观察到连边何时会出现，故而无法将预测结果与网络真实演化结果进行比较.因此，许多链路预测研究均以网络在某个时刻的瞬时快照为研究对象.针对传统无符号网络的静态快照的链路预测方法，常用的预测准确度的评价指标有AUC和Precision[26].实验中，为衡量算法预测结果的准确性，需将已知的边集E划分为训练集Etr和测试集Ete.通常采用K折交叉验证法[27]进行划分，每次取其中一个子集作为Etr，其余K-1个子集形成Ete.大量实验表明，十折交叉验证在计算量和性能间达到了最好的折中[28]即，针对每个数据集独立进行10次划分，保证每次划分中Etr∪Ete=E且Etr∩Ete=Φ且|Etr|=9|Ete|.

2.3.1 链接预测准确率评价指标AUC′ 针对符号网络中的链接预测，本文所提算法计算所得两节点间总相似度有正有负，其绝对值代表了两节点存在或建立链接的概率，其正负代表了被预测链接的符号类型.故而，本文对AUC[26]进行调整得到新的指标AUC′，如式(6)所示.

(6)

2.3.2 符号预测准确率评价指标Precision′ 针对符号网络中的符号预测，每次随机从测试集中取一条边作为待测边，假定其不存在，之后基于算法计算得到待测边的符号预测结果，并与真实的符号类型进行比较，以此评价符号预测准确性，相应的指标有TP、FP、TN、FN、TPR(又称Recall)、TNR(又称specificity)、Precision、Accuracy、F1-score等[29].符号网络的符号预测需评价正负符号预测准确性的综合指数，相关研究显示[12，17，30]，绝大多数真实符号网络中正链接数与负链接数的比值超过4∶1，也即实验中选取的待测边是正链接的概率远高于负链接.故而，本文实验中融合上述指标进行调整，为正链接的符号预测结果赋予权重1，为负链接的符号预测结果赋予权重0.5，得到调整后的指标Precision′，用于综合评价符号预测准确性，其定义如式(7)所示.

(7)

3 融合聚集系数与符号影响力的链路预测方法

在考虑符号网络的局部拓扑信息时，CN、RA、AA指标没有考虑到待测节点对的共同邻居节点的聚集系数对于两者的相似性影响.如图2，对于节点对而言，图2(a)和(b)中节点X与Y的度数、两者的共同邻居数目以及共同邻居的度数都相同，且共同邻居节点B的聚集系数也相同，但共同邻居节点A的聚集系数不同.显然，图2(b)中共同邻居节点A对于节点对的相似性贡献更大.针对该情况，综合引入共同邻居聚集系数CNCC(Common Neighbor Clustering Coefficient)全面衡量两节点的共同邻居的属性特征对于两者的相似性贡献.此外，对真实符号网络拓扑特征的相关研究显示，符号网络中正负链接的分布不均衡，且负链接具有更重要的作用.因此，在进行符号预测时，连接两节点的路径上正链接数目也远超过负链接数目，也即由于正负链接数目比例的不同，正负符号在结构平衡环中对于目标节点对的符号影响也不同.为此，引入符号影响力SI(Sign Influence)的概念，对多步长路径上的符号类型赋予不同的权重，以更精确地衡量多条路径对于两节点间所建链接的符号类型的影响程度.

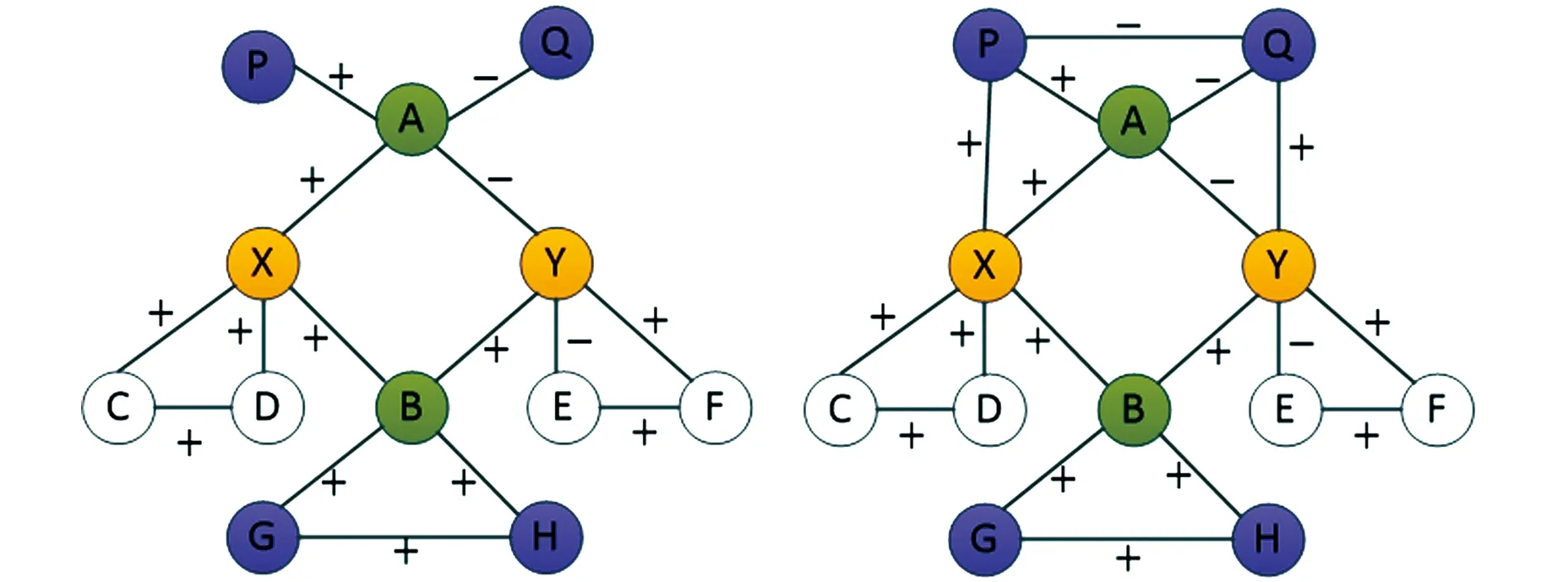
(a) (b)

基于以上思考，我们提出CNCC_SI算法.在考虑基于局部路径信息的三元环对节点的相似性影响时，引入共同邻居聚集系数，综合考虑两节点的度、共同邻居数目、共同邻居的度及聚集系数的贡献；在考虑基于全局路径信息的平衡环对节点的相似性影响时，引入符号影响力，综合考虑连接两节点的路径上中间传输节点的度数以及过渡链接的符号类型的贡献；考虑到高阶步长的路径信息计算复杂度较高，根据文献[31]和文献[32]的研究结果，本文研究中利用了连接两节点的步长为2和3的路径信息分别定义了节点对的二阶相似性和三阶相似性，以达到预测准确性和计算效率上较好的均衡.

3.1 相关定义

为描述方便，对变量及符号表示如表1.

表1 CNCC_SI算法相关变量定义及符号说明

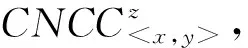
定义1共同邻居的聚集系数.

(8)

为提高预测准确率，CNCC_SI算法综合考虑两节点的度数、一阶共同邻居的度数和聚集系数、连边符号等局部结构特征对于两者的相似性影响.设G=，∀vx，vy∈V且sign(x，y)=0，基于结构平衡理论，定义节点对基于一阶共同邻居节点的相似性得分，记作SCN1，如式(9)所示.

定义2两节点基于一阶共同邻居的相似性得分.

(9)

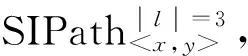
(10)

式(10)中，l=vxe(vx，vp)vpe(vp，vq)vy为连接vx与vy的长度为3的路径；vp和vq为路径l上的两个中间节点，即vp∈N1(x)∩N2(y)，vq∈N1(y)∩N2(x)；α代表路径l上正链接的权重，设为1；β代表路径l上负链接的权重，设为0.5.

定义3路径l基于平衡环的符号影响力.

基于上述定义，利用连接两节点的步长为3的路径信息定义两节点基于二阶共同邻居的相似性得分，记作SCN2，如式(11)所示.

定义4两节点基于二阶共同邻居的相似性得分.

(11)

将不相连的两节点间的总相似度定义为两节点基于一阶共同邻居和二阶共同邻居的相似性得分之和，记作SCN(x，y)，如式(12)所示.|SCN(x，y)|代表节点vx与vy建立链接的可能性大小，链接的符号类型与SCN(x，y)的符号类型相同.

定义5节点对总相似性得分.

SCN1(x,y)+SCN2(x,y)

(12)

3.2 算法实现

Algorithm： CNCC_SI

Input：G=(V，E，S)

Output： SCN(x，y) and sign(x，y)

Begin

1) Read Dataset File

2) For eachvx，vy∈Vdo

3) IFe(x，y)=0 ore(x，y)=1∧sign(x，y)=0

4) {Find all paths where |l|=2， Calculate SCN1(x，y)

5) Find all paths where |l|=3， Calculate SCN2(x，y)

6) Calculate SCN(x，y)}

7) If {SCN(x，y)>0 then sign(x，y)=+1

8) Else sign(x，y)=-1}

9) Output sign(x，y)

10) Sort |SCN(x，y)| and get Topk

End

4 实验与分析

4.1 数据集

采用符号网络研究中常用的3个经典大规模真实数据集Epinions、Slashdot和Wikipedia，以及3个小型数据集进行实验，基本信息见表2.所选3个小型数据集拓扑结构(正负链接数的比例、节点的度分布特征等)都较为特殊，其中CRA和FEC是仿真数据集，Gahuku Gama Subtribes(记作GGS)是真实的符号网络数据集.

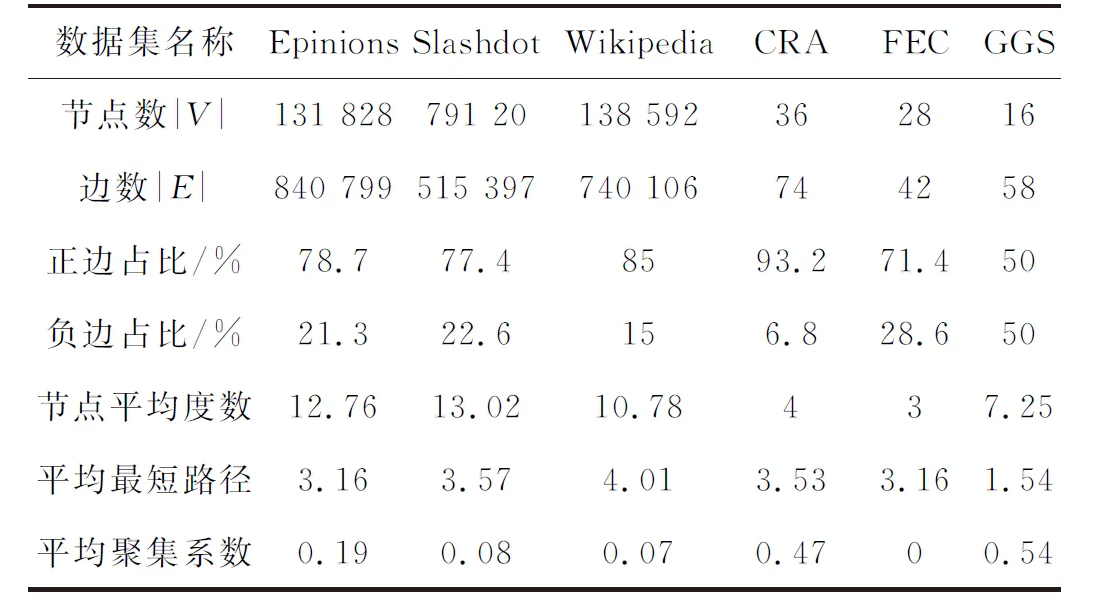
表2 数据集基本特征

4.2 实验结果及分析

针对符号网络中的符号预测，文献[6]中所述CN-Predict和改进后的ICN-Predict是经典的符号预测算法.针对符号网络中的边值预测(包括链接预测与符号预测)，PSNBS算法[10]是较为经典的算法.为衡量本文所提算法对符号网络链路预测的准确性，采用十折交叉法划分实验数据集，并以前文所述AUC’、Precision’等为评价指标，与上述3个经典算法分别进行了链接预测与符号预测准确性的实验对比.

4.2.1 基于AUC′的链接预测准确率实验结果 以AUC′为评价标准，将所提算法与PSNBS算法进行了链接预测准确性的对比分析，结果如图3所示，图中显示的是10次独立实验的平均值.且针对前5个数据集，图中显示的PSNBS实验结果为该算法中步长影响因子λ分别取0.6、0.9、0.8、0.9和0.8时所得到的算法的最高预测准确率.

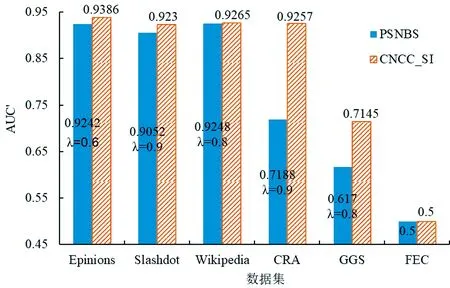
图3 基于AUC′指标的链接预测实验结果Fig.3 Link prediction results based on AUC′

从图3可清晰看出，本文所提算法在3个大型经典符号网络以及小型仿真网络CRA中均得到了较好的预测效果，链接预测准确率均高于PSNBS算法.尤其针对正负链接数目分布不均衡的小型网络CRA(接近14∶1)，所提算法链接预测准确率较PSNBS有较大幅度提升.

对于GGS网络，算法预测准确率相比前四个数据集相对较低.该网络描述了新几内亚高地16个子部落(节点)之间真实的政治联盟和对立关系，其拓扑结构较为特殊，如图4所示.16个子部落根据同盟与敌对关系形成了3个小的社区(团体)，同一社区内节点间都为正向的同盟关系，不同社区的节点间均为负向的对立关系，16个节点的度数以及聚集系数的分布情况分别如图5和图6所示，58条边中正负链接比例为1∶1.针对正负链接数量完全相同的小型数据集，CNCC_SI算法链接预测准确率仍可达到71%，具有较强的健壮性.

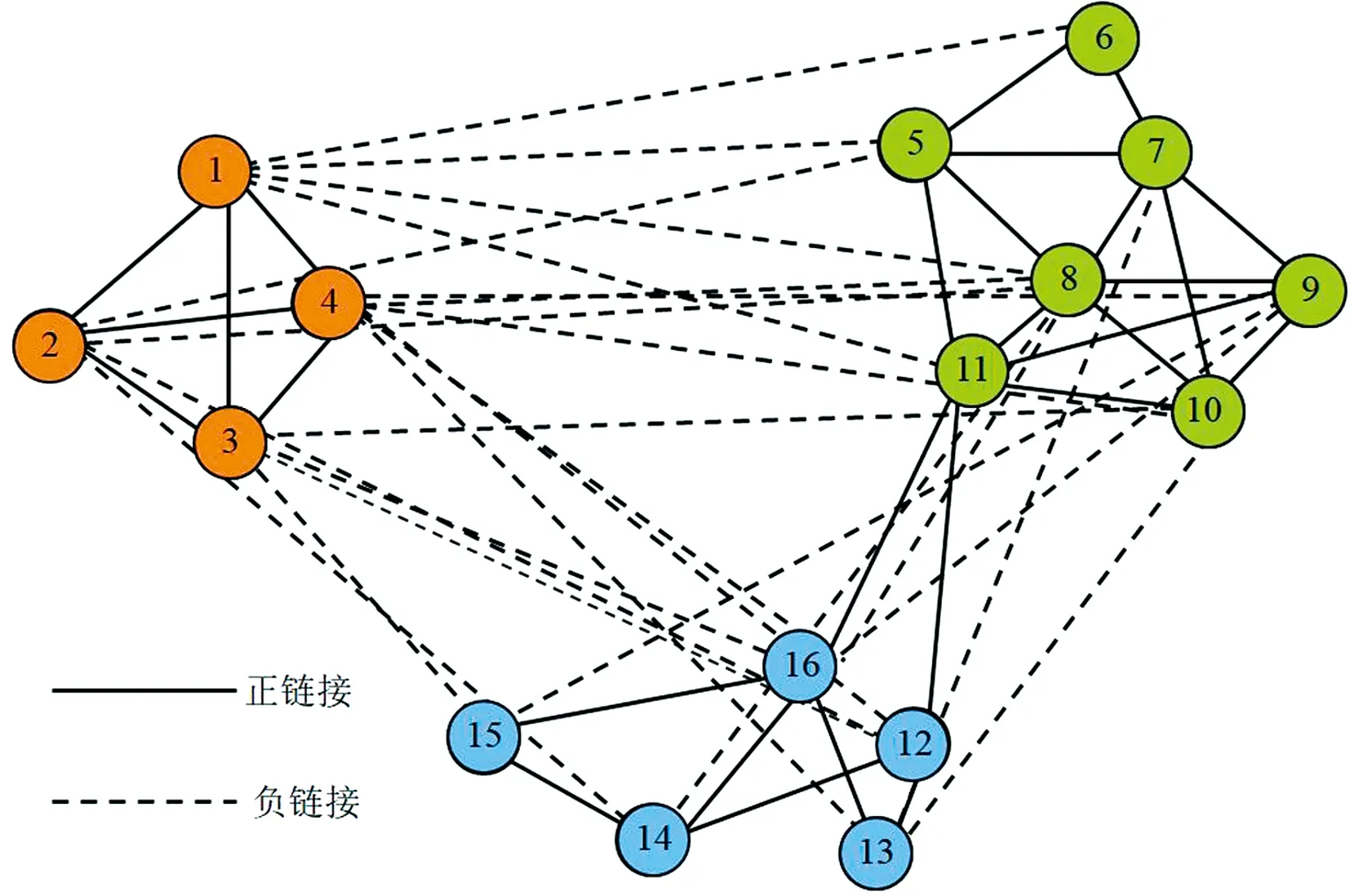
图4 GGS网络拓扑结构示意图Fig.4 Topology of GGS network

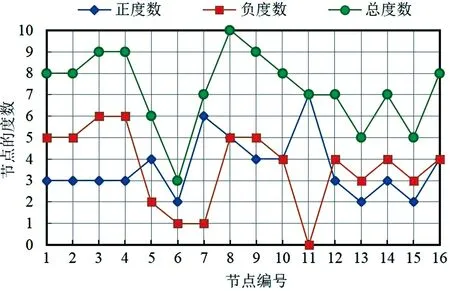
图5 GGS网络节点度数分布示意图Fig.5 Degree distribution of GGS network

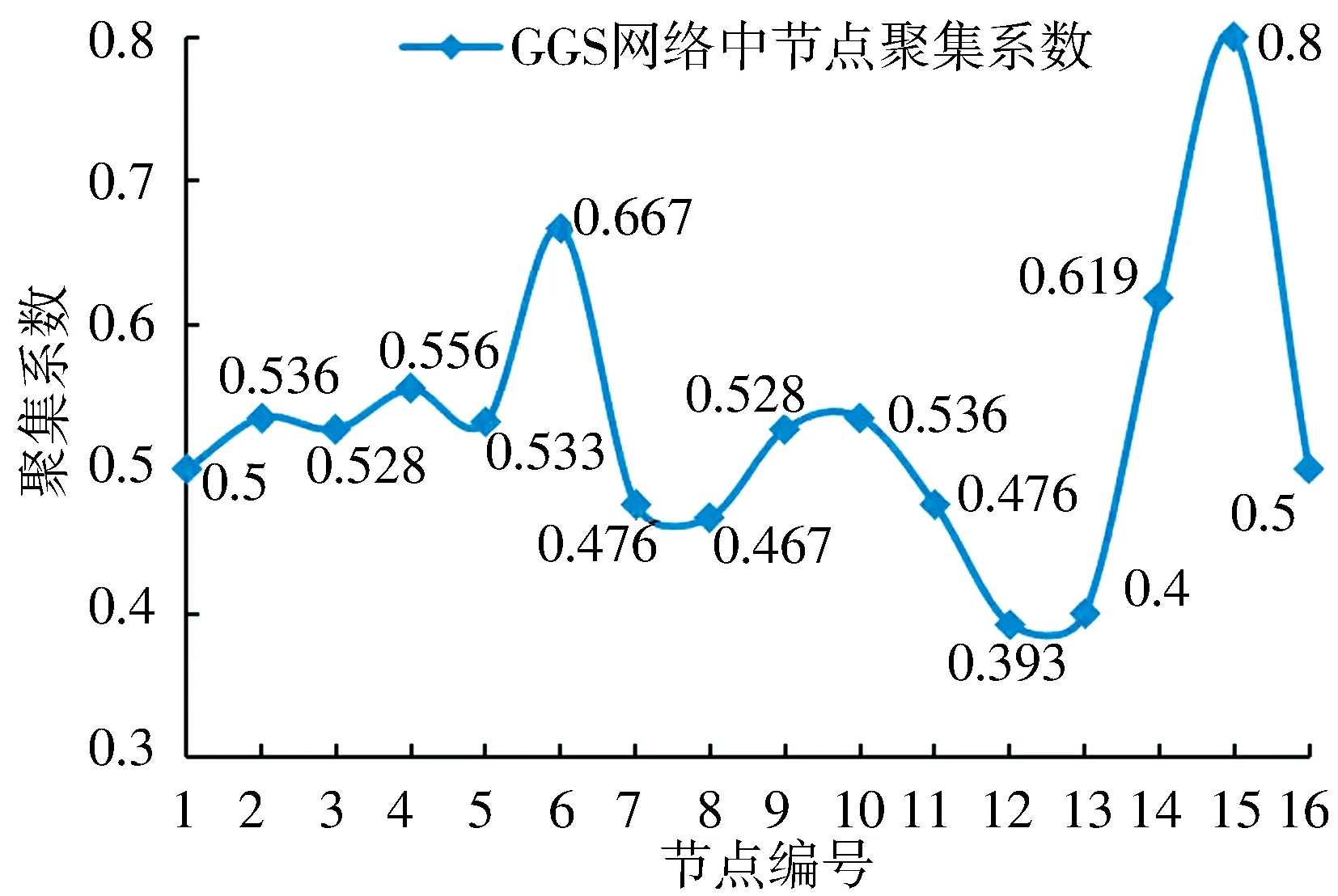
图6 GGS网络节点聚集系数分布示意图Fig.6 Clustering coefficient distribution of GGS

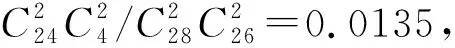
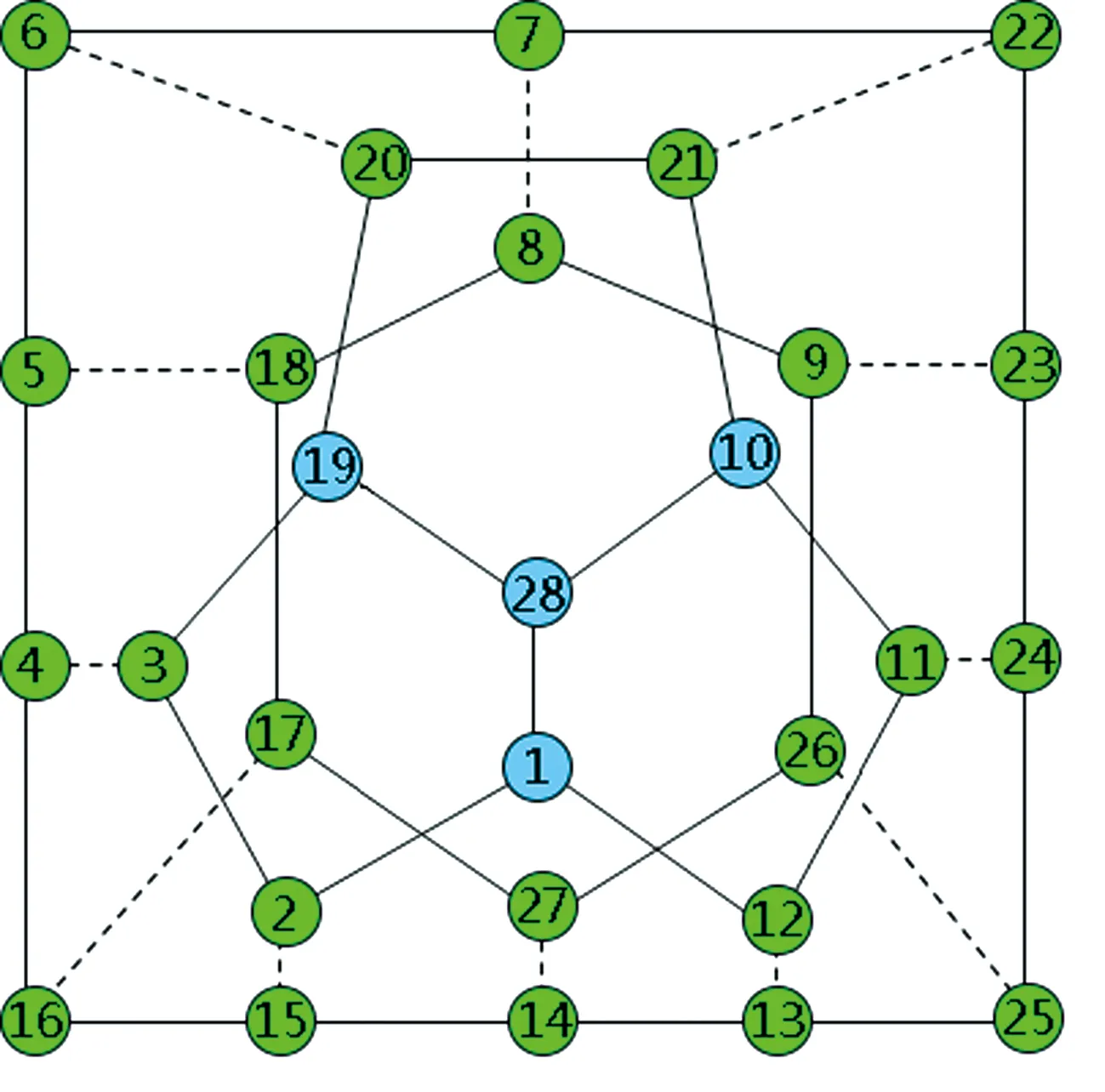
图7 FEC网络拓扑结构示意图Fig.7 Topology of FEC network

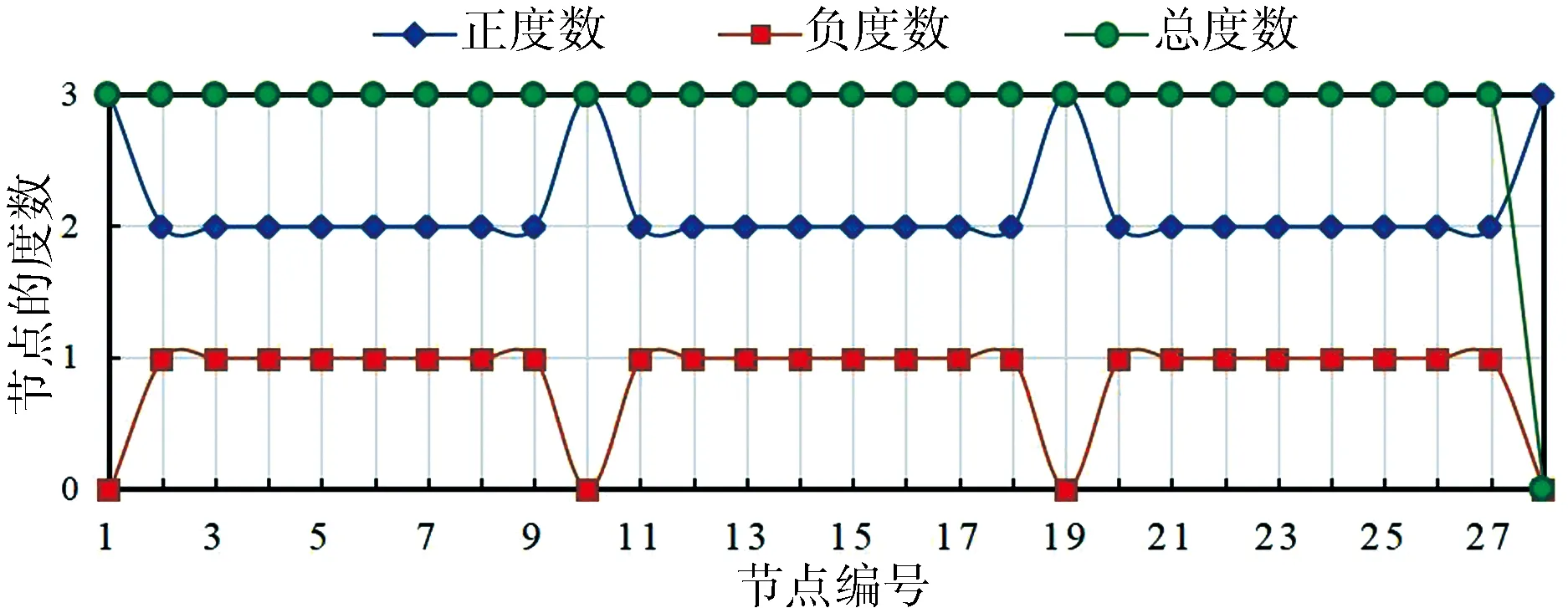
图8 FEC网络节点度数分布示意图Fig.8 Degree distribution of FEC network

4.2.2 基于Precision′的符号预测准确率实验结果 以Recall、Precison、F1-score、Accuracy等为评价指标，对CNCC_SI算法的符号预测准确性进行了验证，结果见表3所示.从表3可以看出，所提算法无论对于具有常规拓扑结构分布的大型真实符号网络，还是拓扑结构特殊的小型仿真及真实数据集，均达到了较好的符号预测性能，且针对负链接的预测准确率较高，具有良好的稳健性.

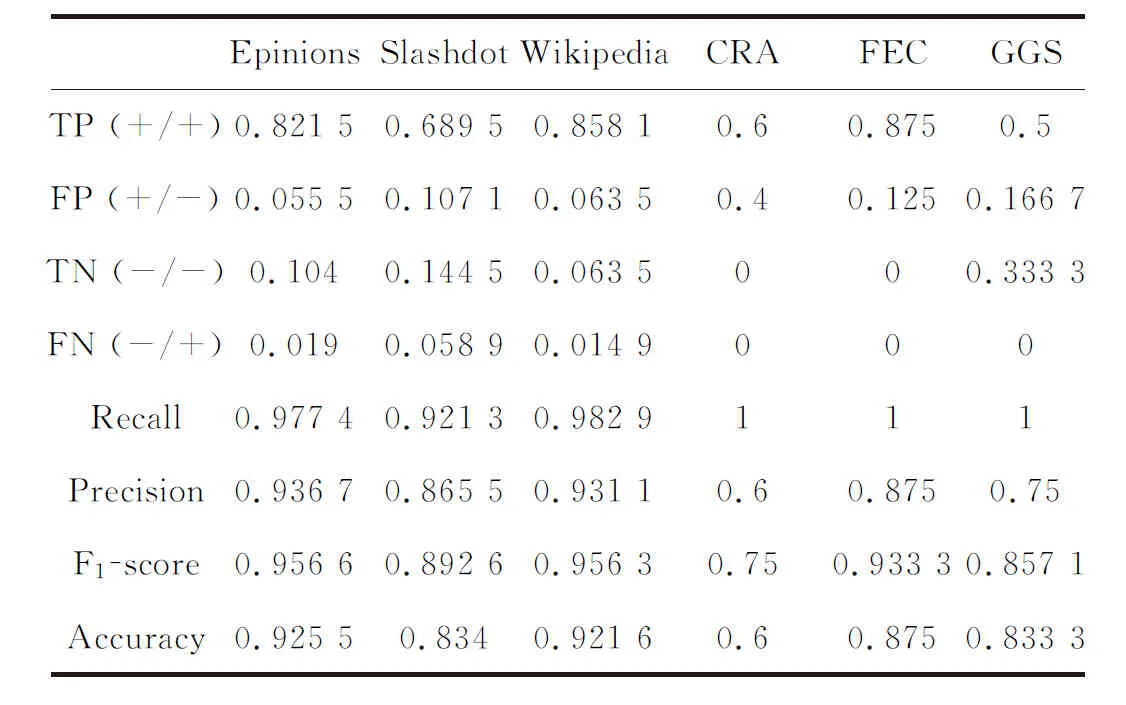
表3 CNCC_SI算法符号预测准确性实验结果

与此同时，以Precision′为评价标准，将所提算法与PSNBS算法进行了符号预测准确性的对比实验，结果如图9所示，图中显示的依然是10次独立实验的平均值.从图中可以看出，CNCC_SI算法在6个数据集上的符号预测准确性均高于PSNBS算法，总体获得了较好的符号预测性能.尤其针对3个拓扑结构特殊的小型符号网络，所提算法符号预测准确性均有较大幅度提升，进一步显示了CNCC_SI算法融合共同邻居聚集系数和符号影响力进行符号预测的正确性和有效性.

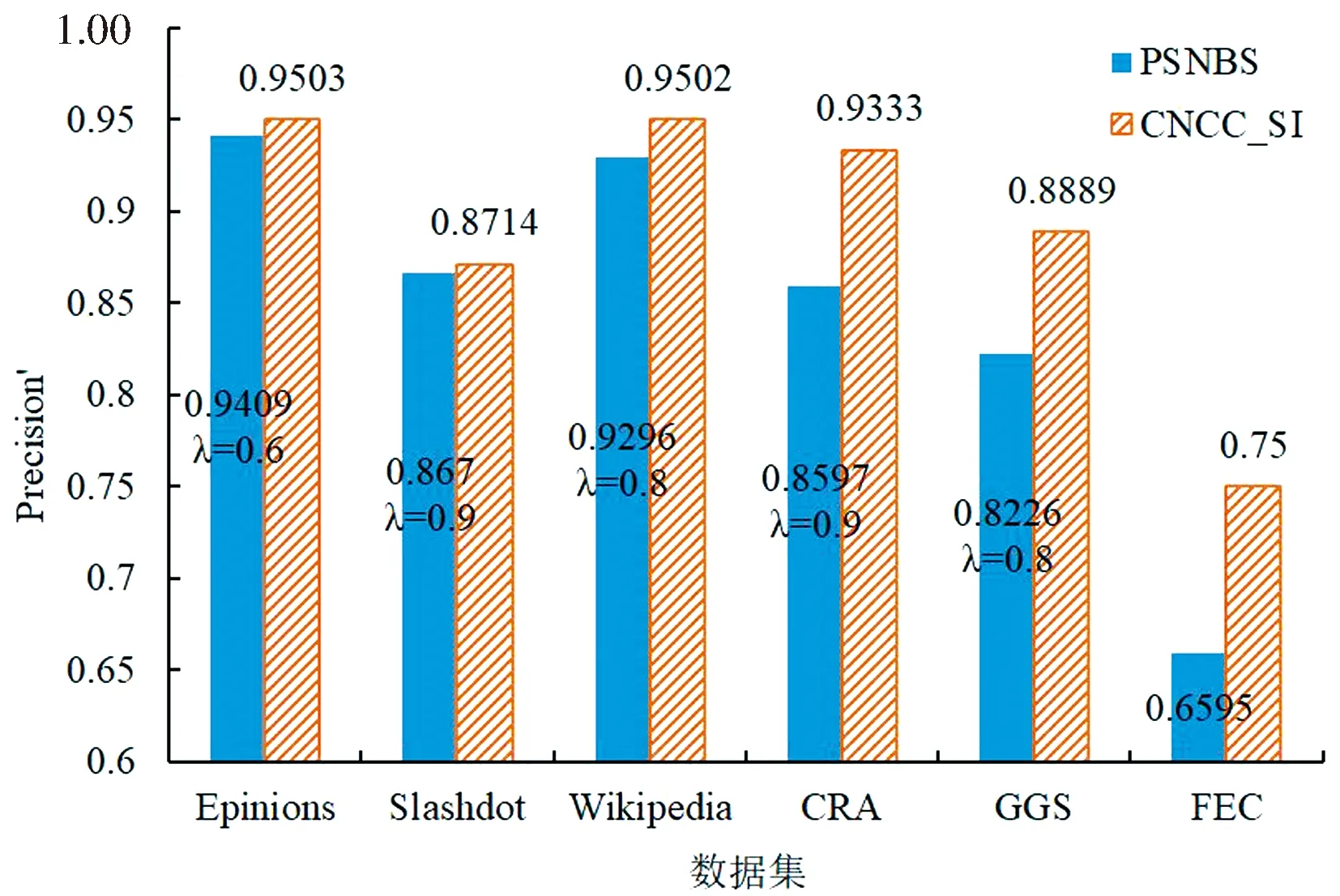
图9 基于Precision′的符号预测准确性实验结果Fig.9 Sign prediction results based on Precision′

4.2.3 可调步长参数敏感性分析 为达到预测准确性与计算复杂度上较好的均衡，本文算法将两节点基于一阶共同邻居的二步相似性得分和基于二阶共同邻居的三步相似性得分之和作为两节点的总相似度.然而，相关研究也已表明，相对于低阶路径而言，高阶路径对节点的相似性贡献相对较低，且针对不同拓扑结构的数据集，网络的平均最短路径也不尽相同.为此，许多基于路径结构信息的相似性计算方法为不同步长的路径赋予了可调步长参数，以区分高阶路径与低阶路径的相似性贡献程度.本文实验中，为连接两节点的步长为2和3的路径分别赋予了可调步长参数ε(0.5≤ε≤1)和1-ε，并进行了预测准确率的分析，将式(12)中两节点的总相似性得分修改为式(13)所示，记作SCN(x,y)ε，修改后的算法记作CNCC_SIε.

定义6融合步长影响因子的相似性得分.

SCN(x,y)ε=ε×SCN1(x,y)+

(1-ε)×SCN2(x,y)

(13)

基于式(13)，在相同的条件下进行了实验，可调步长参数ε分别取0.5、0.6、0.7、0.8、0.9和1，所提算法基于AUC′和Precision′评价指标的实验结果分别如图10和图11所示.

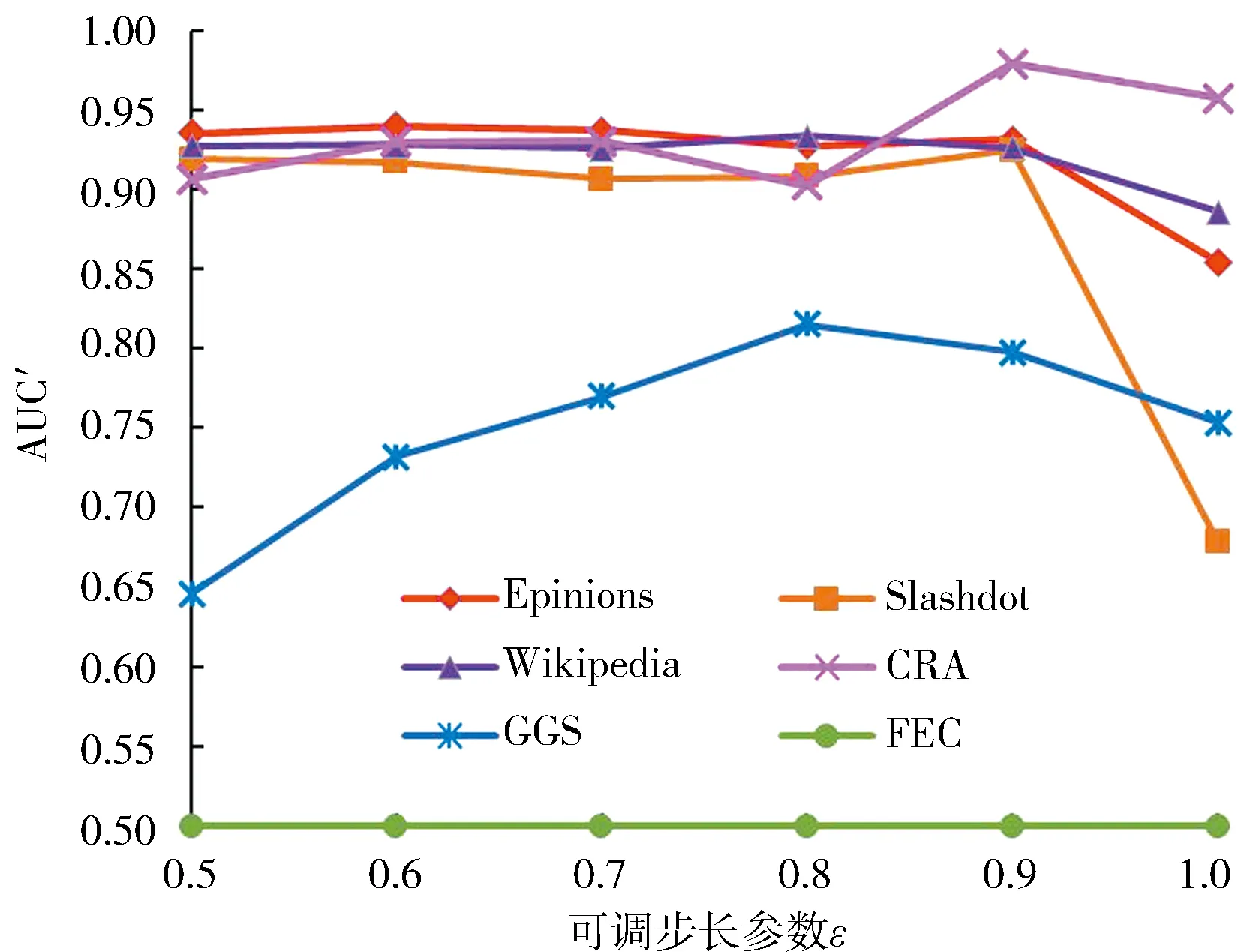
图10 CNCC_SIε算法基于AUC′的链接预测准确率Fig.10 Link prediction results of CNCC_SIε based on AUC′

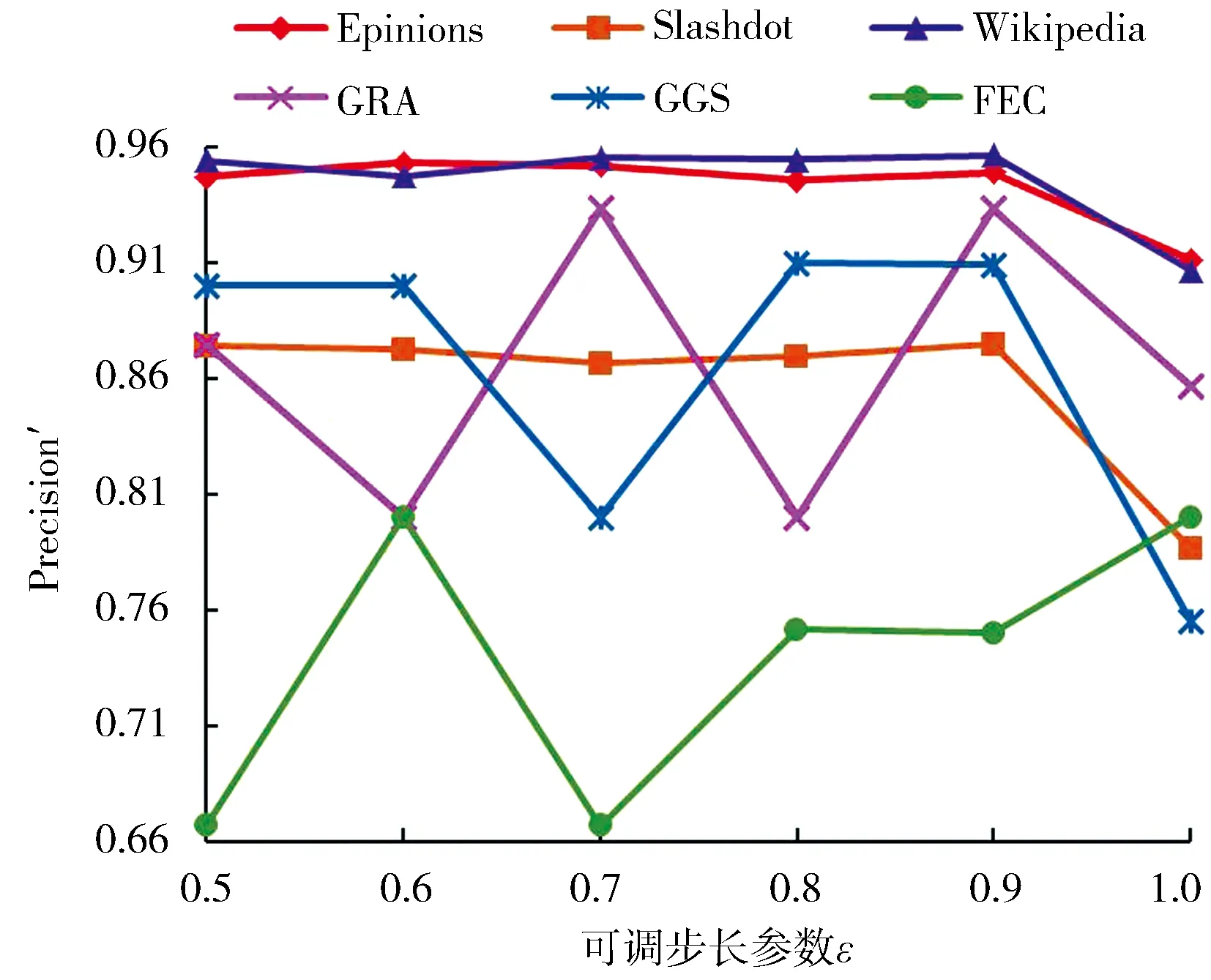
图11 CNCC_SIε算法基于Precision′的符号预测准确率Fig.11 Sign prediction results of CNCC_SIεbased on Precision′

从图10和图11可知，对于同一个网络，所提算法链接预测和符号预测准确率随ε的变化趋势是一致的.针对Epinions、Slashdot、Wikipedia、CRA和GGS网络，链接预测准确率和符号预测准确率都是在ε分别取0.6、0.9、0.8、0.9和0.8时达到了最高值，又一次验证了所提算法的正确性.

4.2.4 与其他算法预测准确率对比

(1) 基于AUC的符号预测准确率对比.为进一步验证本文所提算法的正确性和有效性，以文献[6]中的AUC为符号网络链路预测准确性的评价指标，将CN-Predict、ICN-Predict、PSNBS(λ)、CNCC_SI、CNCC_SIε算法进行了预测结果的对比，见图12.在此说明，文献[6]中AUC评价指标定义见式(14)所示，其中n代表被预测的链接对数，取值为10 000；n′代表符号预测结果中正链接预测正确的数量，权重为1；n″代表符号预测结果中负链接预测正确的数量，权重为0.5.

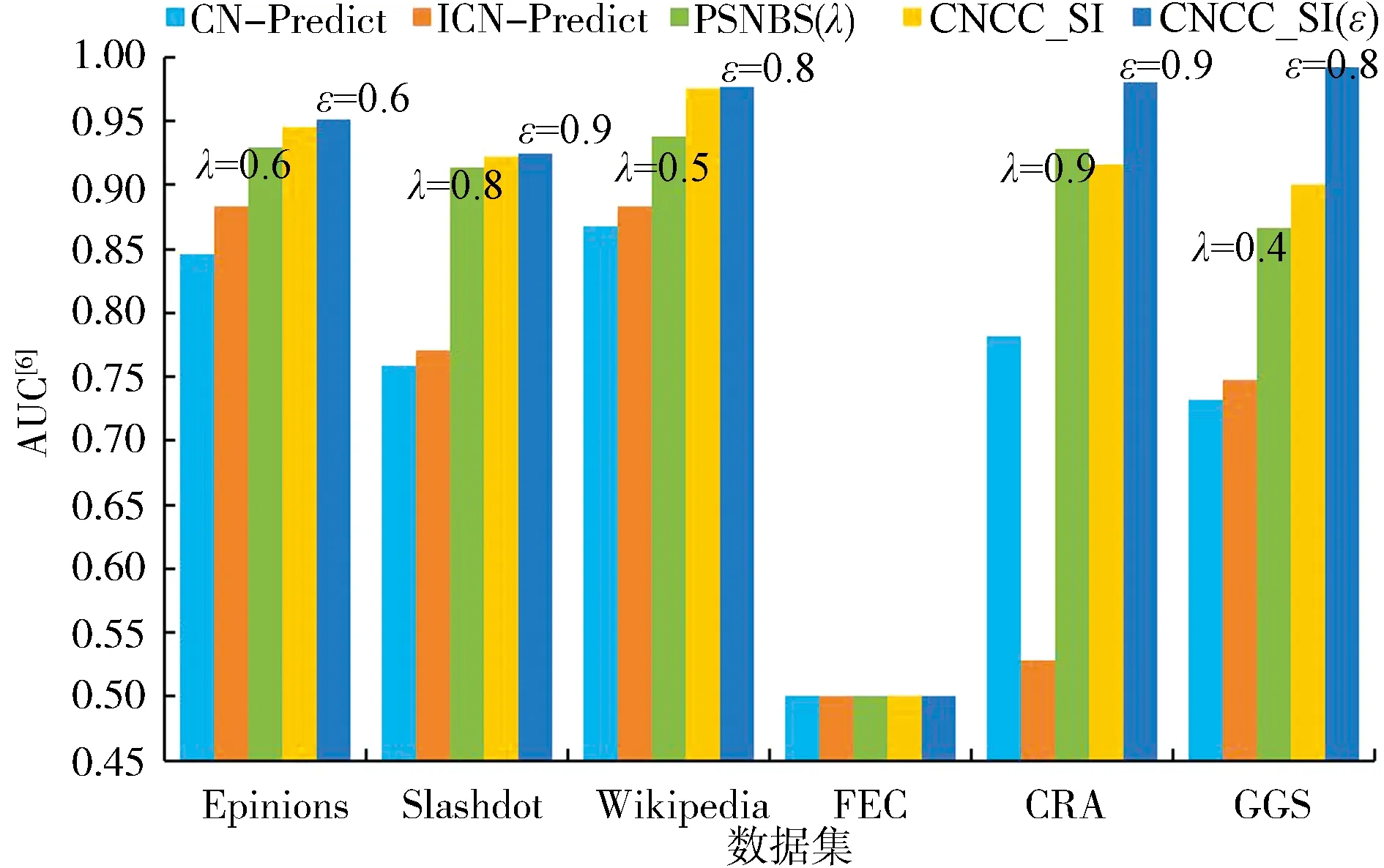
图12 基于AUC[6]指标的符号网络链路预测准确率对比Fig.12 Link prediction results comparison based on AUC[6]

(14)

实验结果显示，针对6个符号网络数据集，基于可调步长参数敏感性分析的CNCC_SIε算法预测准确率均高于其他算法，表明基于共同邻居聚类系数和符号影响力的相似性计算方法能有效解决其他算法(基于共同邻居的度、节点符号密度等)对某些拓扑结构特殊的网络存在的预测准确率较低的问题，具有更好的稳健性.

(2) 基于Accuracy的符号预测准确率对比.同样地，我们以Accuracy[29]作为符号预测准确率的评价指标，在3个大型数据集上进行了实验，将所提算法与已有的经典的符号预测算法进行了对比.例如，文献[33]所提基于谱分析的不平衡度量的符号预测方法MOI、文献[34]所提符号网络中基于高阶环监督学习的链路预测算法HOC、文献[35]所提将聚类之间的相对相似性定义应用于协同过滤算法的符号预测方法CF，文献[36]所提基于谱分析聚类的矩阵分解方法MF，以及文献[37]所述基于封闭三角结构的符号预测算法CTMS.以上7个算法在3个大型数据集上的实验结果如图13所示.

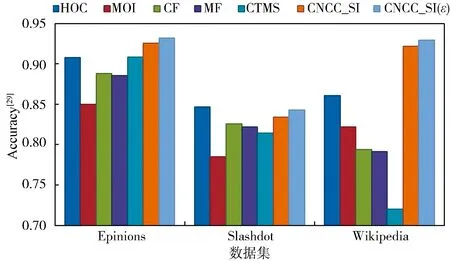
图13 基于Accuracy[29]的符号网络链路预测准确率对比Fig.13 Link prediction results comparison based on Accuracy[29]

从图13可知，MOI算法虽度量了符号网络中长度小于等于10的环的不平衡程度，但其符号预测准确率依然低于其他方法.CF算法较低的符号预测准确率也说明，进行符号预测时除考虑网络的结构平衡性以外，节点的局部和全局结构特征对符号预测结果的影响更大.HOC算法不仅学习了三元环的结构特征，同时还融入了四元环和五元环的结构特征，但符号预测效果总体上依然差于本文所提仅使用三元环和四元环的结构特征的CNCC_SI算法.上述实验结果再次显示，影响符号网络中连边符号的主要因素为边的两个端点的属性特征，其次是连边所处的局部结构特征和全局结构特征.此外，本文所提算法虽然在Epinions和Slashdot两个数据集上Accuracy指标(分别为93.2%和84.3%)略低于文献[9]所述SPR模型(分别为94.7%和93.8%)，但在Wikipedia数据集上预测正确率(92.9%)明显优于SPR算法(86.6%).且Accuracy指标并没有区分预测正确的样本是正例还是负例，因此针对拓扑结构特殊的数据集，相关算法预测效果欠佳.而本文所提算法能同时实现链接预测与符号预测双重目标，且关注了符号网络中正负链接的比例问题，针对各种拓扑结构的符号网络，总体而言均具有较好的预测性能.

4.3 算法复杂度分析

CNCC_SI算法使用邻接表储存图边关系，针对无向符号网络图G=(V，E，S)，节点数和边数分别为n和m，算法空间复杂度是O(m+n).算法在计算网络图中任意两节点基于一阶共同邻居的二步相似性得分时，计算复杂度为O(m2n)；算法在计算任意两节点基于二阶共同邻居的三步相似性得分时，时间复杂度为O(mn2).因而，算法总的时间复杂度为O(m2n).与其它几种算法相比，所提算法计算复杂度略微提高.例如，文献[9]所述SPR模型需遍历网络中的所有边，获取任意节点对相应的邻居节点并计算节点对的相似性-相异性，进行符号预测，算法的计算复杂度为O(m2)，其中，m为网络中的边数，为网络中节点的平均度数.针对大规模符号网络，本文所提算法计算复杂度虽略微增加，但在达到较高预测准确率的前提下，仍可保证时间上的可行性和有效性.

5 结 论

提出CNCC_SI算法，结合共同邻居节点聚类系数和符号影响力分别定义了两节点基于一阶共同邻居的二步相似性和基于二阶共同邻居的三步相似性，并通过可调步长影响因子的敏感性分析对算法做进一步改进，在多个数据集上的实验结果验证了所提算法对于符号网络链接预测和符号预测的正确性、较高的预测准确率和良好的稳健性.然而，针对具有复杂结构的符号网络(例如含时网络、多层网络、超网络等)中的链路预测，仍存在较多挑战.针对超大规模符号网络的动态性、网络中节点及其链接关系的不确定性等，如何有效利用多维的丰富信息进行快速、准确的链路预测，设计局域化或并行化算法等，都将是下一步的研究内容.