剖析中考试题，启迪深度教学

韩芳

摘要：在当前的中考教育环境下，习题的多样性和复杂性是许多学生面临的难点。中考试题有很强的代表性，能够将初中知识完美融合其中，全方位考查学生的知识掌握程度。对试题的详细解析能够有效地提升学生的思维能力，达到深度学习的目的[1]。

关键词：中考试题;深度教学

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2021）17-105

与小学数学不同，初中数学的知识较为复杂、专业性较强，有很多不能直观理解的公式和条件。很多学生不能适应这一阶段的学习，感觉学习难度较大，不能快速解答问题和正确使用公式定律。因此，初中数学教师在平时的教学活动中要尽可能地将所学新知与学生原有知识进行融合，寻求简洁高效的学习方式，使学生能够高效快速地解答问题。

一、引导学生运用数学化归思想，把复杂问题简单化

初中数学教师在教学时不能只讲解试题，要把一些数学思想和解题方式教授给学生，比如化归思想。老师要时刻强调用宏观的角度看待问题，认真分析如何将复杂的问题简单化，如何利用现行的知识点进行解答。学生进行全面的思考之后，能够意识到根本所在，潜移默化中培养学生的学习能力。

案例：某个题目给出少数的已知条件，要求学生计算一个不规则多边形的面积，并给出合理的解题思路。学生并没有学过复杂不规则多边形面积的计算方法，所以教师要引导学生用学过的知识进行解答，通过将不规则多边形转换为规则的三角形和长方形，这样，解题过程就变得简单了。又如，老师提问：“如果有一张图，分别是5个半径都为2的圆，圆心依次是a、b、c、d、e，那么，如何求解出图中所有扇形阴影区域的总面积？”很多同学看到题目后会觉得难度较大，如果用普通的方法求解，先把每个扇形的陰影面积求出来，然后相加，计算过程烦琐，难度较大，很容易出错[2]。如果使用化归思想，学生就会发现其中的规律，已知圆的半径，可以套用扇形的计算公式，求证出扇形所对圆心角的度数，就可以很容易计算出题目的答案。所以，数学化归思想的运用有利于学生利用较短的时间计算出更准确的答案。

二、利用中考试题进行课堂新知识教学，并结合实际生活达到深度学习的效果

案例：给出一道中考试题：已知点A（-2，0），B（2，0），动点M满足|MA|+|MB|=2，则点M的轨迹是（ ）。

A.椭圆 B.双曲线 C.线段 D.不存在

多数学生能够通过简单的计算获得正确答案，但是部分学生对相关的推理过程和公式没有真正理解，题目稍做改变，学生就是失去了判断力。对于以上问题，教师不能只进行简单的讲解，需要学生自主探讨如何改变题目以获得ABCD四种答案。由这一案例可以看出，在日常的课堂中，教师可以根据题目特点进行准确分析，设计不同的教学问题，给学生营造充实的教学环境和交流氛围。要达成这一点，要求教师要充分观察生活，把生活中的初中数学问题带到课堂上来，吸引学生主动进入教师创设的情境中，自由地学习和观察。同时教师要进行正确引导，以达到学生主动思考的效果。学习过程中，学生内心的障碍逐渐消除，慢慢地开始接受课堂教学，逐渐走向成熟，在提高自信心的同时也起到了深度学习的效果[2]。

三、引领学生考查题目立意，拓展学生思维

中考数学不仅考查学生对基础知识的掌握程度，更侧重于考查学生的思辨能力、逻辑推理能力。大部分中考题目包含了数学知识点和数学方法的运用考查，强调过程的推导和结果的计算。在数学教学中，教师要善于利用这一类型的题目，引导学生深挖题目立意，了解出题人的初衷、考查要点，以此来针对性地锻炼学生寻根问底、挖掘信息、探究本质、思辨推导等能力，培养学生的数学素养。

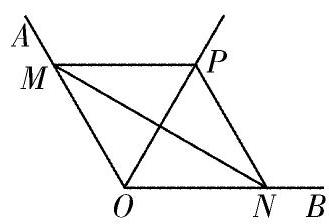
案例：如图所示，∠AOB=120°，OP平分∠AOB，且OP=2，若点M，N分别在OA，OB上，且三角形PMN为等边三角形，则满足上述条件的三角形PMN有（ ）

A.1个 B.2个 C.3个 D.3个以上

这道题属于抽象拓展结构题目，考查的知识点较多，包括角平分线的性质定理、等边三角形的判定方法、全等三角形的判定、旋转性质等，较为考验学生的抽象思维与构图能力。针对这类题目，教师在了解出题者的考查意图后，引导学生一一复习涉及的判定方法、定律性质等知识点，将概念、法则、定律、公式等抽象的内容以直观、立体、形象的方式呈现在学生眼前，加深学生对这些基础知识的印象，了解这些基础知识的应用条件和使用前提。最重要的是，在学生掌握这些基础后，教师要进行拓展延伸，帮助学生掌握这些基础知识经过变化、伪装后的各种形态，然后借由对各种形态的分析来探究数学的本质，再回到概念、法则、定律、公式等知识本身，让学生在发散思维和聚拢思维的过程中掌握数学的本质，了解以这些数学基础知识为依托来构建数学模型的方法，体会数形结合的思想，拓宽学生思维的深度和广度。

在教学中，教师通过剖析中考试题一方面能够帮助学生学习数学的基本知识和理论，提高学习的效率和巩固所学知识;另一方面也可以让学生对中考数学有更直观的了解，把握知识的整体脉络，更快地提高自己的数学成绩。

参考文献：

[1]孙媛媛，马敏.剖析中考试题 启迪深度教学[J].中学数学教学参考，2021（05）：28-30.

[2]刘念.转换研究视角 评析中考试题[J].中学物理，2021，39（04）：53-56.

（作者单位：山东省淄博市周村区第三中学，山东 淄博255300）