基于CNN-GRU SA模型的短期电力负荷预测研究
葛夫勇 雷景生
摘要:为了解决预测模型无法充分挖掘特征等问题,提出一种基于CNN-GRU SA混合模型的短期电力负荷预测方法。通过CNN模型提取输入数据的向量特征,利用双层GRU模型学习输入特征,掌握其特征规律,Self-attention机制充分挖掘输入的特征信息,最后预测出负荷值。实验采用英格兰公开数据集,实验结果表明,相较于CNN-GRU、GRU和CNN基线模型,该模型的预测精度更高,证明了该方法的有效性。
关键词:电力负荷预测;CNN;GRU;Self-attention
中图分类号:TM715 文献标识码:A 文章编号:2096-4706(2021)07-0150-05
Research on Short Term Electric Load Forecasting Based on CNN-GRU SA Model
GE Fuyong,LEI Jingsheng
(Shanghai University of Electric Power,Shanghai 200090,China)
Abstract:In order to solve the problem that the forecasting model can not fully mine features,a short term electric load forecasting method based on CNN-GRU SA hybrid model is proposed. The vector features of input data are extracted by CNN model,and the double layer GRU model is used to learn the input features and master the feature rules. The Self-attention mechanism fully mines the input feature information,and finally predicts the load value. The experiment is based on England public data set,and the results show that compared with the CNN-GRU,GRU and CNN baseline models,the prediction accuracy of this model is higher,which proves the effectiveness of this method.
Keywords:electric load forecasting;CNN;GRU;Self-attention
收稿日期:2021-03-06
0 引 言
近年来,随着智能电网、微电网等新兴电网的出现,人们对用电质量的要求不断提高。电力负荷精准预测对提升用电质量具有举足轻重的作用。如何选择一种负荷预测精准度高的模型,成为一个重要课题,因此,笔者将深度学习方法应用于负荷预测中,以提高电力负荷预测的精准度。
电力负荷预测按照预测时间长短可分为短期、中期和长期,其中短期是预测未来一个小时的电力负荷值,中期是预测未来一个月的电力负荷值,长期是预测未来一年或更长时间的电力负荷值[1]。电力负荷预测是一个时间序列问题,由单变量或多变量要素组成[2]。如果仅将历史电力负荷数据用作预测模型的输入,则称为单变量预测。在多变量预测中,其他因素也输入预测模型中。这些因素本身可以是不同的时间序列,例如天气属性(温度或湿度)、邻近区域的负载数据、电力价格,甚至是经济数据(国内生产总值(GDP))。就迄今为止所实施的大多数电力负荷预测模型而言,基本上采用多变量预测。
电力负荷预测方法大致分为三种,即传统的统计方法、基于机器学习的方法和基于深度学习的方法[3]。传统的统计方法是以时间序列为重复的固有模式,通过捕获这些模式,可以预测未来电力负荷的变化趋势。其中包括指数平滑法:最早通过采用单变量数据进行预测的方法之一。预测结果是过去观测结果的加权总和,随着观测结果的增大,加权值会以指数形式变小。自回归综合移动平均模型(ARIMA):一个比指数平滑更复杂的模型,它可以通过递归方式以预测值作为模型的输入来进行多步预测。但随着预测步骤的增多,ARIMA的效果急剧下滑。这些统计方法对数据质量具有较高的要求,对于受较多因素影响的数据表现为预测效果差、精度低。基于机器学习预测方法所涉及的开发模型,仅仅是通过用户提供的数据进行学习。与统计方法不同,输入输出映射不一定是预定义的。在训练过程中学习其方法。例如多重线性回归模型(Multiple Linear Regression,MLR)、支持矢量回归(Support Vector Regression,SVR)[4]等。机器学习模型多为浅层模型,很难更深层次地去挖掘数据特征,又存在人为干扰问题,误差较大,预测精度较差。近年来,深度学习方法在计算机视觉、自然语言处理等领域取得较好的成果,因此,这也成为负荷预测领域最新研究的方向,其中应用较多的深度学习算法有人工神经网络(Artificial Neural Networks,ANN)、卷积神经网络(Convolutional Neural Network,CNN)和循环神经网络(Recurrent Neural Network,RNN)等[5],CNN特别设计用于图像、文本分類任务中,其中网络接受二维数据。CNN用于时间序列分析,时间序列是一维数据。CNN具有权值共享和内部连接的特点,在非线性问题上有较好的性能。RNN可以解决负荷预测时序问题,具有长期依赖性。GRU(Gated Recurrent Unit)是RNN的改进模型,解决了RNN梯度爆炸和消失问 题。文献[6]为更好地挖掘数据中时序特征的联系,提高负荷预测的精度,提出一种基于卷积神经网络和门控循环单元混合神经网络的负荷预测方法,实验证明了该方法的有效性。深度学习算法中,Self-Attention机制属于Transformer的主要功能单元[7],Self-Attention机制会产生一个向量,该向量在其邻近向量上加权求和,其中权重是由数据之间关系决定的。
通过以上研究,本文提出一种基于CNN-GRU SA的短期电力负荷预测混合模型,利用CNN有效提取负荷数据的内部相邻高维特征,输入到双层GRU模型中,GRU动态提取特征规律,最后Self-Attention机制将输入的特征向量合理地进行权重分配,更好地挖掘数据之间的联系,精准预测出负荷值,实验表明,相较于其他的基线模型,该模型的负荷预测效果更好。
1 CNN-GRU SA混合模型
1.1 卷积神经网络模型
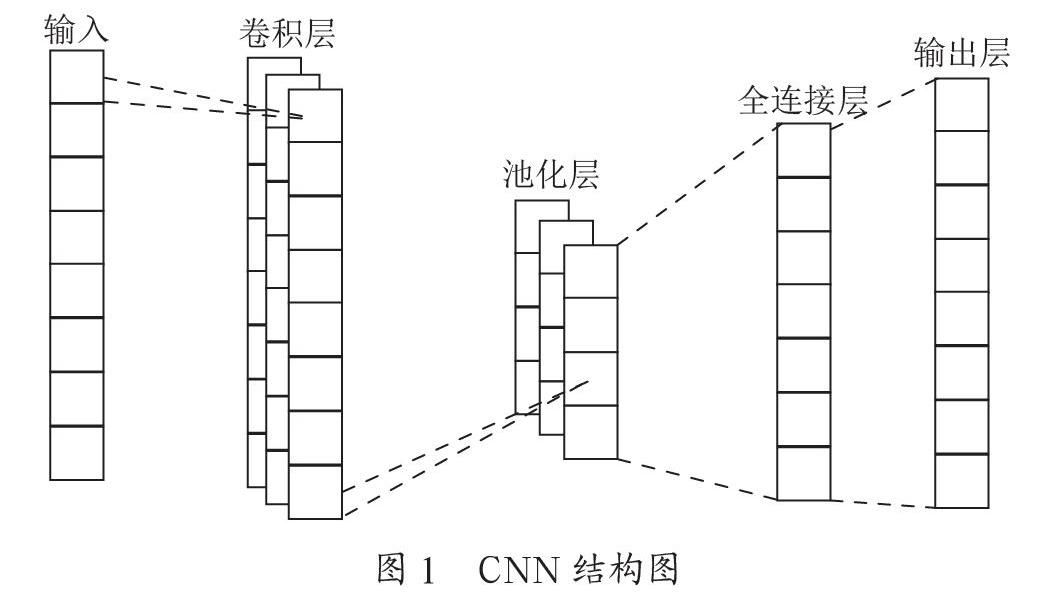
CNN是深度学习领域的典型算法模型,其优点是局部连接和共享权值,可以高效提取数据特征,其结构一般是由卷积层、池化层和完全连接层组成。其中的关键部分是卷积层,卷积层中大小各异的卷积核可以提取输入数据不同的相邻特征关系。其卷积层具有权值共享的功能,这可使权值的数量减少,降低提取输入数据特征的难度,使特征提取更加高效[8]。在卷积层之后,池化层运用扫描采样对所获取的特征图进行建模,并将其转换为隐藏层和存储单元之间更为抽象的特征。池化层在降低数据维度的情况下,减少模型参数。最后通过全连接层将之前所有特征向量连接起来,一般采用ReLU函数来激活全连接层。其结构如图1所示。
1.2 GRU模型
RNN易产生梯度爆炸和消失的问题。梯度爆炸是循环神经网络所存在的一个问题,其中“长期”时序分量梯度的增長是“短期”时序分量梯度增长的几倍。GRU和LSTM(Long Short Term Memory Network)是改进后的循环神经网络(RNN)类型。与CNN不同,RNN具有向后连接的特点,以反馈方式极大地影响模型的精度,这些问题皆可由LSTM模型予以解决。在RNN的高级体系结构中,是为了解决时序特征中长期依赖问题而采用的。LSTM的内部由单元块构成。单元状态和隐藏状态从一个单元块传输到另一个单元块,而内存块用于表达记忆门状态。LSTM架构包括三个门:输入门、遗忘门和输出门[9],而GRU只有两个门:重置门和更新门。更新门用于检查较早的单元内存以保持当前时间步的活动状态,重置门用于将下一个单元格的输入序列与前面单元格的内存组合在一起。然而,LSTM在某些方面有所不同,首先,GRU单元由两个门组成,用以替代LSTM的三个门[10]。其次,将LSTM中的输入门和遗忘门合并为更新门,并直接应用于隐藏状态的复位门中。GRU结构如图2所示。其中,×为矩阵乘积,σ为激活函数sigmod,?为激活函数tanh。
图中输入是xt,上一时刻状态变量为ht-1,实时状态变量为ht, 为实时候选集状态。GRU单元的数学表达方程为:
rt=σ[Wr·(ht-1,xt)] (1)
Zt=σ[Wz·(ht-1,xt)] (2)
=?[·(rt·ht-1,xt)] (3)
ht=(I-zt)·ht-1+zt· (4)
其中,单位矩阵是I,Wr、Wz、 为GRU的各个权重参数。
1.3 Self-Attention模型
在传统编码器-解码器网络中,当输入序列很长时,很难获得全部重要信息。注意机制打破了传统编码器-解码器结构的限制,使解码器仅依赖于具有固定长度的矢量。注意机制是用以获取相关信息的一种有效方法。一方面,它允许解码器在解码过程中的每一步查询最相关的信息;另一方面,它大大缩短了信息流的距离。解码器可以通过一步操作获得任何时刻所需的所有信息。这些优点的存在,使得注意机制已广泛应用于各种模型。Vaswani等人提出了Transformer模型[7],它摒弃了使用循环神经网络或卷积神经网络作为编码器和解码器的传统方法,完全利用注意机制在不同的网络层之间传输信息,称为自我注意机制,在自然语言领域取得了良好的效果。
自我注意机制是用以计算相关性的一种方法。其结构图如图3所示。可以理解为将名为Query的矩阵作为查询对象,将名为Key的矩阵作为匹配对象,将名为Value的矩阵作为目标。
查询(Q)、键(K)和权值(V)可以从式(5)、式(6)和式(7)中获得,它们是训练过程中的重要权值矩阵。首先,计算输入向量的查询与其他输入向量(包括其本身)键值之间的相似度,将其作为权重。然后取一个加权平均值(包括其本身),得到自我注意输出向量。总之,将输入序列的每个向量与其他向量进行加权平均,融合所有的输入信息生成新的向量,增强原始序列信息的表达。因此,自我注意力的输出序列是输入本身,但通过计算每个输入向量与其他输入向量之间的关系,可以增强原始信息的表达。此外,自我注意机制为了保持输入信息空间特征向量之间的联系,通过每个自我注意机制以线性组合的方式获得最终输出。
Q=X·WQ (5)
K=X·WK (6)
V=X·WV (7)
自我注意机制中各个输入序列之间的关联度是通过以下步骤实现的。首先,通过点乘计算查询与键的相似度,通过softmax函数获得权值。然后,将权重加权到该值,得到自我注意的输出向量。与注意机制略有不同,自我注意机制在计算时有一个附加的比例因子,当内部产品过大时可以避免重叠。通常,键的维度作为值。自我注意机制中计算方法可通过式(8)来表示[11]:
Attention(Q,K,V)=soft max()·V (8)
1.4 CNN-GRU SA混合模型
基于CNN-GRU SA混合模型的负荷预测框架如图4所示,其包含输入层、CNN、GRU、Self-attention和输出层。将之前的多变量一维数据输入到CNN中。本文所用的CNN模型是選择一个卷积层和一个池化层为一组,选取两组进行特征提取,这样可以充分提取历史时间序列中的特征,并通过池化层得到最大特征向量。进行两组卷积和池化操作提取的特征更彻底,将提取出的最大特征向量输入到连接层进行权值分配,以获取更优的数据特征。GRU对CNN输出的特征进行迭代学习,更好地学习特征内部规律,获取特征之间的长期依赖关系,并能减少训练时间,由于负荷数据为时间序列,其数据序列距离过长,GRU模型在学习训练过程中也会造成部分信息丢失,不能全面学习整个时间序列数据,以致降低预测精准度。Self-attention模型输出序列是输入本身,通过计算每个输入向量与其他输入向量之间的关系,分配不同的权重因子,由于不是按照时间序列去计算,因此可以通过不同位置信息进行学习。在长距离依赖上,由于Self-attention是每个数据都要计算attention,不管他们之间的距离有多长,最大的路径长度也都只有1,因此可以捕获长距离依赖关系。因此,基于CNN-GRU SA电力负荷预测模型,通过多个模型的融合,对历史数据进行全面深入的挖掘,以获得更好的负荷预测效果。
2 实验与结果分析
2.1 实验数据集与预处理
实验数据来自ISO-NE上进行了区域/系统级负载预测案例研究的负荷数据集。ISO-NE是一个独立的区域输电组织(RTO),服务于新英格兰六个州,本实验选用新英格兰某一个州2014年1月1日至2015年12月31日2年内的负荷数据,一天采集24个负荷点。其中抽取历史数据中的日期、温度以及负荷值作为实验数据,按8:2的比例将其划分为训练集和测试集。
数据集中缺失的数据用之前相同日期的数据来代替,数据异常问题可通过水平和垂直处理法进行修正,从而使预测结果更加精准。由于数据集中的数据单位不同,无法进行同一量纲处理,因此对数据进行归一化处理:
xn= (9)
其中,x为历史负荷数据,xmax为历史负荷数据最大值,xmin为历史负荷数据最小值。将数据值归一到[0,1]中。
2.2 实验评价标准
本实验采用平均绝对误差(Mean Absolute Error,MAE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方根误差(Root Mean Square Error,RMSE)为实验结果评价指标,计算公式为:
MAE= (10)
MAPE= (11)
RMSE= (12)
其中,为预测值,yi为真实值,MAE利用预测值和真实值的绝对平均值去判断,MAE、MAPE是判断模型预测的好坏,RMSE是判断模型预测的精度,这些判断指标值越小越好。
2.3 实验环境
本实验环境配置如表1所示。
2.4 模型介绍和预测结果分析
本文所选的基线模型为CNN、GRU和CNN-GRU混合模型,其中,CNN选择两层卷积层和池化层,卷积深度为32和64,卷积核的尺寸为2×2×2×32与2×2×2×64,卷积步长为1,激活函数为ReLU。GRU的神经单位数量为64、32。
表2是选取测试集中三个月的预测误差结果,不同月份的预测精度因受本月气候、节假日等因素的影响也会有所不同,由表2可知CNN-GRU SA模型MAE最低为75.33、最高为76.31;MAPE最低为0.026 3,最高为0.031 2;RMSE最低为94.11,最高为97.78。CNN-GRU SA模型MAE、MAPE、RMSE误差指标较其他模型更低,预测更加准确。其中Self-attention机制具有更长期依赖和不按顺序进行权重因子分配的特点,对提升CNN-GRU SA模型的精度起到关键作用。
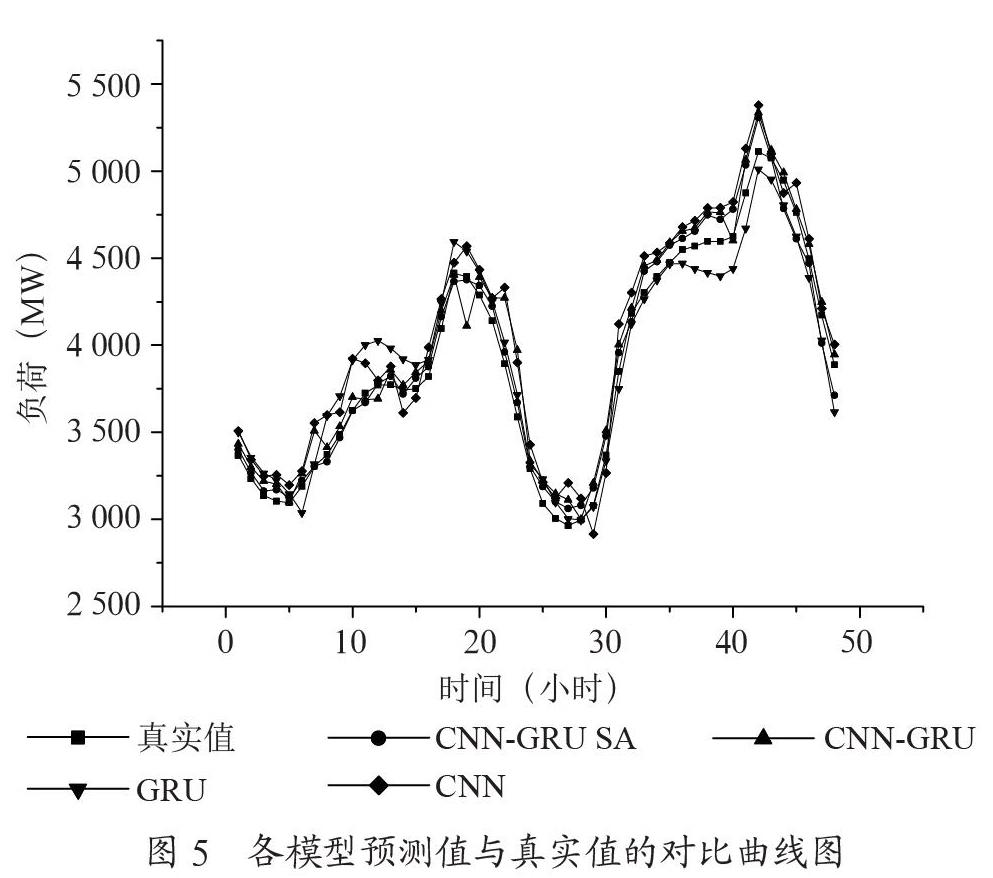
为了更加直观地了解各模型短期预测值与真实值之间的差别情况,选取新英格兰某州2015年10月中某两天的数据为研究对象,以小时为单位,对48个预测点进行对比,如图5所示,一天中1:00~6:00为负荷低谷期,16:00~22:00为负荷高峰期,这两个阶段,负荷变化幅度较大,各模型在此时的预測精度相较于其他时间段的精度要低一些,其中CNN-GRU SA模型在这两个时刻的预测值更接近真实值,比其他模型更精准,其中CNN模型的预测精度最差。其他时刻CNN-GRU SA模型的预测值也更靠近真实值,通过观察48小时负荷预测曲线,可以看出本文提出的CNN-GRU SA模型的预测值相较于其他模型的预测值,整体上更加平稳,更靠近真实值。
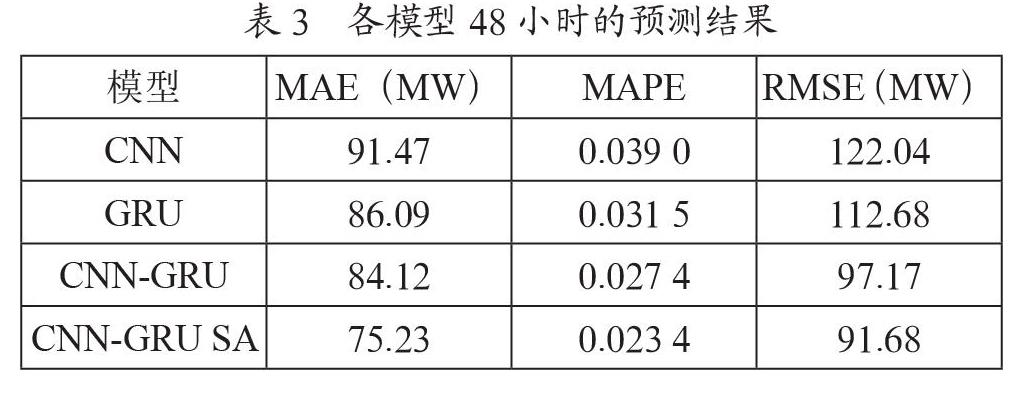
表3是由图5计算出来的预测结果,由表3可知,CNN-GRU SA模型MAE值为75.23、MAPE值为0.023 4、RMSE值为91.68,较CNN-CRU基线模型分别降低了8.89、0.004和5.49;较GRU基线模型分别降低了10.86、0.008 1和21;较CNN基线模型分别降低了16.24、0.015 6和30.36,可以看出在48小时实验数据负荷预测中,CNN-GRU SA模型各个预测误差指标都比其他模型小,预测精度更高。
3 结 论
本文提出一种基于CNN-GRU SA混合模型的负荷短期预测方法,采用英格兰某州公开的数据集,其中包含负荷、日期和气候数据,先通过改进后的CNN模型进行特征提取,双层GRU对输入特征做进一步的特征提取,最后通过Self-attention机制对GRU输出的特征按不同权重进行配置,并根据顺序序列进行计算,充分提取出不同位置的重要信息,获得更长期依赖的特征,最后预测出更接近真实数据的负荷值。实验结果表明,本文提出的CNN-GRU SA模型较其他基线模型的预测误差更小,预测精度更好。接下来的工作是研究Self-attention机制,改进或结合其他模型,对公开数据集进行测试,以开发出预测效果更好的负荷预测模型。
参考文献:
[1] 洪发.基于深度学习的短期电力负荷预测方法 [D].广州:广东工业大学,2020.
[2] 王文卿.基于卷积神经网络的电力系统短期负荷预测研究 [D].青岛:青岛大学,2020.
[3] 康重庆,夏清,张伯明.电力系统负荷预测研究综述与发展方向的探讨 [J].电力系统自动化,2004(17):1-11.
[4] 翟永杰,王静娴,周黎辉.基于模糊支持向量机的电力系统中期负荷预测 [J].华北电力大学学报(自然科学版),2008(2):70-73.
[5] 姚栋方,吴瀛,罗磊,等.基于深度学习的短期电力负荷预测 [J].国外电子测量技术,2020,39(1):44-48.
[6] 姚程文,杨苹,刘泽健.基于CNN-GRU混合神经网络的负荷预测方法 [J].电网技术,2020,44(9):3416-3424.
[7] VASWANI A,NOAM S,PARMAR N,et al. Attention is all you need [C]//NIPS17:Proceedings of the 31st International Conference on Neural Information Processing Systems.Red Hook:Curran Associates,2017:6000-6010.
[8] 陆继翔,张琪培,杨志宏,等.基于CNN-LSTM混合神经网络模型的短期负荷预测方法 [J].电力系统自动化,2019,43(8):131-137.
[9] 王永志,刘博,李钰.一种基于LSTM神经网络的电力负荷预测方法 [J].实验室研究与探索,2020,39(5):41-45.
[10] 邓带雨,李坚,张真源,等.基于EEMD-GRU-MLR的短期电力负荷预测 [J].电网技术,2020,44(2):593-602.
[11] 闫雄,段跃兴,张泽华.采用自注意力机制和CNN融合的实体关系抽取 [J].计算机工程与科学,2020,42(11):2059-2066.
作者简介:葛夫勇(1994—),男,汉族,江苏徐州人,硕士研究生在读,研究方向:电力大数据;雷景生(1966—),男,汉族,陕西韩城人,教授,博士,研究方向:人工智能、电力大数据。

