基于阻隔介质的勘探震源药柱殉爆距离推算
陈凯滨, 李 彪, 刘 伟, 胡 峰, 李子轩, 吴晓华
(1.中国石油东方地球物理勘探公司 西南物探分公司,成都 610213;2.中国石油西南油气田川中采气管理处,遂宁 629000)
0 引言
地震勘探哑炮处置的方法主要有三种:①井下重新装药诱爆[1];②取出井下拒爆药包[1];③借鉴深孔爆破打平行(径向)井的殉爆处置。前二种方法常因激发井中的填塞物无法取出而难于实施。殉爆法虽可以规避取井中填塞物这一瓶颈,但该技术应用的关键点没有给出在不同阻隔介质下的井下药柱最大殉爆距离。李铮等[2]研究获得了空气介质条件下各种工业炸药的殉爆距离参考成果;宗琦[3]就岩石中爆炸冲击波能量分布规律也进行了探索;张福宏[4]就炸药药卷在炮眼中殉爆距离计算经验式的建立;王晨等[5]就壳装炸药殉爆实验和数值模拟;冯海龙[6]就爆炸冲击波的简化计算方法概述,但均未形成殉爆距离随不同阻隔介质变化的规律性认识和经验算法。为此,笔者首先通过井筒内空气介质轴向殉爆实验,获取药柱殉爆基值,根据爆轰冲击力传播作用原理和爆炸相似原理和喻长智等[7]柱状药包爆破冲击波作用区域的理论计算,建立起勘探炮井内乳化震源药柱殉爆距离推算的经验公式。而后按不同间距钻相等井深的平行井、主发井装药深度及装药量与被发井一致,监测验证砂岩阻隔介质下井间径向殉爆结果与计算结果的符合度。
1 爆轰殉爆原理
殉爆是指当炸药(主发药包)发生爆炸时,由于爆轰波的作用引起相隔一定距离的另一药包(被发药包)爆炸的现象和李仕洪等[8]工业炸药殉爆距离试验方法的改进。无论处于介质中任何一点,只要某点的起爆能量达到炸药的最小起爆感度,位于该点的炸药既能被引爆。勘探深孔殉爆可分为沿井筒的轴向殉爆和井筒间的径向殉爆二种方式,当药包间为岩石介质时,由于岩石直接受到主发药包爆炸的巨大压力和高温作用,岩石受到压缩而形成空腔破碎带(半径不超过药包半径的2倍~7倍)和裂隙带(井孔半径8倍~150倍)[7],爆轰冲击波穿过破碎带后,其冲击压力仍能达到邻近被发药包起爆的临界压力,则被发药包出现殉爆。
2 实验设计
距井筒线30 m,铺设24道地震勘探记录仪、逐点布置L20-S爆破测振仪实施殉爆监测,进行井内轴向饱和砂介质的殉爆测试实验,获取轴向炮井乳化震源药柱殉爆基值。
2.1 轴向殉爆激发及监测方法
1)井筒及记录仪器布设(图1)。24道小折射仪排列长度按高速层折射波时距曲线的控制距离不小于40 m为原则设计[9],实时采集各试验炮井激发时的爆破能量;使用L20-S爆破测振仪,确保振动传感器与介质紧密接触,不得出现松动与滑动现象[10],现场分别监测各试验炮井激发时的爆破振动峰值。

图1 轴向殉爆激发及监测方法示意图
2)测定固定药量爆破能量。地表砂岩区钻2口炮井,井深为15 m,分别装1 kg、3 kg震源药包,获取爆破能量值和爆破振动峰值,该值用于3 kg药量分析为1 kg主发、2 kg被发在不同间距饱和砂介质下轴向殉爆测试记录的能量及振动峰值速度比较。
3)殉爆装药。采用成型药柱空筒,按设计殉爆间距值制作模具,保证主发药柱与被发药柱间隔为0 cm、5 cm、10 cm、20 cm、30 cm、40 cm共6种间隔距。
2.2 实验结果
2.2.1 爆破振动峰值监测数据
比较表1中测振仪峰值速度,分析激发殉爆间隔距离在0 cm~30 cm范围,其振动峰值速度高于1 kg爆破振动峰值,近似于3 kg的爆破振动峰值速度,可判定为被殉爆;间隔40 cm殉爆的爆破振动峰值近似1 kg爆破振动峰值,可判定未被完全殉爆。
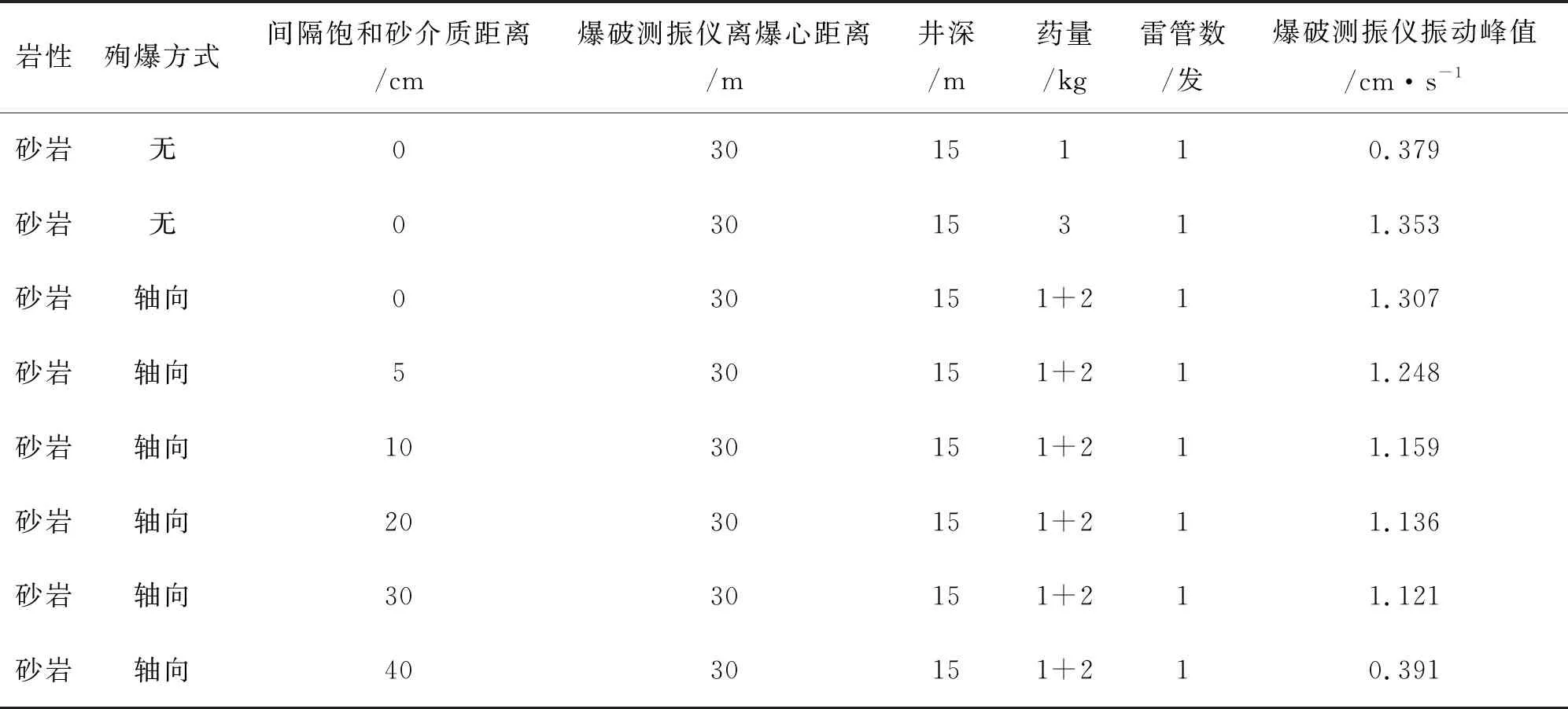
表1 侏罗系轴向炮井殉爆爆破振动数据表
2.2.2 小折射仪采集记录数据
从24道折射仪监视记录定性和道能量的定量比较看出(图2、图3):分析激发殉爆间隔在0 cm~30 cm范围,其能量与3 kg的爆破能量接近,可判定为被殉爆;间隔40 cm殉爆的爆破能量近似1 kg爆破能量,可判定未被殉爆。其中显示的能量误差主要因为非绝对同一时刻激发实验,各道记录的环境噪声变化所致。
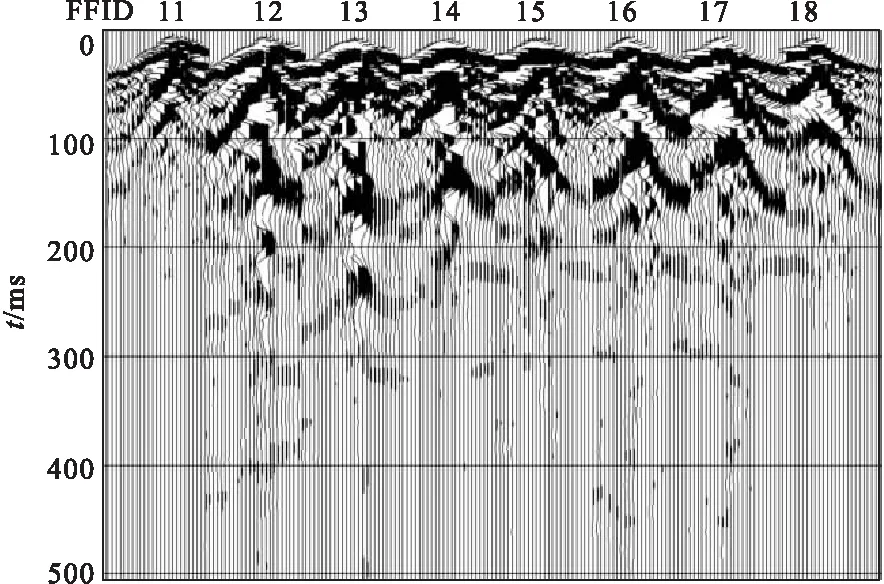
图2 间距0 cm、0 cm、0 cm、5 cm、10 cm、20 cm、30 cm、40 cm轴向炮井殉爆监视记录
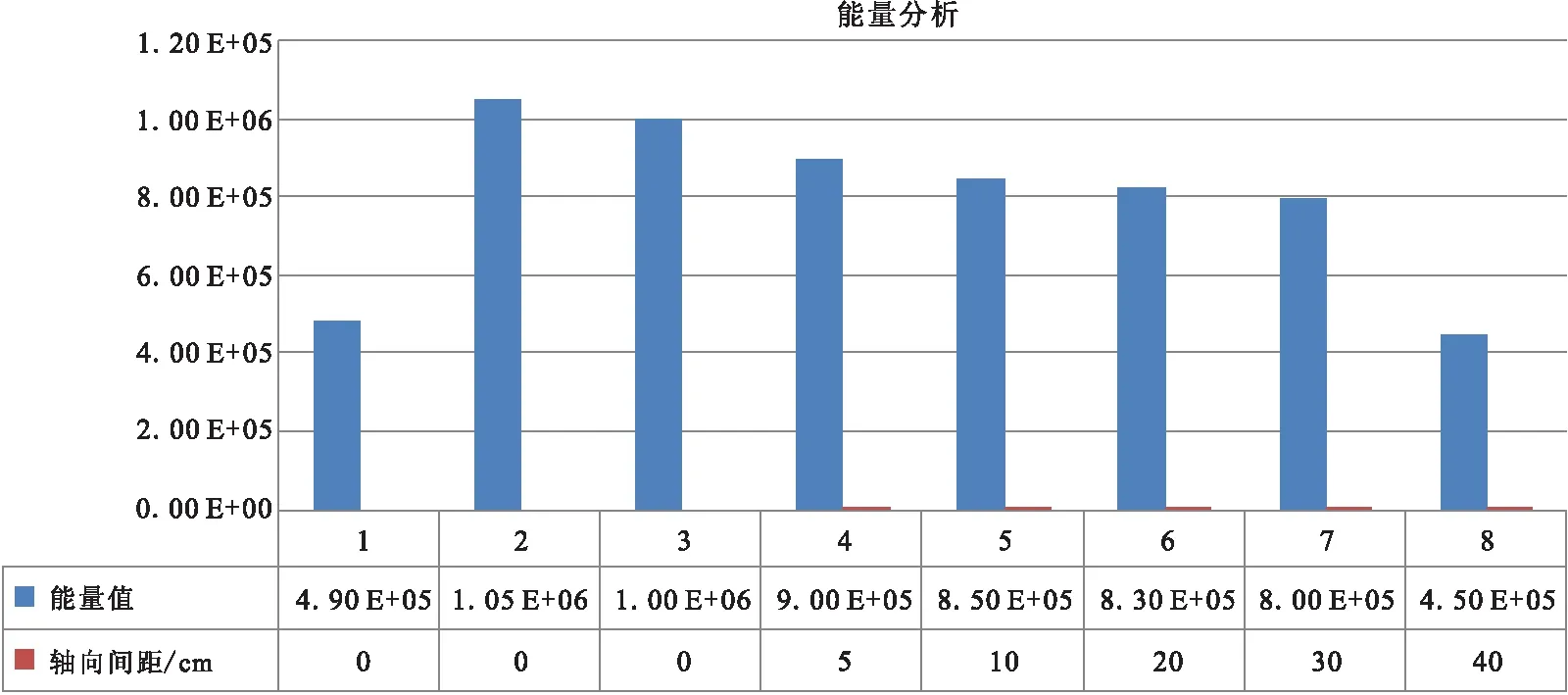
图3 间距0 cm、0 cm、0 cm、5 cm、10 cm、20 cm、30 cm、40 cm轴向炮井诱爆单炮能量
2.2.3 实验结论
通过饱和砂介质下轴向殉爆试验,测振仪和小折射仪记录的数据说明:主发药1 kg,被发药2 kg,井筒内最大殉爆距离≤30 cm。
3 计算经验公式的建立
饱和砂介质条件下的井筒内轴向殉爆实验,条形药柱主发药与被发药药柱半径一致,爆轰传播为轴向,鉴于乳化药柱起爆的药型特点,在不考虑主发与被发药包方向的前提条件下,推导如下:
根据冲击波传播作用数学表达式[7],即
p=p0/Rα
(1)
式中:p为岩石中冲击波峰值压力;p0为炸药爆炸后岩石界面上的初始冲击波压力;R为比距离,R=r/re;r为与冲击波压力p对应点处距爆源的距离;re为药包半径;α为压力衰减系数。则
轴向殉爆冲击波:
p轴=P0/Rα砂
(2)
径向殉爆冲击波:
p径=P0/Rα介
(3)
在井深、震源药柱、装药结构一致的情况下,利用爆破相似原理,不考虑主发与被发药包方向的前提条件下,轴向和径向殉爆的冲击波一致。依据土中爆破机理和轴向炮井殉爆试验数据,轴向间隔介质r砂为30 cm,药柱半径re为3 cm;r介为径向介质间距,α砂为饱和砂介质应力波衰减系数,α介为阻隔介质衰减系数,则
p0/(r砂/re)α砂=p0/(r介/re)α介
(4)
即 (r砂/re)α砂=(r介/re)α介
r介/re=[(r砂/re)r砂]1/α介
依据轴向炮井空气介质殉爆获取的基值(r砂取30 cm,re取3 cm,α砂为饱和砂介质应力波衰减系数取1.05[7]),可推算出以下比例距离计算经验公式:
r介=3[(r砂/re)1/1.05]1/α介
根据比例距离公式[6]:r介=R/Q1/3
R=3[(r砂/re)1/1.05]1/α介Q1/3
(5)
其中:r砂取30 cm;re取3 cm;α介为岩石应力波衰减系数;R为殉爆距离,cm;Q为主发药量,kg。
则式(5)可简化为:
R=3[(10)1/1.05]1/α介Q1/3
(6)
石灰岩、砂岩、泥岩泊松比μ见表2。

表2 岩石泊松比μ

表3 石灰岩、砂岩、泥岩α介值
结合本次侏罗系砂岩地层井中(轴向)间隔为30 cm可殉爆试验数据,r取30 cm。分别代入式(6)得1 kg~6 kg石灰岩、砂岩、泥岩介质殉爆距离模拟计算经验值(表4、图4)。
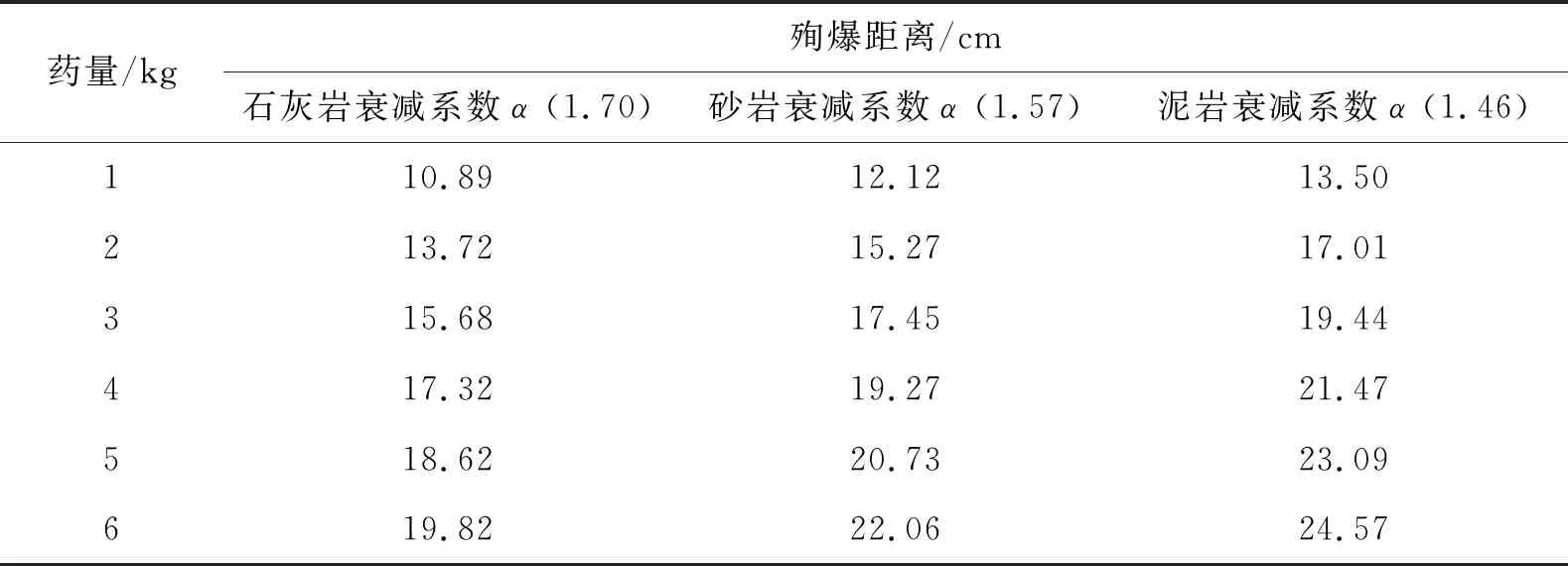
表4 石灰岩、砂岩、泥岩介质殉爆距离模拟计算经验值

表5 测试及验证试验径向炮井殉爆振动峰值监测结果
根据宗琦[3]岩石中爆炸冲击波能量分布规律初探,α介=2-μ/(1-μ)石灰岩泊松比μ取0.23,砂岩泊松比μ取0.30,泥岩泊松比μ取0.35,则石灰岩、砂岩、泥岩α介值(见表3)。

图4 石灰岩、砂岩和泥岩石介质殉爆距离模拟计算经验值曲线图

图5 径向殉爆激发与监测方法示意图

图6 砂岩间距30 cm、50 cm、70 cm、90 cm径向殉爆监视记录
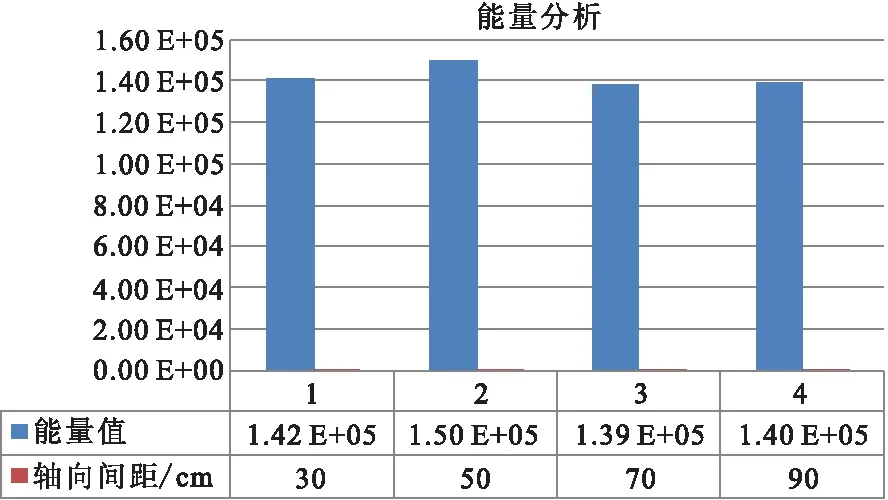
图7 砂岩间距30 cm、50 cm、70 cm、90 cm径向殉爆单炮能量
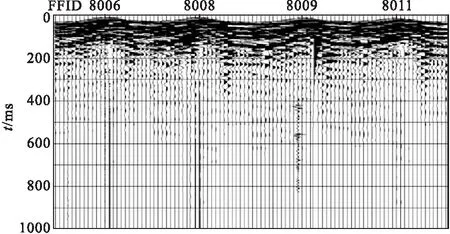
图8 砂岩间距40 cm、60 cm、80 cm、100 cm径向殉爆监视记录
4 验证测试
距井筒线30 m,铺设24道地震勘探记录仪、逐点布置L20-S爆破测振仪实施殉爆监测,进行径向井(井深为15 m,药量为6 kg)阻隔介质不同间距(30 cm、40 cm、50 cm、60 cm、70 cm、80 cm、90 cm、100 cm)的殉爆验证测试实验(图5)。
4.1 测振仪振动峰值监测数据
从图5可以看出砂岩和灰岩地层各间距殉爆爆破振动峰值接近,无明显突出峰值,说明主发药起爆后,设计间隔30 cm~100 cm的被发药未殉爆。
4.2 24道小折射仪采集资料数据
通过24道小折射仪记录的单炮爆破能量,主发炮孔药包爆炸时,爆破能量未见明显增大,与爆破振动监测结果一致(图6~图11)。

图11 灰岩间距30 cm、50 cm、70 cm、90 cm径向炮井殉爆单炮能量
4.3 验证结果
通过径向殉爆试验,根据爆破测振仪和24道小折射仪采集的数据,主发炮井在间距30 cm~100 cm,药柱间介质为砂岩和灰岩条件下,被发炮井内药包未被殉爆。
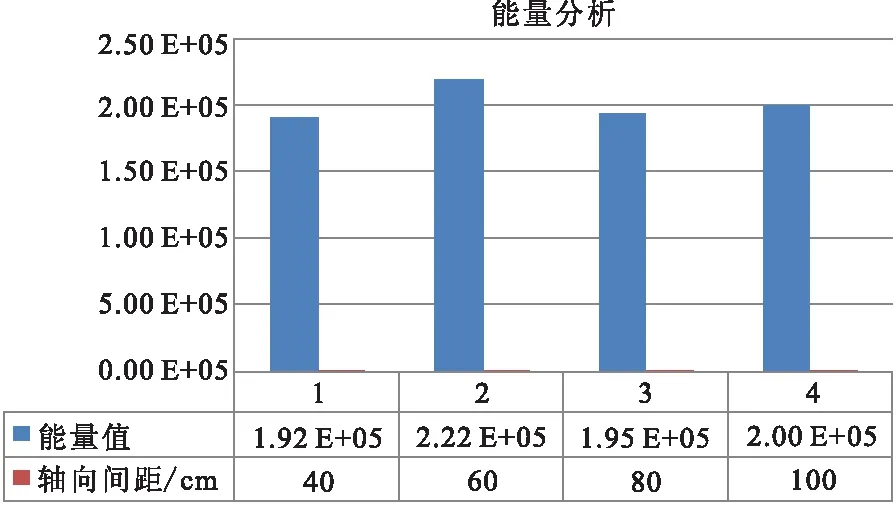
图9 砂岩间距40 cm、60 cm、80 cm、100 cm径向殉爆单炮能量
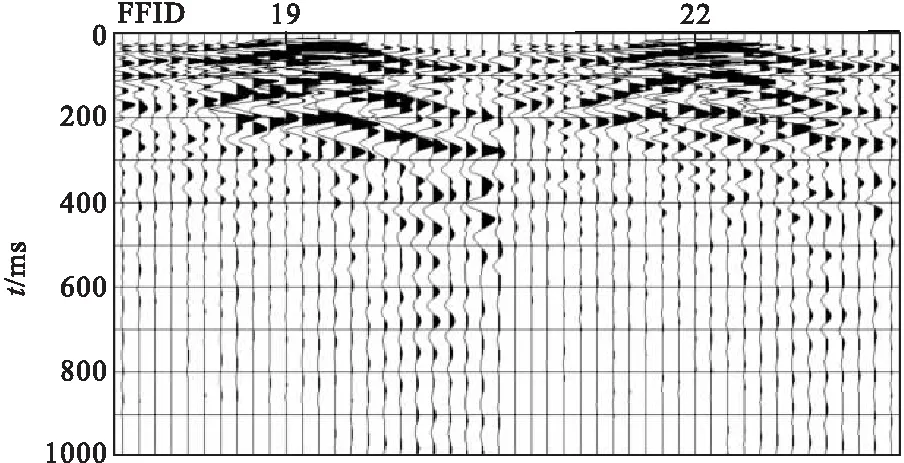
图10 径向主发炮井、被发炮井激发监视记录
5 结论
通过本次殉爆法哑炮处置测试研究,得到以下结论:
1)开展轴向殉爆试验,得到主发乳化炸药为1 kg,泥砂介质下殉爆可靠性边界距离为30 cm~40 cm;径向殉爆试验,主发乳化炸药为4 kg、6 kg,泥砂介质下径向(平行井)殉爆边界距离小于30 cm。
2)基于测试和验证数据趋势分析,利用爆破相似原理,建立起阻隔介质下的勘探震源药柱炮井间径向殉爆距离计算的经验公式,形成的经验数据用于砂岩介质区殉爆验证测试,所得结果吻合度高。
3)形成了地震勘探哑炮轴向殉爆处置技术,在取出井中填塞物条件下,可以推广轴向殉爆处置技术的应用。
4)借鉴试验和探索演算结果,地震勘探深孔爆破出现哑炮,采用径向(平行井)殉爆处置法,由于殉爆距离小,对钻平行孔实施工艺要求高,难度大,不建议采用径向(平行井)殉爆方式处置哑炮。

