亥姆霍兹线圈磁场的均匀范围研究和可视化
周群益,莫云飞,周丽丽,侯兆阳
(1.广州理工学院通识教育学院,广东 广州 510540;2.长沙学院电子信息与电气工程学院,湖南 长沙 410022;3.赣南医学院医学信息工程学院,江西 赣州 341000;4.长安大学理学院,陕西 西安 710064)
亥姆霍兹线圈是由两个半径相同、电流大小和方向相同的共轴圆环组成,不少文献研究了亥姆霍兹线圈均匀磁场区域的问题。环电流磁场的计算涉及两类完全椭圆积分,早期的学者通过椭圆积分表手工计算两类椭圆积分,效率低、精度差[1-4]。后来有学者利用电子计算机计算,效率和精度有所提高,还能画出曲线图[5-6]。近年来,有学者利用Mathematica计算两类完全椭圆积分,并绘制曲线和曲面,效率和精度大大提高[7-11]。也有一些学者利用MATLAB计算两类完全椭圆积分,并绘制曲线和曲面,效果也不错[12-14]。有的学者设计了Mathematica和MATLAB的程序,绘制了均匀区域图[15-18]。不过,这些学者没有将公式无量纲化,画出的图形不够规范。莫云飞等用MATLAB精确地绘制了亥姆霍兹线圈的均匀区域,但是还不够系统和全面[19]。文章画出了亥姆霍兹线圈在临界条件下磁感应强度分量和合磁场以及方向曲面,增加磁感应线说明了两环之间的距离对均匀区域大小和形状的影响。文后附有两个主程序和函数文件,其中主程序用参数调用函数文件,第一个函数文件说明了磁感应强度分量与合磁场以及方向曲面的画法,第二个函数文件说明了磁感应线和均匀区域的画法。这两个函数文件使用了一定的编程技巧,有一定的参考价值。
1 亥姆霍兹线圈的磁场
如图1所示,取x轴为纵轴,z轴为横轴,两环共z轴。设两个圆环的半径为a,通有同方向的电流I,两环之间的距离为2L。
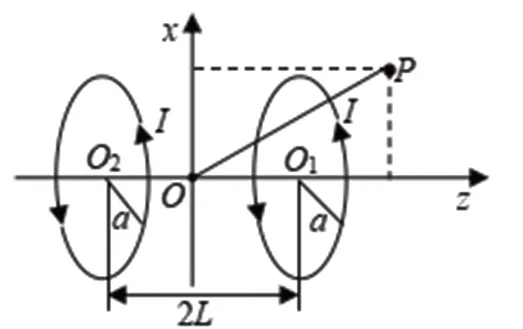
图1 亥姆霍兹线圈
如果将左环或右环移到原点,环电流产生的磁感应强度的两个分量分别为[20-22]:
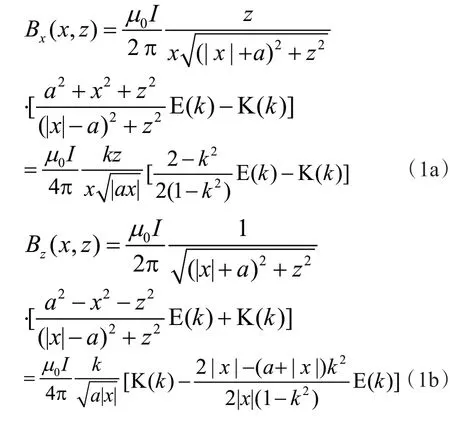
其中k称为模数,其平方为:
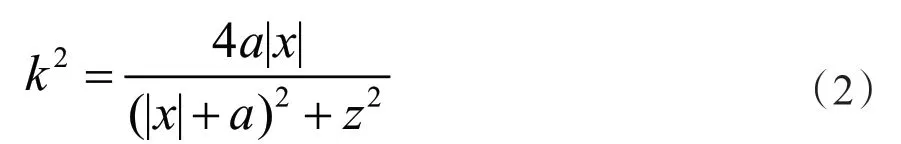
K(k)、E(k)分别为第一类完全椭圆积分和第二类完全椭圆积分:
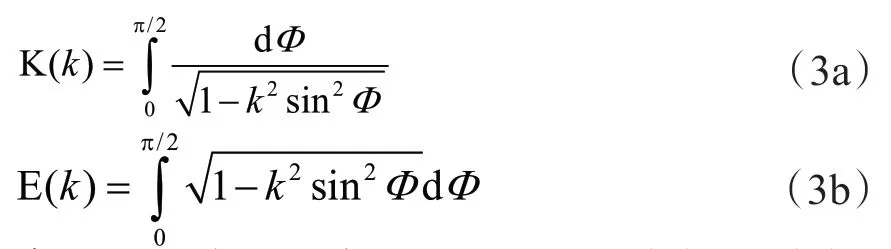
当x= 0时,必 有k= 0。而K(0)= E(0)= π/2。对式(1a)的第一个等式求x→0时的极限,可得:

对式(1b)的第一个等式求x→0时极限,可得:
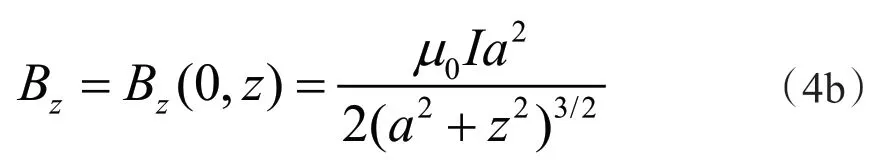
这是轴线上的磁感应强度,与电磁学教材中的公式相同。当z= 0时,可得:
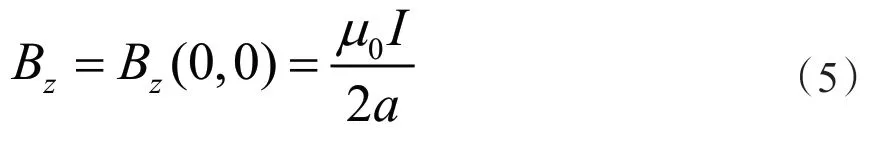
这是环心处的磁感应强度,用B0表示。
将式(1a)(1b)中的z换为z-L,即可得右环O1产生的磁场的两个分量B1x(x,z)和B1z(x,z);将式(1a)(1b)中的z换为z+L,即可得左环O2产生的磁场的两个分量B2x(x,z)和B2z(x,z)。两个线圈产生的合磁场的两个分量在左右两环产生的分量之和分别为Bx(x,z)和Bz(x,z),由此可以计算合磁场的大小和方向。
当z= 0时,可得原点的磁感应强度:
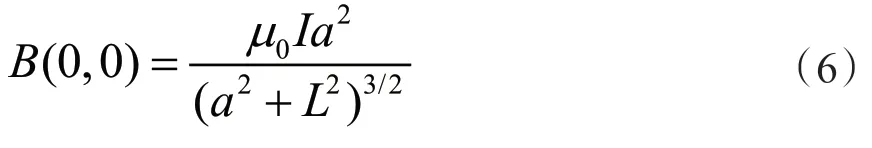
这是一个鞍点,其磁感应强度用BS表示。
在z= 0处,令,可得a2= 4L2,所以2L=a,这是临界距离。z= 0处的临界磁场为:
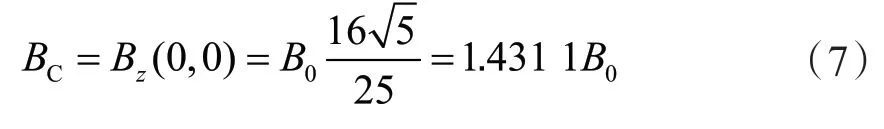
2 磁感应强度的可视化
取半径a为长度单位,则无量纲的坐标和长度为:
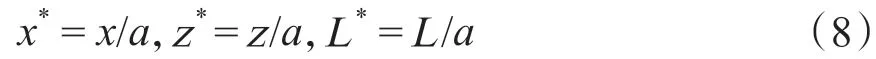
取B0=μ0I/2a为磁感应强度单位,即可将磁感应强度的公式无量纲化。注意,L*是可调节的参数,当L*= 1/2时,它就是临界无量纲距离。
根据磁感应强度的无量纲公式,利用ellipke函数可以计算椭圆积分,利用surf指令可以绘制曲面(见附录1)[23]49-52。
(1)亥姆霍兹线圈的临界磁感应强度的z分量Bz的曲面如图2所示,点(±a,±L)是奇点,表示环所在的位置,奇点处出现4个“背靠背的峰”和4个“面对面的谷”。
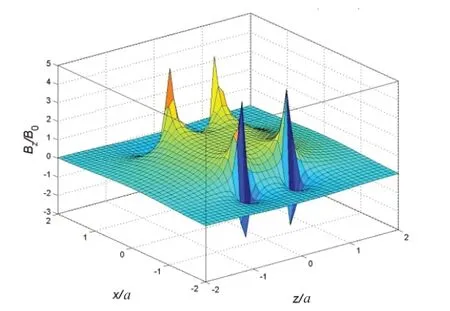
图2 临界磁感应强度z分量的分布面
(2)磁感应强度的x分量Bx的曲面如图3所示,奇点处出现4个“面朝背的峰”和4个“面朝背的谷”。
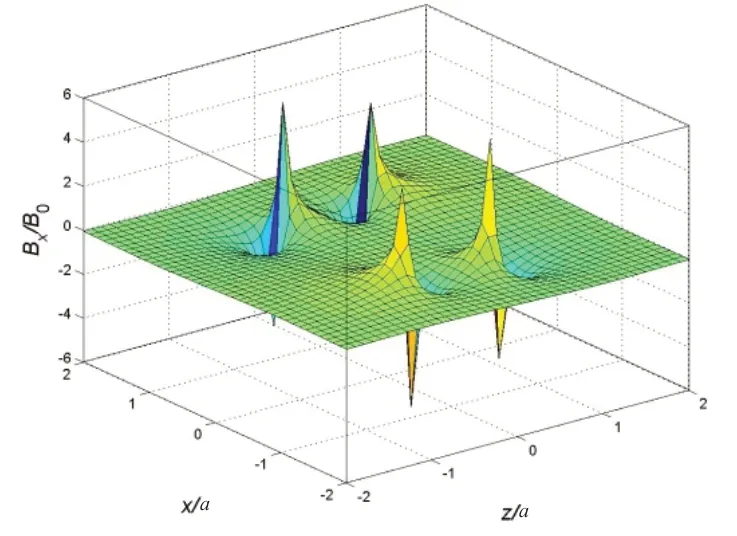
图3 临界磁感应强度x分量的分布面
(3)合磁场B的曲面如图4所示,中心处比较平坦,说明此处接近于匀强磁场,圆环处是4个很高的峰,外面磁场比较弱。
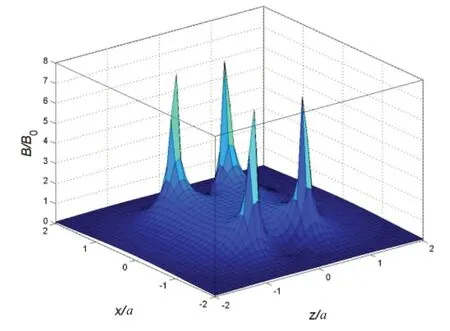
图4 临界合磁场的分布面
(4)合磁场B的方向角α的曲面如图5所示,在x= 0的z轴上,α= 0;在两环之间,α随着极角θ的增加变化较小,说明磁场比较均匀;在两环之外,α随着θ的增加而增加;当θ取某些值的时候,α发生从π到-π的跃变。
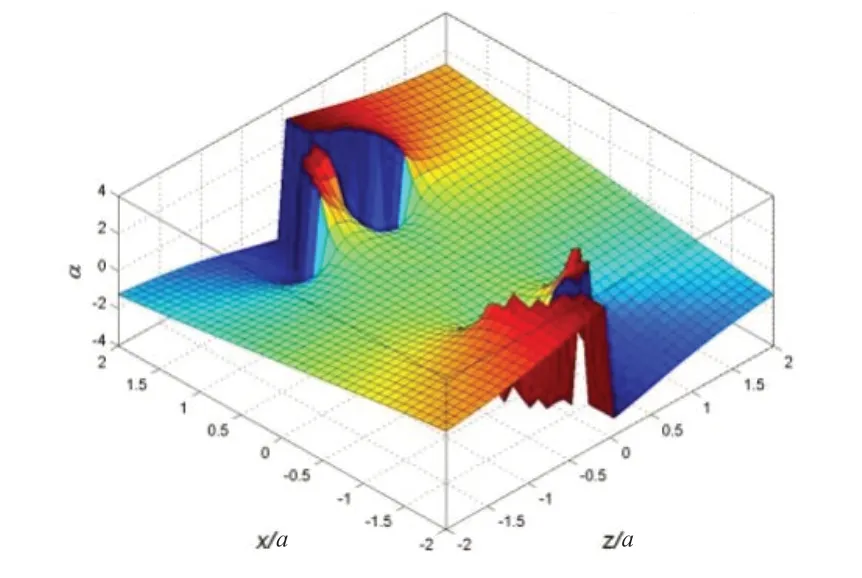
图5 临界合磁场方向的分布面
3 磁场均匀区域的可视化
利用三维等高线指令contour3可画等值线,利用流线指令streamline可以绘制磁感应线(见附录2)[23]。
取|B–BS| ≤ 0.01BS为线圈的均匀范围,即0.99BS≤B≤ 1.01BS。
(1)当L=LC= 0.5a时,亥姆霍兹线圈临界截面和磁场的均匀区域以及磁感应线如图6所示。两个电流从下面流入,从上面流出。磁感应线在原点附近是平行的,因而是匀强磁场。磁场BS=BC= 1.431 1B0的等值线恰好经过原点并包围4个电流;B= 1.01BC的4条等值线分别包围了4个电流,4条曲线并不连接;B= 0.99BC的等值线是一条曲线,同时包围了4个电流,曲线如同“X”形状。B= 1.01BC的等值线与B= 0.99BC的等值线之间的区域就是线圈临界磁场的均匀范围。均匀区域呈现“八爪”形状,一对“爪”包围一个电流。
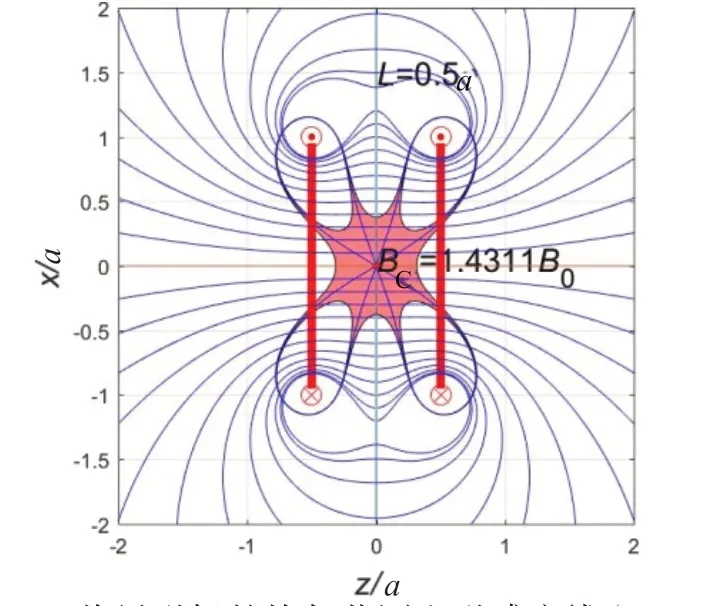
图6 临界磁场的均匀范围和磁感应线(L=0.5a)
(2)当L=0.45a时,两环距离比较近,线圈磁场的均匀范围和磁感应线如图7所示。鞍点磁场增加为BS=1.516 7B0,磁场的均匀范围左右收缩而上下拉长。B=BS的左右曲线经过原点,B=1.01BS的等值线与B=0.99BS的等值线分别向上下移动而不经过原点,均匀区域仍然呈现“八爪”形状,范围稍微缩小。
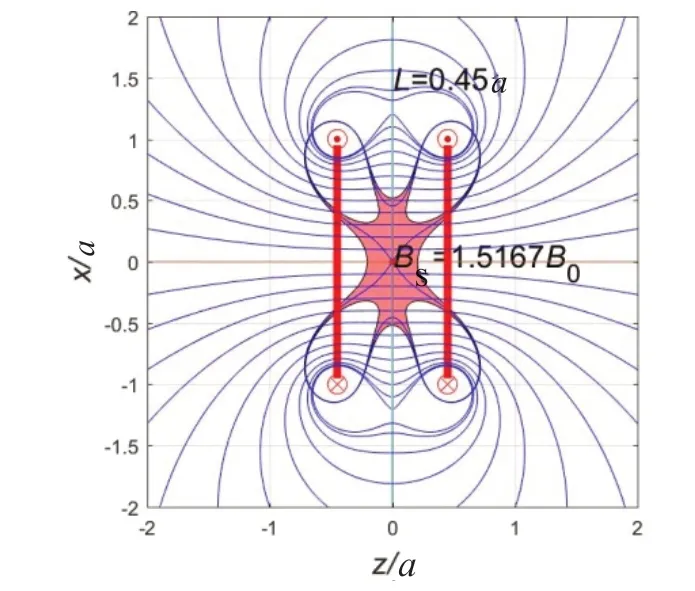
图7 磁场的均匀范围和磁感应线(L=0.45a)
(3)当L=0.4a时,两环距离更加小,磁场的均匀范围和磁感应线如图8所示。鞍点磁场增加为BS=1.600 8B0,B=1.01BS的曲线合并成上下两条曲线,分别包围上面两个电流和下面两个电流,上下各有一个小小的均匀区域,中间均匀区域呈“四爪”形状,上下一对“爪”分别包围上下两个电流。虽然鞍点的磁场增强了,但是均匀区域变得更小了。如果距离继续变小,磁场均匀区域会变得更小而形状不变(图略)。
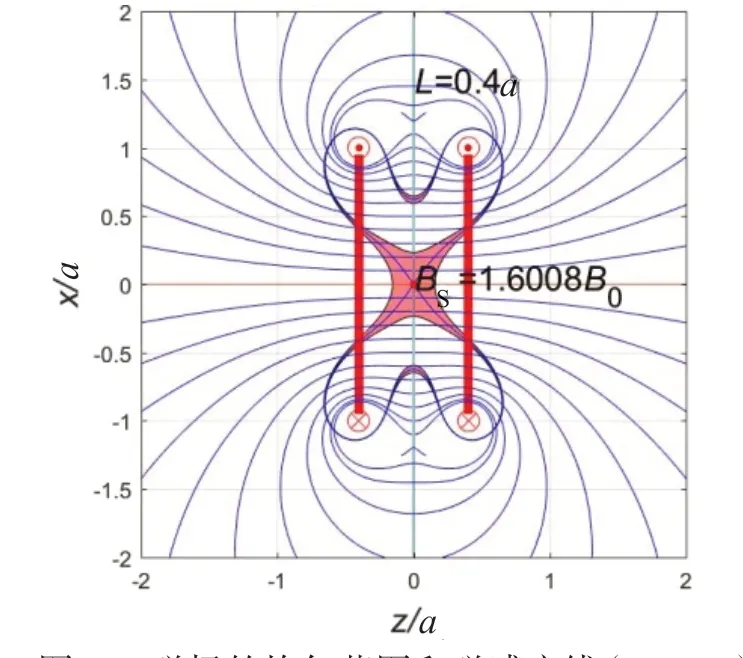
图8 磁场的均匀范围和磁感应线(L=0.4a)
(4)当L=0.55a时,两环距离比较大,线圈磁场的均匀范围和磁感应线如图9所示。鞍点磁场减小为BS=1.3454B0,磁场的均匀范围上下收缩而左右拉长。B=BS的上下曲线经过原点,但是左右部分曲线分别向左右移动而不经过原点,均匀区域仍然呈现“八爪”形状,范围稍微缩小。
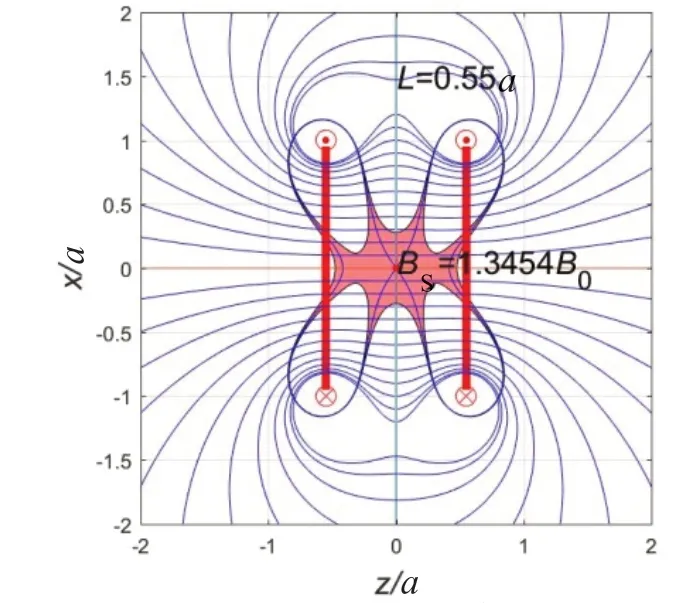
图9 磁场的均匀范围和磁感应线(L=0.55a)
(5)当L=0.6a时,两环距离更大,磁场的均匀范围和磁感应线如图10所示。鞍点磁场减小为BS=1.261B0,B=1.01BS的曲线合并成右边两条曲线,分别包围左边两个电流和右边两个电流,左右各有一个小小的均匀区域,中间均匀区域呈“四爪”形状,左右一对“爪”分别包围左右两个电流。鞍点的磁场减弱了,均匀区域也变得更小了。如果距离继续变大,磁场均匀区域会变得更小而形状不变(图略)。
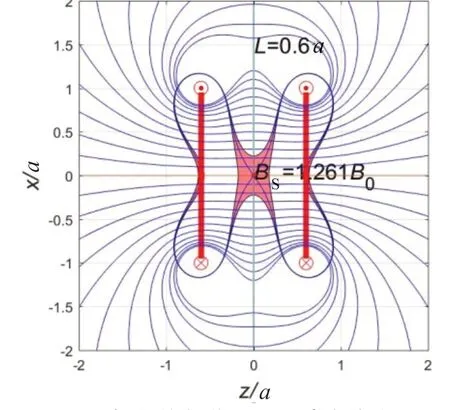
图10 磁场的均匀范围和磁感应线(L= 0.6a)
4 结束语
文章说明了亥姆霍兹线圈在直角坐标系中磁感应强度的解析式,将公式无量纲化,绘制出了亥姆霍兹线圈磁场的分量和合磁场的分布曲面。文章精确地绘制了亥姆霍兹线圈均匀磁场的分布范围和磁感应强度分布线,说明了两环之间的距离对均匀范围的影响。为了提高读者应用MATLAB解决问题的能力,文章附录提供两个完整的主程序和函数文件供读者参考。
附录1
ring2B1main.m
%亥姆霍兹线圈磁场的主程序
clear,l=0.5;%清除变量,距离
ring2B1fun(l)%调用函数文件
ring2B1fun(0.25)%调用函数文件
ring2B1fun(1)%调用函数文件
ring2B1fun.m
%亥姆霍兹线圈的磁场的函数文件
function fun(l)
rm=2;r=linspace(-rm,rm,40);%最大坐标,坐标向量(绕过奇点)
[X,Z]=meshgrid(r);R1=sqrt((Z-l).^2+(abs(X)+1).^2);%坐标矩阵,最大距离
KK1=4*abs(X)./R1.^2;[K1,E1]=ellipke(KK1);%模数,两个完全椭圆积分
Bx1=((1+X.^2+(Z-l).^2)./((abs(X)-1).^2+(Z-l).^2).*E1-K1).*(Z-l)./X/pi./R1;%B的x分量
Bz1=((1-X.^2-(Z-l).^2)./((abs(X)-1).^2+(Z-l).^2).*E1+K1)/pi./R1;%B的z分量
R2=sqrt((Z+l).^2+(abs(X)+1).^2);%最大距离
KK2=4*abs(X)./R2.^2;[K2,E2]=ellipke(KK2);%模数,两个完全椭圆积分
Bx2=((1+X.^2+(Z+l).^2)./((abs(X)-1).^2+(Z+l).^2).*E2-K2).*(Z+l)./X/pi./R2;%B的x分量
Bz2=((1-X.^2-(Z+l).^2)./((abs(X)-1).^2+(Z+l).^2).*E2+K2)/pi./R2;%B的z分量
Bx=Bx1+Bx2;Bz=Bz1+Bz2;%合磁场的x分量,z分量
B=sqrt(Bz.^2+Bx.^2);A=atan2(Bx,Bz);%合磁场,磁场角度
BC={Bz,Bx,B,A};%数据元胞
zc={’itB_z/B m_0’,’itB_x/B m_0’,...
’itB/B m_0’,’italpha m’};%竖坐标元胞
tc={’itz m分量’,’itx m分量’,’总量itB m’,’方向’};%标题的一部分
txt=’itB m_0=itmu m_0itI m/2ita’;%磁感应强度单位文本
t=’亥姆霍兹线圈’;%标题
if l==0.5,t=[t,’临界’];end,fs=16;%如果距离为0.5,修改标题,结束循环,字体大小
for i=1:4,figure%循环,创建图形窗口
surf(Z,X,BC{i}),box on%画曲面,加框
title([t,’磁感应强度的’,tc{i},’的分布面(itL m=’,...
num2str(l),’ita m)’],’FontSize’,fs)%显示标题
xlabel(’itz/a’,’FontSize’,fs)%显示x坐标
ylabel(’itx/a’,’FontSize’,fs)%显示y坐标
zlabel(zc{i},’FontSize’,fs)%显示z坐标
end,view(-45,60)%结束循环,设置角度曲面的视角
附录2
ring2B2main.m
%亥姆霍兹线圈均匀区域的主程序
clear,l=0.5;%ring2B2fun(l)%清除变量,距离,调用函数文件
ring2B2fun(0.45)%调用函数文件
ring2B2fun(0.4)%调用函数文件
ring2B2fun(0.55)%调用函数文件
ring2B2fun(0.6)%调用函数文件
ring2B2fun.m
%亥姆霍兹线圈的磁场均匀区域的范围的函数文件
function fun(l)
rm=2;r=linspace(-rm,rm,200);%最大坐标,坐标向量(绕过奇点)
[Z,X]=meshgrid(r);R1=sqrt((Z-l).^2+(abs(X)+1).^2);%坐标矩阵,最大距离
KK1=4*abs(X)./R1.^2;[K1,E1]=ellipke(KK1);%模数,两个完全椭圆积分
Bx1=((1+X.^2+(Z-l).^2)./((abs(X)-1).^2+(Z-l).^2).*E1-K1).*(Z-l)./X/pi./R1;%B的x分量
Bz1=((1-X.^2-(Z-l).^2)./((abs(X)-1).^2+(Z-l).^2).*E1+K1)/pi./R1;%B的z分量
R2=sqrt((Z+l).^2+(abs(X)+1).^2);%最大距离
KK2=4*abs(X)./R2.^2;[K2,E2]=ellipke(KK2);%模数,两个完全椭圆积分
Bx2=((1+X.^2+(Z+l).^2)./((abs(X)-1).^2+(Z+l).^2).*E2-K2).*(Z+l)./X/pi./R2;%B的x分量
Bz2=((1-X.^2-(Z+l).^2)./((abs(X)-1).^2+(Z+l).^2).*E2+K2)/pi./R2;%B的z分量
Bx=Bx1+Bx2;Bz=Bz1+Bz2;B=sqrt(Bz.^2+Bx.^2);%合磁场的x分量,z分量,合磁场
m=3;B(B>m)=m;fs=16;%截断磁场,大于截断磁场者取截断磁场,字体大小
t=’亥姆霍兹线圈’;%标题
if l==0.5,t=[t,’临界’];end %如果距离为0.5,修改标题,结束循环
figure,surf(Z,X,B)%开创图形窗口,画B解析解的网格曲线
shading interp,alpha(0.8)%染色,半透明
bs=2/(1+l^2)^(3/2);hold on%原点磁场,保持属性
contour3(Z,X,B,[1,1]*bs,’b’)%画中等值线
C1=contour3(Z,X,B,[0.99,0.99]*bs,’r’);%画下等值线取坐标
C2=contour3(Z,X,B,[1.01,1.01]*bs,’k’);%画上等值线取坐标
title([t,’的合磁场(itL m=’,num2str(l),’ita m)’],’FontSize’,fs)%显示标题
xlabel(’itz/a’,’FontSize’,fs)%显示x坐标
ylabel(’itx/a’,’FontSize’,fs)%显示y坐标
zlabel(’itB/B m_0’,’FontSize’,fs)%显示z坐标
view(-45,45),box on%设置视角,加框
plot3(0,0,bs,’r.’,’MarkerSize’,10)%画原点磁场
txt=[’itL m=’,num2str(l),’ita m’];%距离字符串
text(0,0,m,txt,’FontSize’,fs)%显示距离
x1=C1(1,2:end);y1=C1(2,2:end);%取下线横,纵坐标
n=C2(2,1);x2=C2(1,2:1+n);y2=C2(2,2:1+n);%上线坐标对数,取上线坐标
figure,fill(x1,y1,’r’)%开创图形窗口,画下线填色图
alpha(0.5),hold on%平面半透明,保持属性
fill(x2,y2,’w’),fill(x2,-y2,’w’)%画左下方上线,左上方上线白色图
fill(-x2,-y2,’w’),fill(-x2,y2,’w’)%画右上方上线,右下方上线白色图
contour(Z,X,B,[1,1]*bs,’b’)%画等值线
plot([0;0],[-rm;rm]),plot([-rm;rm],[0;0])%画竖直轴线,画水平轴线
ms=10;%符号大小
plot(l,1,’ro’,l,1,’r.’,’MarkerSize’,ms)%画右边流出屏幕的电流
plot(l,-1,’ro’,l,-1,’rx’,’MarkerSize’,ms)%画右边流进屏幕的电流
plot(-l,1,’ro’,-l,1,’r.’,’MarkerSize’,ms)%画左边流出屏幕的电流
plot(-l,-1,’ro’,-l,-1,’rx’,’MarkerSize’,ms)%画左边流进屏幕的电流
plot([l,l],[-1+0.05;1-0.05],’r’,’LineWidth’,4)%画右环的剖面
plot([-l,-l],[-1+0.05;1-0.05],’r’,’LineWidth’,4)%画左环的剖面
sx=0.1:0.1:1.2;sz=0*sx+0.01;%磁感应线的起点纵,横坐标
Bx(Z<=-0.1)=NaN;%左边Bx值改为非数
streamline(Z,X,Bz,Bx,sz,sx)%画第一象限磁感应线
streamline(-Z,X,-Bz,Bx,-sz,sx)%画第二象限磁感应线
streamline(Z,-X,Bz,-Bx,sz,-sx)%画第三象限磁感应线
streamline(-Z,-X,-Bz,-Bx,-sz,-sx)%画第四象限磁感应线
plot(0,0,’r.’,’MarkerSize’,10)%画原点
title([t,’合磁场的均匀范围’],’FontSize’,fs)%显示标题
xlabel(’itz/a’,’FontSize’,fs)%显示x坐标
ylabel(’itx/a’,’FontSize’,fs)%显示y坐标
grid on,axis equal%加网格,使坐标刻度相等
text(0,1.5,txt,’FontSize’,fs)%显示距离
if l==0.5%如果距离为0.5
text(0,0,[’itB m_C=’,num2str(bs),’itB m_0’],’FontSize’,fs)%显示鞍点磁场值
else%否则
text(0,0,[’itB m_S=’,num2str(bs),’itB m_0’],’FontSize’,fs)%显示鞍点磁场值
end%结束循环

