考虑航天器钟差影响的增广脉冲星方位误差估计算法

王宏力，张鹏飞，何 星，冯 磊，肖永强

(1.火箭军工程大学 导弹工程学院， 西安 710025；2.西安建筑科技大学 信息与控制工程学院， 西安 710055)

1 引言

X射线脉冲星导航具有自主性强、可靠性高的特点，在各领域有着巨大的发展前景[1-2]。然而在脉冲星导航过程中，脉冲星方位误差会对导航精度造成严重的影响，通常0.001″的方位误差就会造成几百米的定位误差[3]。由于脉冲信号微弱以及测量方法和设备的限制，目前常用的甚长基线干涉测量技术(very long baseline interferometry，VLBI)难以满足导航精度的要求。因此，为了提高脉冲星方位误差估计精度，国内学者采用了基于信标卫星的估计[4-5]、鲁棒滤波估计[6-7]、组合导航[8]等方法对脉冲星方位误差进行估计，没有考虑航天器的时钟钟差的影响。孙守明、王璐等研究了脉冲星导航以及脉冲星与惯性、多普勒等组合导航中的钟差修正问题[9-10]，对于脉冲星方位误差估计过程中的钟差修正问题尚缺乏研究。当利用信标卫星进行脉冲星方位误差估计时，由于航天器长时间运行，时钟钟差会发生单向漂移，进而会造成系统偏差，从而使脉冲星方位误差估计精度降低。本文中设计了考虑航天器钟差影响的增广脉冲星方位误差估计算法，消除脉冲星方位误差估计时航天器时钟钟差影响，提高脉冲星方位误差的估计精度。

2 脉冲星方位误差估计的传统模型

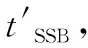
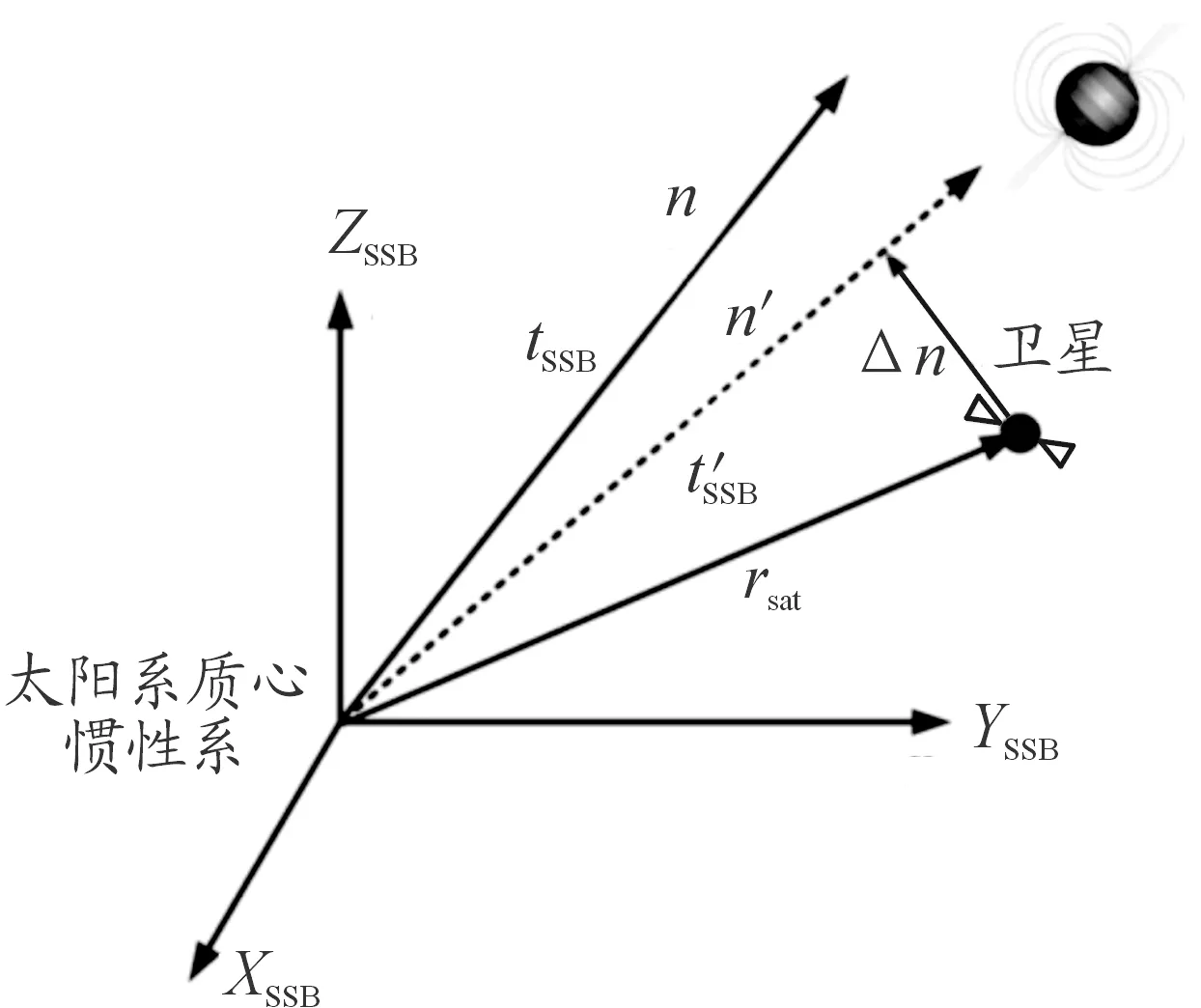
图1 脉冲星方位误差估计原理示意图Fig.1 The principle of azimuth error estimation of pulsar

转换过程公式为[12]：

(1)

(2)

式(2)中：tsat为脉冲到达卫星的真实时间；n为真实的脉冲星单位方向矢量。设脉冲星的赤经为α，赤纬为β，则满足：

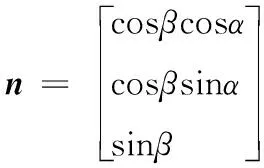
(3)

设(Δα，Δβ)为脉冲星方位误差，则真实的脉冲星方位与带误差的脉冲星方位满足：

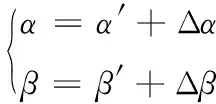
(4)

将式(4)代入式(3)，进行泰勒展开并忽略二阶及以上小项可得：

n=n′+Δn

(5)

其中，带误差的脉冲星方向矢量为：

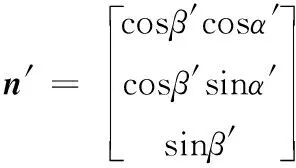
(6)

脉冲星单位方向矢量误差Δn为：

(7)

(8)

(9)

(10)

传统算法未考虑航天器时钟长期运行，时钟钟差缓变对脉冲星方位误差影响，一般精度为10 mas左右，因此有必要对航天器时钟钟差进行修正。

3 时钟钟差对脉冲星方位误差估计精度影响分析

由于信标卫星时钟频率和相位的漂移，脉冲到达卫星的真实时间和卫星时钟测得的脉冲到达时间之间存在钟差，设其为δt，则满足：

(11)

此时：

(12)

卫星时钟钟差模型可写为[13]：

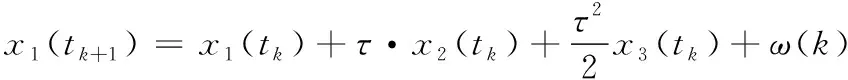
(13)

式(13)中：x1、x2和x3分别为钟差、钟差漂移率和钟差漂移率的变化率；τ为时间间隔；ω为高斯白噪声，其方差矩阵为：

Q(τ)=E[ω(k)ω(k)T]=

(14)

其中，q1、q2和q3为噪声的功率谱密度。其离散过程模型可写为：

(15)

取钟差漂移率为3.637 979×10-12，根据铷原子钟模型，取时钟的噪声谱密度分别为q1=1.11×10-22s和q2=2.22×10-32s。给定时钟初始时刻的钟差为0 s，取时间间隔为1 s，则可得到钟差随时间的变化如图2所示。

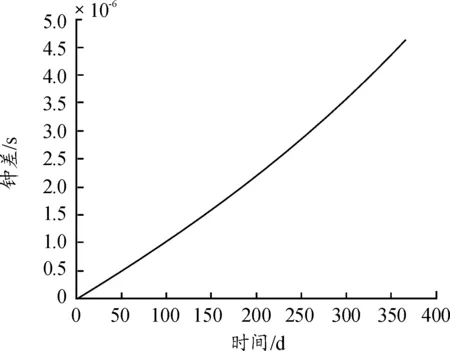
图2 钟差随时间变化曲线Fig.2 Clock difference changes with time

由图2可得，钟差特点一是单向观测，无法通过双向观测消除钟差影响，二是缓慢增大。虽然钟差增长缓慢，但随着时间的推移，钟差接近5×10-6s，该值与光速相乘理论上会造成1 500 m左右的定位误差，将会给系统造成不可忽略的影响。因此，为分析其对方位误差估计的影响，使用传统脉冲星方位误差估计算法进行仿真。以脉冲星B0531+21作为观测脉冲星，其参数如表1所示。

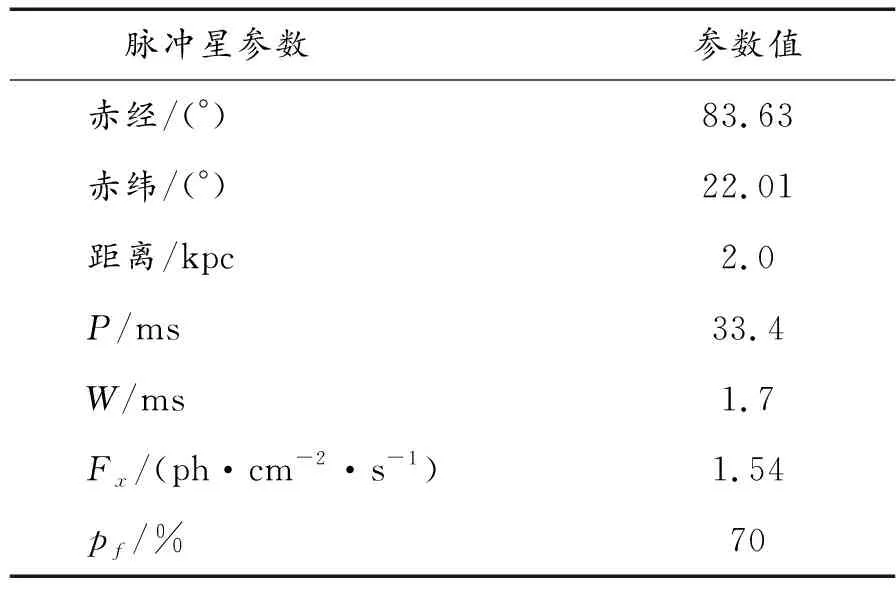
表1 脉冲星B0531+21参数

表1中，P为脉冲周期，W为脉冲宽度，Fx为脉冲辐射光子流量，pf为一个脉冲周期内脉冲辐射流量与平均辐射流量之比。脉冲星的观测噪声方差可由式(16)计算得到[14]，即

(16)

式(16)中：A为探测器有效面积，本仿真中设为1 m2；Bx=0.005 ph·cm-2·s-1，为宇宙背景噪声；d为脉冲宽度W与脉冲周期P之比；tobs为观测时间，设为1 000 s。则可计算得到σ=(77.69 m)2。脉冲星方位误差设为(2 mas，2 mas)，初始状态设为0。

使用同一颗卫星，分别在有无钟差影响的情况下进行仿真，卫星轨道参数如表2所示。

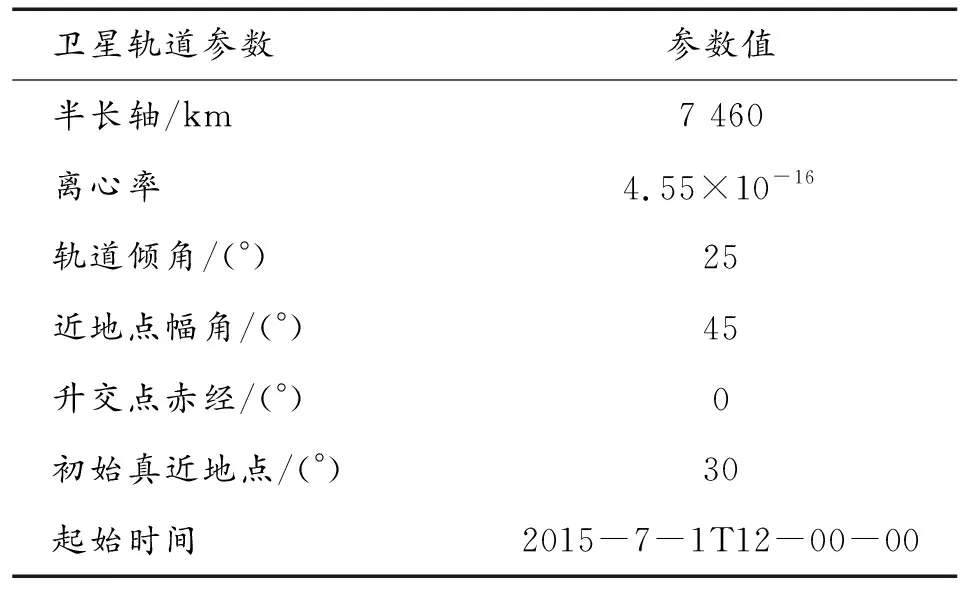
表2 卫星轨道参数

仿真结果如图3所示。

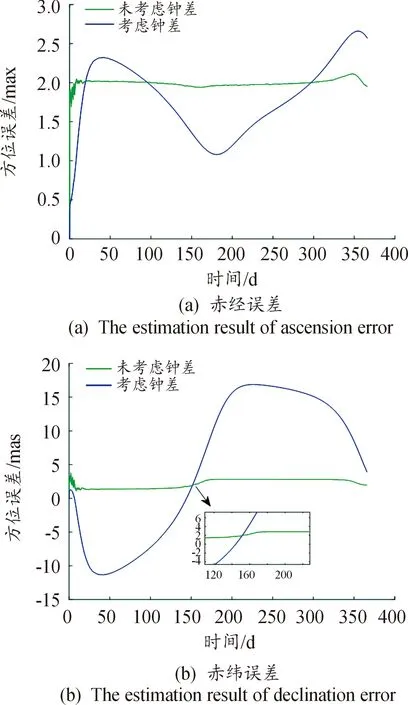
图3 有无钟差的脉冲星方位误差估计曲线Fig.3 The azimuth error estimation results of pulsars with or without clock errors

对比分析图3可得，当无钟差影响时，传统脉冲星方位误差估计算法能较为精确地估计方位误差。但当存在钟差时，估计结果误差较大，尤其是赤纬误差，接近17 mas；而且赤经和赤纬误差估计结果都没有收敛到一个定值。可见，时钟钟差会对脉冲星方位误差估计精度产生较大的影响，因此有必要对卫星时钟钟差进行修正。

4 增广钟差脉冲星方位误差估计算法

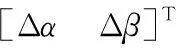
Xk+1=AkXk+Wk

(17)

(18)

由于该系统是线性时变系统，因此采用PWCS可观性判据分析其可观性，将系统分为j个时间段，在每个时间段里认为其为线性定常系统。

系统总的可观测性矩阵为：

(19)

第j个时间段的可观测矩阵为：

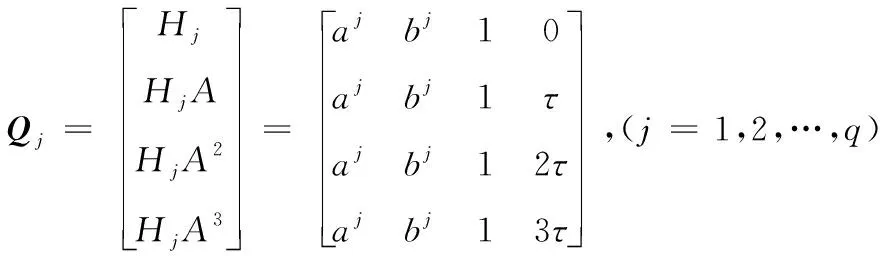
(20)

其中：

(21)

其中任意相邻的3个时间段满足：

(22)

对其中任意相邻的3个时间段进行初等变换可得：

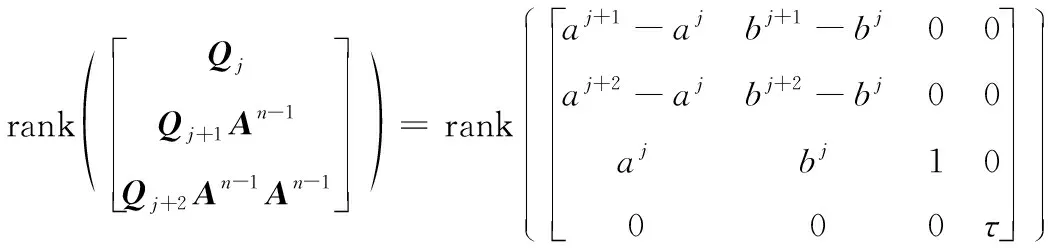
(23)

由于τ>0且卫星在运行过程中相邻3个点一般不在一个平面内，因此：

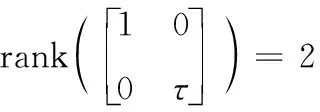
(24)

(25)

进而可得：

(26)

因此该系统完全可观测。

仿真条件不变，根据该增广算法，利用卡尔曼滤波进行最优估计，估计结果如图4和图5所示。

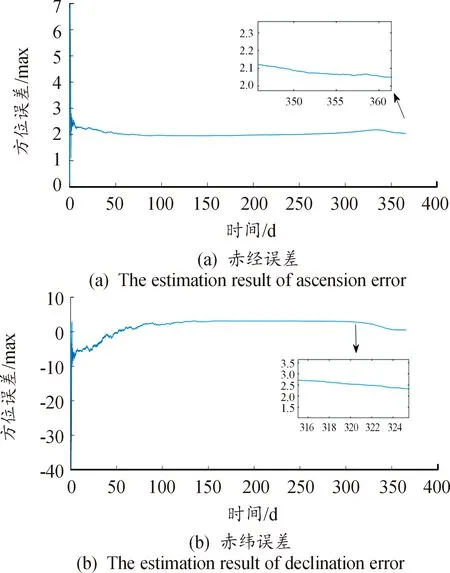
图4 ASKF算法估计曲线Fig.4 ASKF algorithm estimation results

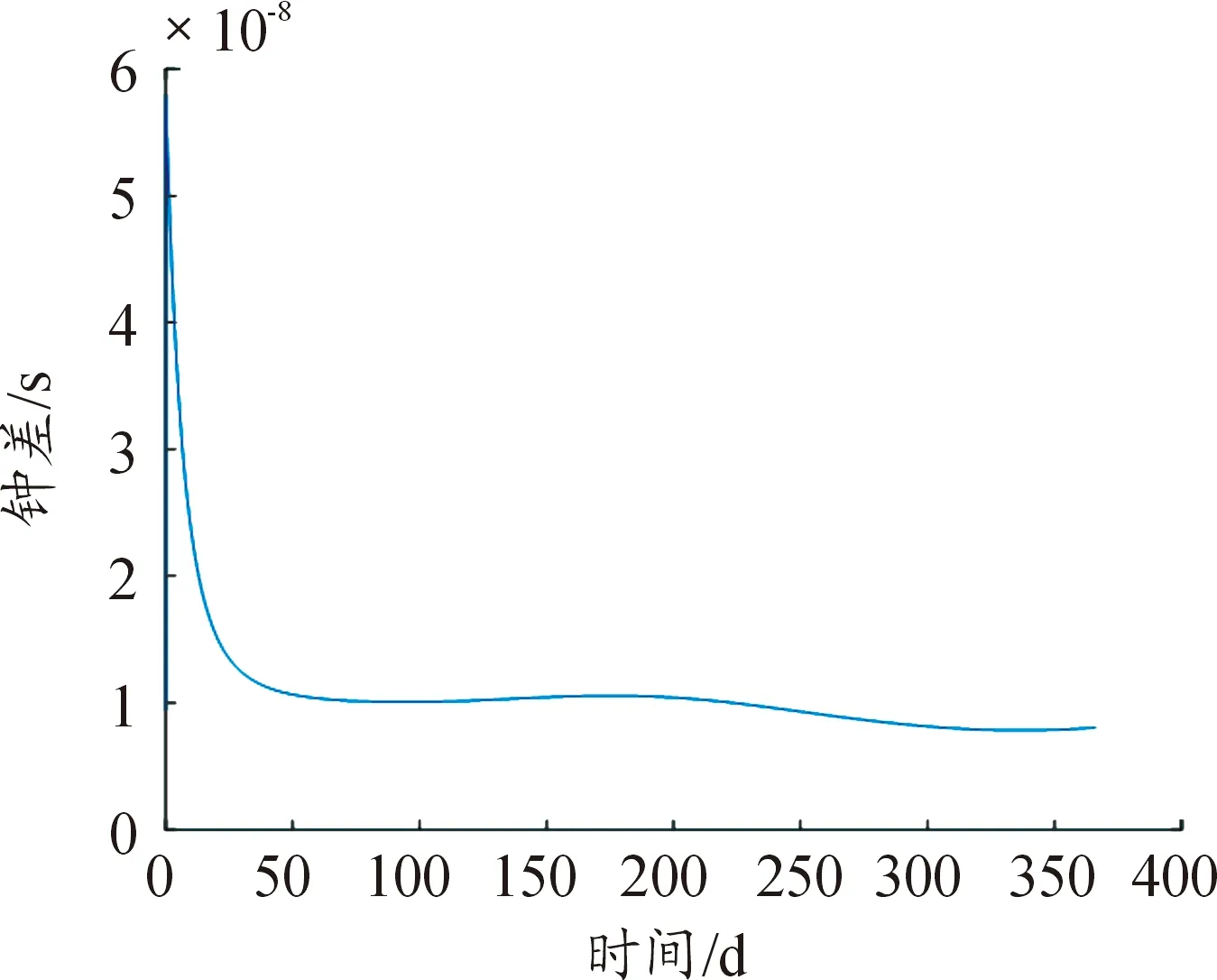
图5 修正后的钟差Fig.5 The corrected clock error

其他条件不变，设置不同的钟差来验证所提算法的有效性，如表3所示。

为进一步验证该增广算法的有效性，钟差、脉冲星方位误差初始值以及卫星轨道参数等保持不变，选用不同的脉冲星进行仿真验证，脉冲星参数如表4所示。估计结果如表5所示。

由上述图表可知，当存在钟差影响时，传统算法没有修正钟差，估计结果发散且偏差较大。而本文提出的考虑钟差影响的增广脉冲星方位误差估计算法估计结果均能收敛，估计精度也较高，使赤经和赤纬估计精度分别保持在0.1 mas和0.3 mas左右，且经该增广算法修正后，能有效抑制钟差发散，使时钟钟差大小约减小2个数量级，能有效隔离钟差的影响。而且当钟差大小不同、对于不同的脉冲星，本文所提出的增广算法均能克服钟差影响，使估计结果保持较高的估计精度。

5 结论

1) 利用信标卫星进行脉冲星方位误差估计时，信标卫星的时钟钟差会造成系统偏差，对估计结果产生影响，且不容忽略，必须修正才能提高估计精度。

2) 本文中提出的考虑钟差修正的增广脉冲星方位误差估计算法能有效隔离时钟钟差的影响，在保证滤波解算稳定性的同时，使估计精度保持在无钟差影响水平。