The Optimal Matching Parameter of Half Discrete Hilbert Type Multiple Integral Inequalities with Non-Homogeneous Kernels and Applications

(1.Department of Applied Mathematics, Guangzhou Huashang College, Guangzhou 511300, China;2.Department of Mathematics, Guangdong University of Education, Guangzhou 510303, China.)

Abstract: By using the weight function method, the matching parameters of the half discrete Hilbert type multiple integral inequality with a non-homogeneous kernel K(n,||x||ρ,m) = are discussed, some equivalent conditions of the optimal matching parameter are established, and the expression of the optimal constant factor is obtained.Finally, their applications in operator theory are considered.

Keywords: Non-homogeneous kernel; Half discrete Hilbert type multiple integral inequality; Best constant factor; Optimal matching parameter; Operator norm; Bounded operator

§1.Introduction

and the constantis optimal.Afterwards, [1,4,16]discussed such Hilbert type inequalities with non-homogenous kernel.Base on these work, in this paper, we will study a wider class of half discrete Hilbert type multiple integral inequalities with nonhomogeneous kernels.

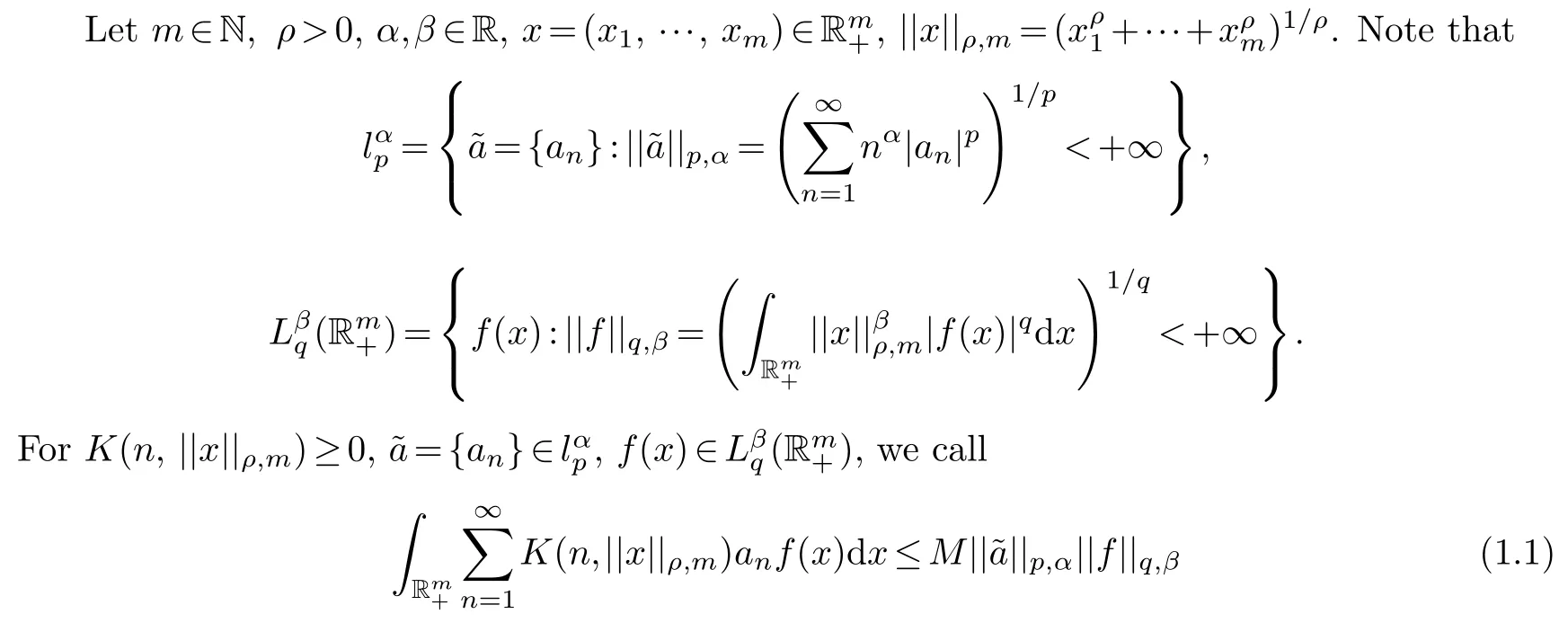
half discrete Hilbert type multiple integral inequality.If we define series operatorT1and integral operatorT2respectively:

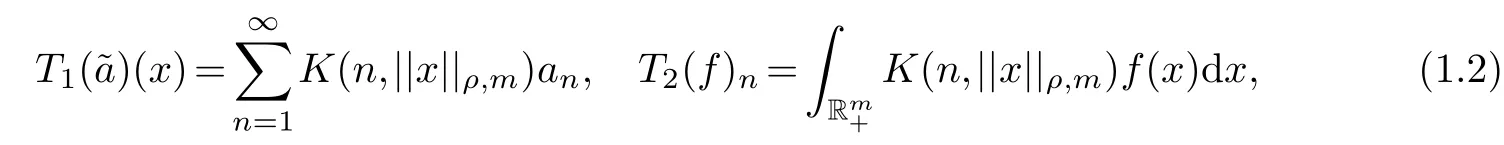
thenT1can be a mapping from spacelto spaceL, andT2can be a mapping from spaceLto spacel.By the basic theories of Hilbert type inequality, (1.1) is equivalent to the following operator inequality:

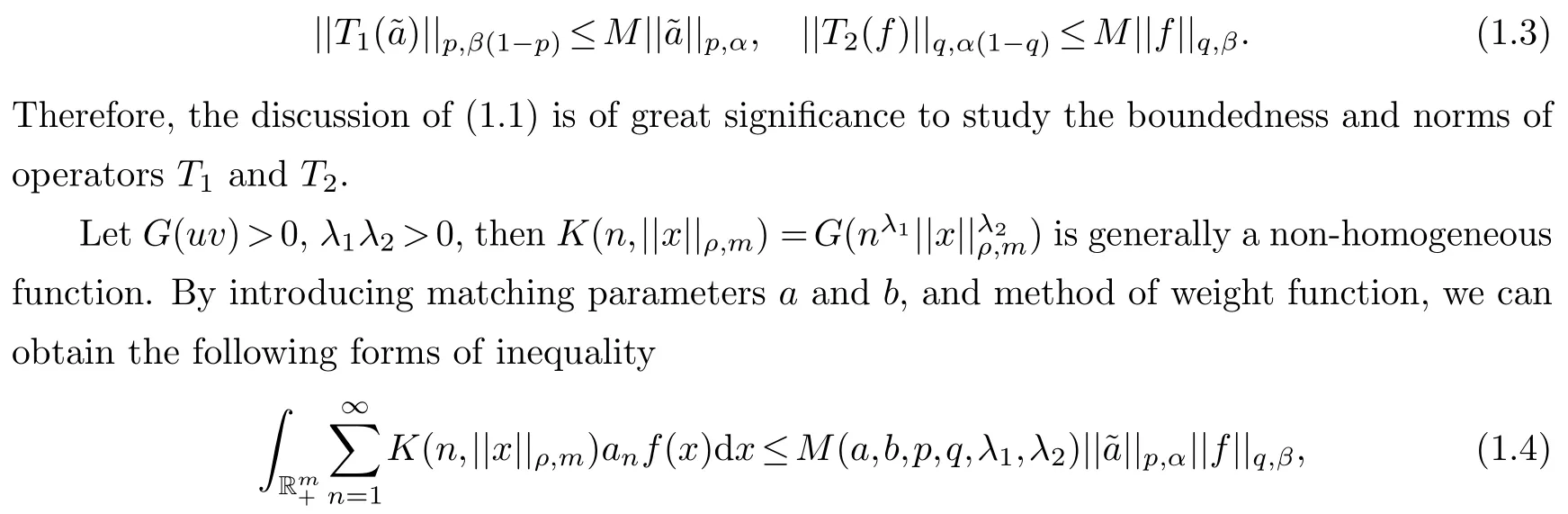
whereα, βdepend ona, b, p, q, λ1andλ2.Generally speaking, the constant factorM(a,b,p,q,λ1,λ2) is not optimal.As long as the parameters meet certain conditions, it is possible to makeMthe best value.If there existaandbsuch thatMof (1.1) is optimal, thena, bare called the best matching parameters.

At present, although many Hilbert type inequalities with optimal constant factors have been obtained in [5–14]at home and abroad, the basic conditions for the optimal matching parameters of (1.4) have not been completely solved.The purpose of this paper is to discuss the basic characteristics of optimal matching parameters for non-homogeneous kernelK(n,||x||ρ,m)=and obtain some equivalent conditions.

§2.Some lemmas

Lemma 2.1.[2]Assume that pi ≥0, ai ≥0, αi ＞0(i=2, ···, n), ψ(u)is measurable.Then

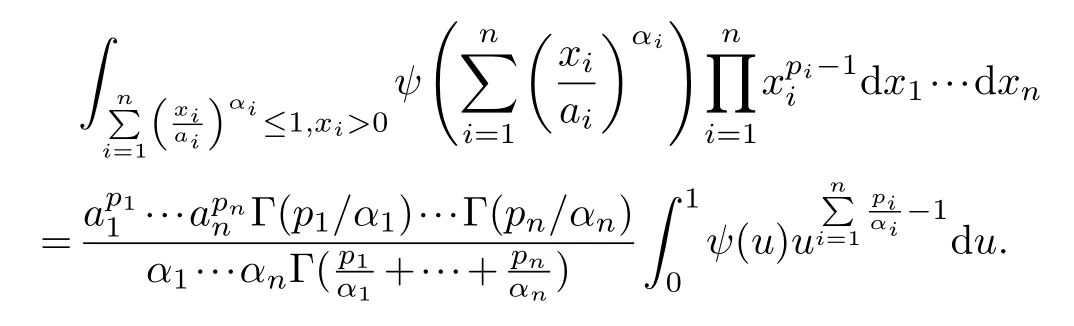
By using lemma 2.1, it is not difficult to obtain the following lemma.

Lemma 2.2.Suppose that m∈N, ρ＞0, x=(x1, ···, xm)∈Rm+, φ(t)is measurable, r ＞0.Then

§3.Main results and proofs

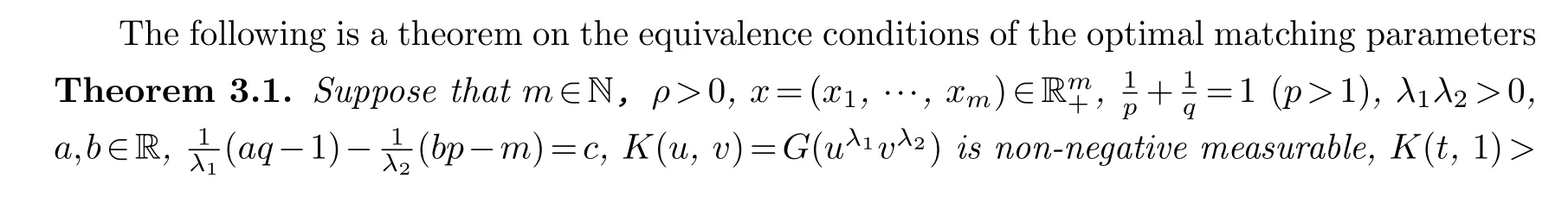
For sufficiently smallε＞0 and sufficiently large natural numberN, take

Letε→0+and thenN →+∞, the quadratic limit is

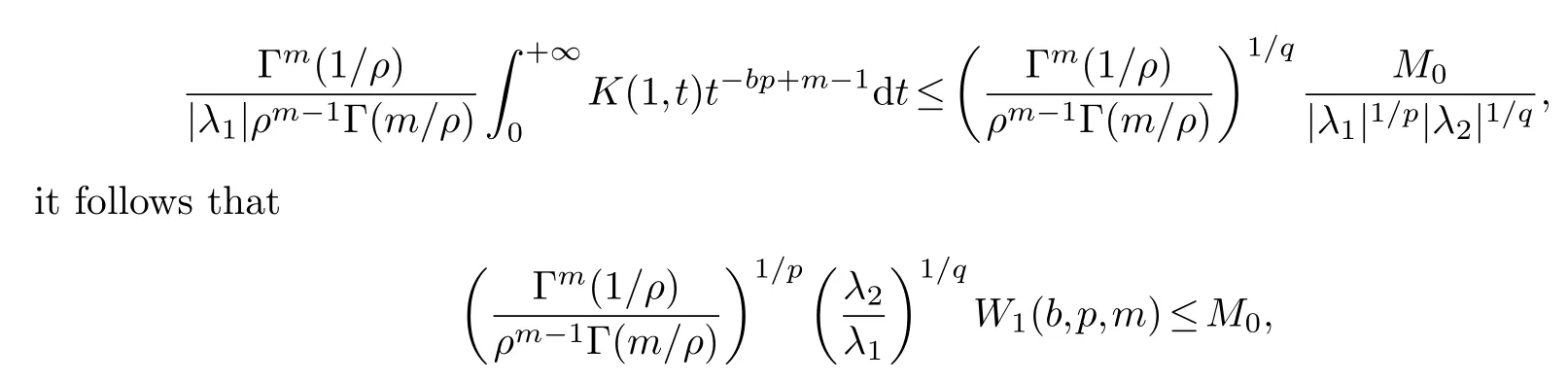
this is in contradiction with (3.3).Hence the constant factor of (3.2) is the best, and the same as (3.1).

Therefore,

§4.Applications in operator theory

Note the equivalence of (1.1) and (1.3), according to Theorem 3.1, the following equivalent theorem can be obtained.