基于LRWD轮廓系数的社团检测新方法

孟 雪，许 英

(新疆财经大学 统计与数据科学学院，乌鲁木齐 830012)

社团检测技术广泛应用于社会网络、引用网络、食品网络、生物网络等多个领域[1]。 在社团中，人们通常理解节点的子集与网络的其余部分之间的互连更为紧密。利用生物学、物理学、社会科 学、应用数学和计算机科学等不同学科的技术和工具，开发了许多社团检测算法[2]。 在文献[3]中，Newman和Girvan引入了模块度函数Q，通过模块度函数Q，使我们找出网络分解到社团的最佳方式社团。

本文提出了一种基于局部随机游走距离轮廓系数的网络社团检测新算法(Silhouette算法，简记为SIL算法)，并给出一个新的定量函数平均轮廓来评估质量网络社团结构。 同时，通过四个现实世界网络和计算机生成网络(Girvan和Newman[3]提出的GN基准和Lancichineti Andrea等人[4]对GN Benchmark的缺陷提出的LFR基准)进行了测试。 实验结果表明，SIL算法能够以较高的NMI(Normalized Mutual Information)值、模块度和平均轮廓值准确有效地检测网络的社团结构。

1 算法架构

1.1 局部随机游走距离

给定无向无权网络G=(V，E)，其中V是节点集合，E是边集合。随机游走是一个重要的随机过程，它可以表示随机游走者经过的一系列节点。转移概率矩阵P，其中Pij=aij/kj代表在随机游走者i在下一步步行到j的概率。其中A=(aij)是网络的邻接矩阵，ki表示节点的i的度，与其他基于随机游走的距离度量相比，具有较低的时间复杂度。

给定随机游走者i开始，在t步骤之后，该游走者到达j的概率可以用πij(t)表示。这个系统的演变方程可表示为πi(t)=PTπ(t-1)，其初始系统状态为πi(0)=ei，第i个位置为1其他为0.随机游走者访问t步后，LRW(Local Random Walk)指数可以定义如下：

(1)

其中|E|是网络的边数。

SRW(Superposed Random Walk)度量是LRW在t步时间内的叠加，描述了随机游走者从起始节点连续释放，定义为：

(2)

节点i与节点j之间的局部随机游走距离(LRWD)定义如下：

(3)

因此网络的距离矩阵D=(dij)可以根据上述公式计算。以下实验将网络的直径设置为随机步长t，通常是小于n.

1.2 轮廓系数

基于上述局部随机行走距离构造轮廓系数[4]，对于每个节点，将引入一个确定的值s(i)，称为轮廓系数。

将网络G划分为{C1，C2，C3，…，Ck}，其中k是社团的数量。对于网络中的任何节点i，并用gi表示它被分配到的社团。考虑a(i)为节点i和与i同一社团中的其他节点之间的平均距离，这是“内部”距离。

(4)

对于所有其他社团Cl，d(i，Cl)是i与Cl中其他节点之间的平均距离，即“之间”距离。

(5)

在计算了所有社团Cl≠gi的d(i，Cl)之后，选择d(i，Cl)的最小值，通过：

(6)

是节点i与最近社团之间的距离。达到这个最小值的社团B(即d(i，B)=b(i))，称之为节点i的次优选择社团。 因此，了解网络中每个节点的次优选择社团是非常重要的。

轮廓系数s(i)定义为:

(7)

当社团gi只有一个不清楚如何定义的节点a(i)，简单地设置s(i)等于零，-1≤s(i)≤1.

(8)

1.3 算法

从上述轮廓系数和平均轮廓的定义可以看出，对于网络的任何社团结构，都可以用轮廓来判断节点是否分类正确。如果一个节点被错误分类，那么可以将这个节点重新分类为次优选择社团，这将是一个新的网络社团结构。基于这一观点，提出以下算法：

算法：基于LRWD轮廓的社团检测算法

输入：网络G=(V，E)，|V|=n

输出：网络的社团结构

步骤1.根据局部随机游走计算距离矩阵;

步骤2.使用密度峰值方法选择社团中心;

节点i与密度较高的任何其他节点之间的最小距离

(9)

请注意，δi和ρi值异常大的节点为社团中心;

步骤3.计算除社团中心以外的每个节点V到社团中心的距离，将节点划分给距离最小的社团;

步骤4.使用轮廓系数调整社团。对于网络的点v，如果点v的轮廓系数s(v)满足s(v)<0，则将点v分配给次优选择社团，否则，保持点v在原来的社团;

步骤5.重复步骤4，直到网络的社团结构不再改变。(当改变很小时，或者在最大的迭代次数之后，停止重复)

1.4 复杂度

SIL算法的时间复杂度O(n2)+O(nkt)，在第一部分中，选择社团中心的时间复杂度为O(n2)；在第二部分中，根据距离将每个节点分配给社团的时间复杂度为O(nk)，O(nkt)是基于轮廓系数更新社团结构的后续迭代过程的时间复杂度，其中k是社团中心的数目，t是迭代时间。

2 应用

本节使用三个真实世界网络和计算机生成网络以评估所提出算法的性能。 使用的真实世界网络包括空手道俱乐部网络、海豚络和NCAA足球网络。

2.1 真实网络检测

A.空手道俱乐部网络

空手道俱乐部网络由34个节点和78条边组成，该网络被分成两个社团。根据密度峰值方法选择k=2,3,4个社团中心(图1(b))，利用SIL算法对网络进行划分，不同k的平均轮廓值为:

(10)

根据平均轮廓的含义，空手道网络分为2个社团是最佳选择。在图1(a)中，采用该算法检测空手道网络的社团结构与实际社团结构相同。

图1 空手道俱乐部网络社团结构部分

B.海豚网络

海豚网络由62个节点和159条边组成，该网络具有两个社团。我们根据密度峰值方法选择了k=2，3，4个社团中心(图2(b))利用SIL算法进行网络划分，不同k的平均轮廓值是:

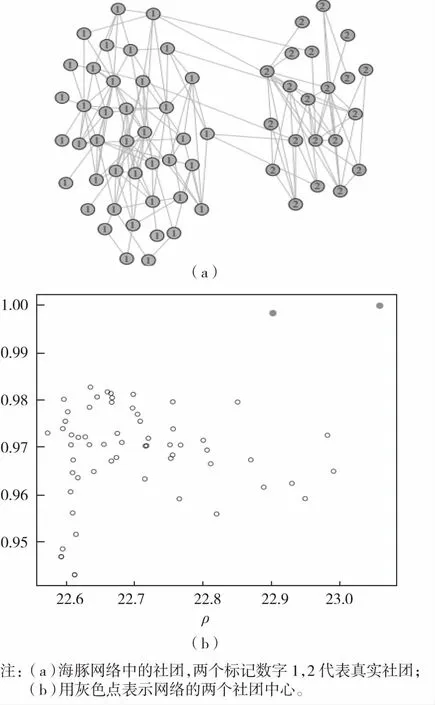
图2 海豚网络社团结构划分

(11)

显然，海豚网络的最佳社团数量是k=2.图2(b)中，实际社团数字1和2的数字，该算法识别了两个颜色不同的社团，与实际的两个社团是相同的。

C．NCAA足球网络(National Collegiate Athletic Association)

D．NCAA足球网络由115个节点和613条边组成,该网络被分成十二个社团。利用SIL算法对不同数量的社团k=8，9，10，11，12进行社团划分，并计算平均轮廓系数

(12)

图3 足球网络社团结构划分

根据表1和表2，在这三个现实世界的网络中，模块度函数的值并不是最大的，但是在实际社团划分的归一化互信息表明，本文的算法可以检测到更真实的社团结构。所提出的算法，三个网络的平均轮廓要比其他三个算法大，更接近网络的真实社团结构。

表1 三个真实世界网络在四种算法下的NMI值和社团数k

表2 三个真实世界网络在四种算法下的Q值和平均轮廓值

2.2 计算机生成网络检测

A.GN基准

Girvan和Newman[3]给出128个节点计算机生成的网络，称为GN人工网络。网络由128个节点组成，分别属于4个大小相等的社团，每个社团包含32个节点。每个节点的平均度〈k〉为16，并且边被独立随机放置在节点对之间，其概率取决于两个节点是否属于同一个社团。每个节点都有与同一个社团中的其他节点连接的平均连接边kin，以及社团之间的边kout，并且kin+kout=16.随着kout从零的增长，网络中的社团变得越来越难以发现。

图4(a)可以看到，四种算法的社团检测结果NMI，当kout<8时，该算法有利于发现合理的社团。当kout=8时，注意到FG和LE算法不能发现合理的社团，本文的算法比LE和FG表现更好，但比SP差。当kout>8时，在GN网络中，社团结构不合理，因此所有算法都无法发现社团结构。如图4所示，当kout<8时，图4(b)(c)，所提出的算法SIL的模块度和平均轮廓是四种算法中最大的。

图4 GN网络中不同算法NMI、模块度平均轮廓比较

B.LFR基准

根据LFR基准，通过设置不同的幂律分布规则来生成的网络，这些网络更接近现实的网络。为了验证LFR准则的SIL算法的效率，设置不同的参数，生成了五个不同规模的网络，节点N=100～1 000.

根据表3，在某些LFR基准中，SIL算法得到的社团结果比FG，LE和SP算法得到的社团更准确，SIL算法可以有效地得到由LFR基准生成的不同规模测试网络中的社团。

表3 LFR网络在四种算法下的NMI值、模块度值和平均轮廓

3 结论

本文提出了一种基于局部随机游走轮廓系数的社团结构检测算法(SIL算法。 将SIL算法在三个真实世界网络中应用，并在计算机生成的网络(GN基准和LFR基准)上进行了测试，与其他三种算法进行了比较。 实验结果表明，该算法能够有效地识别网络的社团结构。