Dividingcubes算法在数控仿真中的应用
吴涛


摘 要:切削计算是数控仿真系统中的重要组成部分,不同的切削算法直接影响切削效率与切削精度。基于剖分立方体(dividing cubes)算法思想,对体素模型稍作改动,提出了一种新的切削算法。仿真结果表明,基于改进算法的切削面的重绘过程更加简洁,在保证切削精度的同时能有更高的切削效率。但是,由于算法根据毛坯的离散精度的不同,所需要的内存空间也不同,当毛坯的离散精度超过一定程度时,会增加切削计算的计算量,反而降低了切削计算的效率。
关键词:数控仿真;体素模型;剖分立方体;切削计算
中图分类号:TP391.9
文献标志码:A
数控加工过程仿真是数控加工技术与虚拟现实技术相结合的一门技术,其集成了机床数控理论、计算机图形学、计算机辅助制造、计算机辅助设计和建模等相关技术,在虚拟的场景下,对数控设备的加工过程进行全面的仿真。数控仿真采用计算机图形学技术,用动画的方法模拟刀具加工轨迹,可以实时直观地观测到加工过程中每一步的信息,以此验证数字控制程序的正确性,避免在数控加工过程中出现欠切、过切、走空刀,甚至损坏刀具、机床的情况。数控加工過程仿真的核心过程包括工件的三维建模,刀具和毛坯的切削算法以及工件切削面的重绘。
工件的三维实体模型构造方法有很多,如边界表示法、构造实体几何法[1]、八叉树表示法[2]、体素表示法[3]、深度元素法[4]、压缩体素法[5]。
数控加工过程中的切削过程其实是工件和刀具之间的相互作用,在仿真系统中表现为工件实体模型的离散数据与刀具旋转体求交,然后将求交后的数据更新到原来的工件模型的数据结构中,如此不断更新工件的离散数据并实时显示的过程。比较常用的切削计算方法有:工件模型的射线组与刀具运动所形成的扫掠体进行求交计算[6],刀具扫掠体所构造的扫掠面与工件模型上的不规则表面进行曲面之间的求交计算[7-8],基于空间分解的思想将工件模型离散为三角网格进行求交计算[9]等。
切削面的重绘是指在计算出刀具和工件的切削点之后,需要利用相应的切削数据对切削面进行重新绘制,对切削面的重新绘制要求尽可能地接近真实的加工情形。在三维数据场中,常用的可视化算法有移动立方体(marching cubes)算法[10],剖分四面体(marching tetrahedral)算法[11],以及剖分立方体(dividing cubes)算法[12]。
本文基于dividing cubes算法的思想,对原体素模型稍作改动,再结合刀具旋转体模型进行刀具和工件的切削计算,最后对切削面进行重绘。
1 体素模型
体素(voxel)又称体积像素(volume pixel),是可以看作二维像素在三维坐标空间上的扩展,是3D均匀网格组成的结构化数据。每个网格是结构化数据的一个元素,一般称为体素。体素模型是空间划分中最常用的一种方法,本文使用该模型对工件进行建模。
将工件的长、宽、高分别以固定的显示精度在x轴、y轴和z轴上进行离散,其中,nx、ny、nz分别为x轴、y轴和z轴上以固定的精度而离散的单元立方体个数,如图1(a)所示。若将每一个单元立方体作为构造工件模型的最小单位元素,则每一个单元立方体的关键信息元素包含:单元体的索引值(Key,即该体素的右上角顶点的坐标值),单元体是否存在的标志位(isExist,默认为true),如图1(b)所示。
由图1可以看出:体素模型在计算机中可以使用一个三维数组来存储工件模型的相关信息,数组的大小取决于体素模型的离散精度。但是体素模型需要较大的计算机内存空间,而且仿真的精度受离散精度的影响较大。尽管体素模型存在一些缺点,但其采用了静态的数据结构来存储模型的外部及内部数据点的信息,以一定的离散精度为范围求得立方体作为单位,参与材料的去除与模型重构过程,而且还可以用来表示复杂的模型结构。尤其是对立方体工件模型以及简单的刀路轨迹来说,采用体素建模不仅能够提高运算速度,还能降低重构显示的复杂度。
2 刀具旋转体
铣削加工中,通用刀具模型[13]如图2所示。刀具上表面半径
R=r+r2f-(rf-hf)2+(h-hf)tan γ
式中:r为下表面半径;rf为圆角半径;hf为圆角与锥边切点的高度;h为刀具的长度;γ为半锥角。
通过改变以上参数,可以定义不同的刀具:
r=0,rf,hf=rf,γ=0球头刀
r,rf,hf=rf,γ=0圆角刀
r,rf=0,hf=0,γ=0平底刀
其他的刀具模型可以使用类似的方法加入到通用刀具模型中。
刀具旋转体就是刀具在某一时刻沿主轴旋转一周所形成的包络面。刀具的旋转体范围可以根据刀具的轴线方程、母线方程、刀具长度以及刀具半径共同确定。本文主要以平底刀为例,其旋转体可以根据刀具模型的上、下表面和侧表面共同确定,如图3所示。
对于平底刀而言,刀具半径和刀具的上、下表面半径相等,即刀具半径=R(或r)。设刀具刀心点的坐标为O2(x2,y2,z2),刀柄点坐标为O1,刀轴单位轴向量为O2O1(i,j,k),则刀具旋转体的上、下表面及侧表面方程式如下:
Ftop(x,y,z)=i·x+j·y+k·z-
i·(x2+i·h)-
j·(y2+j·h)-
k·(z2+k·h)
Fbase(x,y,z)=i·x+j·y+k·z-
(i·x2+j·y2+k·z2)
Fside(x,y,z)=[(-y2)·k-(z-z2)·j]2+
[(z-z2)·i-(x-x2)·k]2+
[(x-x2)·j-(y-y2)·i]2=R2(1)
在切削计算的过程中,由于毛坯离散后的数据量较大,且每次只有部分数据与刀具旋转体相交,如果遍历全部的离散数据进行切削,显然会大大降低切削计算的效率,因此需要用一定的方法缩小遍历的范围。本文使用刀具包围盒算法[14]来缩小离散数据的遍历范围,以提高切削计算的效率。
3 Dividing cubes算法
Dividing cubes算法[12]是W.E.Lorenson和H.E.Cline于1987年提出的,以体素为基本处理对象。Dividing cubes算法首先对每个体素进行如下分类:
1)所有的8个顶点的值都大于等于等值面的值则为内部体素(interior cube);
2)所有的8个顶点的值都小于等值面的值则为外部体素(exterior cube);
3)其他则为表面体素(surface cube)。
之后,将表面体素在空间上分割为与最终图像解析度相同的子体素(sub cube)。例如,若数据集的规模为256×256×128,而最终显示的窗口的大小为512×512,则在x、y方向上分割一次,在z方向上分割兩次。对每个子体素继续进行分类。对于最终得到的表面体素,计算它的中心点的坐标及法向量,最终形成一个点集,每个点都具有法向量。
Dividing cubes算法实际上是依次扫描每一个体素,当体素与等值面的值相交时,将该体素分割为更小的体素,直到子体素在投影平面上的投影为一个像素大小,然后把所有穿过等值面的子体素作为点投影到平面上。相较于marching cubes算法,dividing cubes算法将绘制的基本元素由三角面片变成了点,无需考虑拓扑结构,实现简单。
4 切削计算
根据dividing cubes算法对表面体素进行分割的思想,将工件离散后的每个体素作如下区分:
1)若体素的8个顶点都在刀具旋转体内部,则该体素被完全切削;
2)若体素的8个顶点都不在刀具旋转体内部,则该体素未被切削;
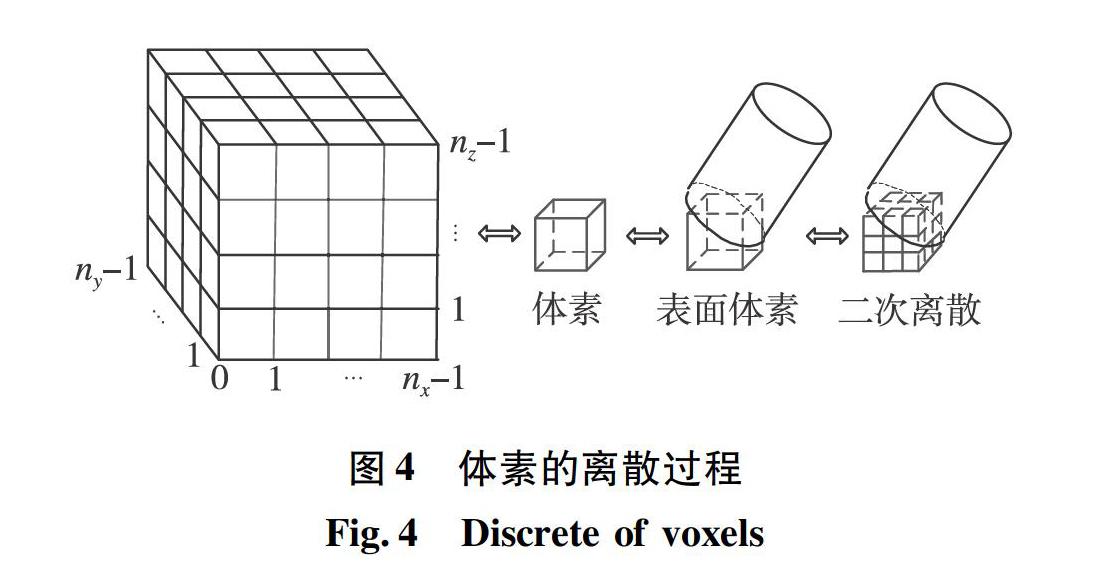
3)若体素的8个顶点中,一部分在刀具旋转体内部,另一部分在刀具旋转体外部,则该体素被部分切削。对于此类体素,进行一定精度的二级离散。
考虑到内存占用的问题,在具体实现的过程中,仅对表面体素进行离散,如图4所示。
在构造数据结构后,对基于体素模型的切削计算也作相应改进。改进后的切削计算算法如下:
步骤1 计算刀具包围盒,判断体素索引是否在刀具包围盒范围之内。如果不在,转入步骤6,否则转入步骤2。
步骤2 根据isExist的值判断体素是否存在。如果不存在,则跳过。如果存在,则将体素的索引坐标值key(x0,y0,z0)带入式(1)中的Fside(x,y,z),若计算结果小于等于刀具半径的平方,即R2,则转入步骤3,否则转入步骤4。
步骤3 结合式(1)中刀具上表面方程Ftop(x,y,z)和下表面方程Fbase(x,y,z),分别计算key(x0,y0,z0)到刀具上表面的距离Dtop和到刀具下表面的距离Dbase。如果h-Dtop-Dbase<ε,则该索引在切削范围之内,转入步骤4,否则转入步骤6。其中:h为刀具长度;ε为允许的误差范围。
步骤4 对一个完整体素的8个顶点的坐标值,依次按照步骤2、3的方法判断其是否在切削范围之内。若该体素的8个顶点都在切削范围之内,则该体素为内部体素,被完全切削,isExist的值为false,转入步骤6;若该体素的8个顶点都不在切削范围内,则该体素为外部体素,未被切削,isExist的值为true,转入步骤6;若该体素的8个顶点中,一部分在切削范围之内,另一部分不在切削范围之内,则该体素为表面体素,被部分切削,isExist的值为true,isPartial的值为true,转入步骤5。
步骤5 对表面体素进行二次离散,然后对子体素的每一个体素判断是否被切削。
步骤6 对工件模型中的每个体素依次执行步骤1至5,直至所有体素都完成切削计算,则仿真完成。
本文模型继承了体素模型切削速度快的特点,而且由于其对表面体素进行了进一步的划分和判断,从而在一定程度上提高了仿真的精度。
5 切削面重绘
根据第4节描述,改进体素模型的数据结构的Java描述如图5所示。其中:key为体素的索引值;isExist为体素是否存在的标记;isPartial为体素是否被分割为子体素的标记;subVoxel为存储子体素的三维数组;N为表面体素沿坐标轴方向被分割的次数。
在使用dividing cubes算法进行切削面重绘时,对于未被切削的完整体素,仍需以体素为单位进行绘制,而对于表面体素,则只需要绘制子体素的中心点即可。同时,为了能够提高实体模型的绘制速度,必须在最大程度上避免冗余面(或点)绘制,只对实体模型的外表面和有效切削面进行绘制,不对实体内部的无用面进行绘制。具体绘制算法如下:
步骤1 对于任意体素voxel[i][j][k],根据体素是否存在的标志位isExsit判断该单元体是否存在。若体素存在,则转入步骤2,否则转入步骤5。
步骤2 若该体素存在且不是表面体素,则转入步骤3, 否则转入步骤4。
步骤3 根据式(2)判断该体素是否位于工件离散模型的表面。若是则需要绘制相应面,否则根据该单元体的索引值算出6个与其各个面相邻的体素,voxel[i-1][j][k],voxel[i+1][j][k],voxel[i][j-1][k],voxel[i][j+1][k],voxel[i][j][k-1],voxel[i][j][k+1],依次判断这些体素是否存在。若不存在,则根据需要绘制相应面。例如,如果voxel[i][j][k]存在且不是位于工件离散模型的表面,而voxel[i-1][j][k]不存在,则需要绘制voxel[i][j][k]的左表面;若voxel[i+1][j][k]不存在,则需要绘制voxel[i][j][k]的右表面。同理可对上、下、前、后表面按需绘制。
i=1 显示左表面
i=nx 显示右表面
j=1 显示前表面
j=ny 显示后表面
k=1 显示下表面
k=nz 顯示上表面 (2)
步骤4 若该体素是表面体素,则对子体素运用基于体素模型的切削计算进行判断该体素是否被切削。若该体素未被切削,则求该体素的中心点坐标,并在该坐标位置绘制一个像素大小的点;若该体素已被切削,则无需对该体素进行绘制。
步骤5 依次执行步骤1至4,直至所有体素绘制完成。
图6为在初始状态下,利用本文体素模型对工件进行建模的效果图。
6 实验结果
实验中如果一级离散精度过高,则会产生大量离散数据,不仅会占用大量的内存空间,而且会降低切削效率;相反,如果一级离散精度过低,则大部分体素会被部分切削,成为表面体素,从而产生大量的二级离散数据,同样会浪费大量内存空间、降低切削效率。综合这两点考虑,将一级离散精度设置为R2个单位长度。本文实验的硬件环境为:Windows10操作系统,17-2640M双核CPU,16 G内存。实验中,刀具半径为5个单位长度,毛坯的长、宽、高分别为120、120和30个单位长度。
图7展示了在相同实验环境下,基于体素模型和marching cubes算法的切削时间和本文算法在二级离散精度分别为2×2×2,4×4×4和5×5×5时切削时间的对比图。
从图7可以看出:以每1 000个刀位点的切削时间对比,基于dividing cubes算法思想的切削计算有较高的切削效率,但随着二级离散精度的提高,切削效率随之下降。
7 结语
本文根据dividing cubes算法的思想,对体素模型进行了改进,并在此基础上提出了对应的切削算法。实验证明该算法可以在保证切削精度的同时,有更高的切削效率,并且基于dividing cubes算法的切削面的重绘过程也更加简洁。但是该算法会受到二级离散精度的影响,随着二级离散精度的提高,切削计算量会增加,切削效率会下降,同时也需要更多的计算机内存。因此,在实际应用中需要根据实际情况选择合适的二级离散精度。
参考文献:
[1]REQUICHA A A G, VOELCKER H B. Solid modeling: current status and research directions[J]. IEEE Computer Graphics and Applications, 1983, 3(7): 25-37.
[2]闫立华. 数控仿真系统的几何建模方法研究与设计[D]. 秦皇岛: 燕山大学, 2006.
[3]JANG D G, KIM K, JUNG J M. Voxel-based virtual multi-axis machining[J]. Advanced Manufacturing Technology, 2000, 16(10): 709-713.
[4]VAN HOOK T. Real-time shaded NC milling display[J]. ACM SIGGRAPH Computer Graphics (Comput Graph), 1986, 20(4): 15-20.
[5]候增选, KRAUSE F L, 田荣鑫. 基于压缩Voxel模型的五坐标数控加工仿真新方法[J]. 计算机工程与应用, 2006, 42(20): 25-28.
[6]毛一砚. 五轴数控工具磨床磨削仿真算法研究[D]. 成都: 西南交通大学, 2019.
[7]杨挺, 吴宝海, 李山, 等. 利用密切平面的自由曲面求交算法[J]. 机械科学与技术, 2009, 28(3): 371-374.
[8]张接信, 吴坚. 工程机械零件离散复杂曲面求交算法[J]. 长安大学学报(自然科学版), 2007, 27(5): 116-119.
[9]张少丽, 王毅刚, 陈小雕. 基于空间分解的三角网格模型求交方法[J]. 计算机应用, 2009, 29(10): 2671-2673.
[10]LORENSEN W E, CLINE H E.Marching cubes: a high resolution 3D surface construction algorithm[J]. Computer Graphics, 1987, 21(4): 163-169.
[11]吴建伟, 王子牛. 基于改进 MC 和 MT 算法的CT图像三维重建[J]. 贵州大学学报(自然科学版), 2015, 32(2): 82-85, 93.
[12]CLINE H E, LORENSEN W E, LUDKE S,et al. Two algorithms for the three-dimensional reconstruction of tomograms[J]. Medical Physics, 1988, 15(3): 29-37.
[13]王哲, 王知行, 钟诗胜. 刀具扫描体生成新算法及在数控加工仿真中的应用[J]. 机械工程学报, 2001, 37(1): 28-31.
[14]李杨, 王子牛, 王彦, 等. 基于刀具空间包围体算法的数控切削仿真[J]. 计算机工程与设计, 2012, 33(3): 1073-1078.
(责任编辑:周晓南)
Abstract:
Cutting calculation is an important part of the CNC simulation system. Different cutting algorithms directly affect cutting efficiency and cutting accuracy. Based on the idea of dividing cubes algorithm, a new cutting algorithm is proposed by slightly changing the voxel model. The experiment results shows that this method can ensure the cutting accuracy and has higher cutting efficiency, and the redrawing process of cutting surface based on dividing cubes algorithm is more concise and efficient. However, this method requires different memory space according to the discrete accuracy of the rough. At the same time, it is found that when the discrete accuracy of the rough exceeds a certain degree, the amount of cutting calculation will be increased, and the efficiency of cutting calculation will be reduced.
Key words:
CNC simulation; voxel model; dividing cubes; cutting calculation

