考虑紧急备用与光伏出力不确定性的微电网分布式储能规划方法

吴彬锋，傅 颖，陈扬哲，刘子卓，江道灼，朱乃璇，徐伟丰

（1.国网浙江省电力有限公司丽水供电公司，浙江 丽水 323000；2.国网浙江松阳县供电有限公司，浙江 丽水 323400；3.浙江大学 电气工程学院，杭州 310027）

0 引言

面临日益严重的环境污染问题，降低碳排放已成为人类社会的广泛共识。中国政府提出了2030 年前实现“碳达峰”、2060 年前实现“碳中和”的目标[1]。大规模的可再生能源建设一方面为降低碳排放做出贡献，另一方面也为电力系统带来了不确定性和波动性的挑战。为解决分布式可再生能源固有的间歇性、随机性等问题和应对相关的电力电子装置带来的控制复杂度、系统稳定性等风险，建设微电网以消纳分布式可再生能源并实现优化调度成为一种可行的解决手段[2-4]。

微电网的优化配置关系到微电网的经济效益、运行功能等，是微电网建设中的重要课题[5]。微电网内的分布式电池储能系统作为低惯量系统，具备快速充放电响应的能力，从而平抑系统中的功率波动和为系统提供紧急备用电源，同时能通过降低线路损耗、“低充高放”套利等方式提高系统的经济性[6-7]。

储能系统的选址定容问题是微电网的优化配置重要组成部分。文献[8-9]以配电网中分布式储能系统的选址定容规划为研究对象，以提高配电网整体的运行效益，但其采用了直流潮流法或PQ 分解法，未充分考虑储能自身的功率数学特性与系统潮流方程特征的结合；文献[10]建立了结合储能健康状态、寿命损耗和效率的综合动态模型，依此建立光储充电站的混合整数非线性双层规划模型并采用遗传算法求解；文献[11]分析了采用储能替代发输配电设备与无功补偿装置的收益，并采用变异粒子群算法求解储能配置双层优化问题；文献[12]提出了改进鲸鱼算法求解储能系统的优化配置模型。上述文献采用的启发式算法虽克服了局部最优或优化速度问题，但却降低了优化结果的可解释性。文献[13]综合考虑储能的配置成本和运行化效果，研究了混合型储能的容量配置问题并以粒子群算法求解，但研究者主要配置储能的类型和容量，未考虑其接入位置的选址问题。微电网中的储能系统通过其灵活充放电策略，平抑系统中可再生能源出力的随机性和用户负荷的波动性[14]。为有效衡量系统的不确定性，国内外学者开展了大量研究。文献[15]基于历史数据，以蒙特卡洛方法模拟系统中光伏典型的接入场景，并在基础上优化光伏的装机容量。文献[16]采用条件风险价值衡量源-荷不确定性对系统调度者的决策影响，基于风险偏好得出优化调度策略。以上方法可以有效评估系统内的不确定性因素，但易忽视极端场景。而鲁棒优化作为涵盖极端场景的随机规划方法，被广泛应用于电力系统的不确定性研究中[17-18]，以使系统的规划配置得以在最恶劣的不确定性场景下提供优化的调度策略。文献[19]针对主动配电网内分布式电源的不确定性问题，分解为配电网侧和可控资源侧的分布式优化子问题，建立并求解了主动配电网的鲁棒优化调度模型。

为此，在考虑系统紧急备用和可再生能源出力不确定性的条件下，本文以分布式光伏为例，推导了结合网络潮流特征的储能出力二阶锥规划模型，并采用鲁棒模型描述光伏出力不确定性，建立微电网中分布式储能系统选址定容的两阶段混合整数二阶锥规划问题，提出一种结合列与约束生成算法、大M 法的求解算法，以修改后的IEEE 22 节点为例验证了本文算法的正确性和有效性。

1 微电网数学建模

1.1 光伏出力不确定性模型

随着可再生能源渗透率的提高，分布式光伏阵列和分布式风力发电成为微电网内不确定性的主要来源，而本文着重考虑分布式光伏给微电网带来的出力不确定性。当光伏阵列的安装容量固定时，若采用最大功率点跟踪的控制策略，其实际出力受到光照强度、环境温度等环境条件影响。在一年期的优化问题中，将相似的外部环境条件聚类为若干个典型光伏运行场景，并采用预测有功出力序列表征各场景中分布式光伏的分时输出功率，并引入预测误差以表征光伏实时出力相较于预测值的不确定性，即：

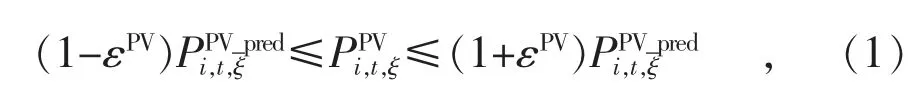
1.2 发电机模型

通过配置微型发电机作为微电网的主电源，使得微电网需具备一定的孤岛运行能力。微型发电机的出力范围受其安装容量约束，通常表示为：

1.3 支路潮流模型

类似传统的中低压交流配电网，本文考虑微电网的结构为辐射状网络，如图1 所示，可采用BFM（支路潮流模型）作为微电网的潮流计算公式[20]，即：

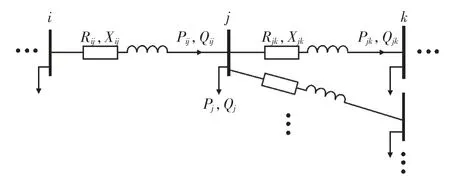
图1 辐射状微电网潮流模型

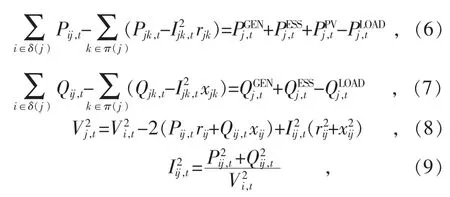
式中：δ（j）为节点j 父节点的集合；π（j）为节点j子节点的集合；Pij，t，Qij，t和Iij，t分别为从节点i 流向j 的有功功率、无功功率和电流；Vi，t为节点i在t 时刻的电压；rij和xij为线路ij 的电阻和电抗；为场景ξ 中节点j 在t 时刻的有功和无功负荷；为节点j 安装储能系统在t 时刻输出的有功和无功功率。

为了将上述潮流计算模型表示为可采用SOCP（二阶锥规划）算法求解的数学模式，作如下等量替换：

此外，将式（9）进行二阶锥松弛，结合上述等量替换，得到符合SOCP 形式的潮流计算公式如下[21]：

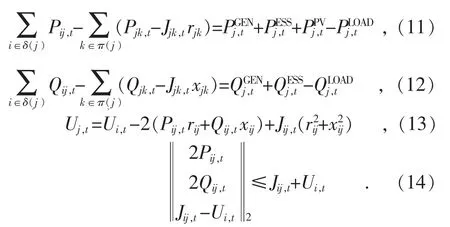
1.4 四象限储能系统模型

将储能电池与双向换流器连接，施加适当的控制策略，可实现储能系统的四象限运行[22]，其拓扑结构如图2 所示。

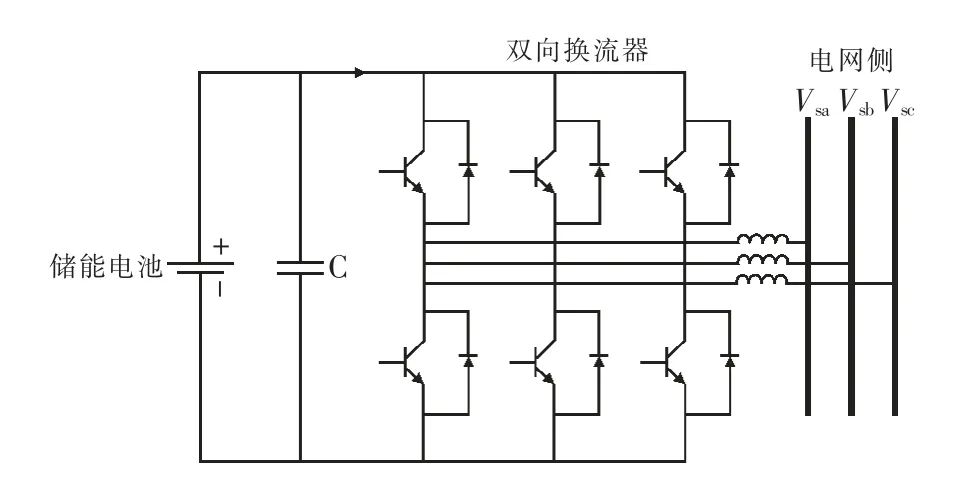
图2 四象限运行分布式储能系统拓扑结构

储能系统的运行功率受该双向换流器的容量约束，即：

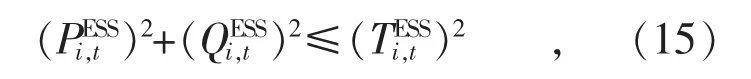
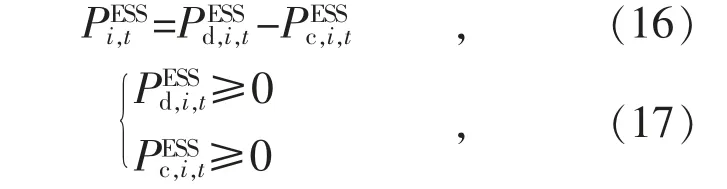
根据上述对储能系统有功无功功率的定义与分解，式（15）可以转换为二阶锥形式：

通过该二阶锥模型的转化，与系统二阶锥潮流模型结合，避免了充放标志电0-1 变量和功率容量线性化0-1 变量的引入，使得系统优化建模更具统一性。

储能系统的另一关键参数为储能电池SOC（荷电状态），与储能的充放电功率相关，即：

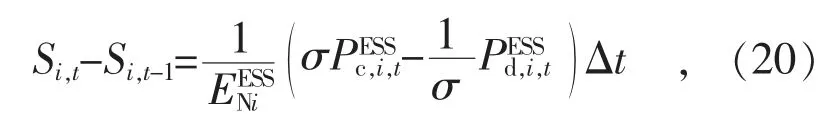
式中：Si，t为节点i 在t 时刻的SOC；σ∈（0，1）为储能电池的充放电效率；为储能电池的额定电量；Δt 为调度的单位时间，通常为1 h。

在调度周期T 完成后，储能的SOC 需保持与初始SOC 相等以实现可持续的运行：

考虑到储能电池的使用寿命，其放电深度需要加以限制，即储能SOC 需满足：

1.5 紧急备用约束建模

为应对发电机脱网、线路损坏等严重系统故障，设置储能系统作为系统的紧急备用，并以储能SOC 量度系统紧急备用的大小。当严重故障发生时，一定比例的重要负荷需保障其供电，因此用式（26）表示系统紧急备用：

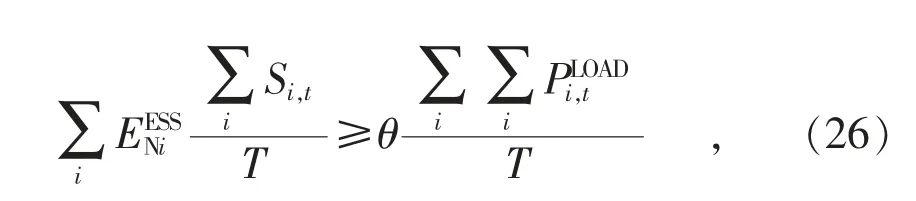
式中：θ 为微电网系统中重要负荷的比例。

2 两阶段鲁棒优化模型

2.1 目标函数

本文研究的主要问题是：在面临光伏出力不确定性的挑战下，微电网中分布式储能系统如何进行选址定容且为系统提供紧急备用，并给出微电网系统的优化调度策略。因此，本文优化问题的成本函数由储能投资维护成本FESS、储能运行损耗成本、系统发电成本FGEN和线路损耗成本构成，即：

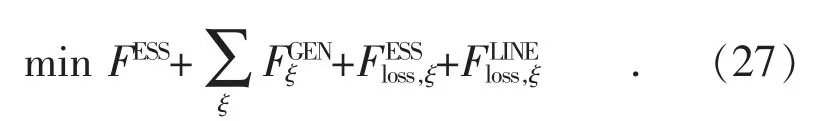
2.1.1 储能投资维护成本

通常而言，储能的投资成本为一次性投入、多年使用，维护成本则按年计。因此需要将投资成本折算为单年成本，并将单年投资成本与维护成本结合后折算至研究问题的单日成本。其中，投资成本与储能电池电量和换流器容量相关，维护成本与换流器容量相关。

2.1.2 发电成本

本文采用发电成本正比于微型发电机有功出力的模型，且单位出力价格随时间变动，类似电价机制，故场景ξ 下的发电成本为：

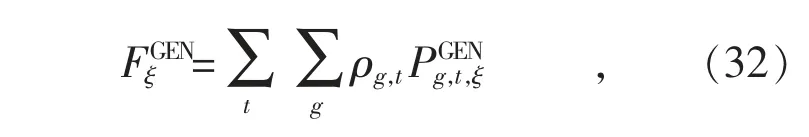
式中：ρg，t为微型发电机g 在t 时刻的单位出力价格。

2.1.3 线路损耗成本

由于微型发电机的单位出力价格随时间变化，而线路上的功率损耗可视作发电机出力的抵消，因此单位线路损耗成本同样随时间变化，故场景ξ 下的线路损耗成本为：

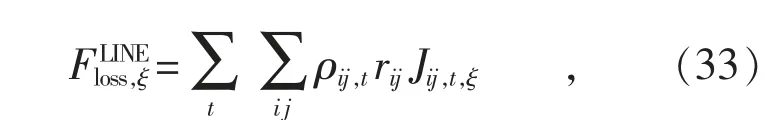
式 中：ρij，t为线路ij 在t 时刻的单位线路损耗成本；rij为线路ij 的电阻值；Jij，t，ξ为式（10）所示场景ξ 下t 时刻从节点i 流向j 的电流的平方值。

2.1.4 储能运行损耗成本

通过双向换流器实现四象限运行的储能系统，它在调度周期内的运行损耗可使用其充放电功率衡量，并认为单位损耗成本亦与时间相关，即：

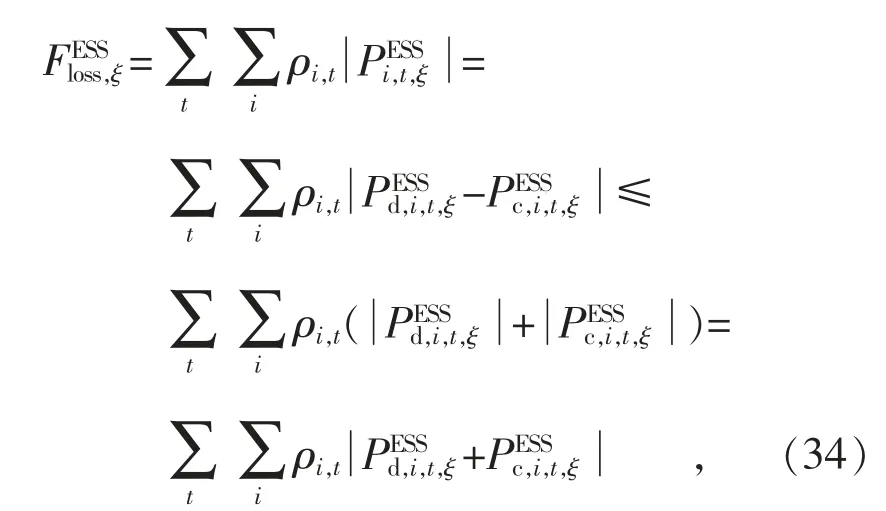
式中：ρi，t为储能i 在t 时刻的单位运行损耗成本。基于前文对储能充放电功率的约束，可采用绝对值不等式将储能运行成本表示为线性化函数。

2.2 两阶段鲁棒问题建模

从储能系统的数学模型可以看出，微电网系统的运行调度策略受到分布式储能选址定容结果的约束，同时，给出的调度策略需应对光伏的出力波动性带来实际可能的最差运行工况。故本文的优化问题是典型的两阶段鲁棒优化问题，可表示为如下形式：

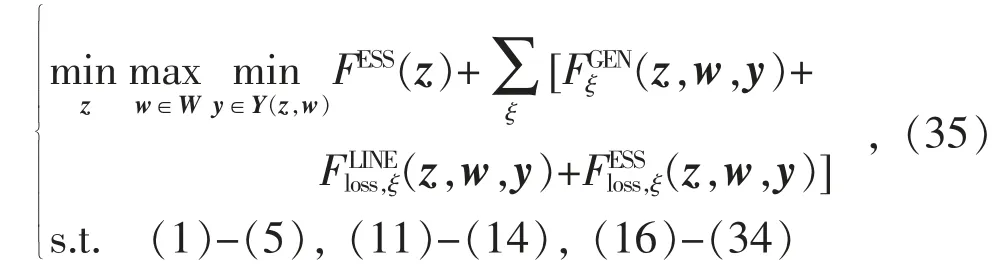
式中：z 为第一阶段的分布式储能选址定容变量；y 为第二阶段的系统运行状态变量；w 为具有不确定性的光伏出力变量；W 为式（1）表示的光伏出力范围。

该优化问题由第一阶段的min 问题和第二阶段的max-min 问题组成，其中第一阶段问题关注的是储能选址定容的规划成本最小化，第二阶段引入鲁棒优化，以max 问题表示“最恶劣”的光伏实际出力工况，而min 问题则为在该“最恶劣”工况下尽可能最小化由发电成本、线路损耗成本和储能运行损耗成本组成的实时运行成本。

以紧凑矩阵形式表示该两阶段优化问题，即：

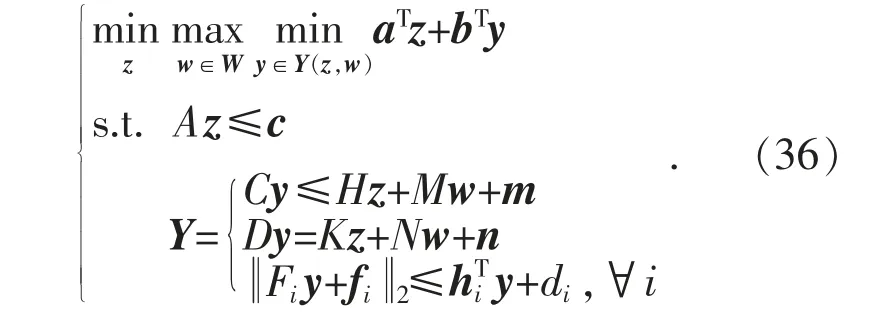
3 求解算法

3.1 C&CG 算法

针对式（36）表示的两阶段鲁棒优化问题，本文使用列与C&CG（约束生成算法）进行求解。C&CG算法将原始的两阶段问题分解为主问题和子问题，通过两者交替求解得到原始问题的最优解。在每次迭代求解主问题时，C&CG 算法会根据子问题的求解情况，为主问题生成与子问题相关的变量和约束，虽然可能导致每次迭代求解主问题的时长更长，但能有效降低问题的迭代次数[23]。

分解式（36）得到对应的MP（主问题）如下：

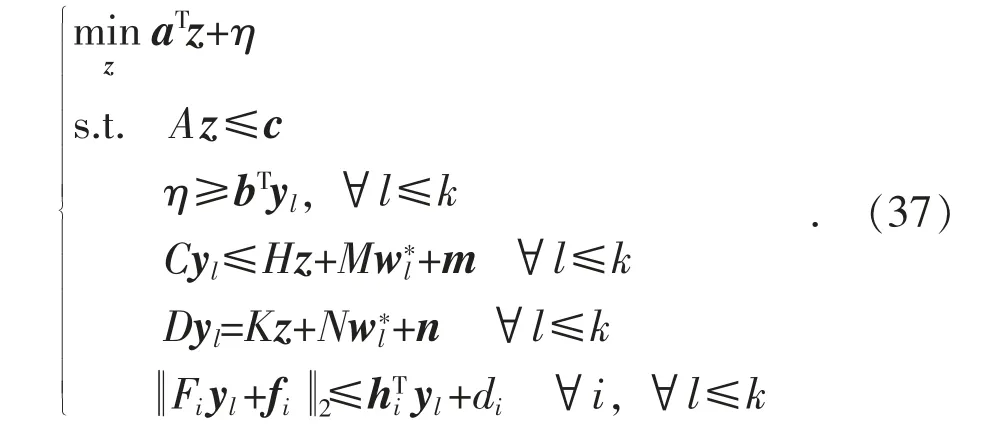
分解式（36）得到对应的SP（子问题）如下：

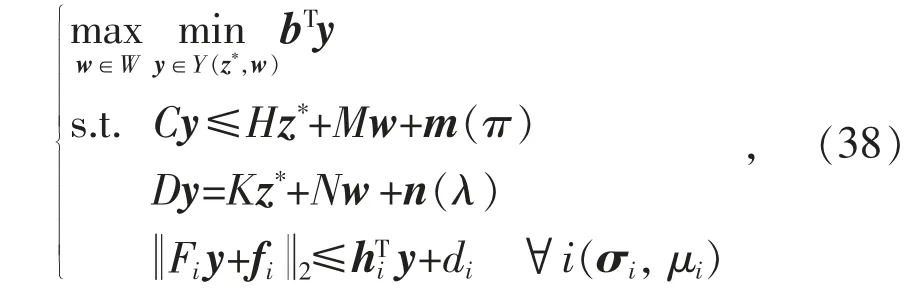
式中：各括号中π，λ，σi和μi为对应约束的对偶乘子。

3.2 子问题转换：强对偶原理

式（38）表示的子问题有线性的目标函数和二阶锥形式的约束，具有二阶锥规划的特征。根据强对偶原理，将子问题目标函数的内层min 问题转换为对应的对偶max 问题，从而合并得到具有max 形式目标函数的子问题如下：

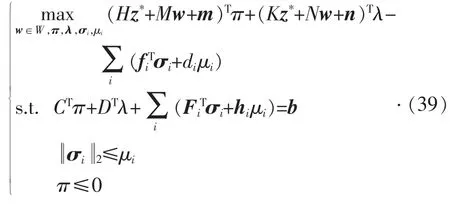
3.3 双线性项转换：大M 法

对偶变形之后，式（39）的目标函数包含了（Mw）Tπ 和（Nw）Tλ 这类的双线性项，不满足凸优化的条件，无法直接求解，故采用大M 法将其转换为可求解的形式。

不确定性变量w 所属的集合W 为区间集合，根据优化理论，目标函数的最优值在区间端点处取得。定义0-1 变量δs表征w 取得区间的最大值或最小值，即：

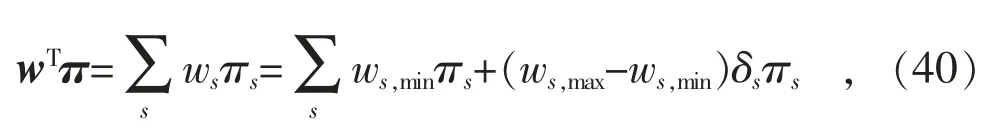
其中，当δs=0 时，ws取得其最小值ws，min；当δs=1时，ws取得其最大值ws，max。进一步，定义连续变量γs=δsπs，用大M 法转换式（40），得到：

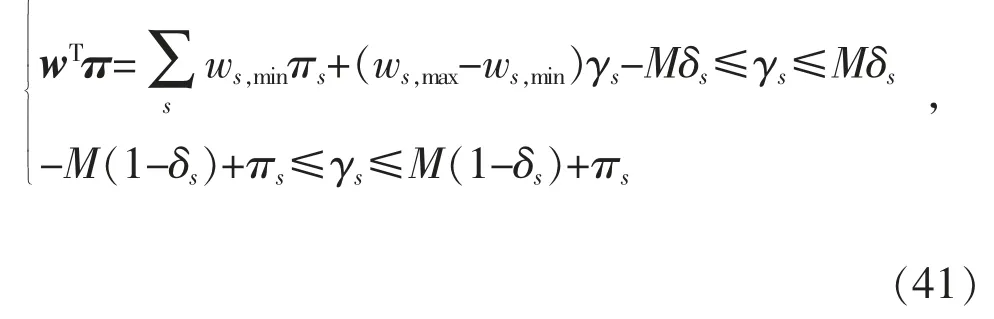
式中：M 为足够大的正整数。

最后，将式（41）代入对偶合并后的优化子问题（39），得到混合整数二阶锥规划形式的子问题，记为Dual-SP。

3.4 C&CG 算法求解流程

基于以上变形，C&CG 算法的求解流程如下：

第1 步：初始化收敛下界LB=-∞，收敛上界UB=+∞，迭代次数k=1，输入算法的收敛误差ε。

第2 步：对于给定不确定性变量的取值w*，调用MISOCP 求解器求解主问题MP，得到一组最优解（z*，η*，yl*），l=1，2，…，k，并更新下界LB=min{LB，aTz*+η*}。

第3 步：根据第2 步求解MP 得到的z*，代入求解MISOCP 子问题Dual-SP。

（1）若子问题可解，则得到最优解（w*，π*，λ*，，）和对应的最优目标函数值θ（z*）。

（2）若子问题无解，则θ（z*）=+∞，进而更新上界如下：UB=max{UB，aTz*+θ（z*）}。

第4 步：若UB-LB≤ε，则返回最优解与对应的目标函数值，否则：

（1）若子问题可解，则生成新变量yl+1，并添加下列约束至主问题MP：

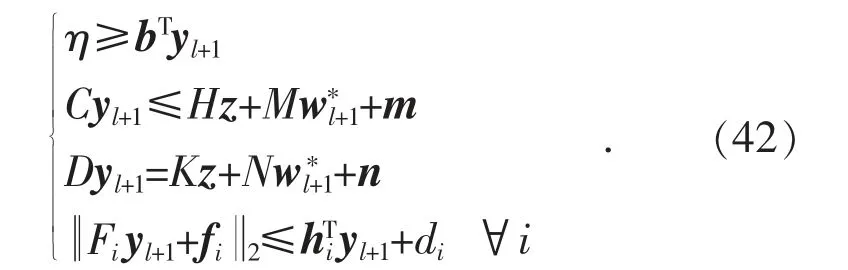
（2）若子问题无解，则生成新变量yl+1，并添加下列约束至主问题MP：

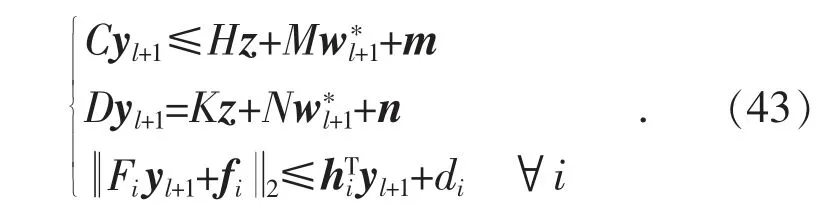
第5 步：令迭代次数k=k+1，返回第2 步。

4 算例分析

4.1 算例信息

本文以修改后IEEE 22 节点辐射状电网[24]作为微电网算例进行优化仿真验证，在节点16 处安装容量为4.5 MW 的分布式光伏电站，如图3所示。随时间变化的单位功率成本列举于表1中，表2 为仿真算例的其他关键参数。

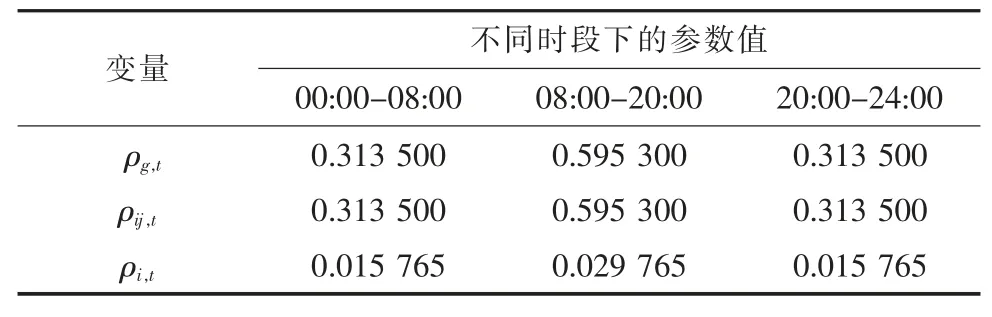
表1 随时间变化的单位功率成本参数

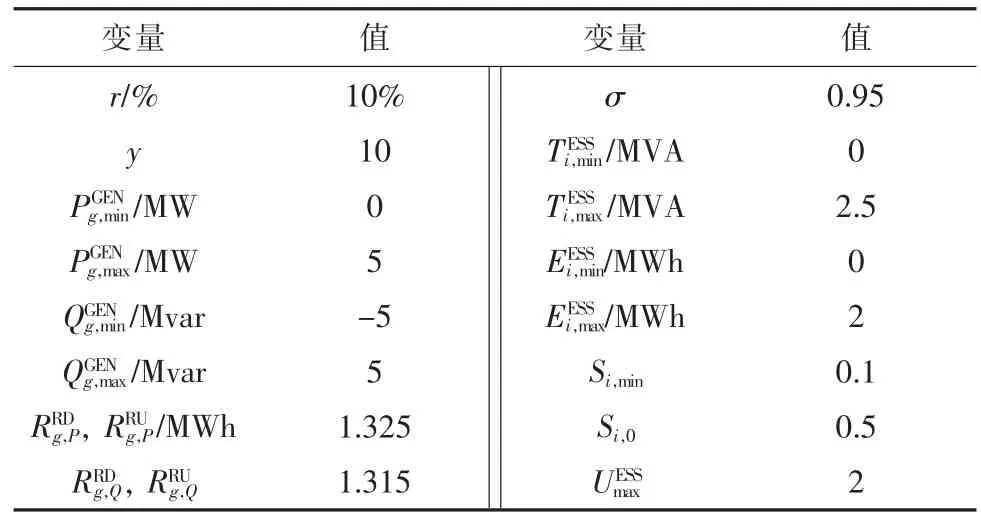
表2 仿真算例的关键参数

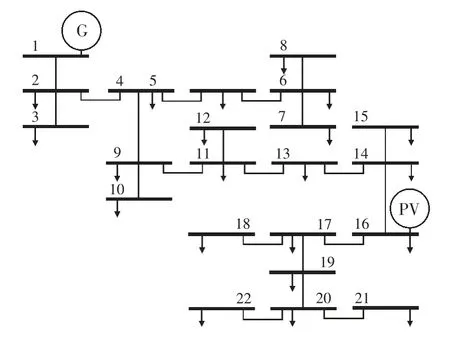
图3 修改后的IEEE 22 微电网系统仿真算例

本文考虑春夏运行场景和秋冬运行场景这2个典型运行场景以表征微电网系统调度在一年内的运行特征。这些运行场景内的光伏预测出力、负荷曲线以标幺值形式如图4 所示。

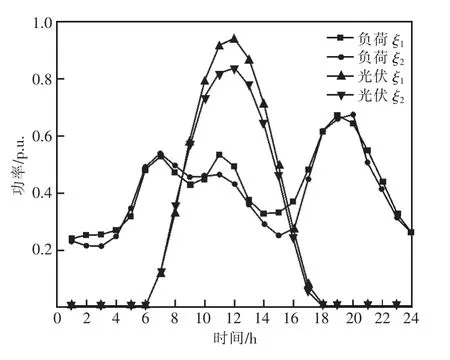
图4 春夏、秋冬典型运行场景光伏与负荷曲线

4.2 微电网优化运行结果

根据上述参数，在MATLAB 软件中编程C&CG 算法，调用CPLEX 求解器求解第二、三章所述的两阶段鲁棒优化模型。

在表2 给出的微电网内安装的分布式储能套数、容量、储能电池电量的上限及其他关键约束下，经迭代求解以后，得到的分布式储能系统选址定容结果及投资维护成本如表3 所示，在不同场景下的系统运行成本如表4 所示。

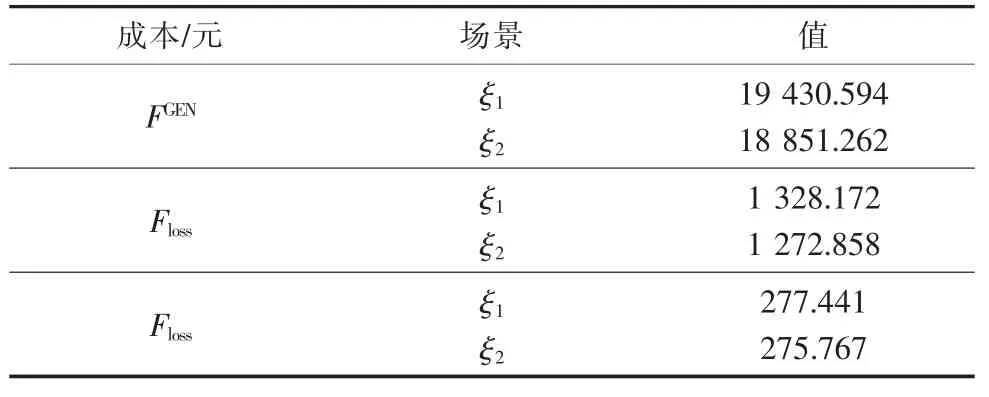
表4 第二阶段各项运行调度成本优化结果

分析表3 得出的选址结果，微电网中共安装了两套分布式储能系统，即为约束的套数上限。储能系统的一号选址点节点16 为光伏接入点，微电网系统中，光伏的出力具有较大波动性，配置储能系统可以平抑系统的波动从而平稳运行，相较配置储能前降低了节点16 处约8.5%的功率波动；储能系统的二号选址点节点20 靠近微电网网络末端，由于储能系统具有四象限运行能力，安装于末端的储能系统可以为系统提供无功支撑，稳定系统末端节点的电压水平。

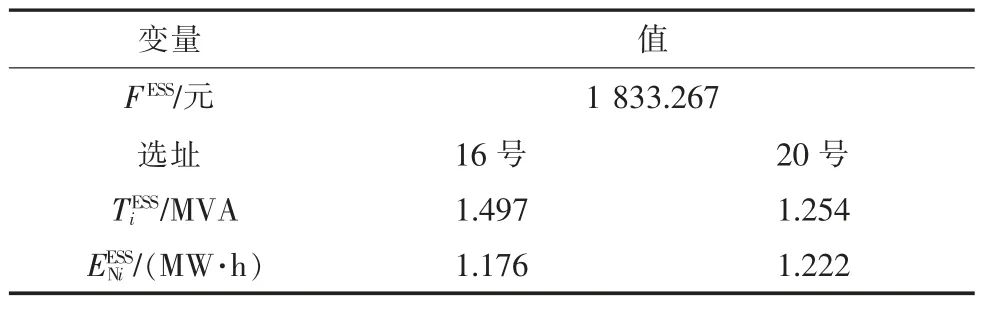
表3 第一阶段储能选址定容及成本优化结果

不同典型场景下微电网系统的优化调度策略如图5 所示。

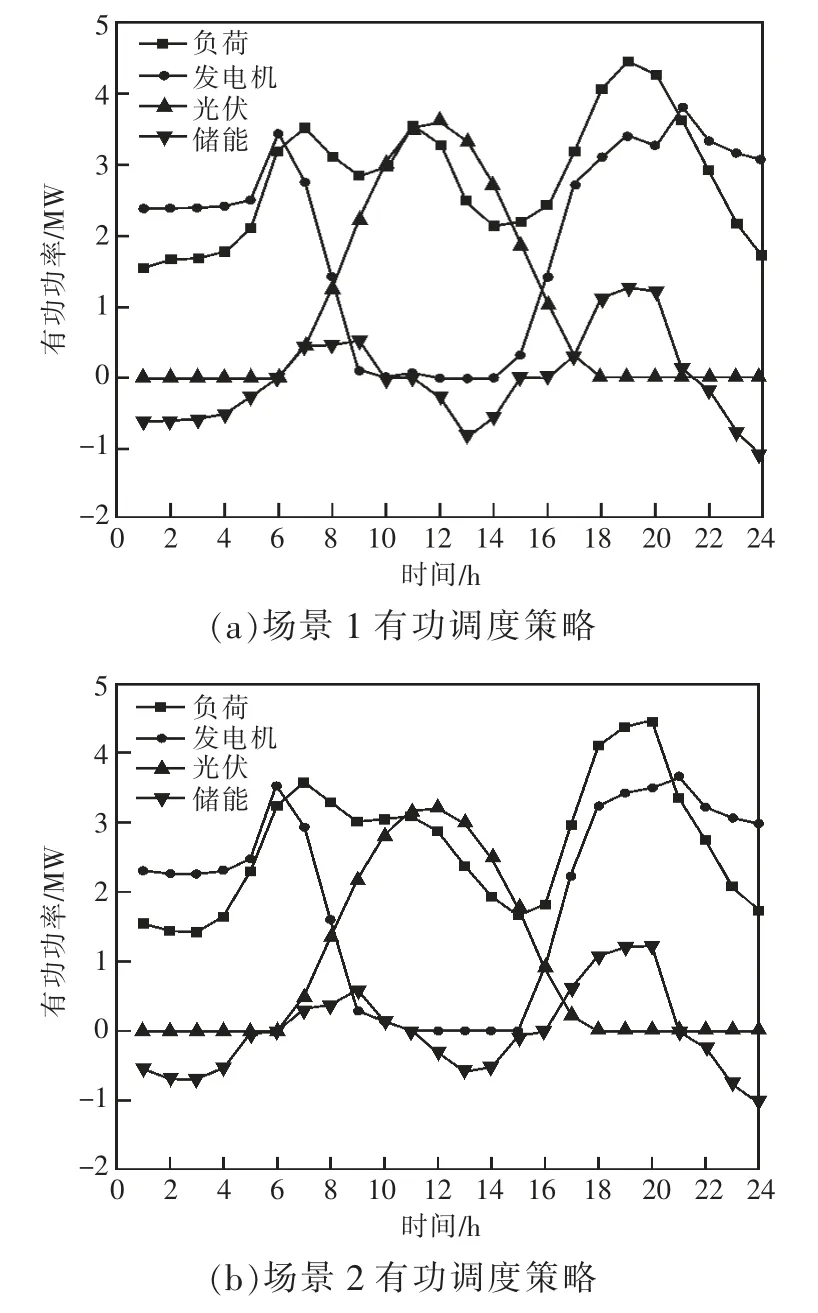
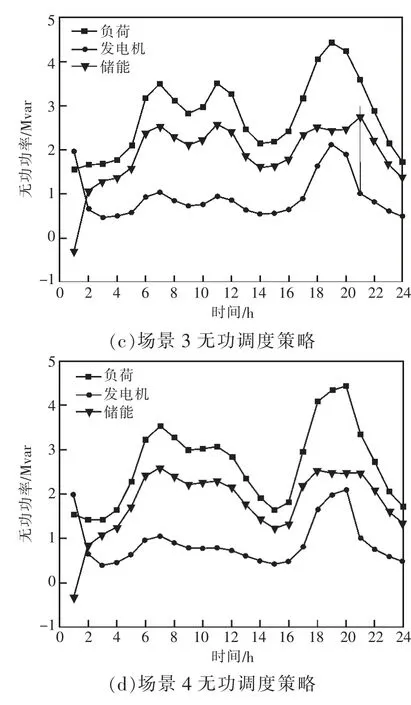
图5 不同典型场景下微电网系统的优化调度策略

针对图5 所示的春夏、秋冬两类典型场景微电网系统的优化调度策略进行分析，有如下结论：当光伏出力抬升时，发电成本较高的微型发电机出力逐渐下降，系统负荷由储能系统和光伏出力共同支撑；微电网配置的储能系统均倾向于在低电价时段充电，高电价时段放电，相较配置储能前，降低发电成本约5%，降低线损成本约15%；为应对光伏或负荷的快速波动，储能需进行大量有功充放电操作，此时储能的无功功率变动平缓，以满足储能的容量约束。

5 结论

分布式储能系统可以平抑可再生能源出力的波动并为微电网提供运行辅助。本文针对微电网中分布式光伏的出力不确定性，围绕微电网建设中关键的分布式储能系统规划配置问题，主要有如下贡献：

建立了结合系统支路潮流模型与储能四象限运行特点的二阶锥规划潮流模型，该模型对每组储能设备减少了2 个充放电标志0-1 变量和2 组以上的功率容量线性化0-1 变量，提高优化建模统一性。

提出了以鲁棒优化方法寻找光伏出力波动的最差运行工况，从而建立应对不确定性结合系统紧急备用约束下的微电网储能系统选址定容的方法并基于算例求解结论，验证了分布式储能系统在光伏接入点降低了约8.5%的功率波动，并降低系统发电成本约5%，降低网络线损成本约15%。

作为本文工作的补充，后续工作应着重于研究考虑分布式光伏和风电联合优化建模的问题，并深入剖析优化算法，以求提高算法求解速度和效率。