储能参与一次调频的优化控制策略研究

马骏超，周洁洁，江全元，丁 可，倪秋龙，石博隆

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.国网浙江省电力有限公司杭州供电公司，杭州 310009；3.浙江大学 电气工程学院，杭州 310027；4.国网浙江省电力有限公司，杭州 310007）

0 引言

受碳达峰和碳中和的“双碳目标”影响，传统火电机组发展受限，新能源并网渗透率不断提高[1]，电网调频压力激增，对于电网频率的安全稳定控制近年来受到广泛关注。

浙江电网是典型的受端电网，受到能源“双控”政策影响，特高压直流外送电的大规模接入和新能源渗透率的不断提高，电力系统的稳定运行特别是频率稳定方面带来了巨大的挑战。新能源渗透率的增加不仅会增加系统的不确定性，还会降低电网的惯性，使频率在电力扰动下更容易发生变化[2-3]。此外，随着社会用电量的增加以及电动汽车等新型负荷的接入，用电负荷的波动性也随之上升。而传统调频机组具有响应速度慢、爬坡速度受限、调频能力不足等缺点，已经愈发难以满足浙江电网调频需求，进一步加剧了频率稳定问题。

电化学储能具有响应快、充放电灵活等优点，在调频方面得到了广泛的应用[4-8]。目前，国内外已有一大批商用的电化学储能系统应用于电网频率控制。美国PJM 市场用于频率调节的储能装机容量已超过200 MW，国内在石景山热电厂首个储能参与调频商业示范工程实施后，山西电网也相继实施了多个类似工程。

目前，储能参与一次调频主要是基于量测信息的控制策略。文献[9]提出一种基于比例控制的储能调频控制策略，使储能系统模拟常规机组的一次调频响应。文献[10]所提出的控制策略综合了微分控制和比例控制（PD 控制）的特点，使储能系统模拟常规机组的惯性响应和一次调频响应。文献[11]提出一种基于模糊逻辑控制的储能快速调频策略，输入系统频率偏差大小及其变化率，然后根据所设计的模糊逻辑策略，输出储能参与快速调频的有功功率。文献[12]提出了一种基于功率-频率特性曲线的储能参与快速调频控制方法，当系统频率发生变化时，根据所设计的功率-频率特性曲线，动态调整储能参与快速调频的有功功率。然而，上述研究中所使用的控制参数，需要运行人员根据工程经验提前确定。因此，所设定的参数对于复杂实际系统工况不一定具有适应性。针对上述问题，本文研究基于下垂控制方式的储能一次调频参数优化方法。目前，关于储能一次调频下垂控制的研究主要集中在储能功率和容量的优化[13-15]。而在应对复杂实际工况时，储能的调差系数和调频死区的优化选取更为重要，不合理的取值会影响电力系统的稳定性和储能的经济性。

为此，本文基于浙江电网搭建了统一频率数值仿真模型，分析浙江电网对储能参与一次调频的需求及应用效果，在此基础上提出储能调频参数的优化选取方法，旨在提升储能的功能性和经济性。

1 储能参与一次调频优化控制

本节首先根据浙江电网数据建立统一频率模型，在统一频率模型的基础上建立储能参与一次调频参数优化模型，基于新能源和负荷的预测数据对参数进行动态优化。

1.1 统一频率模型

1.1.1 统一频率模型介绍

目前，国内华东地区电力调度机构和科研院所主要基于BPA 软件开展电力系统仿真分析工作，软件已被国内运行、生产、规划、科研以及大学等单位广泛应用。

但是，在BPA 关于频率的仿真计算中，首先需要对系统进行潮流计算，再基于潮流计算的结果，获取系统稳态运行点，进行暂态计算。用来表征频率的参数是各台机组的转速，基于此利用加权平均的方式获得整个系统的频率。在这种计算方式下，程序运行速度缓慢。另外，由于BPA的局限性，无法自主增加新的模型和模块。

针对此问题，本文基于浙江电网和机电网潮流组数据，搭建了统一频率模型[16]，所提出的浙江电网统一频率模型框架如图1 所示。其中Meq为系统惯性，由系统全机组惯性特性决定，Deq为省内负荷调节系数。另外，新能源并网功率包括风电功率和光伏功率，新能源并网功率和直流外受电作为本文主要功率扰动输入。

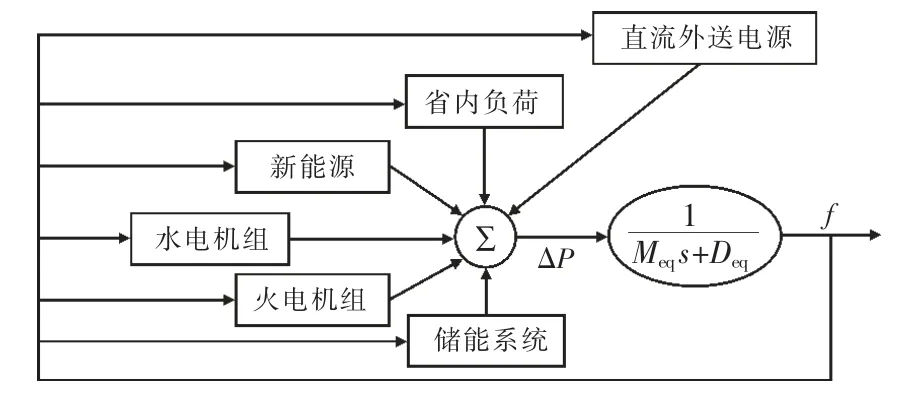
图1 统一频率模型框架

当系统中有新能源以及储能接入时，系统固有频率特性可用式（1）表示：

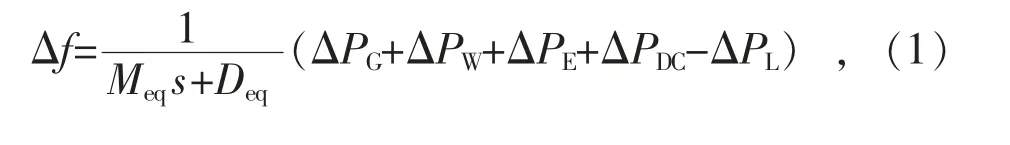
式中：ΔPG为常规机组总出力变化；ΔPW为新能源出力变化；ΔPE为储能出力变化；ΔPDC为直流外送的功率变化；ΔPL为系统负荷变化。

对式（1）进行差分化，可得电力系统频率的递推表达式如式（2）所示：

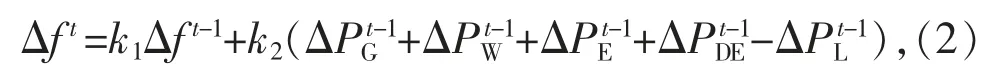
式中：k1，k2分别为系统等效旋转惯量和负荷频率调节效应系数相关的系数，可由式（3）求得：

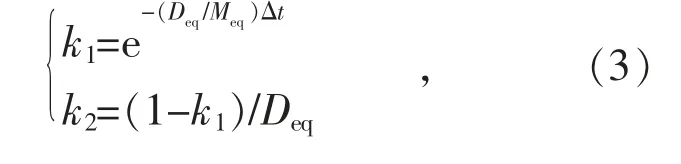
式中：Δt 为差分化的时间步长。

浙江电网有火电机组和水电机组，火电机组为GA-GJ-TB 型，分别由GA型电液伺服机构、GJ 型调节系统模型和TB 型汽轮机组接而成；水电机组为GH 型。文献[17]研究了搭建统一频率模型的方法，可以结合PSD-BPA 稳定说明书的结构图建立浙江电网统一频率模型。

1.1.2 储能频率控制模型

当系统出现故障或扰动时，频率会响应变化。储能系统根据系统频率偏差，采用下垂控制模式动态调整有功出力，其控制模型主要包括了死区环节、下垂环节两部分，如图2 所示。

图2 储能辅助调频控制方式

当频率偏差在死区范围内时，储能系统既不充电也不放电，此时对应的有功指令为零；当频率偏差超过正向死区时，储能系统从电网吸收功率，并根据下垂系数动态调整其有功指令大小；当频率偏差超过负向死区时，储能系统向电网释放功率，也根据下垂系数动态调整其有功指令大小，如式（4）所示：

1.2 参数优化

1.2.1 控制流程

根据上节建立的统一频率模型，本文的优化控制策略是一种基于新能源和负荷超短期预测的动态优化方法，如图3 所示。在当前时段，基于可再生能源和负荷超短期预测结果，优化下一时段储能控制器参数，并在对应时段到来时将对应参数投入运行。

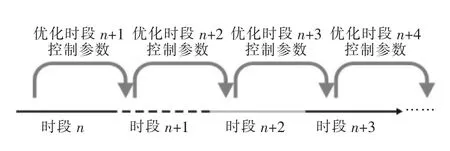
图3 动态优化示意

实现动态优化的基础是功率超短期预测和优化过程的计算时间。功率预测的准确性对优化结果有十分重要的影响。目前，功率超短期预测的准确性已经达到了较高水平，因此，本文不考虑功率预测精度对优化过程的影响。

其中优化模型中的目标函数的权重因子由该优化时段的预测数据确定，以此兼顾储能的调频能力和经济性。

1.2.2 目标函数和模型约束

选取储能频率调节死区fd以及频率调差率%作为储能一次调频控制的待优化变量。当频率出现偏移时，如果储能一次调频的死区或调差率过大，则会无法及时动作，反之如果死区或调差率过小，储能则可能会进行过多不必要的动作，从而影响储能寿命。

本方法是基于新能源和负荷的短期预测数据来进行动态优化，所需的预测数据如式（5）—（8）所示：

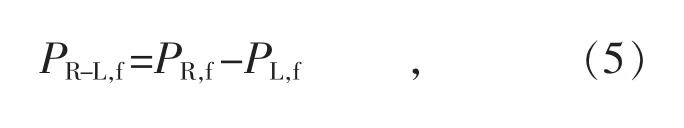
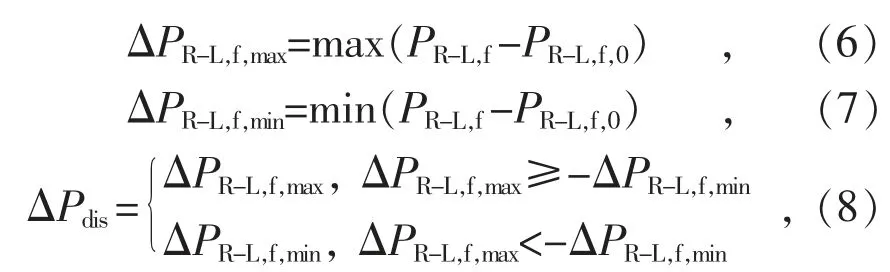
式中：PR，f为短期预测的可再生能源有功功率；PL，f为短期预测的负荷有功功率；PR-L，f为短期预测的可再生能源功率与负荷功率之差；PR-L，f，0为待优化时段初始时刻的PR-L，f；ΔPR-L，f，max为ΔPR-L，f与PR-L，f，0功率之差的最大值；ΔPR-L，f，min为ΔPR-L，f与PR-L，f，0功率之差的最小值。

为了平衡系统频率偏差和储能经济性的关系，本文在目标函数中同时考虑频率偏差及储能使用量，即：

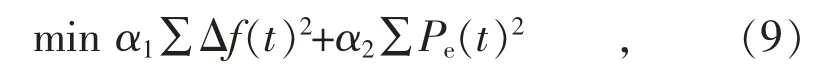
式中：Δf 为系统频率偏移量；Pe为储能的出力；α1和α2为目标函数的权重因子，并满足以下条件：

如果α1较大，意味着优化的结果希望减小频率偏差，为了达到这个目的，允许储能适当较多的动作；如果α2较大，意味着优化的结果希望储能更少的动作，而允许系统频率偏差稍大一些。

α1和α2的值由新能源和负荷功率预测结果动态决定。在对某一时段进行优化时，如果预测到该时段下会出现较大的不平衡功率，意味着系统频率可能会产生较大的偏差，在这种情况下，α1将被调大，来保证系统频率在安全范围内；相反，如果检测到不平衡功率较小，α2则会被调大，因为该时段下频率偏移情况不会很严重。式（11）—（13）所示即为α1和α2的计算方法：

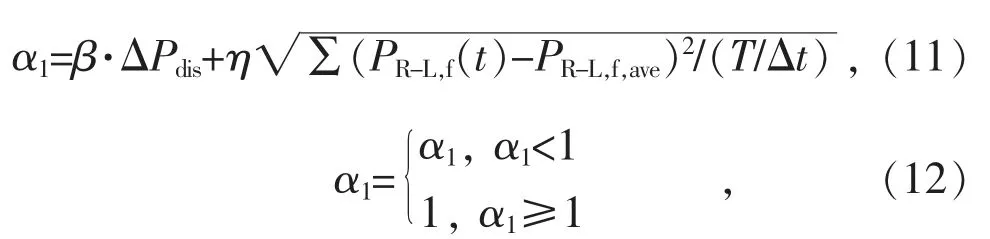
式中：η，β 为可调控参数，满足0＜η≤1，0≤β≤1；PR-L，f，ave为PR-L，f的平均值；T 表示待优化时段，T≤24 h。

目标函数满足以下约束：

式中：Δfad，max为系统允许的最大频率偏差。该限制保证频率偏差维持在安全稳定范围内。

在系统运行中，储能也要满足以下能量约束：

式中：Ee（t）为t 时刻储能能量；θc，θd分别为储能充、放电效率；El，Eh分别为储能能量的下限与上限；Δt 为仿真步长。

考虑到复杂的非线性约束，采用遗传算法来求解模型，流程如图4 所示。

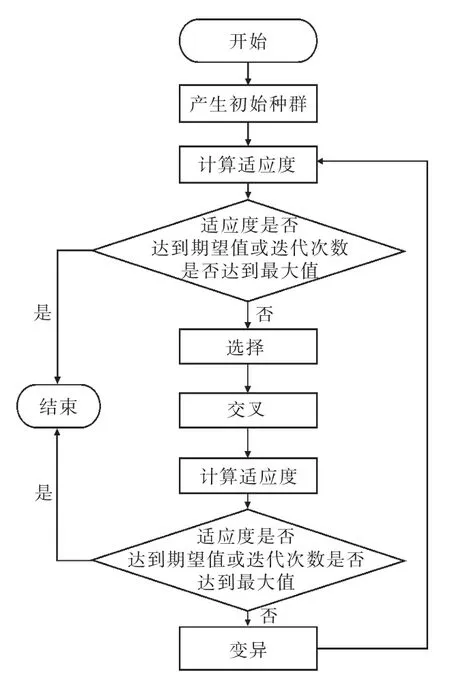
图4 算法流程

2 算例分析

2.1 仿真系统设计

基于浙江电网BPA 数据获取电力系统频率响应离散化建模所需要的数据，由此对浙江电网建立统一频率模型。在此基础上对浙江电网进行频率仿真，模拟浙江电网发生典型故障，检验储能的调频效果。在验证储能的调频能力后，基于浙江电网的预测数据对储能的调频死区和调差率进行动态优化，并与固定参数策略进行对比，以检验所提方法的优越性。

2.2 储能电站调频效果分析

为分析储能电站的调频效果，对储能参与一次调频的控制参数设置为相对保守的数值。假设浙江电网共有250 MW/500 MWh 的储能电站，调差率和调频死区分别设置为2%和0.02 Hz，模拟系统在运行第4 s 时，出现负荷突变扰动，功率缺额为800 MW，得到有、无储能参与一次调频时的频率仿真情况，如图5 所示。由图可知储能参与一次调频后系统频率最大偏移量从0.12 Hz降到0.08 Hz。

图5 出现负荷突变后的频率仿真

可以得出结论，在系统出现扰动时，储能参与一次调频能够更好地维持系统频率稳定，保证系统的安全运行。

2.3 储能调频参数动态优化

2.3.1 调频效果评估指标

为验证所提方法能够有效地提高储能经济性和功能性，本文定义频率偏差、储能动作程度指标，用以评估不同策略的控制效果，指标越小效果越好。指标包括最大频率偏差、频率总体偏移情况、储能总体响应情况以及频率-储能动作综合指标，其中最大频率偏差和频率总体偏移情况衡量储能的调频效果；储能总体响应情况衡量储能的经济性；最后通过综合指标衡量储能考虑调频效果和经济性的综合性能。定义控制效果评估指标分别如式（16）—（19）所示：

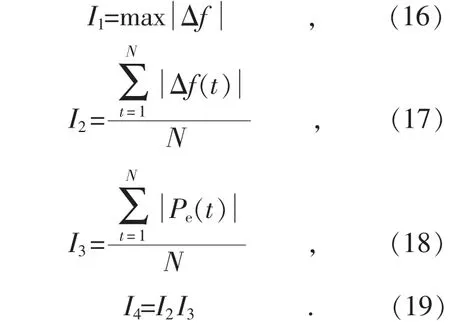
2.3.2 仿真分析

为验证所提方法能够在不同工况下兼顾储能的经济性和功能性，本文分别选取两个时段作为待优化时段。其中，时段1 功率波动较为剧烈，时段2 功率波动相对平缓。同样假设浙江电网共有250 MW/500 MWh 的储能电站。

由于本策略优化周期与经济调度保持一致，因此认为在优化时段初始时刻可再生能源-负荷综合功率的不平衡功率为0。时段1 的综合预测发电功率PR-L，f的波动情况如图6 所示。

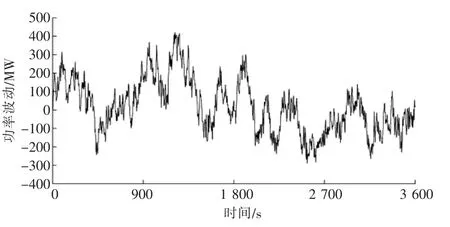
图6 时段1 的综合预测功率波动情况

由于该时段功率波动较为剧烈，储能在所提方法下将以调控频率为主要目标，储能多动作以维持频率稳定。通过仿真得到在所提策略与对比策略（固定参数）下的储能动作曲线和系统频率波动情况，如图7、8 所示。

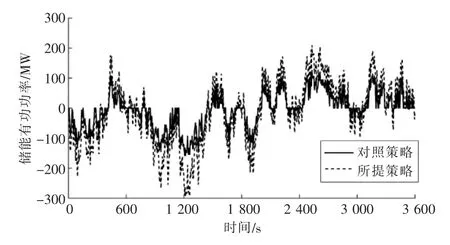
图7 时段1 的储能动作曲线

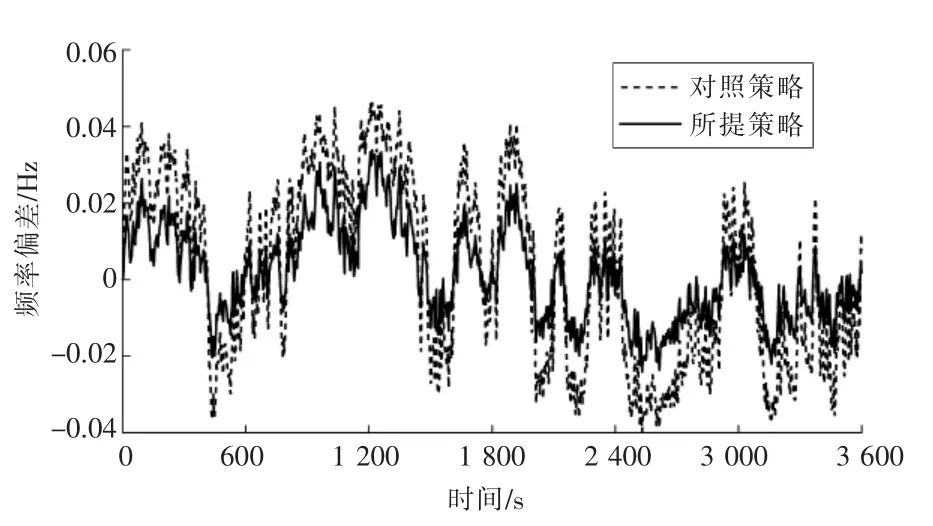
图8 时段1 的频率波动曲线

通过仿真结果可知，在该优化时段，与对照策略相比，储能在所提策略下出力较多，能过够更好地维持系统的频率稳定。

时段2 的综合预测功率波动情况如图9 所示。由于该优化时段功率波动较小，在所提策略下储能将更加注重经济型，同时保证具备一定的调频效果。

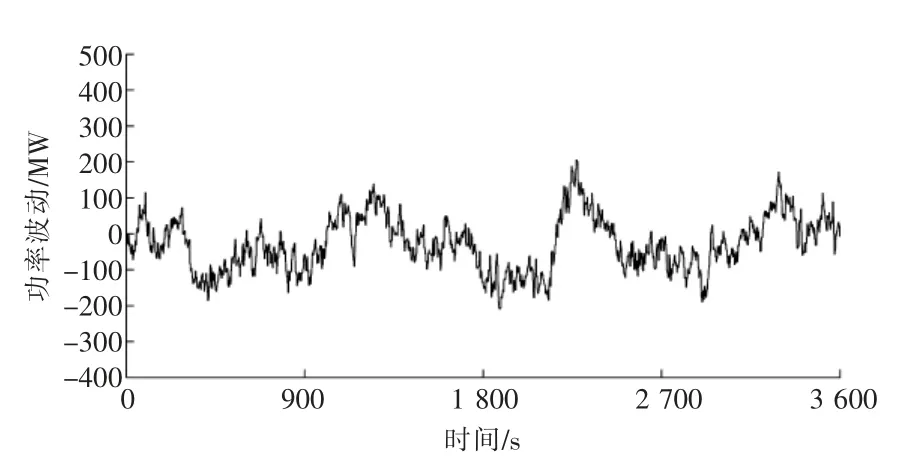
图9 时段2 的综合预测功率波动情况

同样，通过仿真得到在所提策略和对照策略的储能动作情况和系统频率波动情况，如图10、11 所示。

图10 时段2 的储能动作曲线

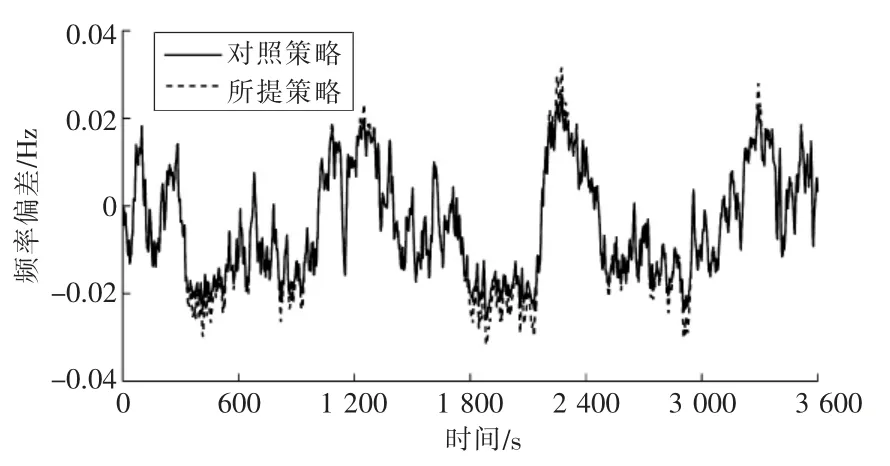
图11 时段2 的系统频率波动曲线

从仿真结果可知，在该优化时段，与对照策略相比，在所提策略下储能能够在较小出力的情况下保证调频效果。

通过比较两次仿真结果的效果评估指标能够更加直观地展示本文所提策略的优越性，评估指标结果如表1 所示。由表1 可知，在功率波动较为剧烈的场景中，所提策略的最大频率偏差为0.032 2 Hz，而对照策略为0.049 7 Hz，所提策略的频率总体偏移指标为0.009 5 Hz，而对照策略为0.022 2 Hz，说明所提策略的频率控制效果远好于对照策略。所提策略的频率-储能动作综合指标为0.793 7，而对照策略为0.923 1，说明所提策略具有更好的综合性能；在功率波动程度较弱的场景中，所提策略的储能总体响应指标为7.171 21，而对照策略为10.152 1，所提策略的储能动作程度小于对照策略，具有更好的运行经济性。所提策略的频率-储能动作综合指标为0.099 5，而对照策略为0.120 8，因此，所提策略兼顾了频率偏差与储能动作程度，无论是波动程度较强还是较弱的场景，均具有更好的综合性能。

表1 两个优化时段的储能评估指标情况

3 结论

本文通过搭建浙江电网统一频率模型，模拟浙江电网出现负荷波动，在有无储能参与一次调频时的系统频率波动情况，以此验证储能的调频效果；基于上述结果，提出动态调整储能调频死区和调差率的优化方法，能够在不同工况下满足储能经济性和功能性的需求。并基于浙江电网进行仿真，通过与对照策略进行效果评估指标比较，验证了本文所提策略能够更好地提升储能的经济性和调频能力，同时得出以下结论：

（1）在功率波动较为剧烈的场景下，系统所提策略的最大频率偏差为0.032 2 Hz，而对照策略为0.049 7 Hz，储能在所提策略下能够更好地抑制系统频率波动。

（2）在功率波动较为平缓的场景下，所提策略的储能总体响应指标为7.171 21 MW，而对照策略为10.152 1 MW，储能在所提策略下具有更好的经济性。