巡天相机旋转对开式机械快门激振力的补偿抑制
梁伟,秦开宇,蒋仁奎,刘盾
(1.电子科技大学航空航天学院 成都 611731;2.中国科学院光电技术研究所 成都 610209)
巡天望远镜主镜口径达到2m,是中国第一个大口径、大视场空间天文望远镜。巡天相机是巡天望远镜最重要的科学终端载荷之一。巡天相机焦面尺寸达到610mm×590mm,采用机械快门对焦平面进行曝光控制。在轨工作10 年,曝光次数约为100 万次,寿命长、可靠性高。快门采用结构简单、电机直驱的旋转对开结构形式。机械快门运行的旋转运动将形成微振动,产生激振力。同时方向相反的两旋转运动带来的激振力在转轴相对方向的分量抵消,在两转轴平面法向的分量加倍,成为巡天相机的主要扰动源之一,降低空间光学望远镜的成像质量,需对其进行抑制[1-2]。
类似旋转对开式机构在空间望远镜上应用较多,如哈勃望远镜(Hubble space telescope)[3-4]、钱德拉X 射线太空望远镜(Chandra X-ray observatory)[5-7]、伦琴X 射线天文台(Rosat)[8-9]和XMM 牛顿卫星(X-ray multi-mirror mission)[10-11]的遮光盖系统。这些遮光系统的功能主要是避免望远镜内部器件受到强光照射,工作过程中望远镜焦面组件未工作,运行中的激振力不影响望远镜成像质量。欧几里得空间望远镜(Euclid space mission)[12-14]中可见光成像仪(Euclid-VIS)采用的快门形式与巡天相机机械快门类似,通过在叶片后端进行严格的静动平衡设计,抑制激振力,取得了很好的抑制效果。巡天相机机械快门由于空间包络约束限制难以采取静、动平衡措施减小激振力。快门的运行频率f小于1Hz,采用传统的隔振措施,隔振频率小于0.707f时才会发挥隔振效果[15-16],这将削弱快门的支撑刚度,稳定性差。
针对旋转对开式机械快门的激振力问题,建立转子及机械快门运动数学模型,得到快门运动的激振力数值解。在此基础上,提出一种动态补偿方法用于激振力抑制:结合凸轮运动动态性和杠杆反向补偿、放大原理,且杠杆惯性力与快门激振力相等,实现激振力动态补偿抑制。采用单纯形法进行凸轮曲线优化设计。最后进行运动学仿真对激振力的动态补偿抑制方法进行验证。
1 巡天相机机械快门及其布局
如图1 所示,机械快门位于焦面组件前端,与焦面组件一同安装在主体结构上,快门两叶片同时开合实现对焦平面的曝光控制。

图1 巡天相机及机械快门布局
机械快门由正Y侧、负Y侧以及支座组成,正Y侧和负Y侧快门两叶片同步反向转动,完成快门的开启或关闭功能。
2 数学建模
2.1 旋转转子数学建模
转子绕转轴旋转,假设其满足如下条件:
1)转子与转轴均为刚性体,为薄圆盘转子;
2)在均质圆盘上附加偏心质量为m,偏心距为r。
为建立转子数学模型,采用如图2 所示的直角坐标系oxyz,转轴与坐标系x轴重合。

图2 圆盘转子模型
转子圆盘形心为O点,质心为C点,其坐标关系为:

式中,质心坐标为(xc,yc),对上式求导数,得到偏心质量的速度与加速度如下:

由于存在偏心质量m,转子的激振力如下:

2.2 机械快门运动数学模型
机械快门简化模型如图3 所示,规定叶片与水平面夹角θ 为叶片转角。当θ=0°时,快门完全关闭,当θ=90°时,快门完全打开。

图3 巡天相机机械快门简化模型
将叶片偏心简化为质点,附加质量为m,质心与转轴的距离为r。
据图3,负Y侧快门的数学模型如下:

同样,正Y侧快门的数学模型:
则机械快门的整体振动受力为:

即旋转对开式机械快门在Y向激振力相互抵消,为0;在Z向的激振力为单侧旋转运动激振力的两倍。
2.3 机械快门运动分析结果
据巡天任务规划,快门典型运行过程:1)打开和关闭过程时间为1.3s;2)保持打开持续时间为150~200s。为保证快门开启和关闭时刻的平稳性,叶片采用正弦波加减速驱动模式,即:

叶片运动曲线如图4 所示。叶片相对转轴附加质量m为1.4kg,叶片质心与转轴的距离r为144.75mm,将式(10)~式(12)代入式(9),得到一个曝光周期下快门的Z向激振力,激振力幅值达到2.38N。

图4 快门叶片驱动模式
3 法向激振力补偿抑制
3.1 补偿抑制方法
杠杆工作原理如图5 所示。

图5 杠杆工作原理图

当质点m1沿正Y向以加速度a1运动时,受到的惯性力F1为:
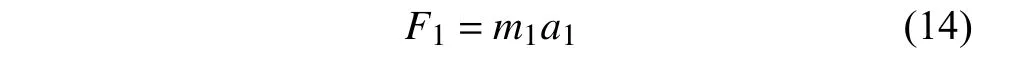
根据杠杆原理,质点m2沿负Y向以加速度a2运动,受到的惯性力F2,两者关系为:

由式(13)、式(15)知,杠杆加减速过程中,两侧角加速度大小相等,方向相反。杠杆两侧端点处线加速度方向仍相反,大小与支点距离成正比。
由式(14)、式(15)知,当快门转轴带动质点m1向上运动时,杠杆另一侧质点m2向下运动,惯性力F2与F1方向相反,可以补偿快门在F1方向上产生的激振力。杠杆在放大质点m2线加速度的同时,取m1<
3.2X 向附加分量
由图5 所示,杠杆在补偿机械快门Y向激振力的同时,将产生X向的水平分力。

其合力为:

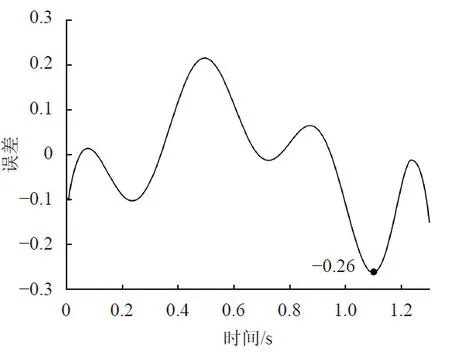
式中,m1< 考虑使用两套机构,对称布置在旋转轴下方,如图6 所示,不占用巡天相机的其他空间。 图6 补偿抑制机构布局 当两机构完全一致时,负X侧的机构产生正X向的附加分量,正X侧的机构产生负X向的附加分量,两者大小一致,相互抵消,克服补偿抑制X向附加分量不为零的问题。 两组凸轮杠杆机构位于单侧快门基座下方,如图7 所示,每套机构均由平衡块、杠杆、转轴、凸轮和导向杆组成。快门轴系与凸轮相连,无需额外驱动,轴系带动凸轮转动,凸轮驱动导向杆移动,导向杆推动杠杆一端使其绕转轴转动,杠杆另一端与平衡块相连,杠杆转动同时带动平衡块实现相应运动。 据图7 中激振力抑制机构的零件几何位置关系,假设转轴中心到导杆中心线的距离为A,到平衡块质心的距离为B;平衡块质量为m0;凸轮对导向杆的驱动位移量为k(t)。 图7 激振力抑制机构剖视图 凸轮驱动导杆移动时,k(t)随时间变化,杠杆另一端的平衡块带来的惯性力为: 式中,m0=2kg;A=35mm;B=180mm。 为了补偿快门Z向的激振力,需满足: 将式(9)~式(12)、式(18)代入式(19),即可形成凸轮驱动位移与时间的关系式,但该关系式复杂,无法求出k(t)的显性解析式,采用数值优化方式对其进行求解。 将k(t)表示成多项式: k(t)的约束条件为: 3 个约束条件分别表示:1)快门处于关闭位置时,杠杆平行于快门轴系;2)快门启动时刻凸轮驱动导向杆的速度为零;3)快门关闭时凸轮驱动导向杆的速度为零。 将快门激振力和平衡块惯性力最大差异的绝对值最小作为优化目标,即: 由于优化目标值无法求导,常规的梯度优化方法如坐标轮换法、最速下降法、牛顿法、共轭梯度法和变尺度法均不适用[17]。单纯形法作为非梯度优化方法[18],收敛速度快,稳定性好,变量个数不受限,可通过变换初始顶点避免局部最优,适用于凸轮曲线的优化。为避免陷入局部最优解,在可行域内随机初始顶点,并多次计算,选择所有计算结果中的最优值。 将式(9)、式(18)和式(20)代入式(22)中,采用单纯形法对多项式中各个参数进行优化,使M最小。随着优化变量个数增多,k(t)自由度增加,目标函数最优解越来越小,迭代次数和计算时间增加。当目标值变化率趋近于零,停止优化迭代,迭代过程如图8 所示,其中优化后目标值未超过0.26N,优化变量个数为8;将式(21)代入式(20)得到3 个方程可以解得3 项系数值,这样式(20)共11 个系数项,次数n为10。 图8 目标优化过程 优化所得多项式的各系数值如表1 所示,即凸轮驱动曲线是时间变量的10 次多项式。 表1 多项式系数 将各变量代入式(20),联合式(9)和式(12),得到凸轮转动角度与驱动位移量的关系,如图9所示。 图9 凸轮曲线 得到凸轮驱动位移曲线k(t)和线加速度曲线(t)后,可以计算惯性力与激振力之间补偿误差如下: 补偿抑制误差曲线如图10 所示,最大值为0.26N,为最大激振力的10.9%。 图10 补偿误差曲线 补偿抑制机构是一被动运动机构,不需要增加额外的电学控制系统,但会增加结构的复杂性:包括凸轮和转轴等,均为工程上的常用机构,且这些机构在航空航天任务中均得到应用[19],是可行的。对补偿抑制机构进行质量统计:单侧快门两平衡块质量小计2.0kg、机构其他部分质量为0.58kg,所以机械快门两侧机构共计5.16kg。而机械快门本体质量为17.8kg。增加补偿抑制机构后的机械快门质量共计22.96kg,增加了29.0%。其中任务总体分配给机械快门的质量要求不超过25kg,较机械快门质量仍有余量2.04kg,满足任务指标要求。因此,采用补偿抑制机构来解决机械快门微振动抑制问题,除了增加质量代价外,没有对望远镜正常工作产生其他影响,在工程上是可行的。 建立快门运动学模型对其进行瞬态分析,模拟快门运行过程。使用旋转副模拟轴系轴承,采用接触力模拟凸轮与导杆的驱动关系,移动副约束导杆的自由度。在快门支座下建立基准,将基准与支座下表面耦合,固定基准即可对整个模型进行约束,通过读取该基准的支反力获得快门运行时的激振力。 在激振力补偿抑制机构使用前后的Z向激振力响应如图11 所示。抑制后激振力幅值最大值由2.38N 降至0.29N(与优化设计得到的最大值0.26 N 基本一致),抑制率87.8%,验证了本文提出的补偿抑制方法。 图11 抑制前和抑制后的Z 向激振力 针对巡天相机旋转对开式机械快门提出一种激振力动态补偿抑制方法。建立快门的运动数学模型,设计激振力补偿抑制装置,凸轮和杠杆机构相结合实现杠杆质量点惯性力对激振力的补偿抑制。由单纯形法优化获取凸轮曲线,最后进行机械快门运动学仿真,结果表明:在激振力抑制装置采用前后,快门激振力分别为2.38N 和0.29N,抑制率87.8%,效果明显,解决了在尺寸约束下的快门激振力抑制问题。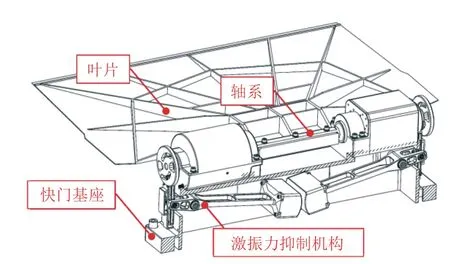
4 补偿抑制机构
4.1 机构设计
4.2 凸轮曲线优化




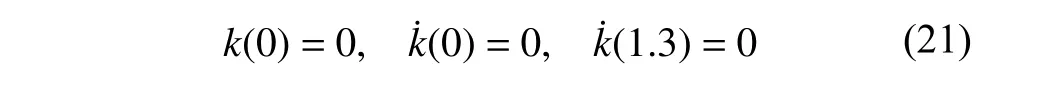



4.3 补偿抑制误差


4.4 工程可行性分析
5 运动学分析验证

6 结束语

