徐闻青安湾海滩冲流带对台风“韦帕”的波动响应特征

曾春华，胡泰桓，张会领，李志强，李高聪，田 艳

（1.广东海洋大学海洋工程学院，广东 湛江 524088；2.广东海洋大学电子与信息工程学院，广东 湛江 524088；3.河海大学港口海岸与近海工程学院，江苏 南京 210098）

冲流带是连接碎波带和陆上干滩的过渡带，海水覆盖和出露交替，使得冲流带动力地貌具有复杂的时空变异性，也是海滩泥沙输移最活跃的区域[1]，对研究岸线演变有重大意义。

冲流带现场高频观测研究展现其滩面冲淤的复杂性。Waddell[2]观测冲流带的泥沙沉积过程，发现滩面有40 s及更长周期的波动变化且沙波向岸运动。Sallenger 等[3]认为冲流带滩面的高频振动周期由下而上变长，有别于沙波向岸运动。李志龙等[4]发现冲流带滩面的长重力波频段周期性冲淤，其日内变化受潮汐控制，涨潮堆积、落潮侵蚀。冯砚青等[5]认为冲淤振动强度由下部向上部递减，长重力波起重要作用。李志强等[6]认为波群对滩面高频振动有显著影响，特别是波高大于有效波高的波群。以上冲流带滩面观测主要在常浪条件开展，而台风作用下冲流带的观测研究仍十分欠缺。常规的采集台风前后现场地形数据研究无法准确反映冲流带对台风波浪的实时响应特征[7-10]，需要进行冲流带台风期间现场高频观测研究。

冲流带在台风影响下的响应过程是一个多自由度和强非线性的系统，要深入研究其内在物理机制，须识别系统的主要模态，并将模态与相关动力因子联系起来[11-12]。本研究利用2019 年7 号台风“韦帕”影响下徐闻青安湾海滩冲流带95 组滩面变化高频数据和134 min 同步波浪数据，借助复经验正交函数（CEOF）、快速傅立叶变换（FFT）和连续小波变换方法对地形和波浪数据进行分析，开展台风作用下海滩冲流带地形主要波动模态与波浪分量之间内在联系研究，为深入研究海滩冲流带对台风响应的动力机制提供参考。

1 数据与方法

1.1 研究区域与台风“韦帕”概况

青安湾是琼州海峡北岸中部的半封闭弧形海湾（图1）。海滩的长度约1 800 m，海滩宽度60～ 80 m。潮汐类型为不规则日潮，平均潮差0.82 m，最大潮差2.16 m。常浪以E—SW 方向为主，风浪为主，涌浪为辅，平均波高小于0.35 m，平均周期约为4.0 s[13-14]。本研究观测前在冲流带表层的泥沙样品（图2 中4#桩位置）粒径范围为（0.25～ 3.75）Φ（其中Φ=−log2D50，D50为中值粒径）[15]，平均粒径为2.506Φ，主要成分为细沙[（2.25～ 3.00）Φ]，占比为90.9%。

“韦帕”是2019 年第7 号强热带风暴，形成于南海北部、青安湾东南向约600 km 处。7 月30日17 时发展为热带低压，7 月31 日6 时升级为热带风暴。8 月1 日1 时50 分在海南省文昌市首次登陆，中心附近最大风力23 m/s，8 月1 日17 时40分再次登陆广东省湛江市坡头区，中心附近最大风力23 m/s，8 月2 日21 时20 分第三次登陆广西省防城港市（图1），中心附近最大风力仍为23 m/s，8 月3 日23 时停止编号。现场测量期间（2019 年8月1 日11 时19 分至13 时33 分），“韦帕”路径与青安湾之间的最小距离约50 km。青安湾受台风7级风圈影响时段为7 月31 日20 时至8 月2 日20 时。

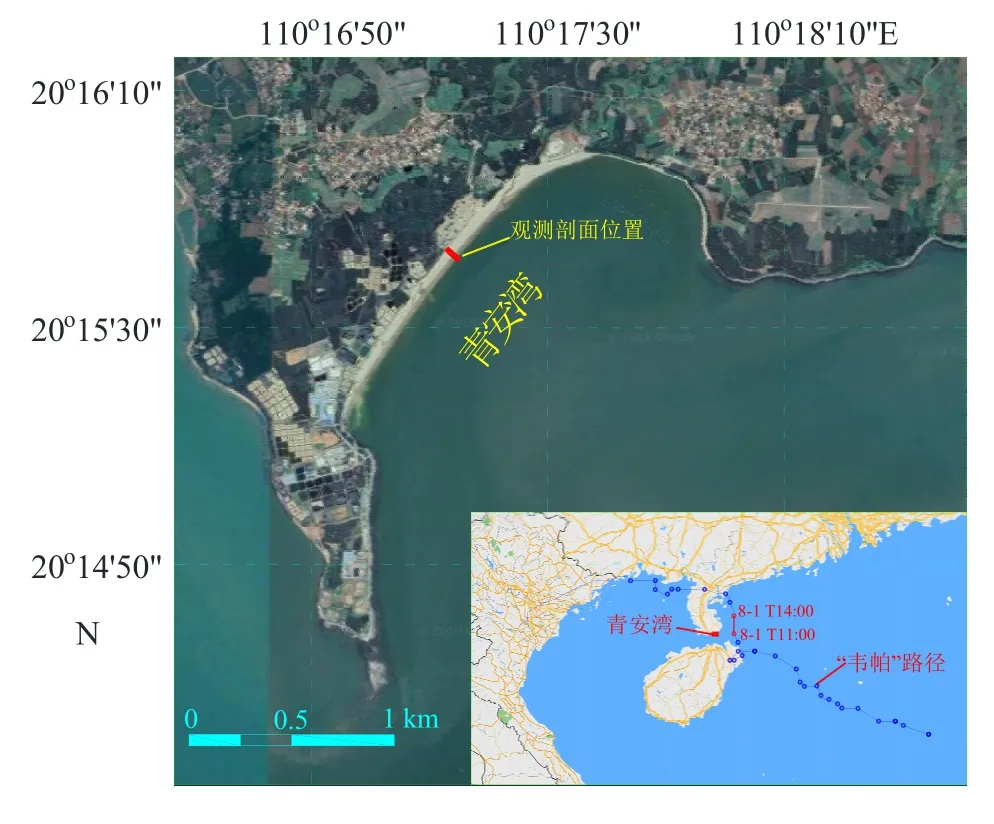
图1 研究区域和台风“韦帕”路径Fig.1 Study area and Wipha track

1.2 现场数据采集

冲流带地形变化数据通过测量参考桩高度方法获取[3,13,16]。参考桩为直径10 mm 的细钢筋，共6 根，由陆向海编号1—6#（图2）。利用全站仪将桩位置、桩顶高程与后方固定基准点关联，由测量员持钢尺沿固定方位依次循环不间断测量桩的外露高度。2019 年8 月1 日11 时19 分至13 时33 分，在134 min 内获取95 组数据。在与6#桩距离24 m处放置波潮仪（图2）采集实时海面波动数据，采样频率为4 Hz。

图2 现场测量布置剖面Fig.2 Schematic of the cross-shore beach profile and the surveying layout

1.3 数据处理方法

采用线性最小二乘法滤出潮位过程。将原始数据分成1 min 一组，对每组数据采用上跨零法计算波高和波周期。利用快速傅立叶变换（FFT）计算频谱[17]，利用连续小波变换进行时频分析。

1.3.1波浪数据谱分析 快速傅里叶变换是根据离散傅里叶变换的奇、偶、虚、实等特性，高效、快速地计算离散傅里叶变换（DFT)，离散傅里叶变换如式（1）[18]。

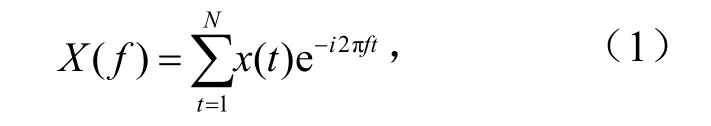
其中，x(t)为采集到的时域离散数据，f为对应的频率。

波浪功率谱密度计算如式（2）[19]。

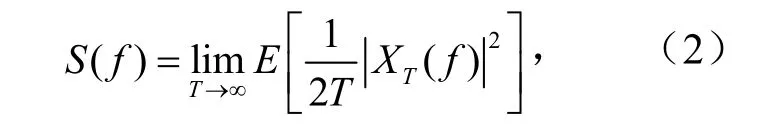
其中，S(f)是频率为f的成分对平均（时间平均）功率的贡献的平均。

1.3.2连续小波变换处理波浪数据 小波分析使得特定尺度的信号与特定的时间（位置）相关，显示传播的频率（标度）分量以及传播时间[20]，可以多分辨率分析。出发点是一个基本小波Ψ(t)，也称母小波，是具有带通性、零均值、波动性和时频局部化特性的函数，可以缩放、平移和旋转以生成自适应小波滤波器，并构造一个小波基Ψa,b(t)滤波器组，如式（3）[21]。通过母小波与分析信号的相关性在空间域中局部化频谱分析，分割整个信号。

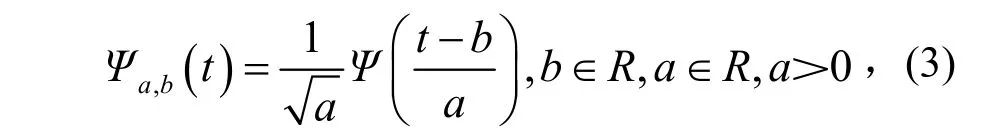
其中，a为尺度因子（与周期和频率有关），b为平移因子（时间位置）。

当研究离散信号f(nδt)（n=1,2,3,···，N；N为样本容量）时，离散小波变换（DWT），如式（4）[21]。

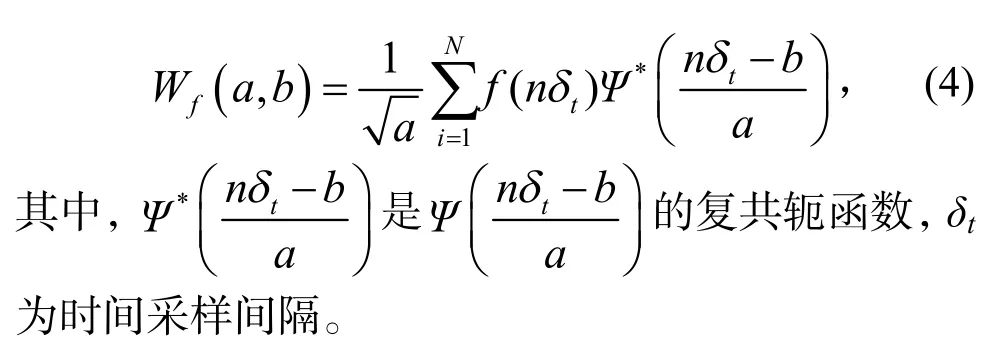
小波a的尺度参数按式（5）取值。

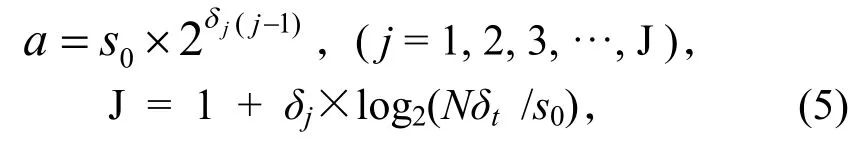
Wf(a,b)包含f(t)和Ψa,b(t)的信息，母小波的选择至关重要，本研究的母小波是Morlet 小波，该小波是高斯函数调制的连续平面波，其定义如式（6）[21]。

其中，ω0是角频率，对于Morlet 小波变换，ω0=6比较合适[22]。

1.3.3复经验正交函数方法（CEOF）处理滩面高程变化 CEOF 方法对数据集的波动特征描述更深入，有助于解释特征函数的物理意义，在海岸地形演变方面已有少量应用[23-26]。一个移行波可表示为式（7）[27]。

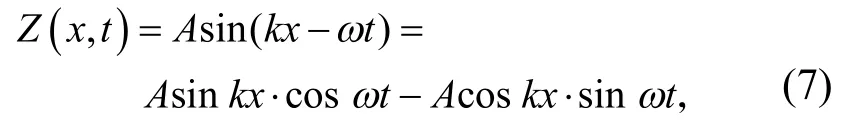
其中，振幅是A，相位是kx-ωt，kx为空间相位函数，-ωt是时间相位函数。一个传播的波需要两个空间型和两个时间系数表示，两个空间型正交并分别正比于sinkx和coskx，有相同的空间波数。两个时间系数也正交并分别正比于cosωt和-sinωt，有相同的频率（周期）。

CEOF 能表示一对正交的空间型，可通过Hilbert 变换获取。当Zt是有限长度的离散时间序列，可用式（8）的相位漂移π/2 滤波运算生成Zt的Hilbert 变换[19]。

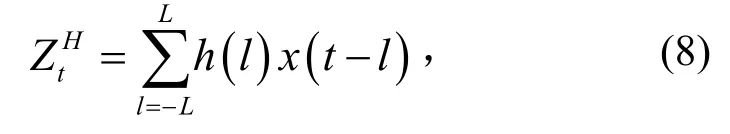
式(8)中，权重系数h(l)取值如下，

其中，L为滤波器长度，一般L取7～ 25，L取太大会损失过多信息，为保留最全的响应信息，本研究取L=7。

复值随机过程Ut在各相应桩位的分量可表示为式（9）[19]。

对于m个空间点，n个观测样本的滩面变量场，其复资料矩阵为Um×n，分解得式（10）[28]：

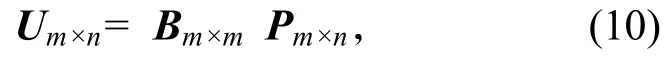
其中，B为m×m阶复空间函数矩阵，P为m×n阶复时间函数矩阵。

复空间函数矩阵由复协方差阵不同特征值的特征向量构成，在复空间函数和复时间函数基础上求出表征振荡和移动特征的空间振幅函数Sk(x)，空间相位函数Qk(x)，时间振幅函数Sk(t)和时间相位函数Qk(t)[28]，如式（11—14）。

式（11—14）中，x为空间点；t为时间点；k为特征向量序号；Bk（x）表示第k个特征值对应的特征向量；是Bk（x）的共轭向量；表示Pk（x）的共轭。

空间振幅函数Sk(x)表示第k个特征模态变率的空间分布，给出Z场空间不均匀性的测度，分析滩面变量场的空间分布结构及各位置的变化强度。

空间相位函数Qk(x)表示在不同空间点上振动的空间位相，分析波的传播方向。

时间振幅函数Sk(t)表示第k个特征模态Z场在量值上的时间变率，反映变化强度随时间的变化。

时间相位函数Qk(t)在移行波中即为-ωt，体现波的传播速度。

2 结果与分析

2.1 潮位与波浪

观测时间段（8 月1 日11:19—13:33）台风“韦帕”中心与观测点位置距离最近（图1），图3（a）显示潮位上涨约9 cm，达到当天最高潮位。

图3（b）表明显著波高H1/10范围为0.4～ 0.8 m，11:19—12:19 时段波高变化幅度逐渐变大，随后波高变化幅度逐渐变小且相对稳定。

图3 潮位与显著波高过程Fig.3 Time series of water level and mean of the highest one-tenth of wave heights

波浪频谱（图4）表明近长重力波（0.01～ 0.04 Hz）占比最大，谱峰频率为0.027 Hz。其次是重力波（＞ 0.04 Hz），谱峰频率为0.051 Hz。占比最小为远长重力波[29]（0.004～ 0.010 Hz），谱峰频率为0.009 Hz。

图4 波浪谱密度Fig.4 Wave spectral density

连续小波变换体现主要波浪分量随时间的分布情况（图5），图5 中深蓝代表波能量弱，深红代表波能量强，黑色锥形曲线标定边缘效应影响的范围，该曲线以外的波能受到边界效应的影响而不予考虑[30]。周期小于25 s 对应重力波分量（＞ 0.04 Hz），分布稳定且连续。周期32 s 附近对应近长重力波（0.01～ 0.04 Hz）分量，分布也相对均匀，在11:59 时刻和12:29 时刻附近出现明显的间断。远长重力波（0.004～ 0.010 Hz）部分对应的周期为100～250 s，其能量分布的周期范围比其他波浪分量的跨度大，在11:30 时刻附近和12:19—12:39 时段出现间断。

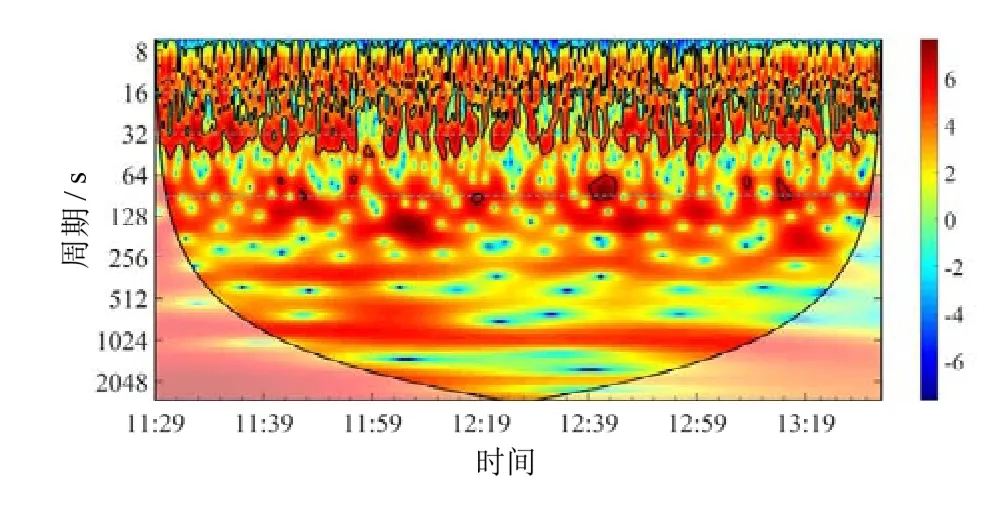
图5 波浪连续小波变换Fig.5 Wave continuous wavelet transform

2.2 冲流带滩面响应变化

冲流带滩面各桩位的地形变化幅度不同，变化最大位置为3#桩位，其次是4#桩位，2#、5#和6#桩位的变化不明显，而1#桩位几乎没有变化（图6）。

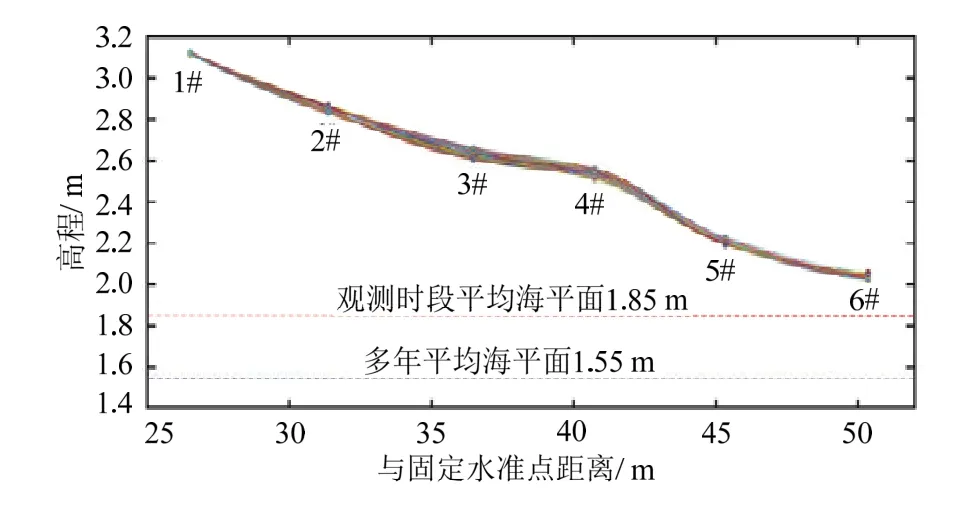
图6 实测剖面变化形态Fig.6 Variation of the cross-shore profile

原位测量表明，各桩位的地形演变趋势不同，存在侵蚀和淤积振荡交替现象（图7）。

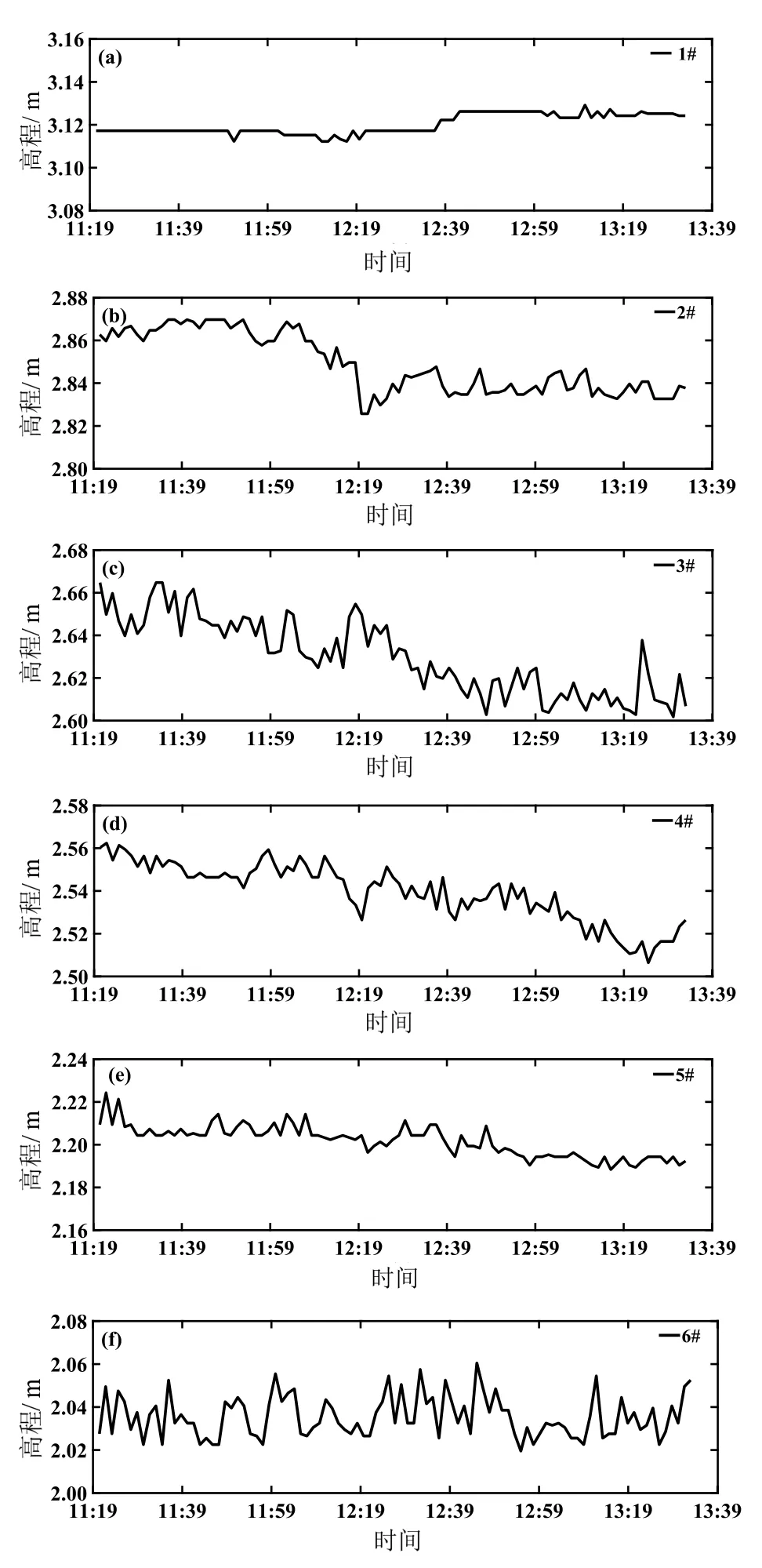
图7 各桩位高程响应过程Fig.7 Elevation processes of pegs

1#桩处于冲流带最上方，上冲流能量消耗殆尽，呈现泥沙落淤，滩面变化幅度不到2 cm。

2#桩在测量时段的前一个小时处于冲淤动态平衡状态，在2.86 m 高程上下轻微振荡。12:19 时刻产生明显侵蚀，随后保持新的动态平衡状态，在2.84 m 高程上下轻微振荡。

3#桩变化幅度约为6 cm，整体呈逐步侵蚀趋势。对照具体时刻，在11:30 时刻出现明显的淤积现象应是下方4#和5#桩位置上冲流挟带泥沙落淤。12:19时刻出现另一个明显的淤积现象，除了下方4#和5#桩位置上冲流挟带泥沙落淤，还有2#桩泥沙向海输移的贡献。

4#桩变化幅度约为5 cm，小于3#桩的变化，滩面也是逐渐蚀低但过程更平稳，只在12:19 时刻出现比其他时段更明显的侵蚀现象。

5#桩变化幅度不到2 cm，逐步侵蚀趋势，过程平稳。

6#桩处于冲流带下沿，整个过程基本呈现动态平衡状态，在2.04 m 高程上下轻微振荡，振荡幅度较大。可能是6#桩位置与碎波带相连，受下冲流与破碎带波浪交汇的影响，此处滩面泥沙运动更剧烈些。

3#桩和6#桩的振荡幅度较其他桩位大，说明这两个桩位处滩面变化都很剧烈，但两者的变化趋势截然不同，3#桩逐步侵蚀而6#桩动态平衡。其他桩位每分钟的振荡幅度都较小，但变化趋势迥异。这与Waddell[2]观测的沙波向岸运动和冯砚青等[5]观测的冲淤振动强度由滩面下部向上部递减现象皆有所不同，体现了台风波浪作用下，冲流带滩面响应灵敏且呈现出极其复杂的非线性变化。

2.3 冲流带滩面变化模态

在134 min 的观测中，6 个桩位和95 组连续高程数据集构成6 维空间和95 个矢量序列的随机场，由CEOF 分解得到的特征值如表1。

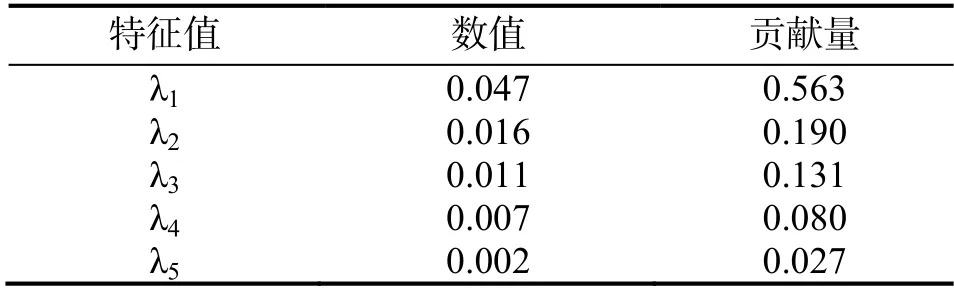
表1 特征值排序Table 1 Sorting table of eigenvalues

通常，方差三阶到五阶模态被认为足以重构任何时间序列原始数据，包含四阶模态被认为是标准的做法[14]。在本研究中，前四个模态特征值λ1—λ4的累积值占总方差的96.4%，能全面地描述台风“韦帕”影响下冲流带的响应特征。

2.3.1第一模态特征 第一模态对地形数据集的解释达56.3%。第一模态的分布和特征变化如图8。

图8 第一模态的分布和特征变化Fig.8 Spatial amplitude,spatial phase,temporal amplitude,and phase of the first mode

图8 中，空间振幅显示3#桩位振幅变率最大，向两端线性递减。空间相位图中相位正值为淤积，负值为侵蚀。时间振幅在前半段逐步减小，后半段逐渐增强，变化趋势呈准线性，说明此模态的主导动力具有持续稳定特征。时间相位12:19 时刻前为较小正值，结合空间相位图可知此时段滩面变化小、缓慢甚至有轻微的淤积；12:19 时刻之后在±π之间来回振荡，传播速度变快，先是正值的时间比负值长，但正值没达到极值+π（12:19－12:39），接着正负值时间相当且都在极值±π 来回快速切换（12:39－12:54），最后负值时间长且主要停留在-π的极值位置。说明在12:19 时刻之后滩面变化加剧，趋势由轻微淤积到淤积侵蚀交替，最后侵蚀主导。比重最大的近长重力波（图4）在连续小波变换中（图5）显示整体分布稳定，但在11:59 和12:29时刻有明显减弱，与时间振幅函数减弱时间对应，表明近长重力波是第一模态的主导波浪力。波高在12:19 之前波动大（图3(b)）造成冲流带下方的碎波带泥沙大量悬浮，近长重力波上冲流将悬沙带向岸产生淤积。12:19 之后波高变化幅度减小，悬沙量减小。近长重力波引起冲流带的泥沙向海占主导地位，侵蚀加剧。

2.3.2第二模态特征 第二模态解释了地形数据集19.0%的变化。第二模态的分布和特征变化如图9。

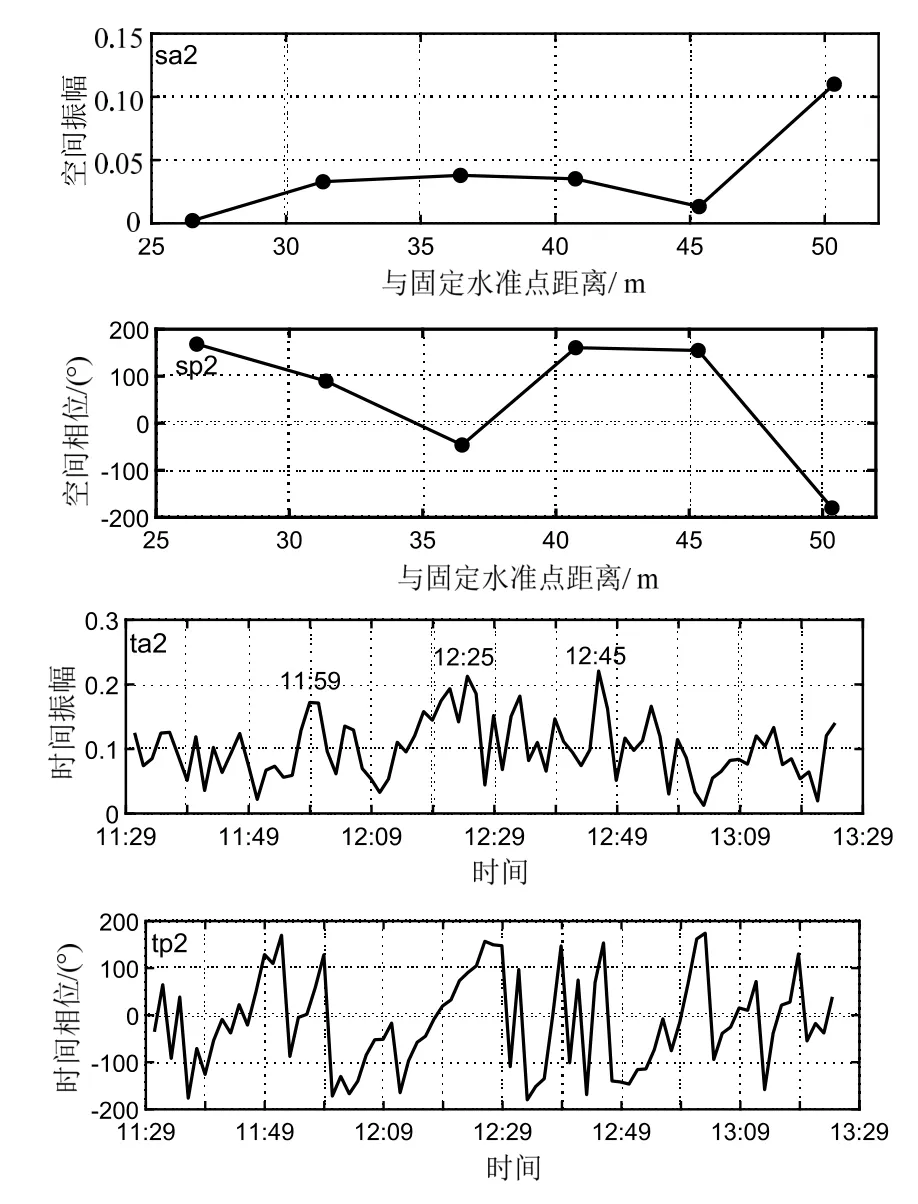
图9 第二模态的分布和特征变化Fig.9 Spatial amplitude,spatial phase,temporal amplitude,and phase of the second mode

图9 中，空间振幅显示6#桩振幅变率最大，其次是2#－4#桩位，5#桩位变化微小，1#桩位几乎无变化。空间相位图中3#和6#桩位侵蚀，其他桩位淤积。时间振幅曲线在11:59、12:25 和12:45 时刻有显著峰区。时间相位总体负值占优，由负值向正值转变缓慢，而由正值向负值转变迅速。结合空间振幅和相位，可知泥沙向海输移占优，并在3#桩位置产生分段输移现象。

在连续小波变换中（图5），近长重力波浪及远长重力波浪分量在11:59 和12:29 时刻均有减弱，但时间振幅函数相应增强，11:49、12:09、13:03 和13:23 时刻，长重力波分量均出现增强时，时间振幅函数却对应出现极小值，表明第二模态的主导波浪力为占比第二大的重力波（＞0.04 Hz）。但在12:45时刻长重力波浪分量出现最强分布时，时间振幅函数亦有突发增强，表明当长重力波足够强时，可抵消甚至短暂取代重力波的主导作用。

2.3.3第三模态特征 第三模态方差贡献率为13.1%。第三模态的分布和特征变化如图10。

图10 第三模态的分布和特征变化Fig.10 Spatial amplitude,spatial phase,temporal amplitude,and phase of the third mode

图10 中，空间振幅显示2#、3#和6#桩位振幅变率较大，其次是4#和5#桩位，1#几乎无变化。空间相位图中1#、3#和6#桩位淤积；2#、4#和5#桩位侵蚀。时间振幅在12:19 和13:12 时刻附近有显著的峰区。时间相位在12:19 时刻之前正值占优，之后负值占优，由负值向正值转变缓慢，而正值向负值转变十分迅速。结合空间振幅和空间相位，12:19时刻前3#和6#桩位有明显淤积，2#、4#和5#桩位侵蚀不明显。12:19 时刻后3#和6#桩位淤积减弱，2#、4#和5#桩位侵蚀加强。

对比波连续小波变换（图5），远长重力波在12:19 和13:12 有显著的增强，在11:50、12:30 和13:05 左右有明显的减弱，与时间函数振幅峰值和小值的时间基本一致，说明远长重力波是第三模态的主导波浪分量。

2.3.4第四模态特征 第四模态方差的贡献率只有8.0%。第四模态的分布和特征变化如图11。

图11 第四模态的分布和特征变化Fig.11 Spatial amplitude,spatial phase,temporal amplitude,and phase of the fourth mode

图11 中，空间振幅显示2#和4#桩位振幅变率较大，3#、5#和6#桩位变化微小，1#几乎没变化。空间相位图中1#、3#和4#桩位淤积；5#桩位侵蚀，2#和6#桩位的相位为零。时间振幅曲线在12:12 和13:12 有稍明显峰区。时间相位无明显规律，转换显得比较凌乱。结合空间振幅和相位，表明冲流带滩面中下部振荡较明显，上部变化微小。

对比波连续小波变换（图5），在11:55、12:20、12:50和13:20时刻长重力波分布弱，时间振幅最强，11:42、12:09、12:30、12:50 和13:15，远长重力波分布强，时间振幅出现极小值。说明第四模态主要波浪动力成分为重力波（＞0.04 Hz），主导滩面响应中不规则的微幅振荡。

3 讨论

3.1 冲流过程的影响

观测后冲流带表层泥沙采样的粒径范围为（1.00～ 4.00）Φ，平均粒径2.613Φ，主要成分为细沙（2.25～ 3.00）Φ，占比为96.1%，冲流带表层泥沙粒径呈细化现象。第1 组和第95 组剖面数据的平均坡度由1∶22 转为1∶22.4，坡度趋于平缓。悬浮泥沙被上冲流携带向岸致冲流带淤积，快速回流下冲引起泥沙向海输移而致冲流带侵蚀。单个冲刷事件包括三个不同的阶段：上冲、回流和下冲。每个波浪分量在冲流带既有淤积又有侵蚀作用。在上冲过程中，在上冲达到其最高范围之前，冲流带中下部的水流通常会逆转[1]，可能是上方下冲流的冲撞引起的水跃使得下方上冲及上方离岸悬沙均落淤，或是部分波长短周期小的重力波能量消耗快而导致泥沙落淤。所以在冲流带下部，冲流频率较高，滩面变化也更为活跃，这与Sallenger 等[3]观测到冲流带振动周期由下而上变长的研究结论相似，这也应是3—6#桩位振荡幅度更大、第二和三模态中出现分段式侵蚀淤积现象的原因。另外受坡度影响，不同粒径的泥沙均向海输移，粗颗粒向岸输移比向海输移的难度要大，导致上冲细颗粒成分更多，导致冲流带表层泥沙的细化。在测量期间，冲流带经历了淤积、侵蚀和稳定阶段。这与Masselink等[31]在法国高能沙滩Truc Vert 冲流带及海岸线侵蚀淤积过程对波浪和潮汐条件变化响应的现场调查研究结果一致。

3.2 波浪分量相互作用对滩面波动响应的影响

波浪在碎波带触底并掀沙，波高越大，掀沙强度越大，波高稳定，剖面变化适应波高后，掀沙减少，如果波高的再次变大，可使掀沙再次增强，这是各模态中冲流带淤积现象的主要悬沙来源。破碎后的入射波能随着惯性继续向岸传播，传播过程中重力波能不断耗散。而长重力波近岸波高随波浪的向岸传播加大，波能也加强[32]。因此，在风暴条件下，长重力波是泥沙输移的主导因素[33-35]。另外，重力波的波长较短和周期较小，可在冲流带范围内同时出现多个波浪，它们在冲流带的超越、上冲、趟流和下冲碰撞，导致了冲流带滩面复杂的非线性变化[36]。冲流带内悬沙的输移方向不仅取决于水流的湍流性质、流速和泥沙沉降速度，还取决于波浪分量的相互作用和碰撞之后的“净能量”[37]。而这种强弱对比在时空分布是极度不均匀的，第一模态中近长重力波足够强时，重力波的影响不足以改变各桩位的侵蚀淤积趋势，冲流带的冲淤呈现整体一致，各桩位的空间相位方向相同。当长重力波与重力波对比减弱时，冲流带各桩位的响应就会出现不一致现象，如第二到第四模态中，各桩的空间相位幅度和方向各异，波浪分量的相互作用效果显著。

4 结论

通过对台风“韦帕”期间徐闻青安湾海滩冲流带滩面波动高频数据和实时连续波浪数据分析，得出以下结论：

1）台风期间碎波带波谱为多谱峰，主要由近长重力波、远长重力波和重力波三个波分量组成。近长重力波所占的比例最大，其次是重力波，最后是远长重力波。

2）冲流带在台风波浪作用下，不同位置冲淤响应各异，冲流带中部的侵蚀较明显，两端的侵蚀幅度较小，冲流带中下部振荡剧烈。

3）冲流带对台风“韦帕”响应的波动特征由四个模态组成（累积方差为96.4%）。第一模态解释56.3%的冲流带滩面变化，主要由近长重力波主导。第二模态方差占比19.0%，由重力波控制。第三模态方差占比13.1%，由远长重力波控制。第四模态方差占比8.0%，主导波分量是重力波。长重力波控制冲流带的泥沙向海输移，重力波主导泥沙输移的振荡成分，各波浪分量强度随机变化且相互影响，导致冲流带滩面的复杂变化。