Exponential Synchronization of Competitive Neural Networks with Time Delay under Intermittent Control∗
MEI Xuehui,LIU Bao,WU Lijun
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract:In this paper,the problem about the exponential synchronization of competitive neural networks with time delay under intermittent control is discussed.By using Lyapunov function method and differential inequality method,some sufficient conditions are given which are based on global exponential synchronization of competitive neural networks with large time delay and small time delay,and the corresponding criterion is established.Finally,a numerical example is shown to verify the correctness and validity of the theoretical result.
Key words:competitive neural networks;synchronization;time-varying delay;intermittent control
0 Introduction
Competitive neural networks model is an important kind of unsupervised synaptic modification neural network,which contains two state variables:short-term memory variable(STM)to describe fast neural activities,and long-term memory variable(LTM)to describe slow neural activities.Since Cohen and Grossberg[1]first proposed the competitive neural networks in 1983,there have been many works about the competitive neural networks,such as competing neural networks with different time scales[2−5],time-varying distributed competitive neural networks with time delay[6,7],unsupervised competitive neural networks[8],competitive neural networks with different time scales and random disturbances[9],delay competitive neural networks with discontinuous activation function[10],competitive neural networks with different time scales and time-varying delays[11].
In addition,synchronization is a typical collective behavior,which is widely used in biological evolution,chemical reaction,safety communication and so on.Since the pioneering works of Pecora and Carroll[12],and the synchronization of competitive neural networks has attracted more and more attentions.In[4],Lou and Cui studied the exponential synchronization of a class of competitive neural networks,and designed some exponential synchronization criteria by using Lyapunov function,linear matrix inequality method and Newton-Leibniz formula.In[9],an adaptive feedback controller was designed by Gu to realize the complete synchronization of the coupled time-delay competitive neural networks with different time scales and random disturbances.By using the LaSalle invariance principle of stochastic differential delay equations,the globally certain asymptotic stability of error dynamic systems was studied.In[11],Gan studied the synchronization of a class of competitive neural networks with different time scales and time-varying delays.He proposed a new delay partition method and derived a delay correlation condition to ensure the synchronization of response system and drive system.By solving LMI,the design of gain matrix of linear feedback controller can be realized.In[13],Zhang et al studied the synchronization problem of dynamic networks under hybrid impulse and switch control.The results show that collective synchronous motion appeared in many large-scale dynamical networks.Based on the concept of impulse control and the stability theory of the impulse system,a new criterion of impulse synchronization for the model was established.
In recent years,discontinuous feedback control strategies such as intermittent control have been widely used in traffic systems,communication and other fileds[14−16].Therefore,it is necessary to study the intermittent control methods.For example,in[17],periodic intermittent nonlinear feedback control method is used to synchronize a class of nonlinear chaotic systems with time delay.Based on Lyapunov functional theory and Halaner inequality,some synchronization criteria were derived and sufficient conditions were obtained to guarantee delay-free synchronization of nonlinear systems.In [18],the problem of exponential stability for a class of nonlinear systems was studied by means of periodic intermittent control.In this paper,Li et al.gave a set of exponential stability criteria for linear matrix inequalities,and a simple sufficient condition determined by three scalar inequalities.On the premise that the control period and control width were fixed and known,a suboptimal intermittent controller was designed for the general cost function and the theoretical results were verified by numerical simulation.In [19],the exponential stability of delayed chaotic neural network was studied by using periodic intermittent control method.Using Lyapunov function and Halaner inequality,the authors established the exponential stability criterion and its simplified form of the controlled neural networks.The feasible region of control parameters was estimated strictly.The theoretical results and numerical simulation show that the continuous time DCNN could be stabilized by using the non-zero duration intermittent feedback control.
Based on the above discussion,we consider the competitive neural networks model with time-varying delay.By using Lyapunov function method and differential inequality analysis method,the global exponential synchronization conditions of competitive neural networks with time delay are discussed,and the corresponding criteria are established.At the same time,we studied the exponential synchronization problems of competitive neural networks with both large and small time delays and intermittent control,and some sufficient conditions are established.Finally,a numerical example is shown to verify the correctness and validity of the theoretical result.
1 Model building and preliminaries
Consider the following competitive neural networks with time delay
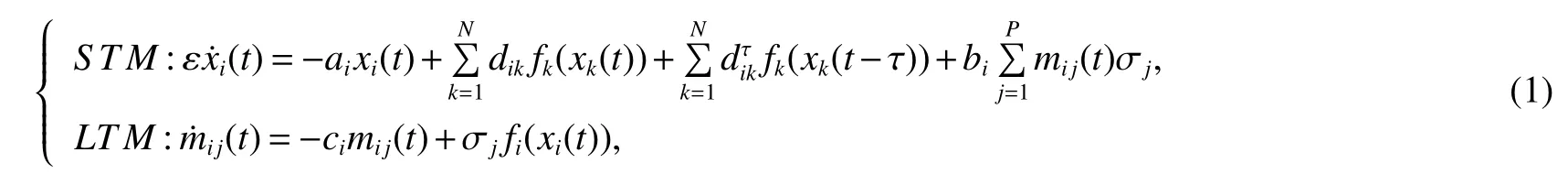
whereNis the number of junction neurons in STM state,Pis the number of neurons stimulated by external stimulation,xiindicates the current activation level of neurons,fi(·)represents the neuron output function,mi j(t)is recorded as a valid join,σjis recorded as external stimulus weight,ai>0 is called the neuron activation constant,ci>0 is any constant,dikrepresents the connection weight between thei-th andk-th neurons,birepresents the degree of external stimulation,ε>0 represents the time scale in the STM state,τ is a delay constant:represents the connection weight of the delay feedback between thei-th andk-th neurons.
Letsi(t)==mi(t)σ,where σ=(σ1,σ2,…,σP)T,mi(t)=(mi1(t),mi2(t),…,miP(t))T,then the system(1)can be represented as follows
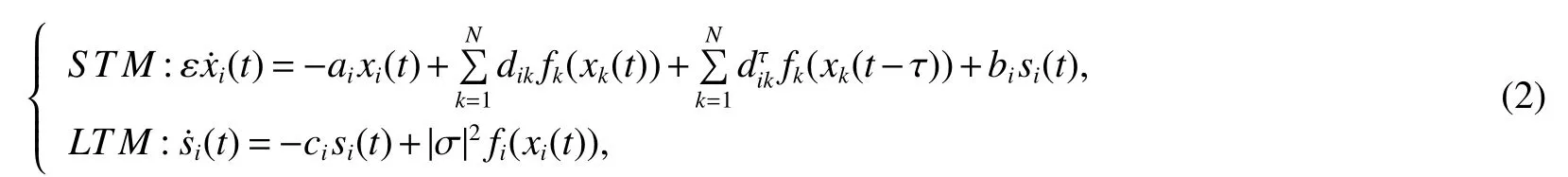
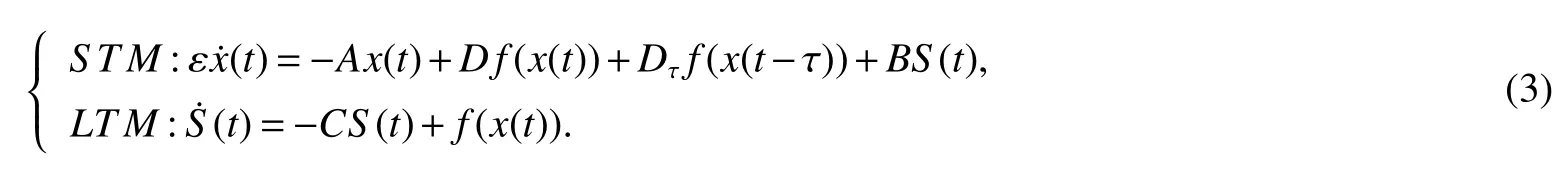
Therefore,the system is described as follows
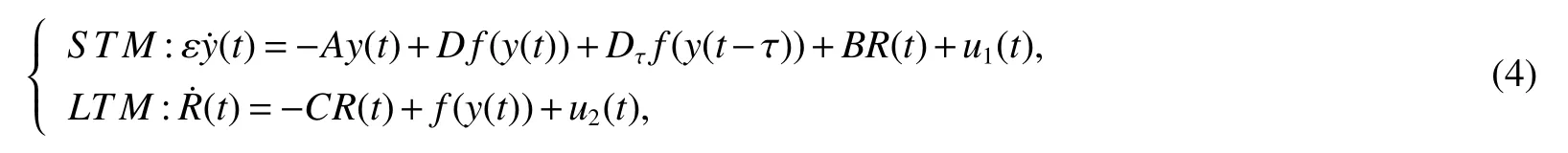
wherey(t)=(y1(t),y2(t),…,yN(t))T,R(t)=(r1(t),r2(t),…,rN(t))T,ui(t)(i=1,2)is an intermittent controller
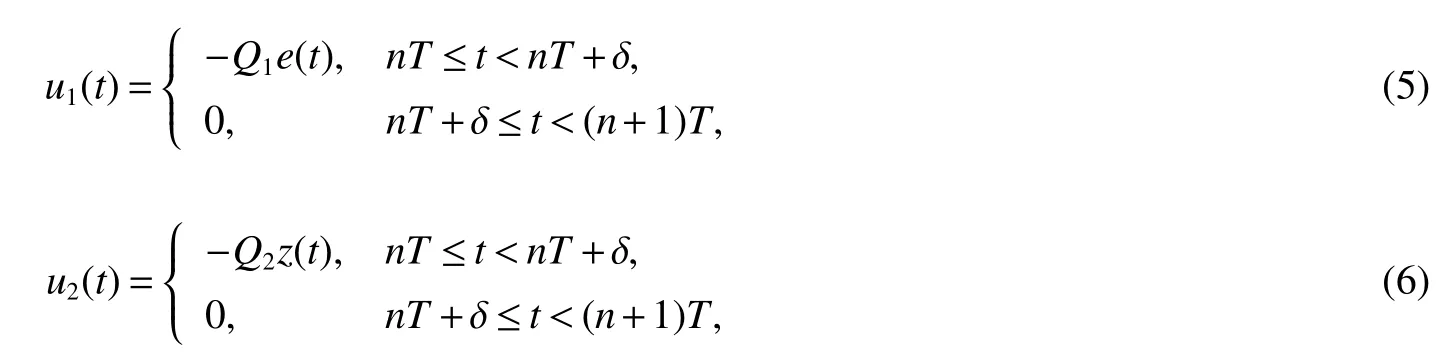
Qi∈RN×N(i=1,2)is the gain matrix of feedback control.Lete(t)=y(t)−x(t),z(t)=R(t)−S(t),then the error dynamic system can be written as
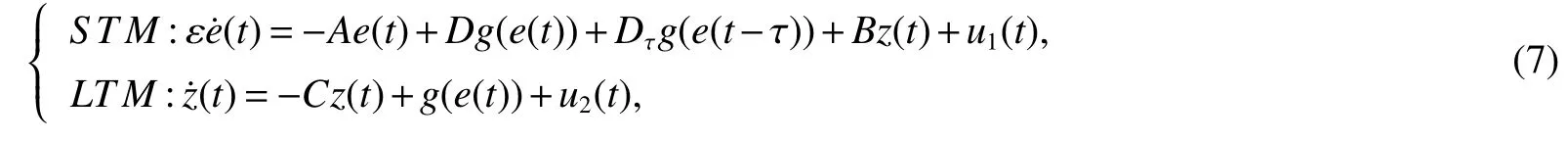
whereg(e(t))=f(y(t))−f(x(t)),g(e(t−τ))=f(y(t−τ))−f(x(t−τ)).
Assuming 1There is a symmetric positive definite matrixL=(lij)m×n,for anyx,y∈Rn,we have‖f(x)−f(y)‖≤L‖x−y‖.
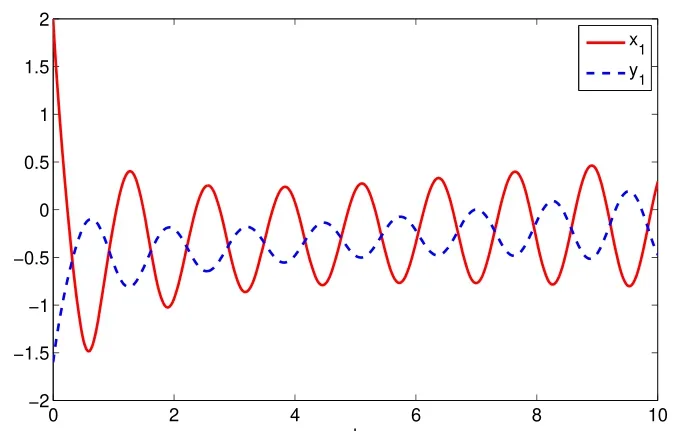
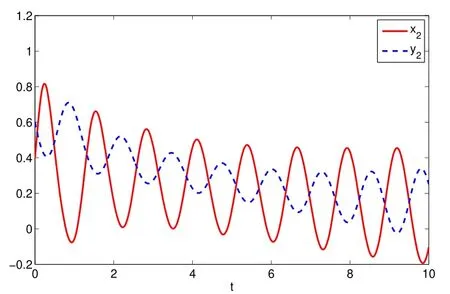
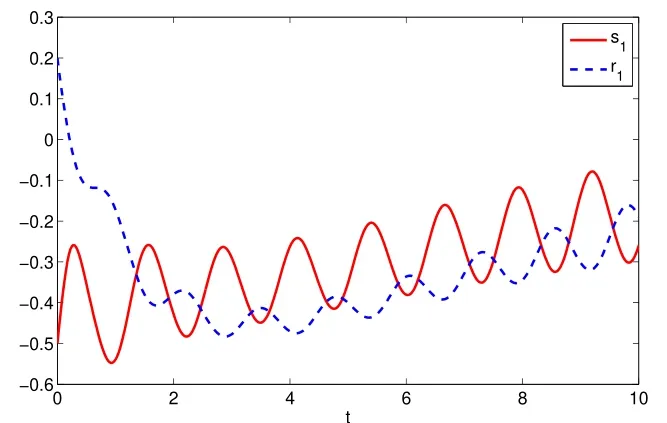
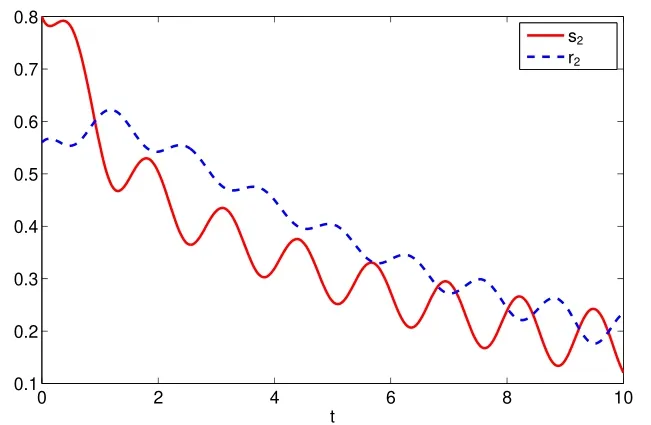
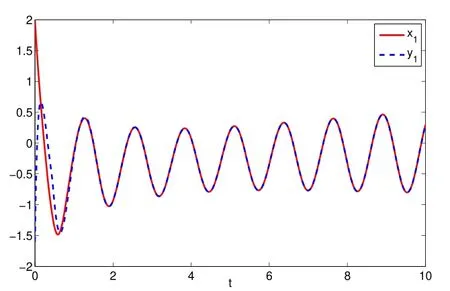
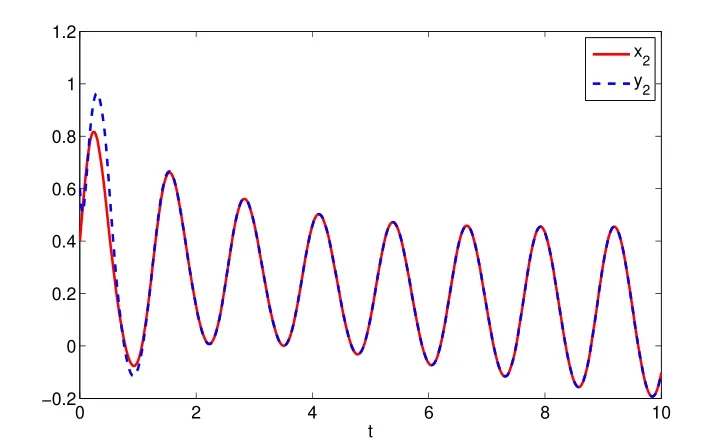
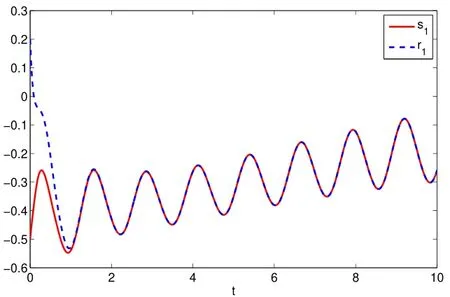
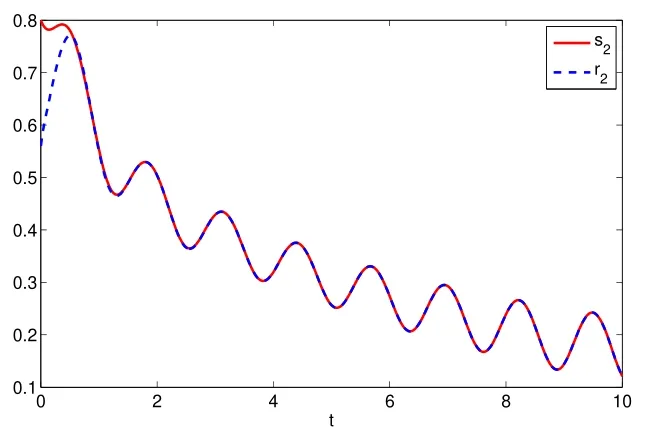
Assuming 2Time-lag τ Lemma 1[18]For any real matrix with proper dimension Σ1,Σ2,Σ3,if givenand any real number ε>0,then Lemma 2[13]IfP∈Rm×nis a positive definite matrix,Qis a symmetric matrix,then we have λmin(P−1Q)XTPX≤XTQX≤λmax(P−1Q)XTPX,X∈Rn. Lemma 3[17]Let ϕ is a nonnegative function in interval [t0−τ,+∞),and it is continuous in the subinterval [t0,+∞).Whent≥t0,ϕ′≤αϕ(t)+βϕ(t−τ)holds.If α>0,β>0,then,whent≥t0,we have ϕ(t)ϕ(θ),and η>0 is the unique solution of the equation α+βe−ητ=η. Lemma 4(Halanay inequality)[19]Let ϕ :[t0−τ) →[0,+∞) is a continuous function,whent≥t0,such that ϕ′≤−αϕ(t)+βϕt.If α>0,β>0,then,whent≥t0,we have ϕ(t)e−γ(t−t0),where ϕt=supt−τ≤θ≤tϕ(θ),and γ>0 is the unique solution of the equation α−γ−βeγτ=0. Lemma 5Suppose the functiony(t)is continuous and nonnegative int∈[−τ,+∞).If there are constants γ1,γ2,γ3,γ4the following conditions are met This contradicts with the inequality(10).So,the inequality(9)holds,i.e.,for anyt∈[δ,T), Then,for anyt∈[−τ,T),we have W(t) Next,we prove for anyt∈[T,T+δ),we have Otherwise,there existsp1∈[T,T+δ),such that This contradicts with the inequality(14).Hence,(13)holds. Fort∈[T+δ,2T),by the similar method,we get Repeating the above process,for anytk≤t≤sk,we have In addition,forkT+δ For anyt≥0,there exists a positive integerk,such thatkT≤t≤(k+1)T.So,for anyt,we have the following estimations for W(t).WhenkT≤t WhenkT+δ ≤t<(k+1)T,we have Remark 1In lemma 5,we only demand τ In this section,the strict derivation of the synchronization criterion for system (3) and system (4) is given based on differential inequality and intermittent control strategy. Theorem 1Under assumings 1,2,the system(3)and system(4)synchronize with intermittent control protocol,if there exists positive numbers α1,α2,εi,µi(i=1,…,4)and positive definite matricesQ1,Q2meeting the following conditions where γ and η are the solutions of equations α1−γ−β1eγτ=0 and α2+β2eητ=η respectively.Obviously,V(t)is an non-increasing function int∈(nT≤t≤nT+δ],but it is non-decreasing function int∈(nT+δ ≤t≤(n+1)T].V(t)att=nTandV(t)att=nT+δ.Since there is no special limit on the scale size of delay τ,it is possible thatnT−τ belongs to interval((n−1)T,(n−1)T+δ],or to interval((n−1)T+δ,nT].Similarly,it is also possible thatnT+δ−τ belongs to interval((n−1)T+δ,nT]or(nT,nT+δ].Therefore,the following proof process needs to be divided into two cases: Case 1:When δ−τ>0,we need to prove From assuming 2,there existsVτ≥V0. The following is proved by mathematical induction. (i)Whenl=0,i.e.,whent∈[0,T],by(18),we have Whenl=n,t∈(nT,(n+1)T],by(18),we have As long as the expressionsVnTandVnT+δare derived,the above inequality can be obtained.From lemma 4,we obtain Remark 2In [17],the authors only considered the case of τ <δ(small delay),and gave some intermittent control synchronization criteria.In the process of proving the theorem 1,according to the relationship between τ and δ,we mainly divide it into two parts to prove the conclusion of the theorem.For the case of τ<δ(small delay),we use lemma 3 and 4 to get the condition of synchronization.In the case of τ ≥δ,we can not get the relevant conclusion directly from lemma 3 and 4.Therefore,lemma 5 is given.According to lemma 5,we can directly obtain the criterion of synchronization.Obviously,the conclusion is more general than that in[17]. Remark 3In this paper,we choose the controllersu1(t)andu2(t)as linear batch controllers.In fact,there are similar results for nonlinear batch controllers.For example,we select And we only need to assume that the continuous functionQ(·)satisfies the following condition In particular,if there is no delay in the neuron transfer function of the model(3),then the model(3)degenerates to the following form Therefore,the system is described as follows whereg(e(t))=f(y(t))−f(x(t)). Corollary 1Under assumption 1,the system(27)and(28)are synchronized with the intermittent control protocol,if there exists positive numbers α1,α2,εi,µi(i=1,2,3)and positive definite matricesQ1,Q2meeting the following conditions ProofConstructing Lyapunov functionV(t)=eT(t)e(t)+zT(t)z(t),whent∈[nT,nT+δ),by the derivative ofV(t),we get SoV((n+1)T)≤For ∀t∈[nT,nT+δ),by the mathematical induction,we can obtain obviously Remark 4In this section,we require 0<δ Corollary 2Under assumings 1,2,the system(3)and system(4)are synchronized with the controller(32),if there exist positive numbers α1,εi(i=1,…,4)and positive definite matricesQ1,Q2meeting the following conditions Consider a numerical example of 2−Dcompetitive neural networks with variable time delay wherex(t)=(x1(t),x2(t))T,S(t)=(s1(t),s2(t))T,f(x)=(0.6tanh(x1)+0.4sin(x1),0.6tanh(x2)+0.4sin(x2))T,τ=0.4,C=0.8I,B=0.3I,ε=0.4, The initial conditions of this dynamic behavior system arex(0)=(2,0.4)T,S(0)=(−0.5,0.8)T,and the operation results are shown in Fig 1,Fig 2. Fig 1 the phase diagram of x(t) Fig 2 the phase diagram of S(t) Consider the synchronization between the main system(33)and the slave systems(34) wherey(t)=(y1(t),y2(t))T,R(t)=(r1(t),r2(t))T.The state with initial conditionsy(0)=(−1.6,0.6)T,R(0)=(0.2,0.56)T,xi(t),yi(t),si(t)andri(t)(i=1,2)have no control,as shown in Fig 3~Fig 6.Obviously,the trajectory of master-slave system is not synchronous without control. According to the analysis of theorem 1,the main system(33)and the slave system(34)tend to be synchronized under appropriate conditions after periodic intermittence control(5)and(6)are added to the system.For convenience,we chooseQ1=3.5I,Q1=3I,ε1=µ1=2,ε2=µ2=1,ε3=µ3=0.5,ε4=µ4=0.25.By simple calculation,it is found that the conditions(1)~(4)of theorem 1 hold.As long as we choose δ=2,T=3,the condition(5)(i)of theorem 1 holds.So,in this example,where δ=2,T=3,under the periodic intermittent control(5)and(6),track patterns ofxi(t),yi(t),si(t),andri(t)(i=1,2)are shown in Fig 7~Fig 10.Obviously,the master-slave system tends to be synchronized. Fig 3 the states of x1(t)and y1(t) Fig 4 the states of x2(t)and y2(t) Fig 5 the states of s1(t)and r1(t) Fig 6 the states of s2(t)and r2(t) Fig 7 the states of x1(t)and y1(t) Fig 8 the states of x2(t)and y2(t) Fig 9 the states of s1(t)and r1(t) Fig 10 the states of s2(t)and r2(t) This paper considers a competitive neural networks model with time-varying delay based on the neural networks with time-varying delay in which the intermittent feedback control with non-zero duration can be stabilized to continuous time.By using the method of differential inequality analysis and Lyapunov function,the global exponential synchronization conditions of competitive neural networks with time delay are discussed,and the corresponding criteria are established.At the same time,the exponential synchronization problems of competitive neural networks with time-varying delays and intermittent control are studied,and which satisfied both large and small delays.Some sufficient conditions are established.Finally,a simulation example is shown to verify the correctness and validity of the theoretical results.
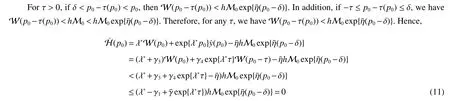
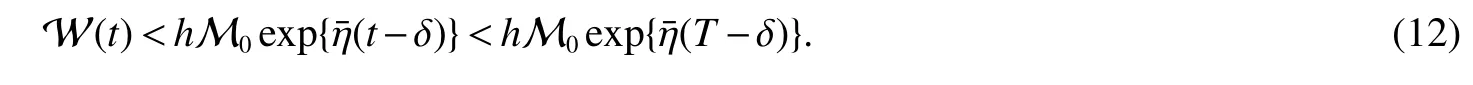

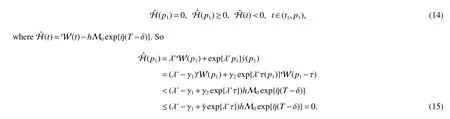
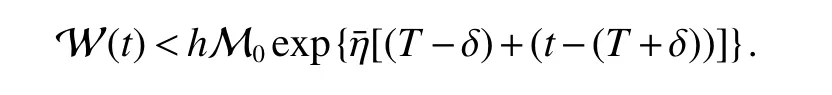

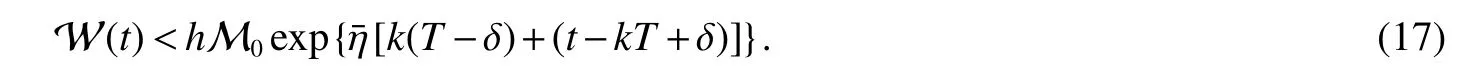
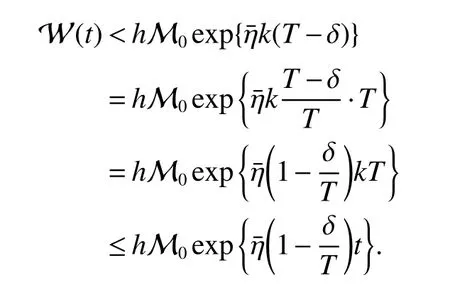
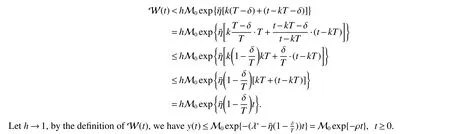
2 Synchronization criterion of competitive neural networks under intermittent control

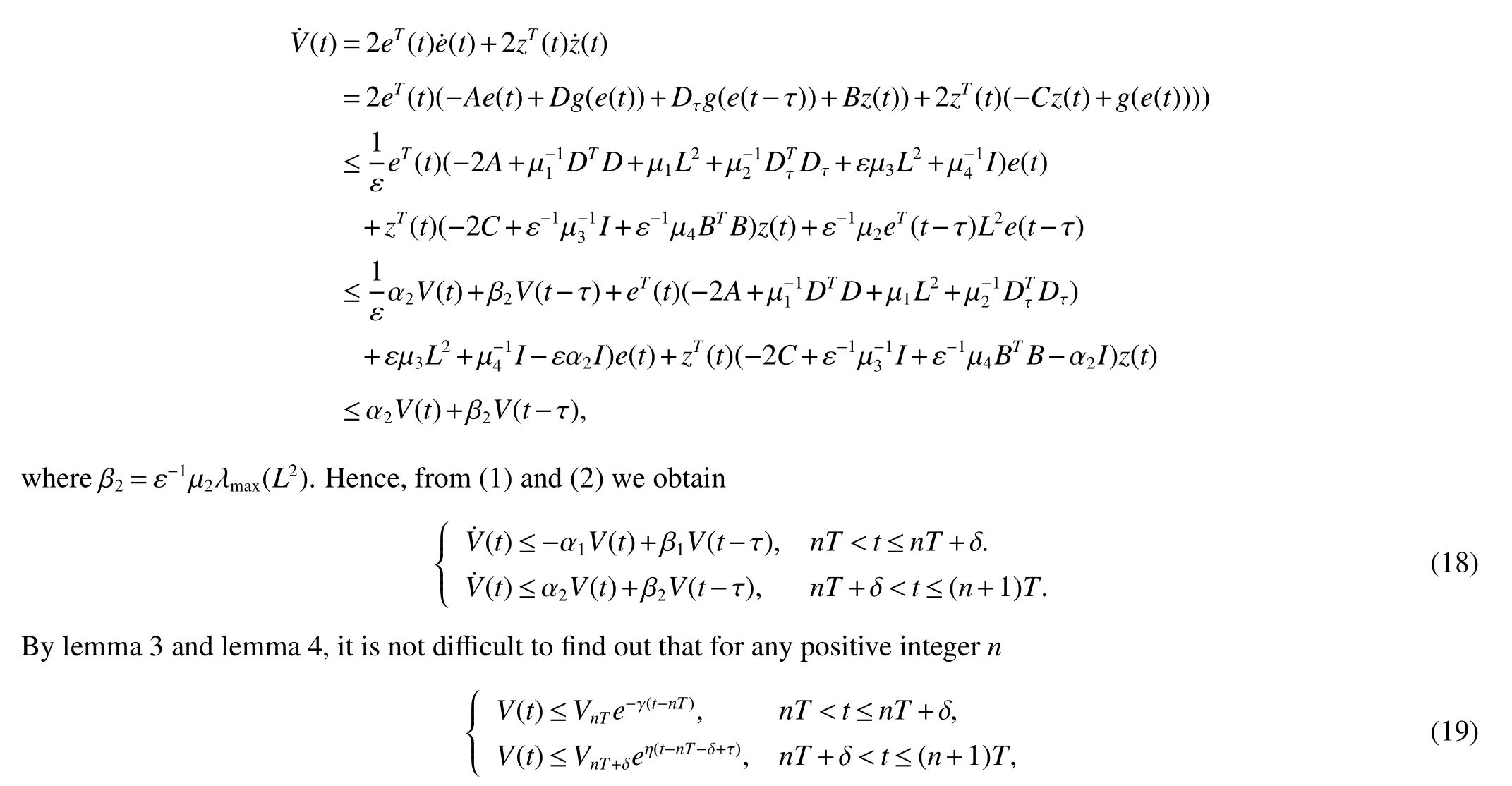
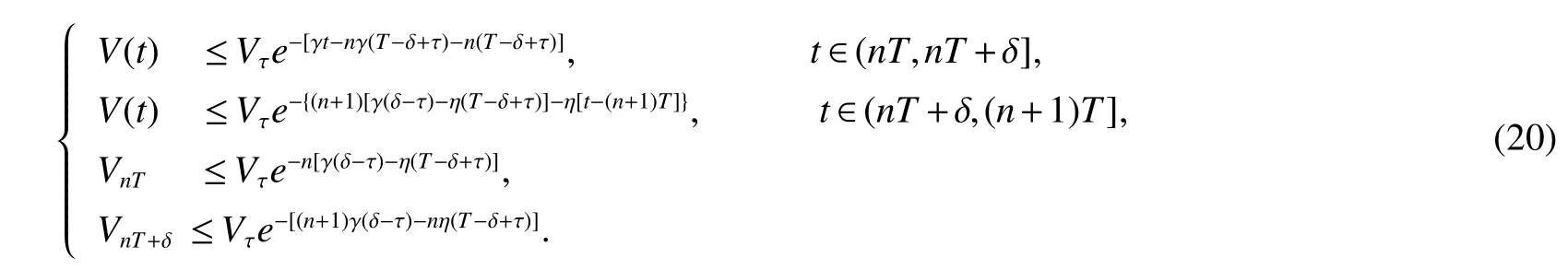

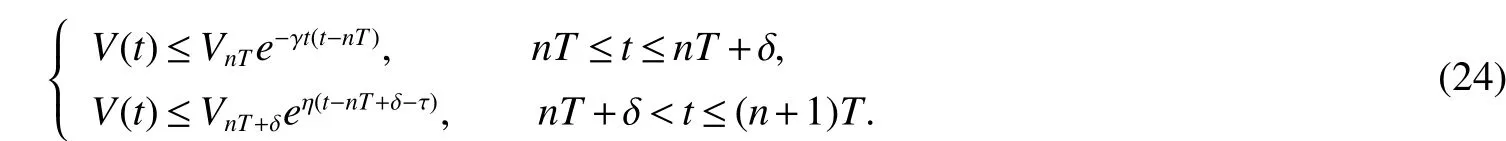

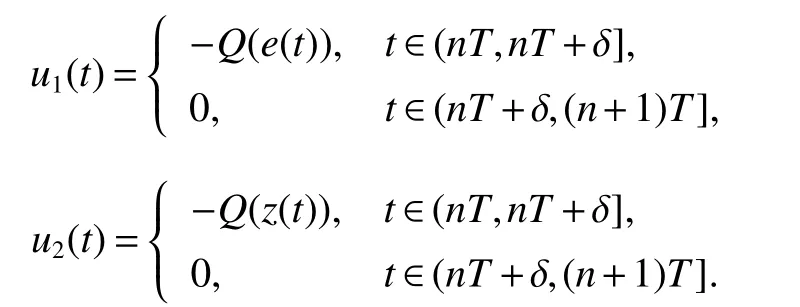
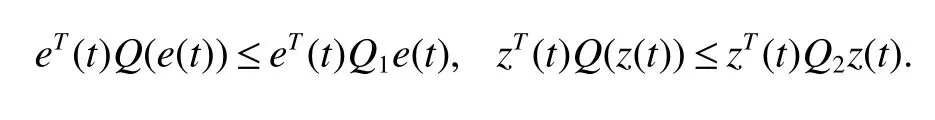
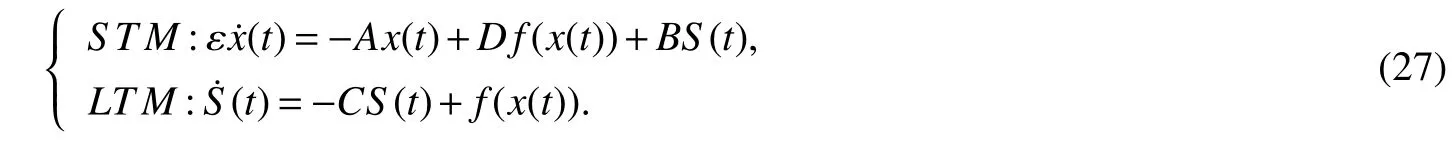

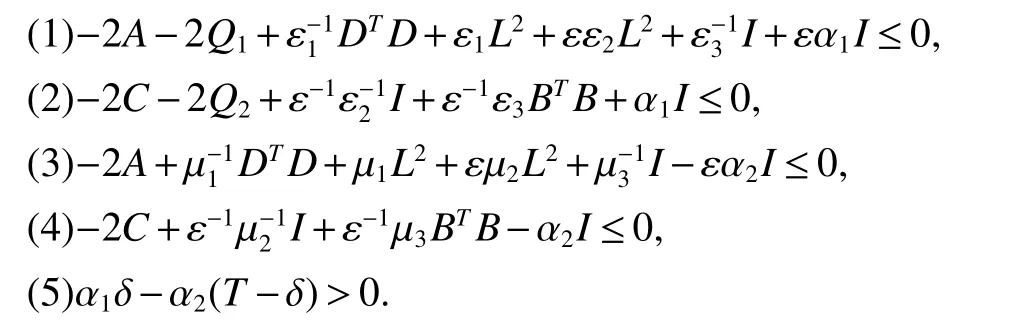
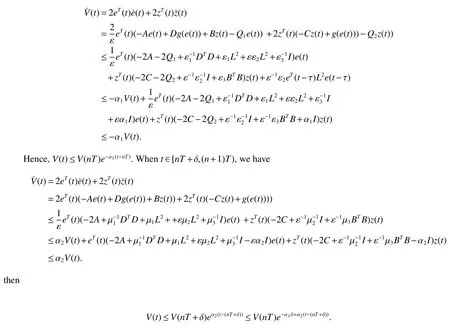
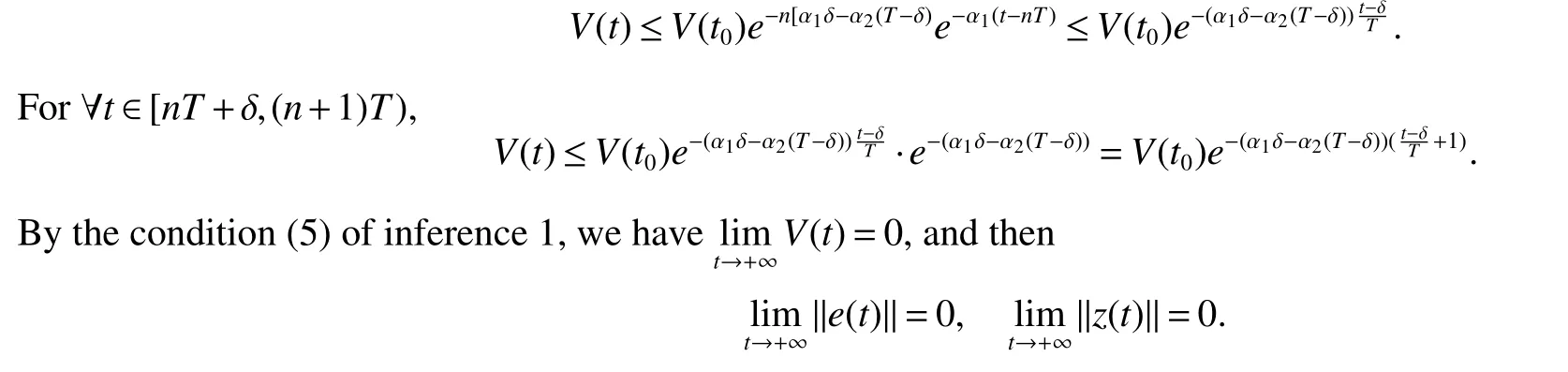

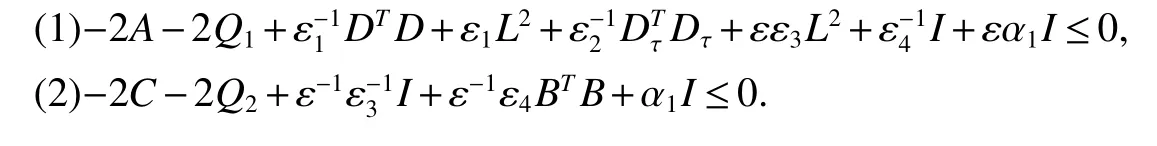
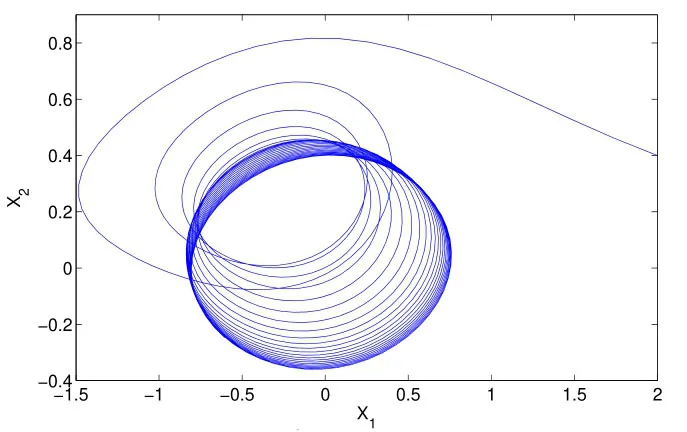
3 Numerical example and simulation
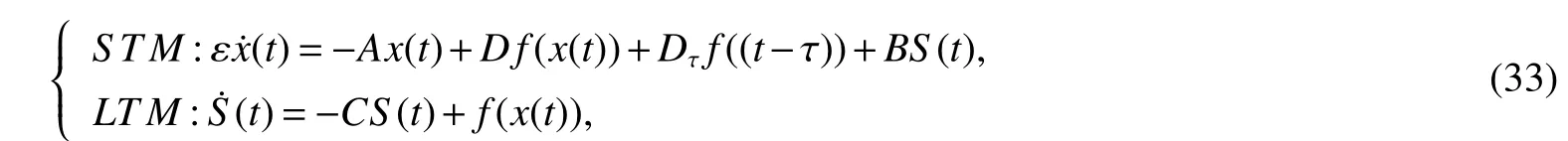
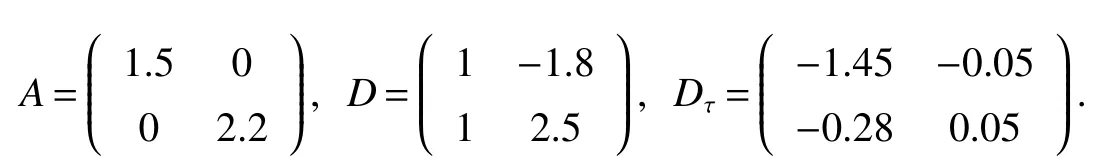
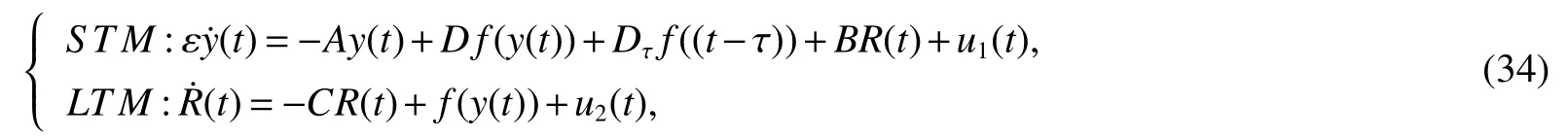
4 Conclution

