基于软粗糙模糊集的PROMETHEE决策方法
周 敏,牟 慧
(湖北民族大学 数学与统计学院,湖北 恩施 445000)
在现实生活中,不确定性问题普遍存在,如何更加有效地描述和提取隐藏在不确定数据中的有效信息,成为数学、计算科学以及相关领域的研究人员迫在眉睫需解决的一大难题.对此,他们提出了模糊集[1]、粗糙集[2]、软集理论[3]等.由于现实问题往往非常复杂,于是人们逐渐倾向于将这几种理论融合起来研究,提出了模糊粗糙集[4]、软粗糙集[5]、模糊软集[6]、粗糙模糊集[7]等.Feng等[8]将软集、模糊集和粗糙集相结合,提出了软粗糙模糊集的概念,并在此基础上研究了其相关性质,但它存在缺陷—它必须建立在满软集之上.为了解决这一问题,周敏[9]提出了一种新的软粗糙模糊集—M-软粗糙模糊集.
另一方面,多属性决策,尤其是伴随不确定性信息的多属性决策问题[10],已经成为现代生活众多应用领域中的重要问题.它是根据一定的准则或属性,在合理的时间内从所有可行的方案中寻找最优的方案.Brans等[11]提出的ROMETHEE决策法是一种常用的基于超越关系的一种方法,它通过对优先函数进行计算,然后利用净流量进行决策,从而得到各个选项中的部分排序和完全排序.随着不确定性理论的发展,许多学者逐渐将其融入不确定性决策问题之中,得到了一些较好的结论[12-13].付清等[14]基于文献[8]定义的软粗糙模糊集,给出了一种决策方法,并通过实例分析说明了该算法的可行性.然而,关于M-软粗糙模糊集在决策方面的应用研究还比较少.鉴于此,本文将PROMETHEE方法与M-软粗糙模糊集相融合,探究了它们在多属性决策中的应用,为解决具有不确定信息的多属性决策问题提供了一种新的研究思路.
1 预备知识
令A为初始论域,E为参数空间,是与U中有联系的所有参数的集合.普通情况下,参数涉及对象的属性、特征或性质等.称(U,E)为一个软论域.论域中的所有子集构成的类称为U的幂集,记为P(U).
定义1[1]设A是参数集E的一个子集,F:A→P(U)是一个集值映射,二元组G=(F,A)是论域U上的一个软集,称F为软集G的近似函数.
定义2[2]设U是一个初始论域,隶属函数μ:U→[0,1]称为U上的一个模糊集.对U中任意一元素x,隶属值μ(x)表示x属于模糊集μ的程度.U上所有的模糊集记为F(U).特别地,设f∈F(U),对U中的任意元x,如果f(x)≡1,则f记为f1;如果f(x)≡0,则记f为f0.
定义3[4]设U是对象集,R是U上的等价关系,由U产生的等价类之集记为:U/R={[x]R|x∈U},其中,[x]R={y|(x,y)∈R}.称U与R构成的整体(U,R)为近似空间.对于任意X⊆U,记为:
R-(X)=∪{[x]R|[x]R⊆X}={x|[x]R⊆X},
R-(X)=∪{[x]R|[x]R∩X≠φ}={x|[x]R∩X≠φ}.
分别称为X的下近似和上近似.若X的下近似和上近似相等,则称X是可定义的集合,否则称X为粗糙集.
定义4[8]设U是一个初始论域,(F,A)是U上的一个软集,定义一个从U到P(A)的集值映射如下:
φ:U→P(A),
x→{a|x∈F(a)}.

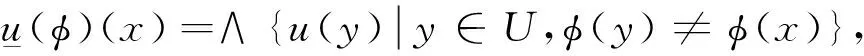
(1)
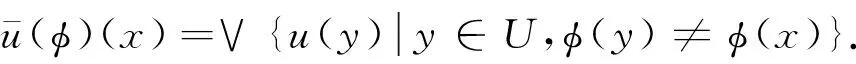
(2)

2 基于M-软粗糙模糊集的决策法
为了探究M-软粗糙模糊集在决策中的应用,本节以M-软粗糙模糊集为基础,提出了基于M-软粗糙模糊集的普通决策法和PROMETHEE决策方法.
2.1 基于M-软粗糙模糊集的普通决策方法
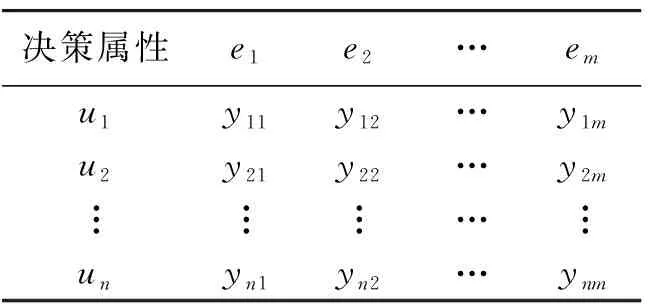
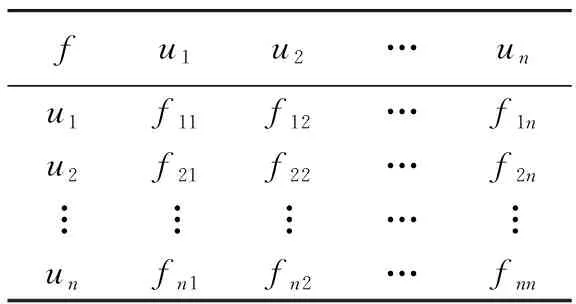
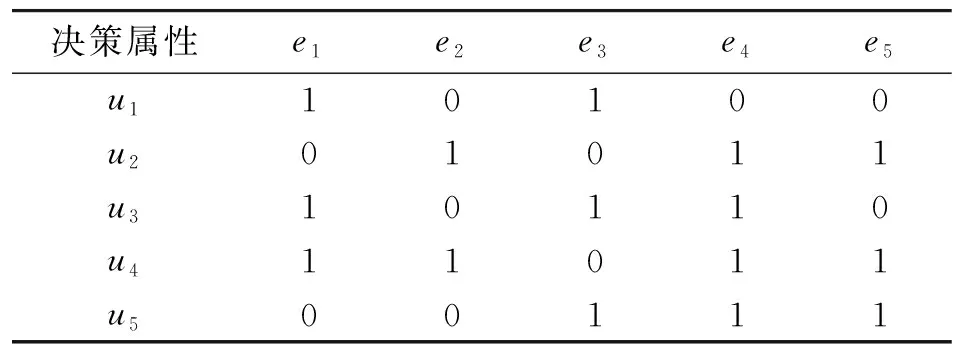
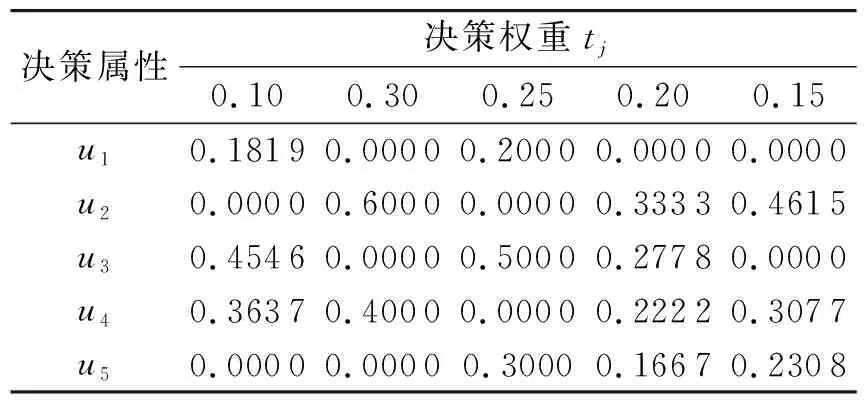
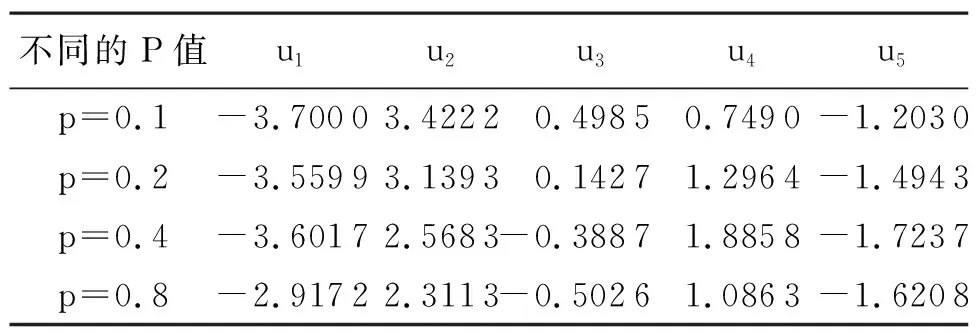
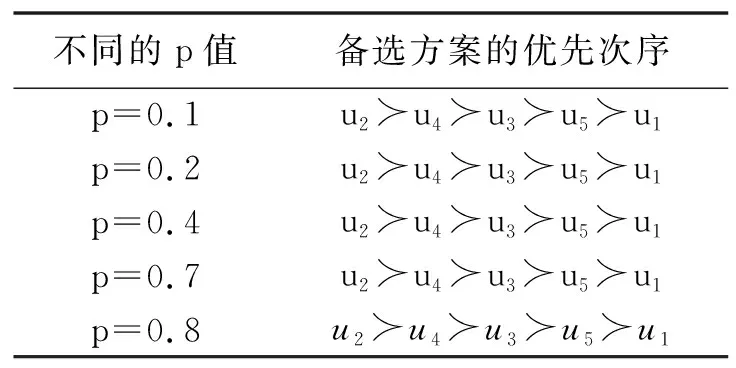
假设U={u1,u2,…,um}为一初始论域,E={e1,e2,…,el}为一参数集,其集合A={e1,e2,…,en}(n,l∈N,n 步骤1 输入软集(F,A),MS-近似空间(U,φ)中的映射和模糊集. 步骤3 计算选择值Hi(i=1,2,…,m): (3) 这里ui∈U. 步骤4 如果Hk=maxHi(i=1,2,…,|U|),则决策就是uk=U. 步骤5 如果k有一个以上的值,那么任何一个Uk可以选择. 步骤6 输出uk. 例1假设(F,A)是集合U={u1,u2,u3,u4,u5}上的软集合,其中U是考虑中的药品组.A={e1,e2,e3,e4,e5}一组参数集,其中ei(i=1,2,3,4,5)表示患者肺炎的症状,分别代表“咳嗽”“呕吐”“胸痛”“发热”“呼吸困难”,H医生考虑病人用药用软集(F,A)表示,如表1所示,其中(U,φ)是一个MS-近似空间. 表1 软集(F,A)的多属性决策表Tab.1 Multi-attribute decision of the soft set (F,A) 表2 软集(F,A)的多属性决策表Tab.2 Multi-attribute decision of the soft set (F,A) 表3 软集(F,A)的多属性决策的数据标准化Tab.3 The data standardization of multi-attribute decision of the soft set (F,A) 根据基于M-软粗糙模糊集的普通决策法进行计算,如下. 步骤1 由表1可得: F(e1)={u1,u3,u4},F(e2)={u2,u4},F(e3)={u1,u3,u5}, F(e4)={u2,u3,u4,u5},F(e2)={u2,u4,u5}. MS-近似空间(U,φ)的映射φ:U→P(A)为: φ(u1)={e1,e3},φ(u2)={e2,e4,e5},φ(u3)={e1,e3,e4}, φ(u4)={e1,e2,e4,e5},φ(u5)={e3,e4,e5}. H医生的同事根据自己的经验对这5种药品给出了评价,得到如下模糊集: (4) 步骤2 根据模糊集(4),式(1)和式(2)计算得到M-下、M-上软粗糙近似算子: 步骤3 根据式(3)计算可得选择值Hi(i=1,2,3,4,5). H1=H4=H5=0.044 4,H2=0.09,H3=0.057 1. 排序得:H2>H3>H1=H4=H5. 由步骤3可知,H医生根据该决策方法做出决策,选择最佳药品u2,无法在药品u1、u4和u5中做出选择. 注1由上面的计算结果,知基于软M-粗糙模糊集的普通决策方法排序结果处于同一等级的较多.当医生发现药品u2,u3紧缺无法为病人提供时无法做出决策.说明该算法过程考虑还不是很全面,为解决这一问题,本文试图探讨下面的决策方法. 优先顺序结构评估(PROMETHEE)法是常见的一种多属性决策方法.本节将PROMETHEE法和M-软粗糙模糊集相结合提出了一种新的决策方法,用于解决软粗糙模糊集的多属性群决策问题,并将本文的算法应用到实例中. 假设U={u1,u2,…,um}为一初始论域,E={e1,e2,…,el}为参数集,集合A={e1,e2,…,en}(n,l∈N,n 步骤1 通过软集(F,A)给定一个多属性决策表,得到表2. 步骤2 为了方便我们把决策矩阵中的数据利用式(5)进行标准化处理,得到表3. (5) 步骤3 按照文献[11]中的优先准则.首先确定p,在属性ej上定义优先函数. pj:[0,1]2→[0,1], (6) 这里k,i=1,2,…,n,j=1,2,…,m,p(p∈[0,1])称为严格优先阈值. 再通过优先函数和权重标准,可以计算优先指数f为: (7) 这里k,i=1,2,…,n,j=1,2,…,m.然后根据优先指数f的计算结果得到优先指标矩阵表4. 表4 优先指标矩阵Tab.4 The optimization index matrix 表5 Me的上下近似值Tab.5 The upper and lower approximation of Me 表6 Ng的上下近似值Tab.6 The upper and lower approximation of Ng 表7 正流量、负流量和净流量Tab.7 The positive,negativeand net flow 设M={M1,M2,…,Mn}是一组模糊优化负流量,N={N1,N2,…,Nn}是一组模糊优化正流量.这里: 为选项ue关于其他选项的模糊优化负流量; 为选项ug关于其他选项的模糊优化正流量. 步骤4 基于优先指标矩阵表4和式(1)和式(2),计算Me上、下近似算子,其中e=1,2,…,n.结果为表5. 这里: (8) (9) 然后再根据上面同样的计算方法,计算Ng上、下近似算子,其中g=1,2,…,n.结果为表6,这里: (10) (11) 步骤5 计算每个选项的正流量、负流量以及净流量结果为表7. (12) (13) 这里的|*|代表了*的基数. 净流量:φ(ui)=φ+(ui)-φ-(ui),(i=1,2,…,n). (14) 步骤6 根据φ(ui)的值,确定了所有选项的分级,并选择最好的一个方案. 为了探究基于软M-粗糙模糊集的PROMETHEE决策法在实际生活中的应用,下面通过这个例题来进行验证. 例2(续例1)假设(F,A)是集合U={u1,u2,u3,u4,u5}上的软集合,其中U是考虑中的药品组.A={e1,e2,e3,e4,e5}一组参数集,其中ei(i=1,2,3,4,5)表示患者肺炎的症状,分别代表“咳嗽”“呕吐”“胸痛”“发热”“呼吸困难”.H医生考虑病人用药用软集(F,A)表示,如表8所示,其中(U,φ)是一个MS-近似空间. 根据上面基于软粗糙模糊集的PROMETHEE决策法,得到如下步骤. 步骤1 通过软集(F,A)给定一个多属性决策表见表8. 表8 软集(F,A)的多属性决策表Tab.8 Multi-attribute decision of the soft set (F,A) 步骤2 为了方便把决策矩阵中的数据利用式(5)进行标准化处理,得到表9. 表9 软集(F,A)的多属性决策的数据标准化Tab.9 Data standardization of multi-attribute decision of the soft set (F,A) 步骤3 按照文献[24]中的优先标准,首先确定严格优先阈值p=0.7,利用式(6)计算在属性ej上定义优先函数pj(xkj-xij).通过优先函数和权重标准,根据式(7)可以计算优先指标f得到结果为表10. 表10 优先指标矩阵Tab.10 Optimization index matrix 步骤4 基于表10以及式(8)~(11)、式(1)和式(2),计算上下近似算子的值Me和Ng,结果为表11和12. 表11 Me的上下近似值Tab.11 The upper and lower approximation of Me 表12 Ng的上下近似值Tab.12 The upper and lower approximation of Ng 步骤5 利用式(12)~(14)计算每个选项的正流量、负流量以及净流量,结果为表13. 步骤6 根据表13中φ(ui)的值,确定了所有选项的分级,进行排序得到:u2≻u4≻u3≻u5≻u1. 表13 正流量、负流量和净流量Tab.13 The positive negative and net flow 故医生最先选择药品u2,最先排除药品u1. 为了更好地比较两种决策方法,下面给出两种决策法排序结果的直观图,如图1所示. 图1 两种决策方法的结果比较Fig.1 Comparison results of two decision-making methods 注2通过图1,不难发现:两种决策方法的最佳选项相同,这充分说明了这两种决策方法的可信性;普通决策法中处于同一等级的选项比较多,故区分度不高,而PROMETHEE决策法中没有处于同一等级的选项,所以PROMETHEE决策法决策信息更灵敏.故基于M-软粗糙模糊集的PROMETHEE决策法更具有效性和合理性. 在上面的决策方法中,严格优先阈值p是一个关键参数.接下来,将依次分析参数对排序结果的影响.将p进行变值,得到如下结果,如表14所示. 表14 不同阈值的净流量 在上面的案例中,讨论了p的5个不同的值,即p=0.1,0.2,0.4,0.7,0.8.根据p的不同值,最后得到相同的排序结果,如表15所示. 表15 敏感性分析 为了更好地比较严格优先阈值p变化对决策结果的影响,下面给出它们的排序结果的直观图,如图2所示. 图2 严格优先阈值p变化的结果比较Fig.2 Comparison results of the changing threshold of strict preference p 注3从图2可以看出,严格优先阈值p对排序结果没有影响.备选方案的优先次序始终为u2≻u4≻u3≻u5≻u1.最优的选择是u2,也就是第二种药品,最先排除的选择是u1,也就是第一种药品.这说明该决策方法具有一定的稳定性. 本文探究了M-软粗糙模糊集理论在多属性决策中的应用.提出了基于M-软粗糙模糊集的普通决策方法和PROMETHEE决策方法.通过案例分析,对比分析和敏感分析对所提方法的可行性、合理性和有效性进行了验证.在进行多属性决策的过程中,可以充分利用模糊集、粗糙集和软集的优点,从而使决策更加有效.较其他有关软集的决策方法而言,本决策方法可适用于非满软集的情况,适用范围更广.基于目前的研究,今后还可将本文在决策上的研究思路应用于其他不确定性信息系统,如犹豫模糊信息系统、直觉模糊信息系统和三支决策等.


2.2 基于软粗M-糙模糊集的PROMETHEE决策方法





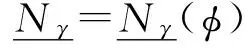
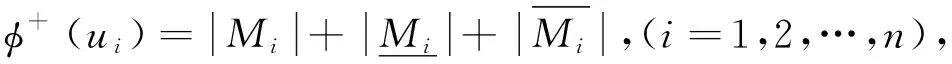

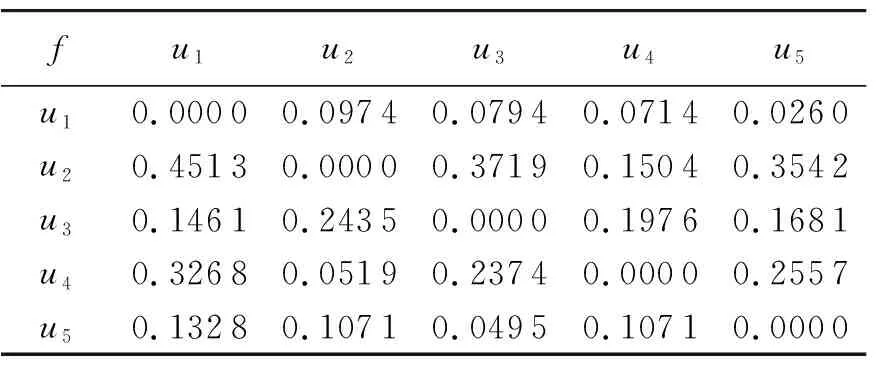

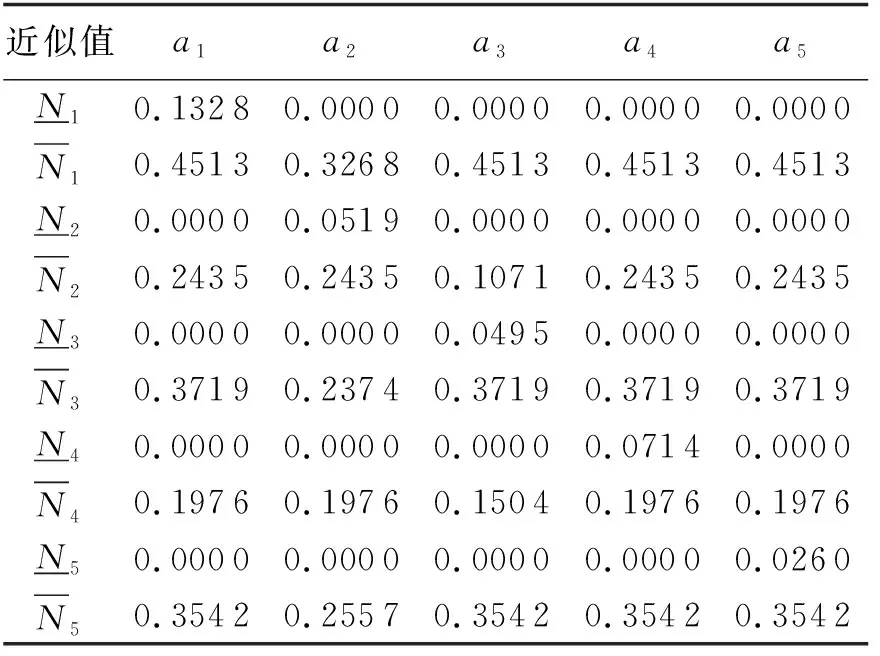
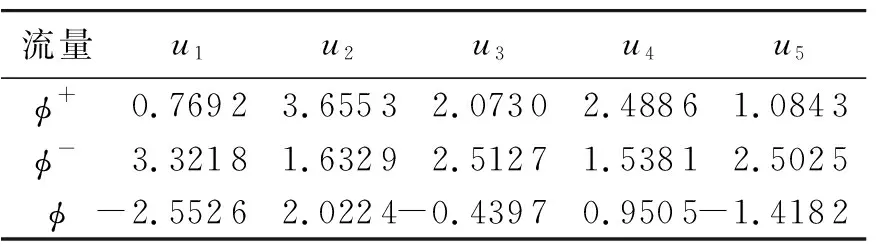
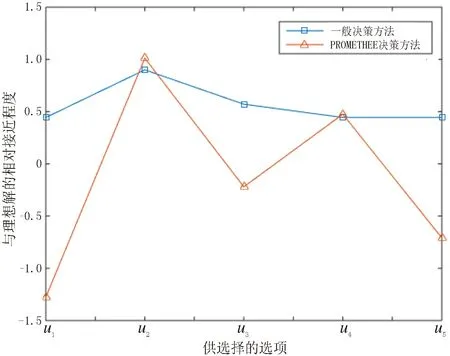
2.3 敏感性分析

3 结语

