不确定环境下救灾部队驻地选址及搜救路径优化

黄 茜， 王书勤， 邓少鸿， 范林军

(1.武警警官学院 基础部，四川 成都 610213； 2.武警警官学院 分队指挥系，四川 成都 610213； 3.长沙理工大学 经济与管理学院，湖南 长沙 410114； 4.武警警官学院 部队管理系，四川 成都 610213)

0 引言

抢险救灾中，灾区道路往往受到破坏，救灾分队行进时间不确定，受灾点所需救援时间也难以把握，不确定因素给部队救灾行动带来了较大困难。在资源有限、时间紧迫的情况下，科学地进行部队驻地选址、救灾任务分配，规划救灾分队搜救线路，实现救灾效果总体最优尤为重要。现有文献研究中地方应急物流系统中的LRP(location-routing problem)优化研究较多，但对不确定环境下救灾部队驻地选址及救援路径优化研究较少。郑斌等[1]以应急物资运达总时间最短和系统总成本最小为目标，建立了LRP优化模型；徐琴等[2]针对城市突发公共事件应急物流系统中的LRP，建立了一个应急救援时间满意度最大的LRP模型；Boyer等[3]提出一个关于工业危险废物的LRP双目标混合整数规划模型。基于此，本文考虑受灾点带时间窗，受灾点所需救灾时间与救灾分队行进时间均服从正态分布，救灾分队有有效救援时间约束等条件，建立了救灾总成本和总时间最短的LRP多目标随机规划模型，并设计改进遗传算法成功求解。

1 问题建模

1.1 问题的提出

抢险救灾中，在受灾点间的行进时间及其所需救援时间随机、各种资源有限的条件下，救灾部队如何根据受灾点信息选择驻地，确定救灾分队数量及其搜救路线。

1.2 模型假设

(1)有多个备选驻地，各驻地的建设费用已知。

(2)救灾分队数已知，救灾分队救灾效率、救灾固定成本和有效救灾时间相同，运输成本与运输距离成正比。

(3)每个受灾点只由一个救灾分队救援(若需多个将其分割)，救灾难度可用救灾时间衡量。

(4)每个救灾分队完成任务后返回原驻地。

(5)受灾点所需救灾时间及两受灾点间的行进时间均服从正态分布。

1.3 变量与符号说明

A={r|r=m+1,m+2,…,m+n}：受灾点集；

B={i|i=1,2,…,m}：备选驻地集；

S=A∪B：受灾点及备选驻地集；

V={k|k=1,2,…,K}：救灾分队集；

Fi：驻地i的建设成本；

c：救灾分队单位运输成本；

dij：i与j间的距离；

D：启用救灾分队的固定成本；

tij：i到j的时间，为正态分布随机变量；

T：救灾分队有效救灾时间；

tr：r点所需救灾时间，当r∈A，tr为正态分布随机变量，当r∈B，tr为0；

Tkr：救灾分队k到达点r的时间；

[0,LTr]：受灾点r的救灾时间窗；

M：足够大的正整数；

α1、α2：概率取值；

xi：0-1变量，备选驻地启用时为1，否则为0；

zik：0-1变量，备选驻地i的救灾分队k启用时为1，否则为0；

ykij：0-1变量，救灾分队k由i到j时为1，否则为0。

1.4 模型建立

根据以上思路，建立救灾问题中LRP多目标随机规划模型如下。

(1)

(2)

s.t.

(3)

p{0≤Tkr+tr≤TLr}≥α2,∀r∈A,∀k∈V；

(4)

(5)

ykij=0,∀i,j∈B,∀k∈V；

(6)

zik≤xi,∀i∈B,∀k∈V；

(7)

(8)

(9)

(10)

ykij(Tkj-Tki)≥0,∀i,j∈S,∀k∈V；

(11)

xi={0,1},∀i∈B；

(12)

ykij={0,1},∀i,j∈S,∀k∈V；

(13)

zik={0,1},∀i∈B,∀k∈V。

(14)

其中，式(1)为要求成本总和达到最小；式(2)为要求救灾总时间最短；式(3)表示救灾分队总救灾时间小于有效救灾时间的概率不小于α1；式(4)表示救灾分队救灾完成时间位于受灾点时间窗内的概率不小于α2；式(5)表示启用的备选驻地就有救灾分队进行救灾；式(6)表示救灾分队不在驻地间来往；式(7)表示启用的备选驻地才有救灾分队派出；式(8)表示救灾分队从被分到的驻地出发；式(9)表示救灾分队进入某受灾点，也从该点出去；式(10)表示受灾点只由一个救灾分队救灾；式(11)表示到达受灾点的时间具有先后顺序；式(12)、(13)、(14)为0-1变量约束[4]。

2 改进遗传算法设计

为求解模型，基于基本遗传算法，提出了一种改进遗传算法。与基本遗传算法相比，该算法主要在染色体编码、遗传操作设计及适应度函数的构造方面根据问题实际进行了针对性改进。在适应度函数上，基本遗传算法使用式(15)，而改进遗传算法使用式(16)：

f=z1+z2+z3+z4；

(15)

(16)

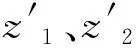
2.1 编码设计

染色体由3段基因组成，利用救灾分队、受灾点、备选驻地编号编码，具体编码方式如表1所示。

表1 染色体编码方式Table 1 Chromosome coding method

表1中，n为受灾点个数，K为救灾分队数量，m为备选驻地数，第1段由自然数1～K排列而成，第2段由自然数(m+1)～(m+n)排列而成，第3段由1～m中随机选择自然数排列而成。如：若K为4(1～4)，m为3个，n为6个(4～9)，则染色体244431-479856-2121表示1、2号备选驻地启用，2、4、3、1号救灾分队的搜救路线分别为2-4-2、1-7-9-8-1、2-5-2、1-6-1[6-7]。

2.2 适应度函数构造

(1)随机约束处理。利用罚函数思想，将模型中的随机约束处理如下。

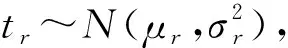
(17)

从而有

(18)

所以式(2)可以转化为

(19)

式中：Φ-1(α1)可由标准正态分布表查得。

由此可以构造罚函数：

(20)

式中：M1是一个足够大的数。

(21)

式中：L是分队k搜救线路上的点(驻点及受灾点)集，L′是线路上点r前的点集，M2是一个足够大的数。[8-9]

此时，目标函数可转化为

(22)

(2)适应度函数构造。改进遗传算法的适应度函数为f。

2.3 遗传操作的设计

求解过程中，采用了选择、交叉、变异3种遗传操作。

选择操作中主要采取精英法与轮盘赌法相结合的方法。用适应度函数的倒数构造轮盘赌法，每次依概率随机选择种群中的染色体；同时采用精英法，保留每次迭代的最好染色体，保证算法收敛。而基本遗传算法往往只采用轮盘赌法。

交叉操作分3个基因段进行，在选中的2个父代中分段随机选择2点k1、k2确定交叉点或匹配交叉基因串，然后再双点交叉与部分匹配交叉。若交叉后不合法，变更未参与交叉的基因使其合法，保存优秀染色体，具体操作如图1及图2所示。

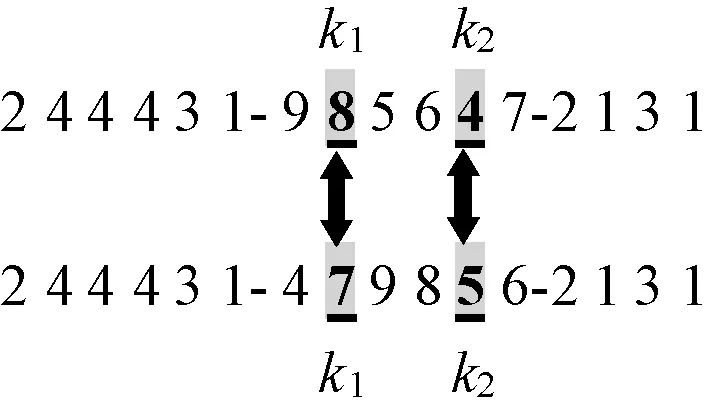
图1 双点交叉示意图Figure 1 Diagram of two points crossing

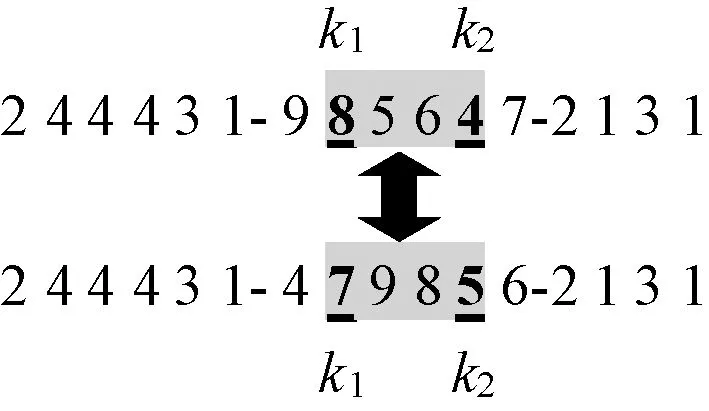
图2 部分匹配交叉示意图Figure 2 Diagram of partial matching crossing

变异操作在同一条染色体中分段进行，先随机选择2点，选址基因采用对换变异法，路径基因采用逆转变异法，具体操作如图3及图4所示[10-12]。

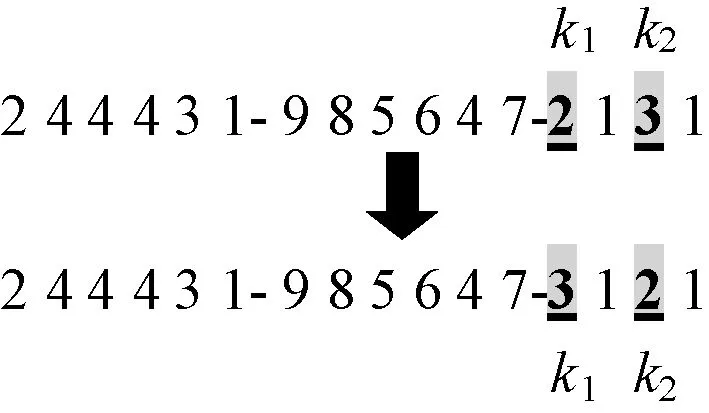
图3 选址基因对换变异法示意图Figure 3 Diagram of swap mutation

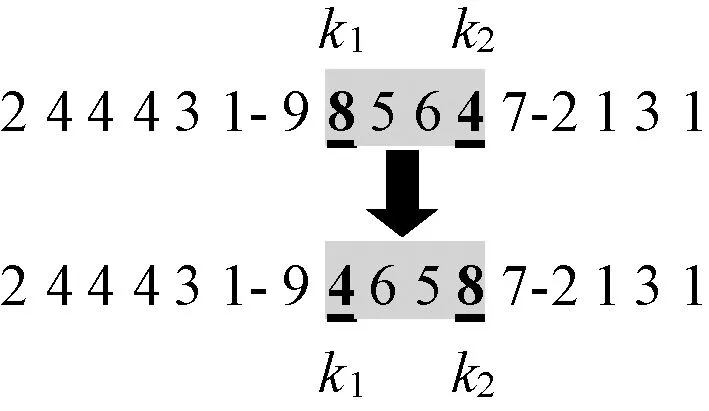
图4 路径基因逆转变异法示意图Figure 4 Diagram of reverse mutation

2.4 改进遗传算法流程

改进遗传算法设计流程如图5所示。

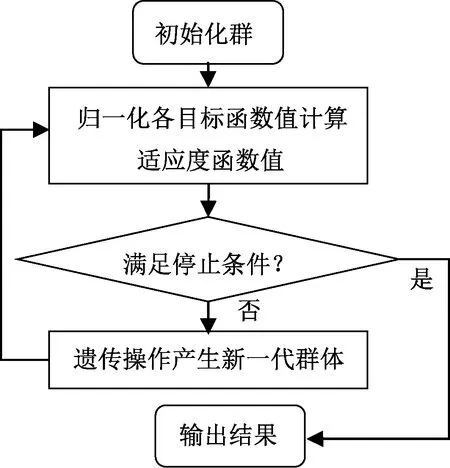
图5 改进遗传算法设计流程图Figure 5 Flow chart of the improved genetic algorithm

3 算例分析

3.1 算例陈述

某部队在抗震救灾中的救灾部队备选驻地坐标及建设成本如表2所示，受灾点信息如表3所示，受灾点间行进时间的均值和方差如表4和表5所示。救灾分队最大救灾时间为10 h，固定成本为0.5万元，单位运输成本为0.01万元，惩罚系数M1、M2均设为30，救灾分队到达受灾点的时间位于受灾点救灾时间窗的概率及救灾分队耗时位于最大有效救灾时间内的概率均为95%。

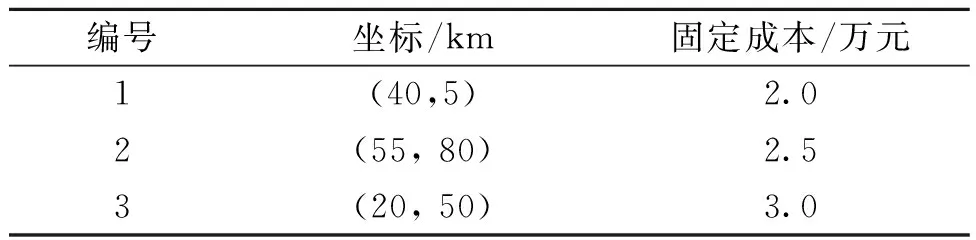
表2 救灾部队备选驻地数据Table 2 Data of alternative stations of earthquake relief troops

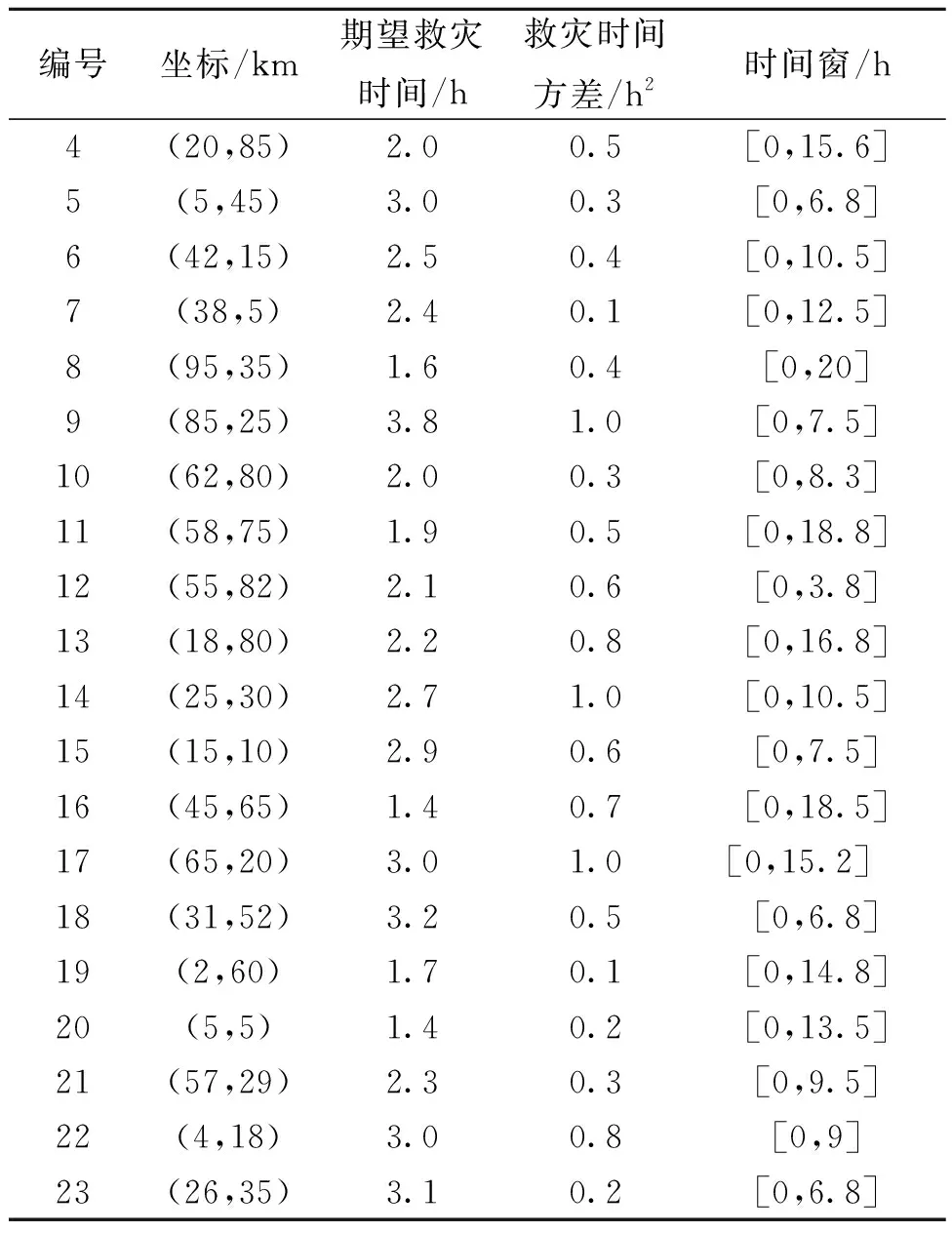
表3 受灾点数据Table 3 Data of disaster sites

3.2 改进遗传算法求解

在MATLAB中设置交叉概率pc=0.8，变异概率pm=0.35，置信度为0.95，最大迭代次数nc=50，种群规模popsize=50，计算耗时487.313 3 s，得到如下结果。

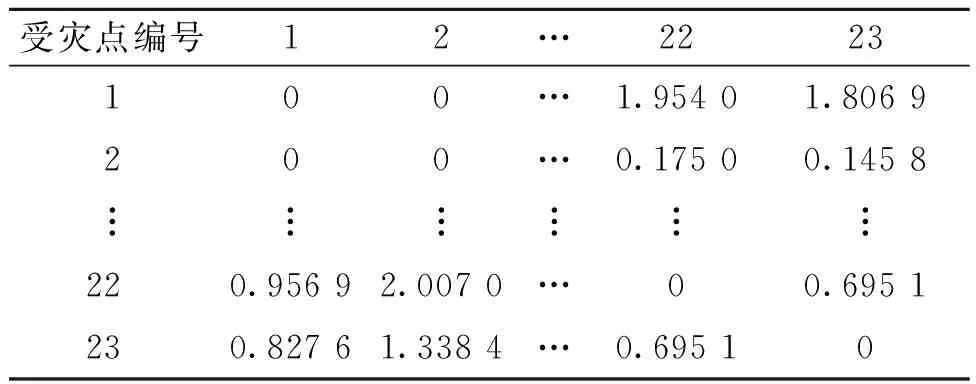
表4 部分受灾点间行驶期望时间/hTable 4 Expected travel time between some disaster sites

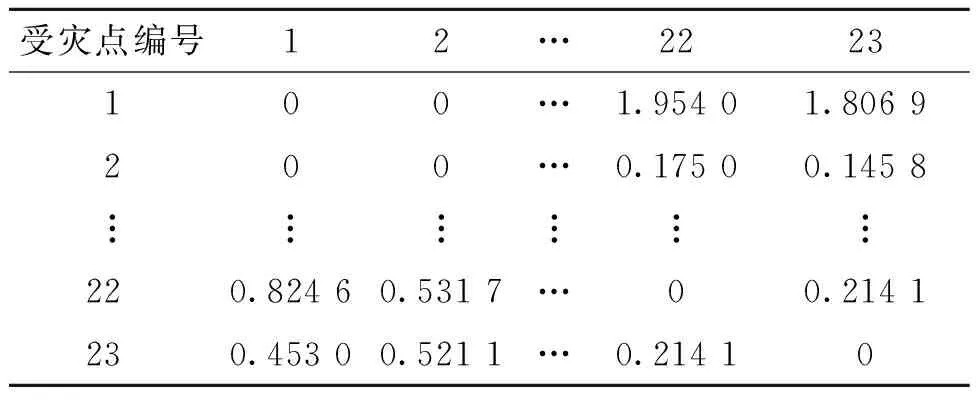
表5 部分受灾点间行驶时间方差/h2Table 5 Variance of travel time between some disaster sites

最优路径为3-21-18-3，3-19-5-3，1-22-15-1，1-6-1，1-17-7-20-1，3-14-23-3，3-10-11-16-3，3-12-3，1-8-9-1，3-4-13-3；费用成本为108.027 3万元；2种惩罚值为0；总救灾时间值为73.268 3 h；最小归一化目标函数值为7.715e-23。部队选择了1号和3号驻地，救灾任务分配给10个救灾分队，各分队均能在受灾点的时间窗内完成救灾，且不超过其最大有效救灾时间。

3.3 基本遗传算法及改进蚁群算法的求解

为检验改进遗传算法的优越性，本文同时利用基本遗传算法及文献[13]中的改进蚁群算法对问题进行求解，结果如表6及图6～9所示。

表6 本文算法与其他算法结果比较Table 6 Comparison results with other algorithms

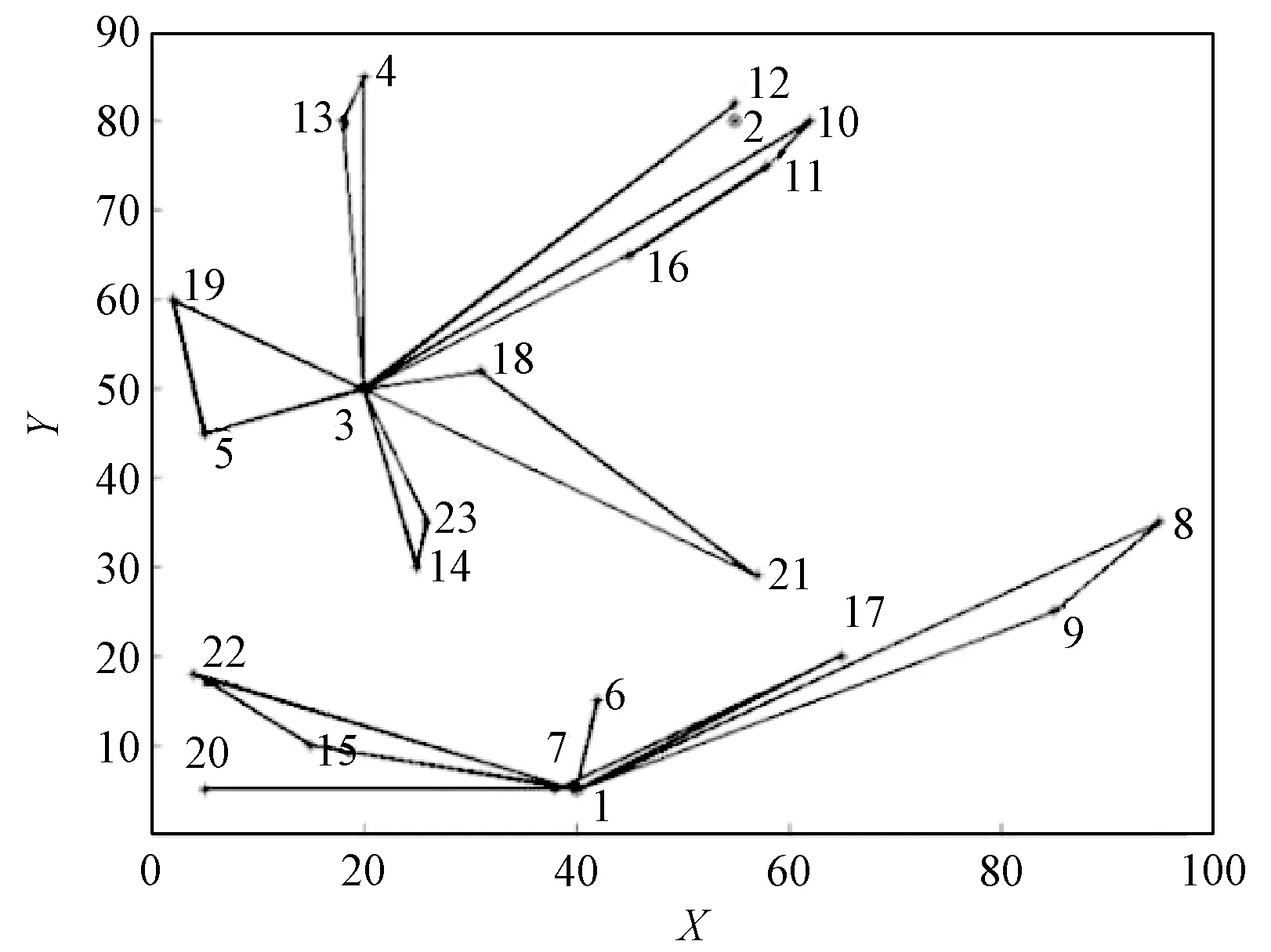
图6 改进遗传算法救灾分队搜救路径图Figure 6 Roads of disaster relief teams of the improved genetic algorithm

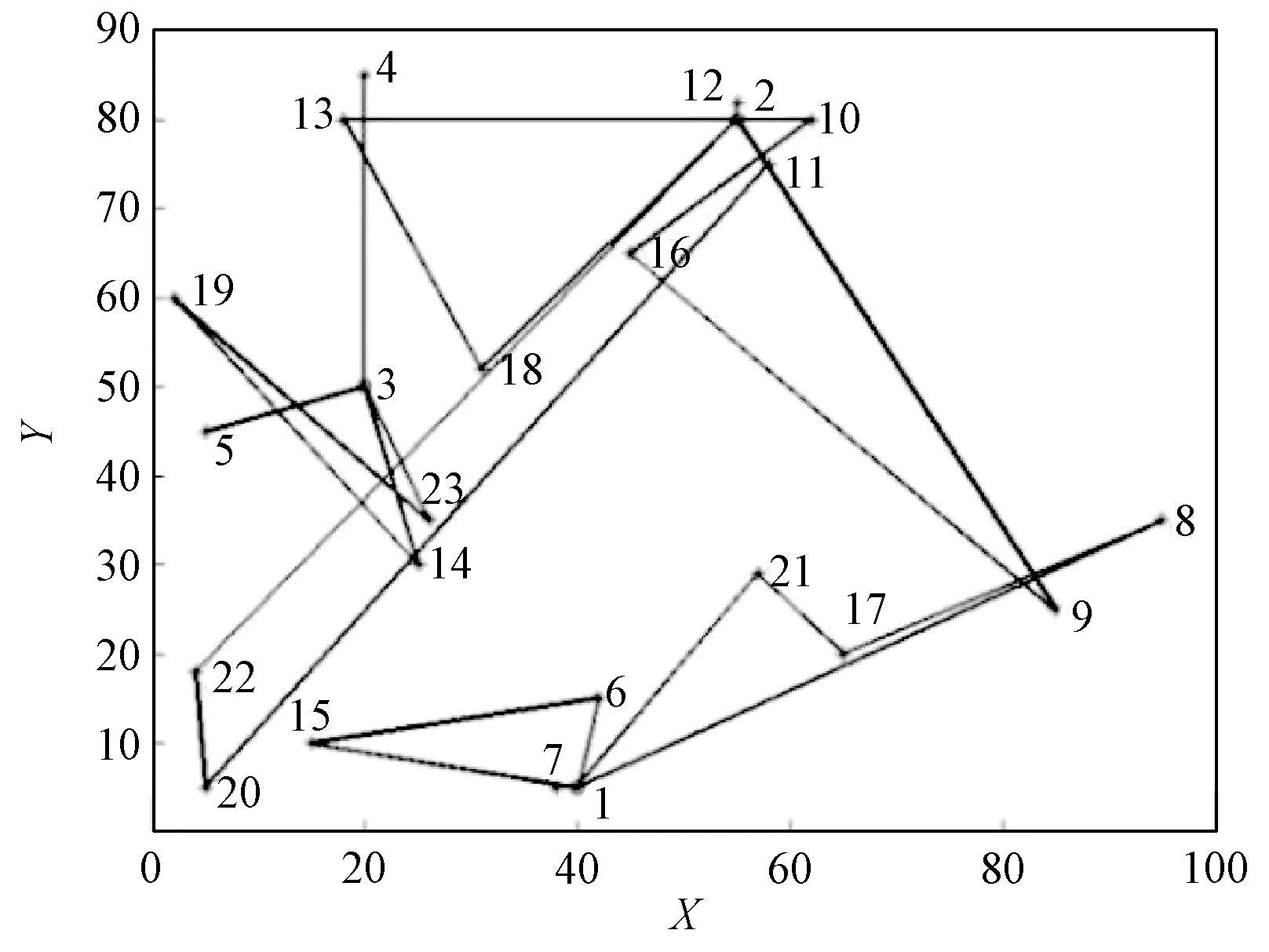
图7 基本遗传算法救灾分队搜救路径图Figure 7 Roads of disaster relief teams of the basic genetic algorithm

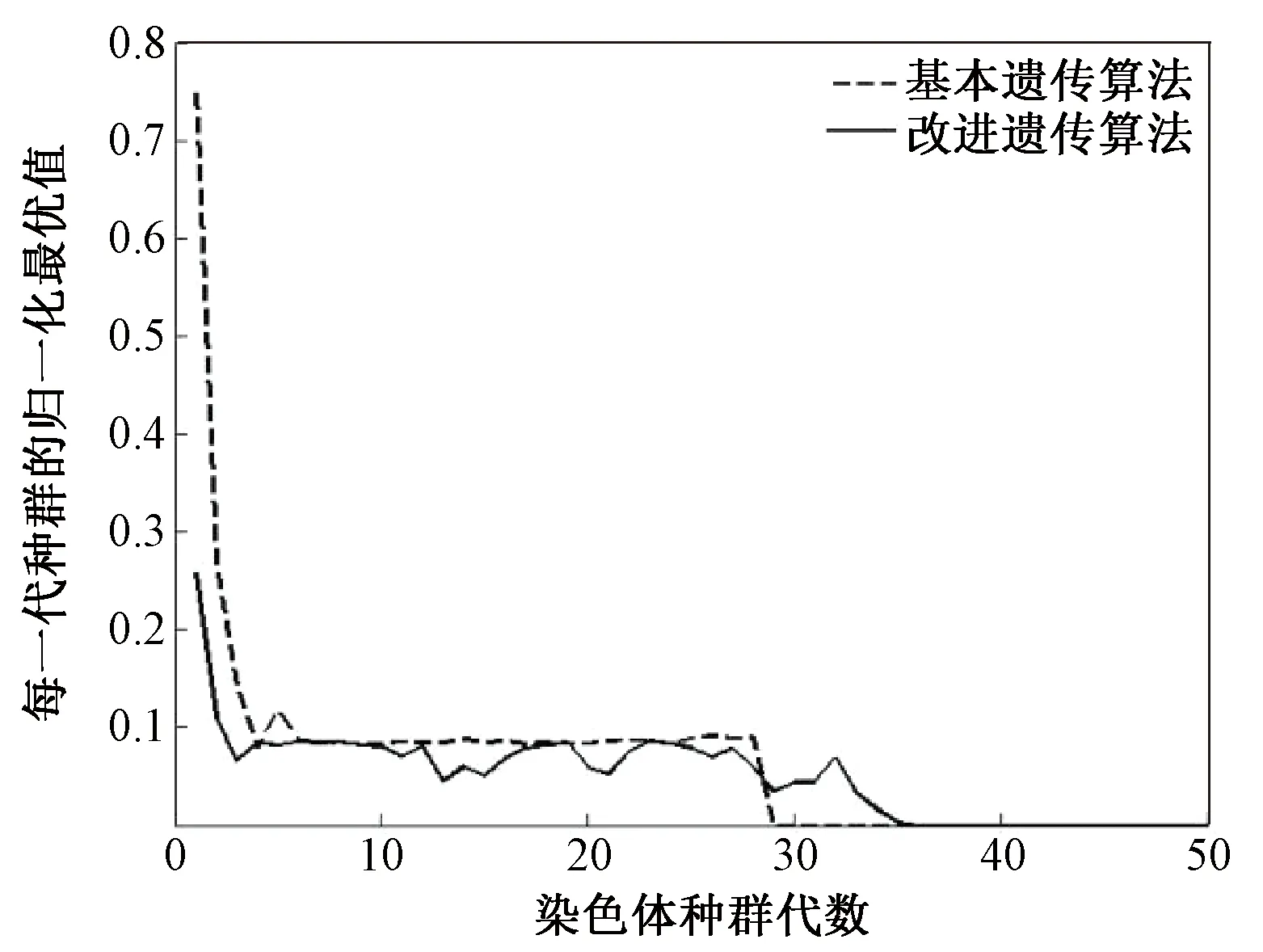
图8 2种遗传算法最优值进化图Figure 8 Evolution graph of optimal value of the two genetic algorithms

图9 改进蚁群算法救灾分队搜救路径图Figure 9 Roads of disaster relief teams of the improved ant colony algorithm

3.4 结果分析

由结果可知，改进遗传算法总救灾时间较短且惩罚值为0，而基本遗传算法的总救灾时间稍长，改进蚁群算法救灾总时间短，救灾费用成本低，但其2种惩罚值较大，难以完成救灾任务。综上所述，改进遗传算法与其他2种算法相比，具有较好的性能。

4 结论

本文分析了救灾环境中的不确定因素，建立了救灾部队驻地选址和救灾分队搜救路径问题的随机多目标规划模型，通过构造适应度函数、设计编码方法等手段，提出了一种改进遗传算法。实验结果表明，改进遗传算法能在稍微增加费用成本的前提下，实现惩罚值为0且救灾总时间较短(73.268 3 h)的优越综合性能。研究结果对抗震救灾行动组织具有一定的参考价值。