氯盐侵蚀钢筋混凝土框架结构可恢复性分析*
王 斌,苏 岸,杨 倩,徐菁津
(1.西安工业大学 建筑工程学院,西安 710021;2.西安建筑科技大学 西部绿色建筑国家重点实验室,西安 710055;3.中国电力工程顾问集团 西北电力设计院有限公司,西安 710075)
近海环境氯盐侵蚀下,钢筋混凝土(Reinforced Concrete,RC)框架结构发生中钢筋会出现锈蚀,使其承载力与抗震性能降低,从而导致震后结构损伤概率增加,结构的可恢复性进一步降低。在工程结构中提高建筑结构震后可恢复性以尽可能降低地震造成的经济损失和社会影响是研究人员一直探讨的核心问题[1-2]。因此,开展氯离子侵蚀下钢筋混凝土框架结构地震可恢复性分析对RC框架结构地震破坏的研究至关重要。
文献[3]将可恢复性这一概念引入到土木工程领域,并提出了一种定量评估和提高社区抗震可恢复性的方法。随着研究的进一步深入,可恢复这一概念在国外已被应用于社区,基础设施网络,以及单一建筑结构等不同层面上[4-5]。相比于国外,我国对于可恢复性的研究虽起步较晚,但成果显著[6-8],取得了关于RC框架结构可恢复性的评价体系[6];通过考虑结构所有损伤状态下的剩余抗震能力,实现了结构整体抗震可恢复性指数R的量化[7]。而在现有的结构地震可恢复性研究中,很少有考虑氯离子侵蚀对RC框架结构可恢复性的影响。因此,采用现有方法对受氯离子侵蚀的RC结构进行可恢复性评估,将会过高的估计受侵蚀RC结构的可恢复能力。
鉴于此,文中通过分析氯离子侵蚀下RC框架结构中钢筋劣化规律,得到RC框架结构时变损伤演化规律,在此基础上建立RC结构时变损伤地震模型,进而通过考虑恢复函数以及恢复时间,提出RC框架结构抗震时变可恢复性评估方法;通过实例分析,进一步说明文中所建结构可恢复性方法的实用性。
1 钢筋损伤模型
文献[9-10]给出了近海环境下氯盐侵蚀导致钢筋有效截面的减少是影响RC框架结构性能劣化的主要原因。为简化计算,目前大部分研究成果中仅考虑钢筋发生均匀锈蚀,基于以往均匀锈蚀下钢筋截面面积退化研究[11-14],考虑影响钢筋锈蚀各因素的模糊性,侵蚀后的钢筋直径D(t)可表示为
D(t)=D0-0.0232(t-t0)icorr(t)
(1)
其中,
(2)
式中:D0为钢筋的初始直径;icorr(t)为腐蚀电流密度;t为钢筋锈蚀时间;t0为钢筋初始锈蚀时间;w/c为水灰比;d为混凝土保护层厚度。
根据式(1)和式(2),得到基于时变腐蚀电流密度的锈蚀钢筋直径数学模型为
D(t)=D0-0.0232(t-t0)icorr
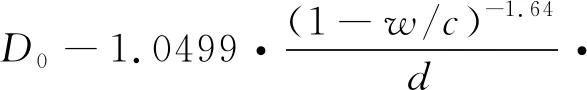
(t-t0)0.71
(3)
为了研究钢筋力学性能退化规律,以钢筋质量损失率δ(t)为基础进一步分析受侵蚀钢筋力学性能的劣化规律,其具体表达式为
(4)
目前,大多研究通过建立锈蚀后钢筋弹性模量,以考虑锈蚀对钢筋力学性能的影响。通过试验统计分析,得到了氯离子侵蚀环境下钢筋的弹性模量退化模型[15]为
当0<δ(t)≤5%时:
Es(t)=(1-0.052δ(t))Es0
(5)
当δ(t)>5%时:
Es(t)=(0.895-0.031δ(t))Es0
(6)
式中:Es0和Es(t)分别为钢筋锈蚀前和锈蚀后的弹性模量。
2 结构可恢复性分析
2.1 可恢复性分析
如图1(a)所示,现有结构功能可恢复性研究成果中大多忽略了外界环境的影响,即结构在t0E1时刻和t0E2时刻分别遭遇极端灾害时,结构的功能损失均下降ΔQ,同时,在一定的恢复时间内结构功能均可恢复到原有的功能水平。而处于氯离子侵蚀环境中的钢筋混凝土结构,其结构中的钢筋随着侵蚀时间不断锈蚀,结构构件各项力学性能亦随着侵蚀时间的增加而不断降低。因此,结构功能随着侵蚀时间不断衰退。如图1(b)所示,随着侵蚀时间的增加结构功能指数逐渐降低。当结构在t0E1时刻遭遇突发灾害时,结构功能降低ΔQ1,经过一定时间的恢复后,其功能指标Q(t)虽有恢复,但已达不到原有结构的功能。恢复后的结构仍继续受到氯离子侵蚀,其功能仍随时间不断劣化,当结构在t0E2时再次遭遇突发性灾害,结构功能指标函数在按照氯离子侵蚀衰退的轨迹上损失ΔQ2,经过一定时间的恢复后,其功能指标Q(t)恢复到按照原来氯离子侵蚀衰退的轨迹上,而无法恢复到原有结构功能。

图1 结构功能恢复路径
2.2 评估框架
基于文献[3]提出的可恢复力评估方法,文中考虑氯离子侵蚀的影响,对于退化RC框架结构的时变功能指标,可通过地震事件发生时间t0E到时间t0E+Trec之间的功能曲线下的归一化面积计算结构的恢复性能力,地震可恢复性如图2所示,可恢复性的指数见式(7)。

图2 退化结构地震可恢复性
(7)
式中:R为结构可恢复指数;Trec为地震事件恢复受损框架结构功能所需的时间;t0E为地震灾害发生时间。Q(t)为功能指标函数[16]通过计算得到:
Q(t)=1-{L(k,Trec)×[H(t-t0E)-
H(t-(t0E+Trec)]}frec(t,t0E,Trec)
(8)
式中:L(k,Trec)为损失函数;H(·)为阶跃函数;frec(t)为关于时间t的恢复函数。
由式(8)可以看出,结构在地震作用下恢复力的大小是由结构的损失函数L(k,Trec)和恢复时间Trec和恢复函数frec(t)的形状来决定。
2.2.1 损失函数
损失函数即结构在地震作用下的损伤程度。考虑所有影响结构损失的参数,可将结构在地震作用下的损失分为直接损失LD和间接损失LI。其中直接损失LD主要与受损结构灾后修复相关费用有关,通过某一损伤状态下的结构损伤概率乘以对应于该损伤状态的损伤率来计算。
对于受氯离子侵蚀的RC结构,其结构的抗震性能随着侵蚀时间的不断增加而不断退化。研究表明,RC框架结构损伤指数P可通过用于评价结构剩余抗震能力的峰值地面加速度(Peak Ground Acceleration,PGA)ag表示,对于考虑氯离子侵蚀影响的RC框架结构地震损伤可表示为
(9)
其中,
ag(t)=Ke(t)Δ(t)/m
(10)
式中:P(t)为钢筋锈蚀t时刻结构的地震损伤指数;ag(t)为钢筋锈蚀t时刻结构剩余抗震能力;ag,0为钢筋未锈蚀时结构剩余抗震能力;m为框架结构质量;Δ(t)为t时刻框架结构顶点位移;Ke(t)为钢筋锈蚀t时刻结构的有效刚度。
由于结构在侵蚀环境下随时间变化钢筋有效面积和弹性模量都会随时间发生变化,因此结构等效刚度Ke(t)可以表示为
Ke(t)=[Ec+ρs(t)Es(t)]·I
(11)
式中:Ec为混凝土弹性模量;ρs(t)为t时刻结构配筋率;Es(t)为钢筋混凝土时变弹性模量,可以根据式(5)和式(6)求得;I为截面惯性矩。
通过式(10)可计算出氯离子侵蚀下RC框结构的地震损伤指数,可进一步根据文献[17]给出的结构损伤指数范围定义结构的损伤状态,见表1。

表1 损伤状态与损伤指数
间接损失LI主要是指遭遇突发性灾害后造成的营业中断、收入损失和搬迁费用等,其估算需要考虑建筑结构事件前和事件后的使用信息。
直接损失LD和间接损失LI的分别为
(12)
(13)
式中:CO为结构某一损伤状态下维修成本与建筑结构重建成本的比值;Cop为某一损伤状态下运营成本增加部分与建筑结构重建成本的比值;CA为某一损伤状态下营业中断的经济损失与建筑结构重建成本的比值;PE(DS=k)为给定地震强度下结构处于损伤状态(Damage State,DS)k的概率。
损失函数L(k,Trec)可以通过直接损失LD和间接损失LI直接相加进行计算,表达式为
L(k,Trec)=LD+LI
(14)
2.2.2 恢复函数
恢复函数是结构功能指标函数的一个组成部分,主要是指地震后结构功能指标函数恢复到目标水平时结构性能的恢复,主要因素是结构的损伤程度和恢复率。结构的损伤程度关系到结构的鲁棒性和冗余性,结构功能的恢复率关系到抗震救灾决策者的重视程度。根据结构破坏程度和不同应急措施的速度,文献[18]研究发现Sigmoid函数最适合作为氯离子侵蚀下的结构功能恢复函数,其数学表达式为
(15)
式中:a为恢复曲线的迅速性;b为控制延x轴的弯曲。使用Sigmoidal函数的另一个优点是结构恢复模型的功能是考虑应激反应Qa的时间作为功能的一部分。如图3所示,结构在t0E时刻遭遇地震作用,功能指标损失,在结构经历一段空闲时间,即应急反应时间后,结构根据恢复路径进行恢复,并达到目标功能Qa。

图3 Sigmoidal函数
文献[19]认为应急反应时间与结构损坏程度有关,假设应急反应时间是均匀分布的,除轻微破坏外的任何结构损坏状态,应急反应时间可取为Trec的十分之一。根据Trec和实际恢复曲线的各自值计算参数a和b,得出四种结构损伤状态制定损伤状态特定恢复曲线,如图4所示。

图4 不同损伤状态下的恢复模型
3 算例分析
3.1 结构设计与建模
按照我国目前现有的《建筑抗震设计规范》和《混凝土结构设计规范》中的相关执行标准,考虑抗震设防烈度为8度,抗震等级为二级,II类场地条件,设计地震分组为第一组,设计一栋3层的钢筋混凝土框架结构,其中,底层层高为4 m,其余两层层高为3 m,楼面恒载均为4.5 kN·m-2,活载为2.0 kN·m-2,地面粗糙度为B类,结构的平面及立面布置(单位:mm)如图5所示,经过计算得到构件截面及配筋如图6所示。
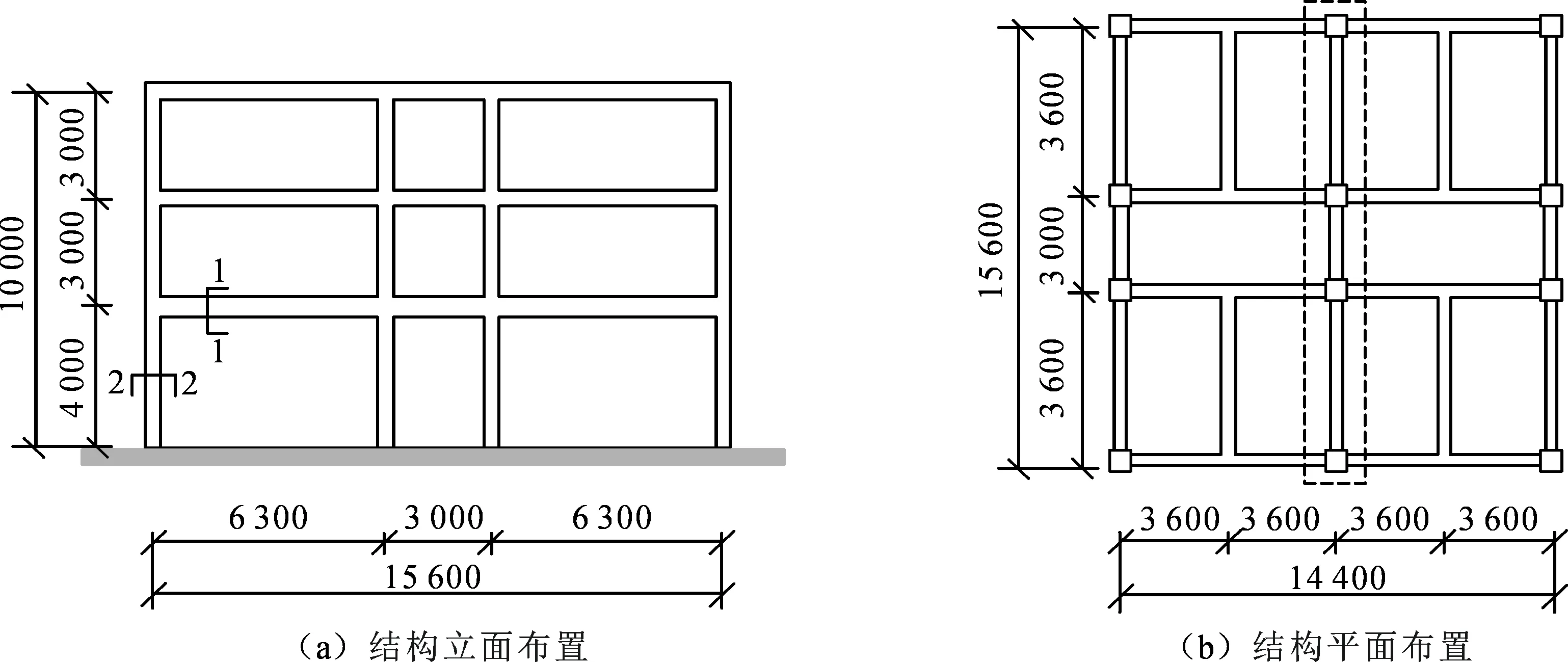
图5 框架结构模型图
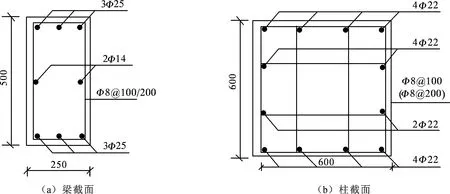
图6 截面配筋图
本文采用OPENSEES软件平台进行建模与分析[20-22]。在RC框架结构的建模过程中,混凝土采用Concrete02本构模型,并考虑箍筋对核心区混凝土约束,钢筋采用Steel02本构模型。梁柱单元模型均采用纤维单元模型。
3.2 结构易损性分析
选取22条经典地震波作为框架地震易损性分析的输入地震动,对结构进行不同地震波多次调幅后的非线性动力时程分析,获得不同损伤状态下,基于时变的钢筋混凝土框架结构易损性曲线,如图7所示。

图7 RC框架结构不同损伤状态的易损性曲线
从图7可以看出,在不同损伤状态的超越概率中,遭遇同一地震峰值加速度下,同一服役时间内框架结构轻微破坏超概率最大。框架结构在服役前几年时,严重破坏和完全破坏的超越概率远小于轻微破坏和中等破坏,随着使用时间的推移,钢筋混凝土结构受氯离子侵蚀影响较长,使用40~50年时,严重破坏和完全破坏的超越概率与轻微破坏和中等破坏的超越概率间的差别明显缩小。随着PGA的增加,同一服役时间结构中各破坏状态的超越概率逐渐增大。同时为进一步反应对氯离子侵蚀对结构易损性的影响,图8给出了受氯离子侵蚀不同服役时间(0,10,20,30,40,50年)的结构地震易损性曲线。
从图8可看出,在氯离子侵蚀环境的影响下,当钢筋混凝土结构在不同服役时间遭遇同一地震强度时,其同一破坏程度的超越概率具有显著的增加,因此在氯离子侵蚀下,RC结构的抗震性能随着服役时间的增加而不断劣化。例如:当PGA=0.3 g时,框架结构在不同服役时间下的轻微破坏超越概率分别为38.35%,53.04%,64.87%,79.57%,89.96%,97.133%。

图8 不同服役时间下时变地震易损性分析
3.3 结构可恢复性分析
从易损性曲线中获得结构在不同损伤状态下的超越概率,建筑破坏引起的损失可依据结构损伤状态及类型在《地震现场工作第4部分:灾害直接损失评估》[23]给出的范围中选取适当的值,按照上述公式计算不同损伤产生的损失,并得到结构的损失率。图9给出了氯离子侵蚀不同服役时间的结构在地震动作用下的损失率变化情况。可以看出,随着结构劣化程度的不断提高,遭遇一定PGA的结构损失率增加速度更大,损耗比线性增加到0.6左右;超过此值后,损耗率随PGA的增加而降低,呈现非线性趋势。这主要是因为结构在使用前期氯离子侵蚀未造成钢筋锈蚀,因此对结构抗震性能的影响并不显著;当氯离子侵蚀造成钢筋锈蚀时,钢筋的有效截面受到削弱,结构的抗震性能会出现明显的退化。随着结构劣化程度的增加,在结构具有较高的破坏状态(即严重损伤和倒塌)时,此时对应的损失率明显增加,呈现出明显的非线性变化趋势。
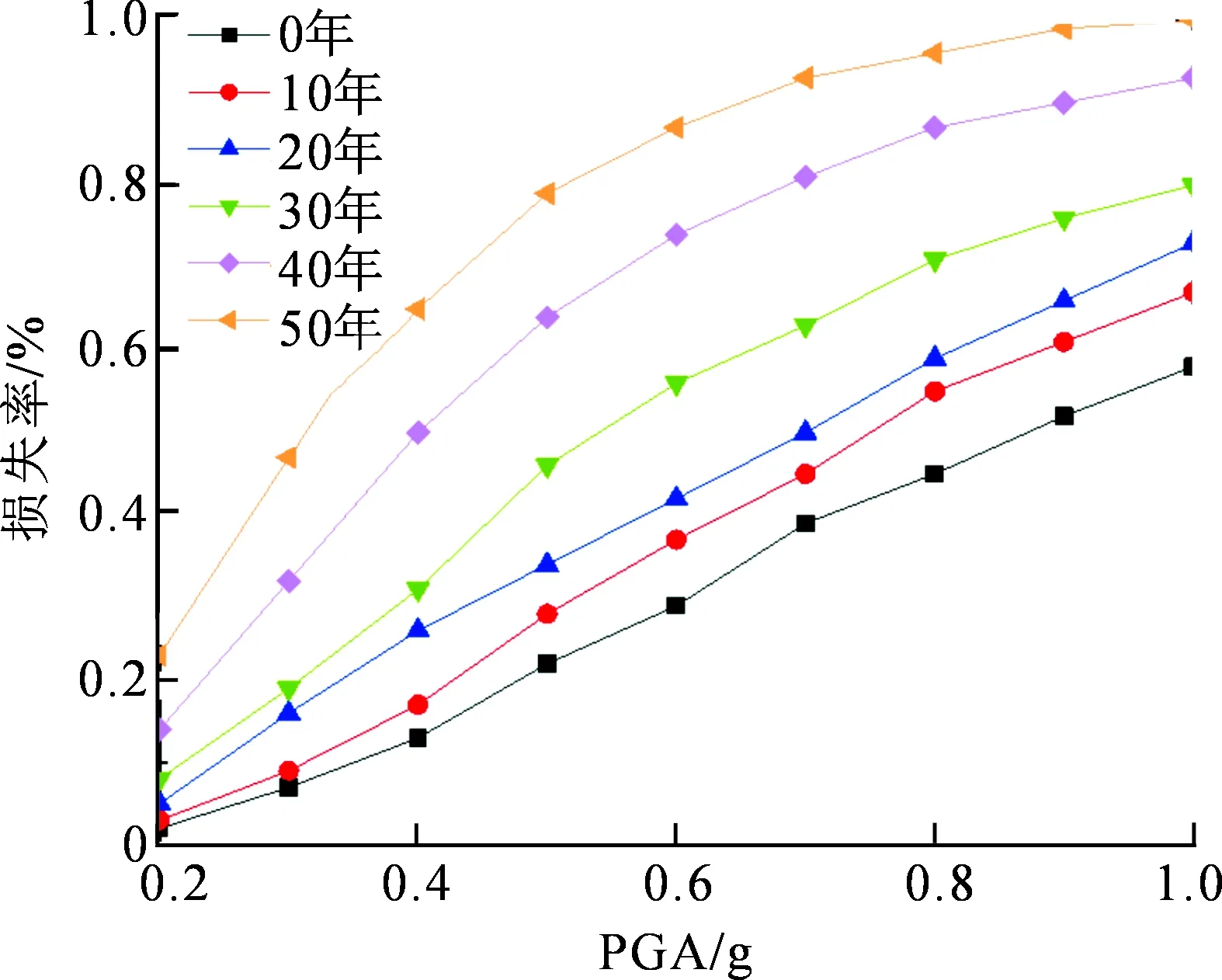
图9 损失率随PGA的变化
图10给出了同一地震强度下受氯离子侵蚀的不同服役时间的RC框架结构时变抗震可恢复性变化。例如,当PGA=0.3 g时,服役不同年限下的框架结构在地震作用后的可恢复概率分别为94.59%,93.90%,91.21%,89.15%、83.25%,75.23%;当PGA=0.5 g时,服役不同年限下的框架结构在地震作用后的可恢复概率分别为87.47%,85.48%,81.35%,76.25%,73.25%,60.15%,可以看出,随着氯离子侵蚀作用的不断增加,钢筋混凝土框架结构可恢复性逐渐降低。

图10 同地震强度下RC框架结构时变抗震可恢复性
4 结 论
1) 通过考虑氯离子不同侵蚀时间对钢筋力学性能的影响,建立了钢筋截面损失模型,并进一步通过建立力学性能退化表达式获得了氯离子侵蚀下钢筋混凝土结构的地震损伤模型以及相应地震破坏状态的划分。在此基础上,综合考虑结构的直接损失与间接损失,建立RC框架结构损失函数。
2) 基于OPENSEES有限元分析软件,对不同锈蚀时间的RC框架结构进行建模分析,结果表明:在氯离子侵蚀环境的影响下,RC结构的抗震性能随着服役时间的增加而不断劣化。当钢筋混凝土结构在不同服役时间遭遇同一地震强度时,其同一破坏程度的超越概率具有显著的增加,钢筋混凝土框架结构可恢复性逐渐降低。

