互联网时代零售业上市公司资本资产定价模型研究

燕 群，蓝发钦

(华东师范大学经济与管理学部，上海 200062)

互联网技术是新一代技术革命的核心生产力，已经直接在生产、流通和消费活动中创造价值[1]。新冠肺炎疫情下，互联网零售在现代零售业中的地位突增。同时，互联网技术正在重塑零售业生产经营与销售盈利的传统业态，从商务模式、产品销售和服务创新等方面创造价值[2]。那么，互联网技术是否已经影响了资本资产的价值？Liran和Jonathan[3]提出，以互联网技术为代表的数字经济技术势必导致金融学模型的适用性发生颠覆性的变化[4][5]。近年来，互联网时代商业模式的重塑与价值创造理论的研究已经引起国内外学术热议[6][7][8][9]，如果互联网技术溢价已经存在于资本市场，那么资本资产定价模型的适用性将遇到挑战。

CAPM单因子模型[10][11][12]和Fama-French三因子模型[13]是基础的资本资产定价模型，也是金融学的基石模型，模型的实证与修正一直以来都是金融学研究热点[14][15]。多数学者提出纳入其他因子以增强单因子模型和三因子模型的解释力，如财务杠杆[16]、股票市净率[17]、市场权益[18]、股票品质[19]和股票流动性等[20]。以上因子之所以被纳入资本资产定价考量，是因为它们具备资本资产的收益溢价创造功能。1989年，Fama和French提出不同时期(例如美国大萧条时期)商业模式的差异可以作为资本资产定价模型的影响因子[21]，这为本文探讨互联网时代背景下，零售业上市公司资本资产定价模型的适用性与模型修正的方法奠定了基础。

一、问题的提出

(一)互联网技术的价值创造

移动互联网时代的商业模式所打造的企业是新技术变革中互联网赋能的新经济企业[22]，互联网技术价值创造功能的主要表现包括：构建互联网平台联系万物，使供给与需求快速融通，市场更加高效；依托线上销售模式降低实体经营成本，通过足不出户的消费体验提升消费者的购买意愿和黏性；促进文件和信息形态加入生产过程，使公司能低成本实现个性化生产支持体系的塑造；以互联网资产形态(“网红”资产、消费行为数据等)作为生产要素替代其他资产创造价值；借助互联网系统支持企业运营，重塑生产链、打破职能部门界限。图1以Porter[23]提出的公司经营活动价值创造链条为基础，重塑了融入互联网生产要素的零售业上市公司经营与价值创造链条。

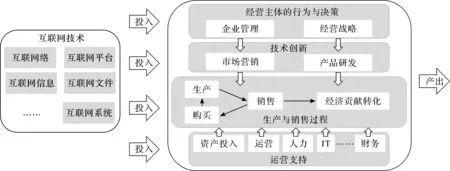
图1 互联网技术重塑零售业上市公司经营与价值创造链条

(二)实证逻辑

基于互联网技术价值创造的事实，下一步验证互联网技术是否影响了零售业上市公司股票价格。1997年，亚马逊在纳斯达克上市，揭开了互联网零售行业公司上市序幕。2014年，京东集团在纳斯达克上市。2015年以来，互联网零售业上市公司的数量和市值大幅增长，增速远超非互联网零售业上市公司。截至2020年3月末，互联网零售业在全球各大交易所上市的公司共58家，零售业上市公司共245家(1)行业分类标准参照Wind分类，互联网零售业是三级行业分类，其所属一级行业为可选消费，二级行业为零售业。(见表1)。伴随互联网零售业的发展，在国内外股市互联网零售业已成为一个细分行业。借鉴Fama-French三因子模型[13]的研究思路，后续研究将运用三因子模型“因子分组—矩阵构建—收益率回归”的研究范式，聚焦零售业上市公司，在三因子模型分组的基础上增加互联网零售业、非互联网零售业分组，论证零售业上市公司股票价格中是否存在互联网技术溢价，提出将互联网技术溢价计入资本资产定价模型的方法。

表1 互联网零售业上市公司情况

二、实证分析

(一)样本描述

本文选取2015年1月以前在纳斯达克上市的零售业上市公司，满足数据完整性要求的样本共64家，其中互联网零售业上市公司23家(样本组合I)，非互联网零售业上市公司41家(样本组合R)；选取各季度末最后一个交易日的季度收益率来获取股票收益率时间序列，构建2015年1月至2020年3月的面板数据集，时间序列的样本数据共21组。数据均来源于Wind数据库。

(二)三因子模型实证

研究运用三因子模型拟合各样本时间序列收益率，以此作为基准对比分析互联网技术对股票价格的溢价。表2三因子模型(2)Fama和French(1973)三因子模型分别以上市公司规模(总市值指标)、账面/市值比指标对样本进行分组，构建矩阵，用矩阵收益率差值作为模型参数训练模型，最终求得股票拟合收益率。研究参照Fama和French的分组方法，根据总市值的中位数，将样本分为B(大规模)、S(小规模)两组，根据账面/市值比的三分之一位数、三分之二位数，将样本分为L(低账面/市值比)、M(中等账面/市值比)和H(高账面/市值比)三组，构造2*3矩阵。以上分组以各年末数据调整，计算期内合计调整了5次。拟合效果表明，互联网零售业(样本组合I)与非互联网零售业(样本组合R)各矩阵中，三因子模型拟合R2值均小于0.80，且超过50%的矩阵拟合R2值小于0.50，这说明三因子模型拟合效果不显著。

表2 三因子模型拟合R2值

表3刻画了时间序列下三因子模型拟合收益率与实际收益率的差值。该差值的绝对值越小，表示三因子模型拟合效果越好，反之则反。对于样本组合I，2015—2020年，除BM矩阵、SH矩阵外，其他4个矩阵差值的绝对值明显提升，且2019—2020年提升最为显著。对于样本组合R，2015—2020年，6个矩阵差值的绝对值均明显下降。以上结果表明：对于互联网零售业上市公司，三因子模型的拟合效果已明显下降，而对于非互联网零售业上市公司，三因子模型的拟合效果依旧显著；新增是否为互联网零售业作为分组的因子，可能增强资本资产定价模型的拟合效果。

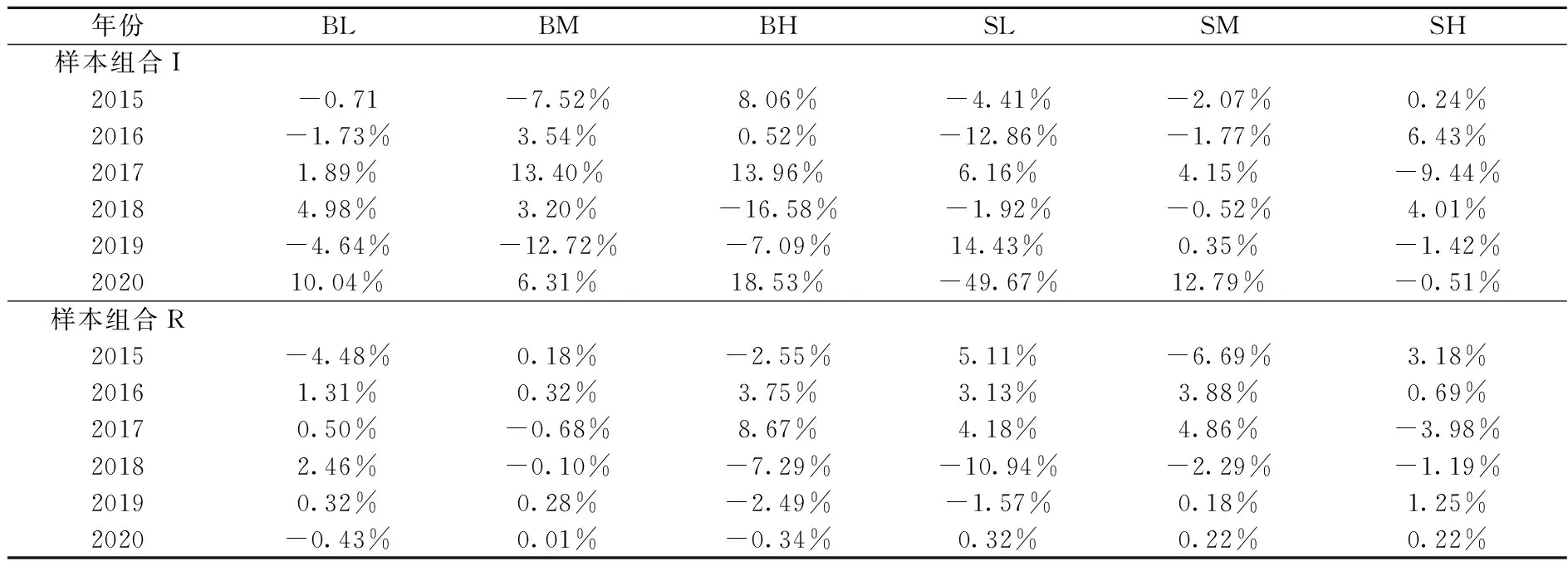
表3 时间序列三因子模型描述性统计

(三)互联网技术溢价与四因子模型实证

本文运用三因子模型的研究范式，在三因子基础上新增互联网技术渗透度作为第四个分组因子，根据是否为互联网零售业，将样本分为O(互联网零售业)、N(非互联网零售业)两组，构造2*2*2的时间序列矩阵(见表4)，四因子模型如下：

R-Rf=βMarket(Rm-Rf)+βSMB(SMB)+βHML(HML)+βOMN(OMN)+α

(1)

式中，βMarket、βSMB、βHML和βOMN分别代表市场因子、规模因子、账面/市值比因子、互联网技术渗透度因子的回归系数；R表示模型所求的股票拟合收益率；Rm是市场组合收益率，通过全部样本收益率的均值计算；Rf是无风险利率，选择1个月期限的国债收益率；SMB表示小市值股票组合收益率与大市值股票组合收益率的差值；HML表示高账面/市值比股票组合收益率与低账面/市值比股票组合收益率的差值；OMN表示高互联网技术渗透度股票组合收益率与低互联网技术渗透度股票组合收益率的差值；α表示股票的超额收益率。

表4 四因子模型矩阵的构建

表5四因子模型运行结果说明，零售业上市公司股票价格存在明显的互联网技术溢价，四因子模型拟合股票收益率的R2值相比于三因子模型(见表2)有大幅提升，说明四因子模型测度零售业上市公司股票价格具备有效性。具体来看，大规模且高账面/市值比的零售业上市公司组合R2值为0.94、高账面/市值比的互联网零售业上市公司组合R2值为0.91，高于全部组合R2值的均值0.82，表明这两个组合四因子模型拟合效果最显著；大规模的非互联网零售业上市公司组合、低账面/市值比的互联网零售业上市公司组合的R2值均低于全部组合R2值的均值0.82，表明这两个组合四因子模型拟合效果最弱，但超过了三因子模型拟合R2值的均值0.46(见表2)。同时，表5和表6的结果说明，四因子模型中因子间两两相关关系不显著，证实四因子模型通过内生性检验。

表5 四因子模型拟合R2值与因子载荷(2015年1月—2020年3月)

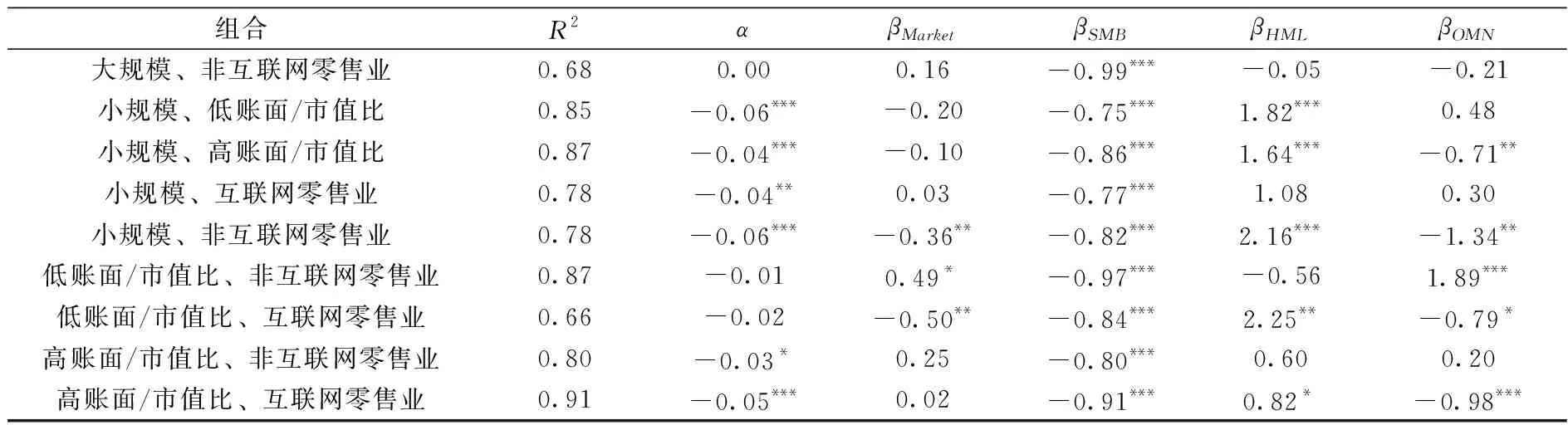
续表

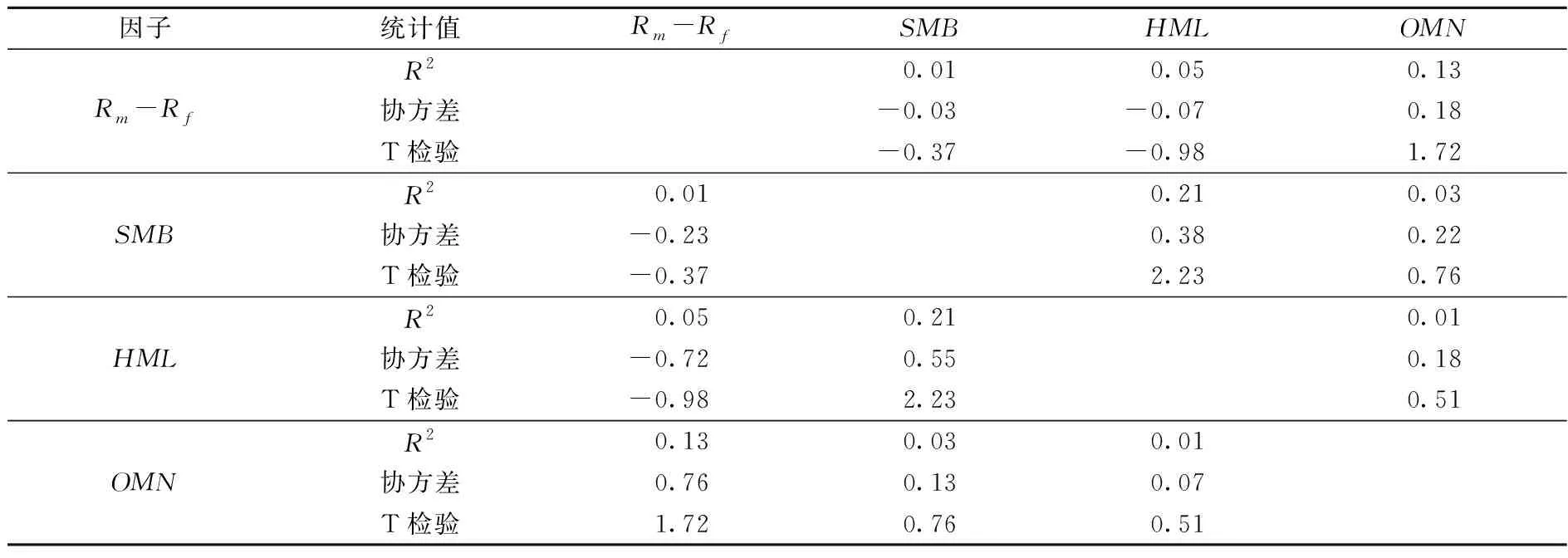
表6 内生性检验

对资本资产定价模型的讨论是金融学理论研究的重要分支，新模型的提出是对模型的重新审视。学界过往探讨资本资产定价模型的适用性主要集中于βMarket是否能解释股票收益率在横截面上的变动。Banz[24]、Fama和French[13]通过新增影响因子证实βMarket不足以解释股票收益率的变动。Kothari等[25]通过研究βMarket的取值范围，从βMarket在置信区间内取值范围较大说明其不足以解释股票收益率的变动。四因子模型的βMarket取值范围波动较大，侧面证实了Kothari等[25]的结论。Fama和Fench[13][26]在构建三因子模型和五因子模型的过程中，曾提出账面/市值比对股票收益率的影响程度超过市场因子和规模因子，但是表5各因子相关分析的显著性结果并不支持这一观点，反而支持规模因子是四因子模型中影响最为显著的因子，各样本组合规模因子均在0.1%置信水平下显著，显著性特征明显超过其他因子。

近年来大量实证研究聚焦于资本资产定价模型的“异象”。为了进一步讨论不同市场环境下四因子模型的“异象”特征，本文将研究时间段Ta分为纳斯达克指数上升时间段Tu1(2015年1月至2018年5月)、上升时间段Tu2(2019年5月至2020年2月)、震荡时间段Tf(2018年5月至2019年5月)和下跌时间段Td(2020年2月至2020年3月)，如图2所示。关于“异象一”：高账面/市值比组合的股票比低账面/市值比组合具有更高的收益，可用特定研究期论[2]、风险因素论[27][28]、公司特征决定论[29]及不同股票市场的特性[30]来解释。表7结果显示，在不同市场环境下四因子模型的变量数理特征并未有明显的账面/市值比规律，支持特定研究期论，证实账面/市值比效应只是特定样本在特定检验期内才存在，是数据挖掘的结果。关于“异象二”：小规模且高账面/市值比组合的股票收益率在不同市场环境下高于其他组合[29]，表7结果支持公司特征决定论，四因子模型同样存在规模与账面/市值比的组合特征，在不同市场环境下，小规模且高账面/市值比的组合收益率均高于其他组合，同时在纳斯达克指数震荡时间段Tf，该“异象”特征更加明显。

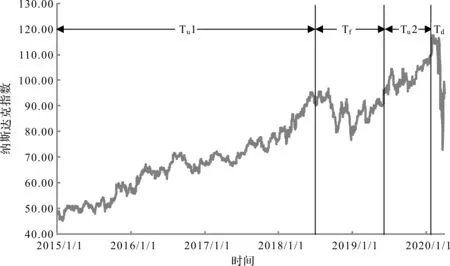
图2 研究时间段的划分

深入分析发现，四因子模型还存在其他“异象”特征：一是规模因子与互联网技术渗透度因子的组合特征。由表7收益率平均值可知，在不同市场环境下小规模互联网零售业上市公司的股票收益率高于其他组合。二是收益率波动的特征。由表7收益率标准差可知，一方面，在纳斯达克指数震荡时间段Tf，各组合的股票收益率波动较明显，另一方面，小市值且低账面/市值比、低账面/市值比的互联网零售业组合的股票收益率波动率较低，小市值且高账面/市值比、高账面/市值比的非互联网零售业组合的股票收益率波动率较高。

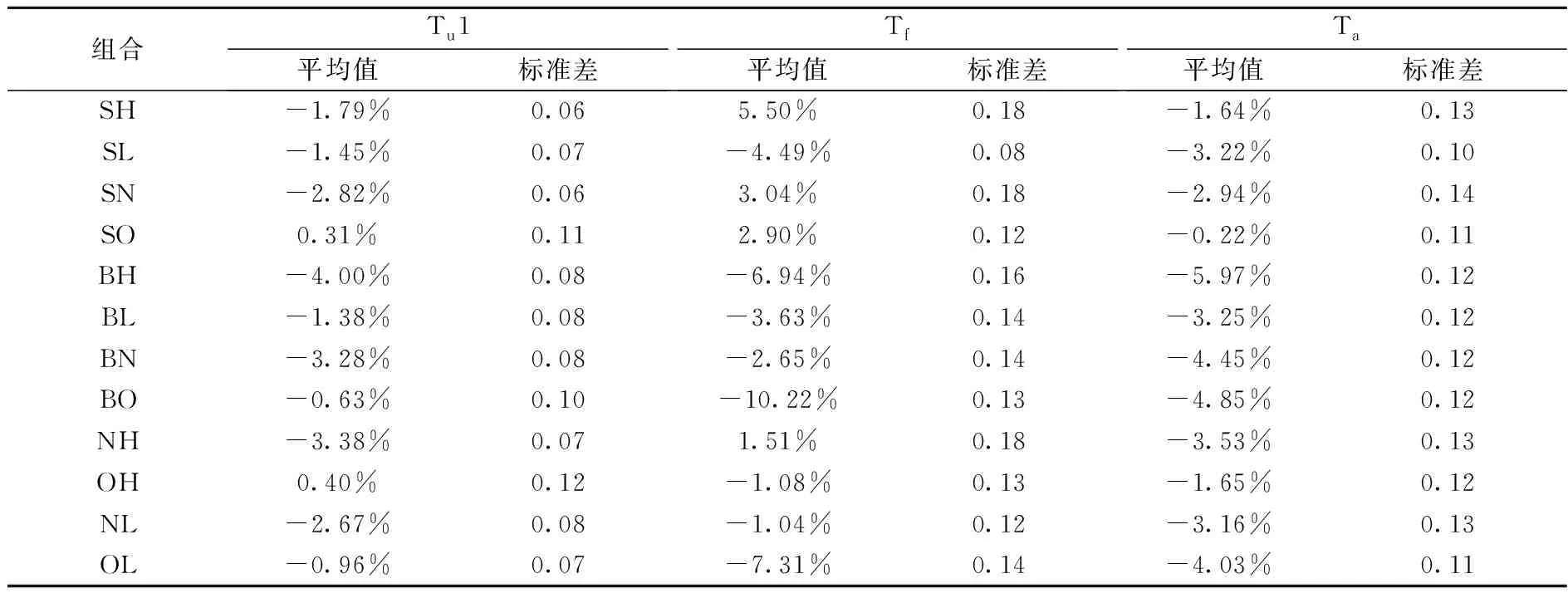
表7 四因子模型描述性统计

表8刻画了时间序列下四因子模型拟合收益率与实际收益率的差值情况。2019年前后，收益率差值的均值没有发生显著变化。比较表3三因子模型拟合收益率发现，2019年之后互联网技术渗透度对三因子模型拟合效果的影响越来越大，模型拟合效果明显下降，但四因子模型的拟合效果相对稳定。

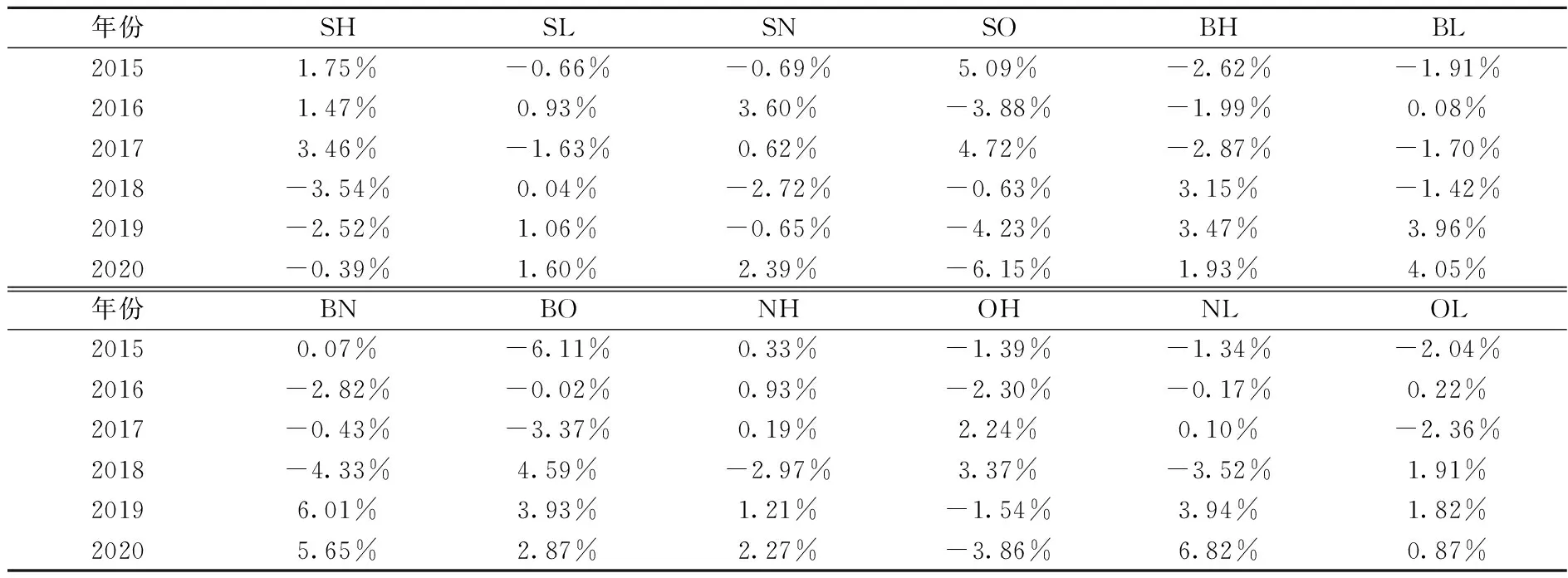
表8 时间序列四因子模型描述性统计

(四)互联网技术溢价的产生机制

Fama和Macbeth曾提出用截面回归的方法(简称FM回归)[30]检验三因子模型因子载荷特征。本文在该方法基础上，将被解释变量设定为各矩阵股票的平均收益率。表9第1组控制变量为市场因子载荷、规模因子载荷和账面/市值比因子载荷，解释变量为互联网技术渗透度因子载荷；第2组控制变量为互联网技术渗透度因子载荷，解释变量为市场因子载荷、规模因子载荷和账面/市值比因子载荷；第3组将所有因子载荷纳入解释变量。

从表9第1组结果可知，股票收益率与互联网技术渗透度因子载荷不存在显著相关性，说明互联网技术不直接影响股票收益率，即并不是互联网技术渗透度越大，股票收益率就越高。第3组的互联网技术渗透度因子载荷在5%水平下显著，说明互联网技术价值创造是通过影响其他因子的价值创造过程实现的。对比第2组与第3组结果显示，三因子模型中市场因子载荷显著性特征不明显，而四因子模型中市场因子载荷在1%水平下显著，同时规模因子载荷和账面/市值比因子载荷保持在1%的水平下显著，这再次验证了四因子模型拟合显著性优于三因子模型。

表9 基于Fama-Macbeth的因子载荷回归结果

(五)稳健性检验

李和金与李湛[31]曾提出，收益率计算截面的选取会影响模型的有效性，据此本部分选取不同的截面计算收益率，用相同面板数据时间段的不同时间序列重复检验四因子模型的稳健性。将前述研究的收益率截面定义为截面1；新增稳健性检验截面2，获取各季度末最后一个交易日股票价格相对于上月最后一个交易日股票价格的月度收益率，得到21组收益率数据；新增稳健性检验截面3，获取各月末最后一个交易日股票价格相对于上月最后一个交易日股票价格的月度收益率，得到63组收益率数据。

表10显示三个截面下的拟合R2值，结果表明四因子模型在截面2和截面3条件下的拟合效果同样显著，说明四因子模型通过稳健性检验。进一步分析发现，截面2条件下模型总体拟合效果优于截面1，截面3条件下模型总体拟合效果劣于截面1。具体而言，截面2条件下，仅2个组合的拟合R2值小于0.80。但是截面3条件下，全部组合的拟合R2值均小于0.80，且有6个组合小于0.50。这说明截面3条件下模型拟合效果最不稳定。

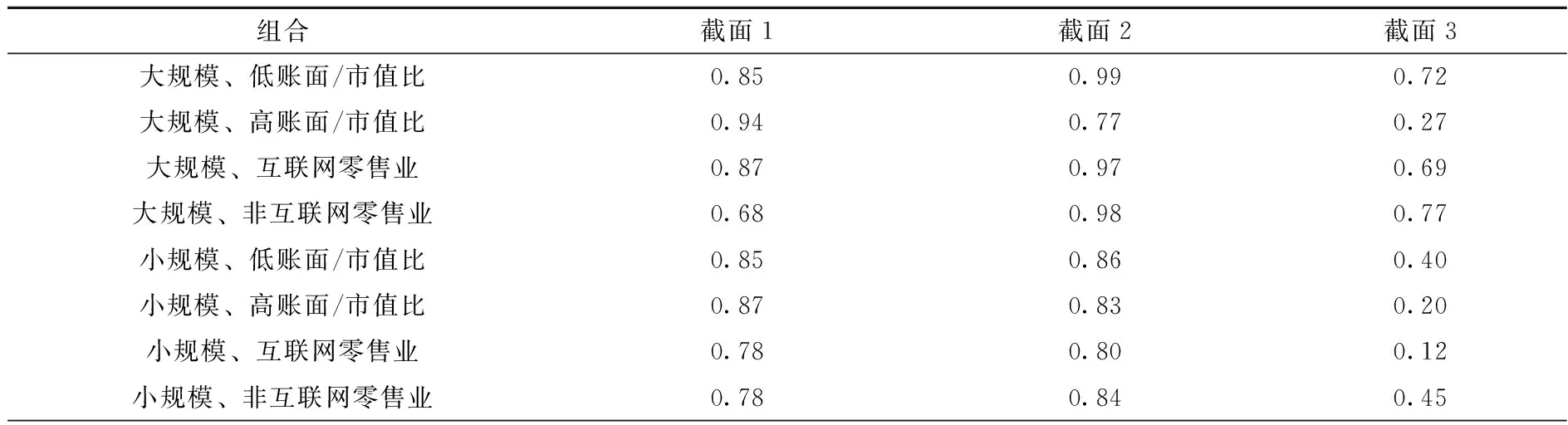
表10 四因子模型稳健性检验

续表

三、进一步分析

为分析四因子模型在危机行情下的适用性与稳定性，接下来以新冠肺炎疫情冲击下的市场行情为例，测试四因子模型的有效性。

(一)数据处理

研究样本统一采用纳斯达克上市的64家零售业上市公司，研究数据选取2020年1月至2020年2月，收益率截面选取每个交易日的月收益率，因此该时间序列数据包含37组股票收益率。以上数据均来源于Wind数据库。

(二)异质性分析

表11显示了2020年1月至2020年2月新冠肺炎疫情冲击期间四因子模型拟合股票收益率的情况。相较于表5的2015年1月至2020年3月期间四因子模型拟合效果，从各因子回归显著性水平和拟合R2值两个角度，结果均显示疫情期间四因子模型拟合效果优于该模型在2015年1月至2020年3月的拟合效果。

陈浪南和屈文洲[32]认为市场因子解释力存在异质性，在大盘指数波动剧烈，特别是急速上升的时间段，市场因子对股票收益率的影响远高于其他时期。表11与表5的分析结果表明，四因子模型支持陈浪南和屈文洲[28]的结论，即在大盘急速上升的行情下，市场因子对股票收益率的影响提升，账面/市值比因子对股票收益率的影响下降，市场因子取代账面/市值比因子成为股票收益率最主要的决定因素。此外，表11的结果也显示了四因子模型的其他异质性特征：第一，相比于表5，低账面/市值比的股票在疫情期间拟合R2值高于高账面/市值比的股票，大规模的股票高于小规模的股票；第二，相比于表5，新冠肺炎疫情冲击行情下，四因子模型对互联网零售业上市公司股票收益率的拟合效果提升，并且对互联网零售业股票收益率拟合效果优于非互联网零售业。

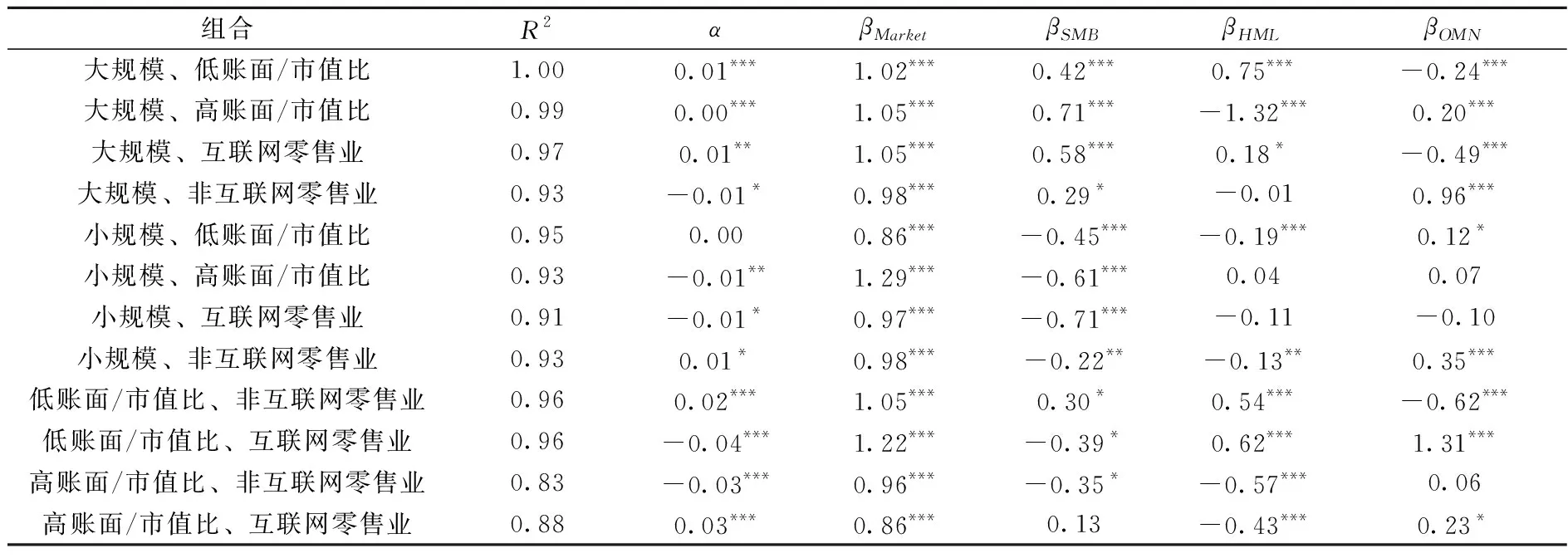
表11 四因子模型拟合R2值与因子载荷(2020年1月—2020年2月)

同时本文通过拟合收益率与实际收益率的差值分析，探究四因子模型的稳定性。图3结果显示，收益率差值的波动性与组合收益率的波动性基本一致，但是波动的方向可能相反；相对于组合收益率上涨期，组合收益率下跌期收益率差值的波动性更大。

图3 四因子模型拟合收益率与实际收益率差值

进一步分组分析危机行情下，四因子模型对于互联网零售业上市公司与非互联网零售业上市公司的适用性差异。图4显示互联网零售业上市公司拟合收益率与实际收益率差值，大规模(BO)、低账面/市值比(OL)的股票收益率差值走势一致，并且与小规模(SO)、高账面/市值比(OH)的股票收益率差值走势相反。图5显示非互联网零售业上市公司拟合收益率与实际收益率差值，结果与图4总体一致，差别在于大规模的非互联网零售业股票与互联网零售业股票收益率差值走势相反，低账面/市值比的非互联网零售业股票与互联网零售业股票收益率差值走势相反，对于小规模股票、高账面/市值比股票亦存在相同情况。

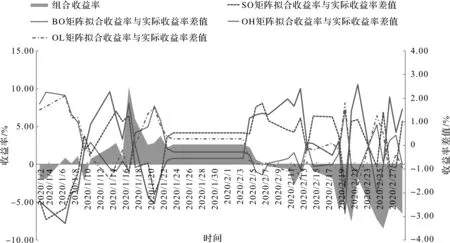
图4 互联网零售业上市公司拟合收益率与实际收益率差值

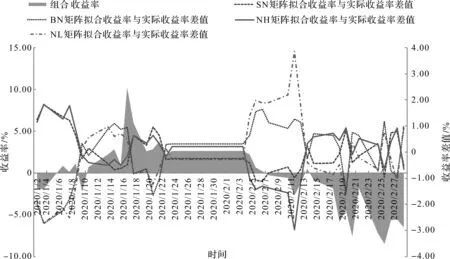
图5 非互联网零售业上市公司拟合收益率与实际收益率差值

四、结论与启示

互联网时代背景下，互联网技术已经影响了零售业上市公司资本资产的价值，为此本文探讨了Fama-French三因子定价模型的修正思路，得到如下结论：第一，互联网技术溢价存在于零售业上市公司，四因子模型在研究期内拟合效果优于三因子模型；第二，对于大规模、高账面/市值比的零售业上市公司以及高账面/市值比的互联网零售业上市公司，四因子模型拟合效果更加显著；第三，在以新冠肺炎疫情冲击为代表的危机行情下，四因子模型通过了异质性检验，并且模型拟合效果优于非疫情时期。

本文提出了零售业上市公司的四因子资本资产定价模型，实证结果通过了不同研究时间段、不同收益率截面下四因子模型的稳健性检验和异质性讨论。本文立足于Fama-French三因子模型，研究方法借鉴三因子模型拓展模型的推演思路，但这只是时代背景下重新探讨金融学模型的起点，希望此研究为互联网时代金融学模型的修正提供借鉴思路。非理性市场假设下，APT[33]、特征模型[29]的改进将是更进一步的探索方向。此外，传统的生产要素理论、市场均衡理论及要素生产领域的资产定价(TFP)等也需要重新解读，相关金融学模型的修正同样具备重要研究价值。