顾及区域相对高程的中国区域加权平均温度模型
韦海福 陈天伟 陈 明
1 桂林理工大学测绘地理信息学院,桂林市雁山街319号,541006
水汽是地球大气的重要组成之一,主要分布在对流层内。水汽在全球水循环、气候变化和灾害性天气演变中扮演着重要角色,因此对大气中水汽的时空变化趋势分析具有重要意义。随着全球导航卫星系统(GNSS)的发展,具有全天候、高精度、高时空分辨率等优点的GNSS水汽探测已逐渐成为气象学领域的热点之一。大气加权平均温度(Tm)是GNSS水汽探测中的重要因素,也是计算可降水量(PWV)的关键参数[1],可通过探空资料或大气再分析资料计算得到,但无法满足用户实时获取任意位置Tm值的需求,因此需建立高精度的Tm模型。Bevis等[1]认为,Tm与地表温度(Ts)之间存在很强的线性关系,并建立了线性回归公式(Bevis公式);随后,诸多学者通过研究发现,Tm与Ts的关系会随地区和季节发生变化,随即建立了不同地区的线性回归模型[2],通过周期函数拟合Tm模型残差,减弱了残差季节性变化带来的周期性误差影响[3];而在垂直方向上,Bevis公式随着地表海拔的升高,精度逐渐降低[4];黄良珂等[5]利用ERA-Interim分层大气资料分析中国区域Tm随高程的变化情况,构建了顾及季节变化的Tm垂直递减率中国区域大气加权平均温度模型。
对流层顶作为对流层与平流层之间的过渡层,在对流层与平流层交换气团、水汽、能量等过程中发挥着重要的作用[6-8]。中国区域疆域辽阔,气候多样化,且地形起伏较大,尤其是在中国西部高海拔地区,已有的Tm模型大多精度偏低,因此需建立中国区域高精度的Tm新模型。本文基于已有的对流层顶经验模型,利用中国区域内的探空站数据,对中国区域相对高程与加权平均温度的关系进行分析,构建了一种顾及区域相对高程h0的双因子(h0、Ts)非线性Tm模型(h0Tm模型),并利用ERA5格网数据和探空数据验证该模型的精度,以期为中国区域高精度GNSS水汽探测提供参考依据。
1 数据来源及模型建立
ERA5是欧洲中尺度天气预报中心(ECMWF)提供的第5代数据集,能提供时间分辨率为1 h、空间分辨率为0.25°×0.25°的地面和高空气象数据;探空站可提供时间分辨率为12 h的实测地表数据和分层气象参数,常用来评测其他产品和模型的精度。本文使用2015~2018年覆盖中国陆地区域的时间分辨率为6 h(0时、6时、12时、18时)、空间分辨率为0.25°×0.25°的ERA5地面和高空气象资料和分布于中国区域的89个探空站数据进行模型的构建和分析,其中ERA5地面气象资料包括位势、气压、2 m温度、2 m露点温度等;高空气象资料根据气压分层,每个格网点上选取底层气压为1 000 hPa、层顶气压为30 hPa共27层数据,包括位势、气压、温度、比湿等。
1.1 对流层顶的确定方法
目前确定对流层顶常用的方法为弯曲角对数协方差变换法[9],即利用掩星数据得到精度较高的对流层顶参数。在全球范围内掩星事件1 d可达上千次,发生在中国区域的掩星事件却只有十几次,空间分辨率较低且计算过程过于繁杂。因此,本文选用基于掩星数据构建的全球对流层顶经验模型计算对流层顶高度[10],该模型的核心方法是采用稳健协方差转换,用于获取指定时间某一纬度的对流层顶高度。模型具体形式为:
g(t,φ)=a0(t)+a1(t)cos(ω(t)φ)+
b1(t)sin(ω(t)φ)
(1)
式中,g(t,φ)为对流层顶高度,a0、a1、b1为待拟合系数,φ为纬度,t为年积日,ω(t)为频率。系数拟合函数见表1。

表1 系数拟合函数
1.2 模型构建
根据Tm的积分定义式,可将对流层顶作为积分定义式的上限[8]。设地面点为hs,对流层顶高为h′,则积分定义式的区间为[hs,h′],区域相对高程为h0=h′-hs。
图1为利用2015~2017年中国地区89个探空站观测数据获得的地表温度、区域相对高程与加权平均温度的散点分布,其中红色线为拟合线。由图可知,h0与Tm的分布呈明显的二次函数关系,相对于Ts与Tm,其散点分布较为离散。将h0作为自变量进行拟合得到的二次函数模型的模型均方根误差(RMS)为6.03 K,相关系数为0.69;以Ts为自变量得到的线性函数所产生的RMS为4.18 K,相关系数为0.82,两者的模型均方根误差相差不到2 K,且以h0为自变量的模型同样具有较高的相关性。因此,本文采用线性和非线性相结合的方式将Ts和h0作为参数进行拟合,构建顾及区域相对高程h0的加权平均温度非线性回归模型,以获取精确的加权平均温度。
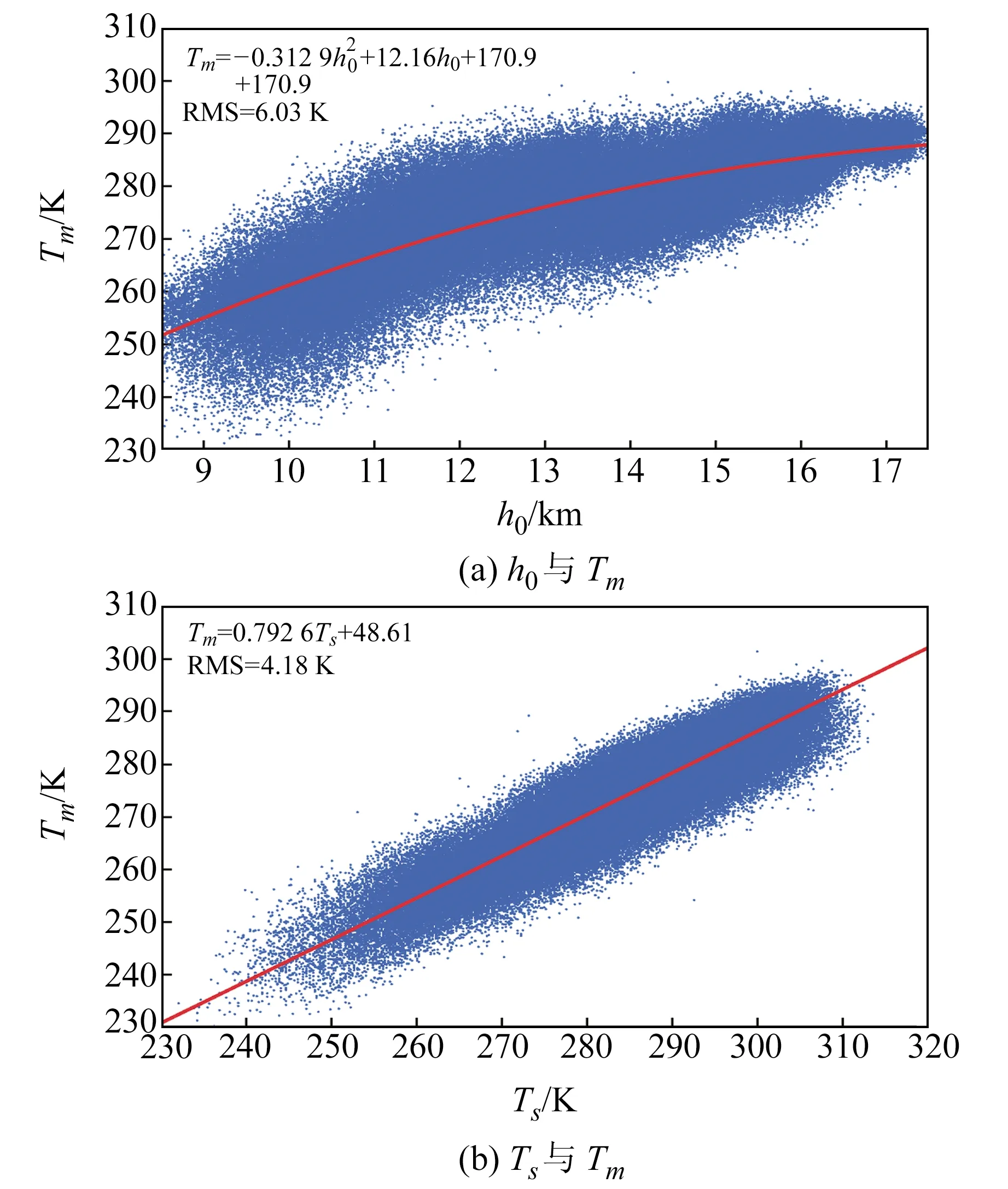
图1 Tm与Ts和h0的分布
本文建立中国区域顾及区域相对高程h0的加权平均温度非线性回归模型公式为:
(2)
式中,Ts为地面温度,h0为区域相对高程,a1、a2、a3、a4为模型拟合系数。
选择2015~2017年覆盖中国陆地区域的时间分辨率为6 h、空间分辨率为0.25°×0.25°的ERA5地面和高空气象资料进行模型拟合,其中计算h0Tm模型所需的地表温度Ts由ERA5地面气象资料中的2 m温度代替,计算h0所需的地面点高程hs由地面资料中的位势计算得到。以每个格网点为最小单位,利用回归分析求取各格网点的回归系数,具体步骤为:1)通过Tm的积分定义式求得各格网的Tm积分值;2)对式(2)进行回归分析,得到格网点回归系数。为进行比较,对各格网点单变量模型TsTm(TsTm=b1+b2Ts)进行回归分析,并对两者模型的相关性进行对比。由于h0Tm为非线性模型,这里选择决定系数R2来验证模型的拟合回归效果。
如图2所示,h0Tm模型和TsTm模型的R2整体随纬度的增加逐渐升高,TsTm模型在青藏高原等高海拔地区的R2较平坦地区低,而h0Tm模型的R2在中国大陆地区普遍较高。由此可知,在加入变量区域相对高程h0后,h0Tm模型的拟合回归效果相对于单变量模型TsTm有较大提升。
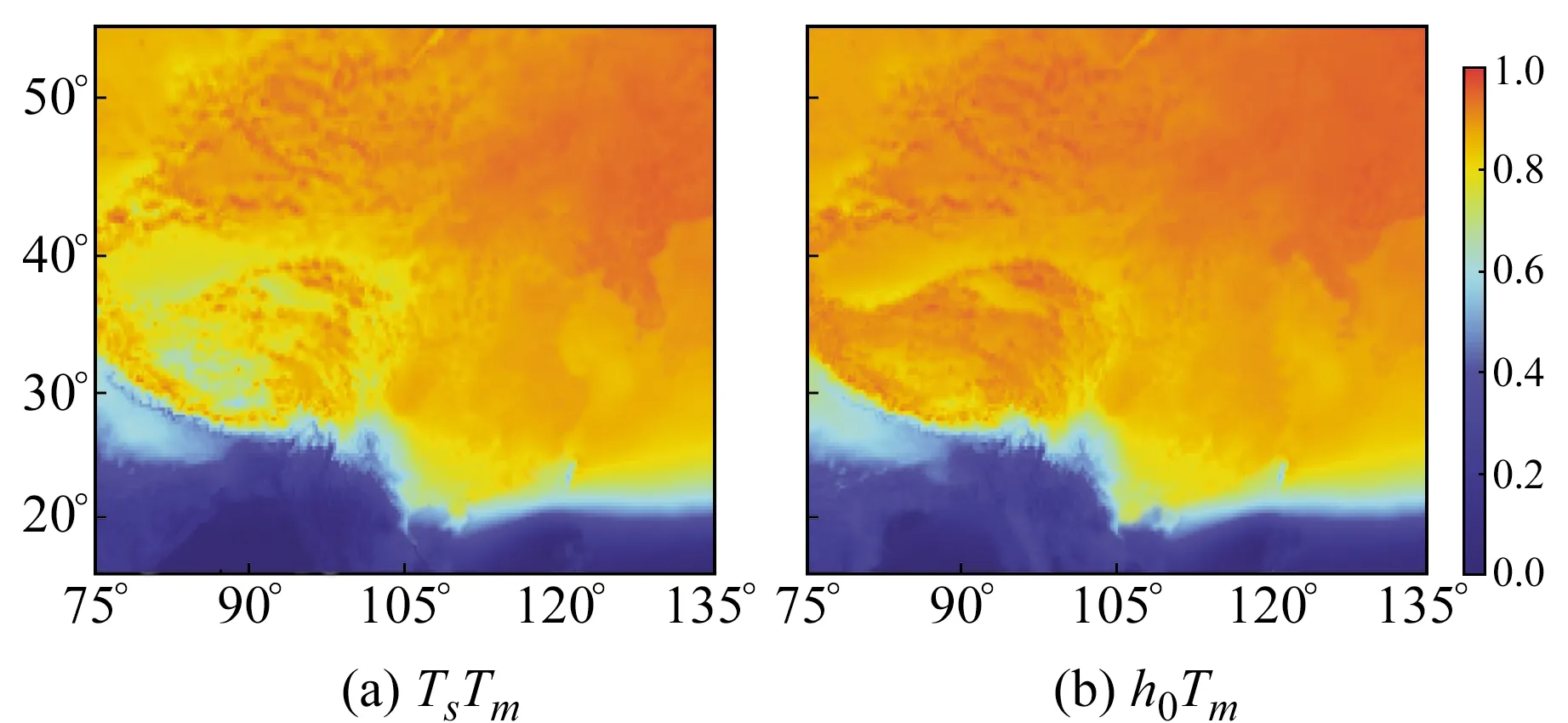
图2 回归模型的决定系数R2
2 模型精度验证
本文以ECMWF提供的2018年ERA5格网产品积分得到的Tm值和2018年中国区域的89个探空站数据作为参考值,对模型进行精度评估,评估指标为偏差(bias)、绝对平均偏差(MAD)及均方根误差(RMS):
(3)
(4)
(5)
2.1 使用ERA5格网积分Tm值进行精度验证
利用2018年覆盖中国区域的ERA5格网产品积分得到的Tm值作为参考值,验证h0Tm模型的精度,同时与运用广泛的Tm线性模型Bevis公式(Tm=70.2+0.72Ts)和性能较优的对流层延迟改正模型GPT2w-1进行对比分析。GPT2w模型是一个全球经验对流层格网模型,可提供水平分辨率为1°×1°(GPT2w-1模型)和5°×5°(GPT2w-5模型)的对流层湿延迟、地表温度、地表气压等对流层参数,GPT2w模型在计算Tm时无需实测气象参数,其中GPT2w-1模型的精度和稳定性优于GPT2w-5模型[11]。Bevis公式计算Tm所需的Ts可由ERA5地面气象资料中的2 m温度代替计算。不同模型的年均bias、MAD和RMS值统计结果见表2(单位K)和图3。

表2 利用ERA5积分值验证h0Tm模型、GPT2w-1模型和Bevis公式的精度对比
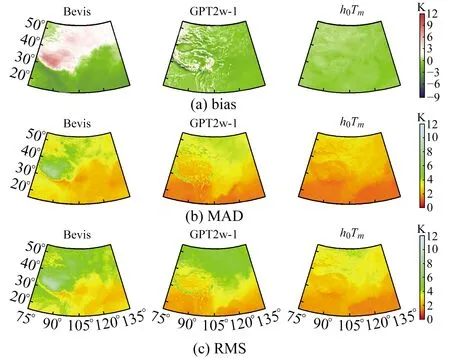
图3 利用2018年ERA5格网积分Tm值检验中国区域不同模型的bias、MAD和RMS分布
由表2可知,GPT2w-1模型的正偏差最大值为11.35 K、负偏差最大值为-9.67 K,Bevis公式具有最大的MAD年均值(2.90 K),h0Tm模型在中国地区表现出较小的偏差;在RMS方面,Bevis公式表现出最大的RMS年均值,h0Tm模型的RMS年均值最小(2.43 K),相对于Bevis公式与GPT2w-1模型,精度分别提高了1.15 K(32%)和0.63 K(21%)。
由图3可以看出,Bevis公式与GPT2w-1模型在中国西部地区均存在较大的偏差,而h0Tm模型在中国区域整体偏差较小,表现出良好的稳定性;Bevis公式在中国西部,尤其是青藏高原地区存在较大的RMS值,GPT2w-1模型在青藏高原地区同样表现出较大的RMS值,这是因为Bevis公式是用美国探空站数据建立的经验模型,在中国地区适用性不足,而GPT2w-1模型在建立时未考虑Tm的高程改正问题,导致其在高海拔地区存在显著的误差。h0Tm模型顾及了Tm计算区域的相对高度h0,因此在地形起伏较大的地区同样保持着较高的精度。由此可知,h0Tm模型在中国区域使用时能表现出较高的精度和良好的稳定性。
2.2 使用探空站数据进行精度验证
选取2015~2017年均匀分布在中国区域的89个探空站实测数据构建各探空站的站点模型,并利用2018年探空站数据积分得到的Tm值作为参考值,验证h0Tm模型的精度。不同模型年均bias、MAD和RMS值统计结果见表3(单位K)和图4。

表3 利用探空站数据验证h0Tm模型、GPT2w-1模型和Bevis公式的精度对比
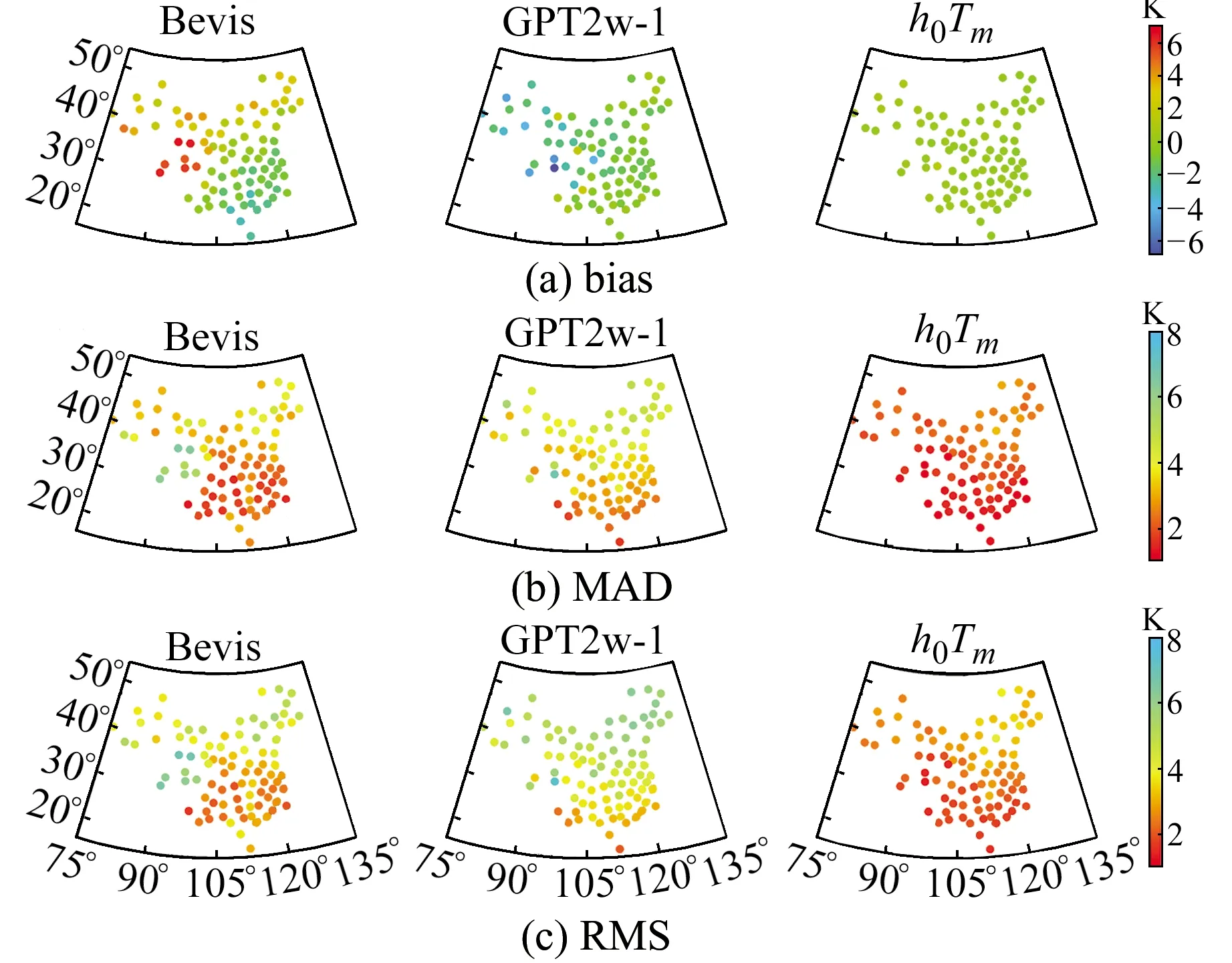
图4 利用2018年探空站数据检验中国区域不同模型的bias、MAD和RMS分布
由表3可知,Bevis公式出现较大的正偏差,GPT2w-1模型存在较大的负偏差,且具有最大的MAD年均值(3.60 K),而h0Tm模型偏差较小;GPT2w-1模型表现出最大的RMS值(年均值为4.62 K),h0Tm模型RMS年均值最小,相比于Bevis公式和GPT2w-1模型,其精度分别提升了31%和46%。
由图4可知,Bevis公式在中国西部地区普遍存在正偏差,且正偏差较高值出现在青藏高原地区的探空站点位处,同时在中国东南部沿海地区存在一定的负偏差;GPT2w-1模型在中国低海拔地区偏差较小,在中国西部尤其是青藏高原等高海拔地区存在较为显著的负偏差;而h0Tm模型在整个中国陆地区域均表现出较小的误差。在RMS方面,Bevis公式和GPT2w-1模型在中国西部和北部部分地区均表现出较大的RMS值,主要受该地区地形起伏变化的影响,而h0Tm模型在中国西部和北部地区RMS值普遍较小。由此可知,在中国区域,尤其是在地形起伏较大的西部地区,使用h0Tm模型相比于Bevis公式和GPT2w-1模型具有较显著的优势。
2.3 青藏高原区域模型精度验证
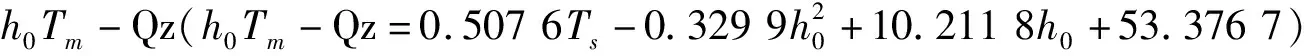
由图5可以看出,Dulan站和Weining站h0Tm-Qz模型的日均bias和日均RMS值明显小于TsTm-Qz模型,4个站点h0Tm-Qz模型的日均bias和日均RMS值普遍低于TsTm-Qz模型的相应误差值。
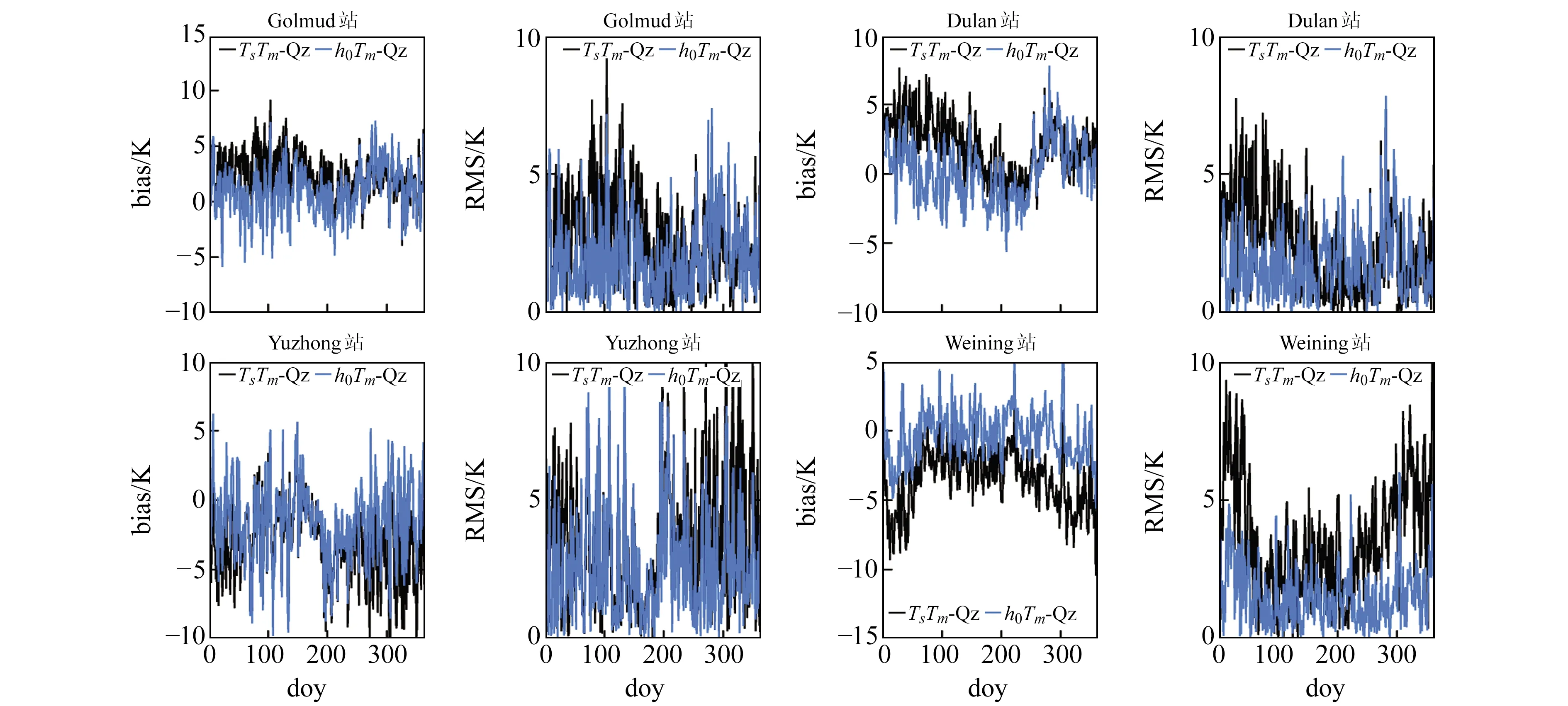
图5 Golmud站、Dulan站、Yuzhong站和Weining站h0Tm-Qz模型与TsTm-Qz模型的日均bias和日均RMS变化值
由表4可知,Bevis公式在青藏高原地区的正偏差最大,TsTm-Qz模型的正负偏差最大值均大于h0Tm-Qz模型,而h0Tm-Qz模型的MAD年均值最小(1.91 K);Bevis公式的RMS平均值最大,为4.87 K;相比于Bevis公式和TsTm-Qz模型,h0Tm-Qz模型的精度分别提高2.50 K(51%)和0.54 K(19%)。由图6可以看出,Bevis公式在青藏高原地区存在显著的正偏差,TsTm-Qz模型的MAD值小于Bevis公式,h0Tm-Qz模型的整体偏差最小;在RMS方面,h0Tm-Qz模型明显优于Bevis公式和TsTm-Qz模型,在青藏高原地区呈现出较高的稳定性和精度。

表4 利用青藏高原地区探空站数据验证h0Tm-Qz模型、TsTm-Qz模型和Bevis公式的精度对比
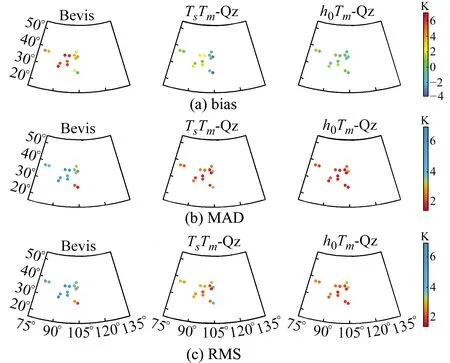
图6 利用2018年青藏高原地区探空站数据检验不同模型的bias、MAD和RMS分布
综上可知,引入变量h0后构成的非线性模型h0Tm在中国区域表现出较高的精度和稳定性,尤其是在青藏高原等地形起伏较大的地区,模型精度明显较优。
3 结 语
本文讨论了区域相对高程h0对加权平均温度的影响,并基于已有的对流层顶经验模型,构建了顾及区域相对高程的中国区域加权平均温度模型h0Tm,同时建立了青藏高原地区的区域模型h0Tm-Qz,通过对比和分析得出如下结论:
1)相比于Bevis公式与GPT2w-1模型,h0Tm模型在中国区域有着更高的精度和稳定性,尤其是在中国西部青藏高原等高海拔地区,模型精度较前两者有显著提升。
2)在青藏高原地区,引入区域相对高程h0后的双因子(h0、Ts)加权平均温度区域模型h0Tm-Qz较单因子(Ts)加权平均温度区域模型TsTm-Qz的误差值小且稳定,说明h0对加权平均温度的垂直改正有重要意义。
3)h0Tm模型中的关键参数h0由对流层顶经验模型计算得到,而该模型只需一个气象参数Ts即可获取相较传统TsTm模型精度更高的Tm信息。因此,h0Tm模型对中国区域高精度GNSS水汽探测具有重要的应用价值,尤其是在中国西部地形起伏较大地区。
致谢:感谢ECMWF中心提供ERA5资料及美国怀俄明大学提供探空资料。

