黄山地震台体应变气压效应分析及修正

李章，李本有，严吉，程文坤，尹天杰，谭笑

(1.安徽省黄山地震台,安徽 黄山 245011；2.安徽省泾县地震台,安徽 泾县 242500；3.安徽省嘉山地震台,安徽 明光 239461)

0 引 言

钻孔体应变观测是地壳应力应变状态及其变化规律的重要研究手段，同时也是现代地震前兆观测手段中不可或缺的技术力量[1-2]。安徽省经过多年的建设和改造，逐步形成了数字化体应变监测网。目前在网运行的体应变仪器有10余套。通过分析历年的观测资料发现，自然环境(降雨、气压、水位等)的快速变化会导致体应变数据产生畸变，是最常见的干扰因素，给地震前兆异常识别带来困难。其中气压畸变通过与大地耦合所产生的短临动力作用对大地形变的影响，成为地壳表面上最重要的快速加卸载源。本文对黄山地震台(以下简称“黄山台”)体应变和气压观测资料进行分析，建立气压干扰的数学公式，从而排除体应变的气压干扰。

通过建立体应变气压效应的修正公式，修正前后效果明显，对观测数据的有效修正有着重要的意义，对干扰识别、捕捉短临地震异常有一定参考意义。

1 观测背景及工作原理

黄山台地处皖南山区屯溪、休宁盆地，近东西向的休宁断裂带和北东向的宁国—绩溪断裂带从台址附近通过，台址岩性为砂岩。钻孔体应变于2009年开始架设观测，孔径130 mm，孔深68.2 m，微风化泥岩。台站应变曲线光滑，固体潮清晰，日变规律较为明显，具有良好的周期性特征(潮汐因子和相对误差分别在0.761、0.041 8左右)。体应变自观测以来，能保持较高的运行率和数据完整率。

钻孔应变仪作为观测地壳应变微小连续变化的前兆观测仪器，不仅能清晰记录到固体潮、地震波、震前异常等重要信息，还能记录到气压、降雨等对地应变场的干扰。仪器的工作原理较为简单，即一个长圆形的弹性筒内，充满了硅油，当它受到四周岩石的挤压或拉伸时，筒内的液体压力发生改变，通过液压的增大或缩小，即可得知岩石的应变状态是压缩还是拉伸。国内外的一些专家通过研究发现，大气压的波动会对地壳形变产生一定的影响，约为10-9量级[3-5]，因此在分析观测资料时很容易将气压干扰误认为是短临异常，掩盖了观测值的真实变化。

2 气压效应分析方法

根据国内外学者研究表明，体应变观测受到多种干扰因素的影响[3-4]，常见的干扰因素按照干扰严重程度排序依次是：自然环境(降雨、气压、水位等)、观测环境以及仪器稳定性。收集整理黄山台体应变和气压观测资料可知，黄山台体应变有很好的趋势变化特征和年变变化特征，而其他分量气压、水位、气温等均只有年变变化特征。气压影响体应变变化可以分为两种类型，一种是像固体潮一样呈现周期性干扰，另一种是无明显特点的非周期性干扰,其中短周期气压扰动对体应变影响比较显著。黄山台体应变受气压干扰，并呈周期性干扰变化(图1)。

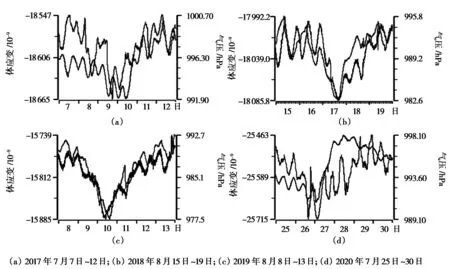
图1 典型气压干扰曲线

2.1 相关分析

气压通过地面载荷导致岩石孔隙压发生变化从而影响体应变观测。具体表现为气压变化在钻孔的垂直方向产生影响，岩体的侧向围压在钻孔的水平方向产生影响。根据弹性力学相关知识，可以简单的从理论上建立出大气压对体应变的影响模型公式[6-7]：

ε=bΔPa

(1)

在这个公式中：ε为钻孔体应变；b为气压影响系数；ΔPa为大气压增量。通过公式分析可知，简单模型下体应变和气压呈正相关性。

另根据实际观测中气压对体应变的影响特征分析发现，气压在短时出现显著大幅扰动时将导致体应变发生同步扰动，而且扰动形态基本一致，扰动时间段基本一致，因此可知二者线性相关性明显。基于此，可以建立气压和体应变观测值之间的一元线性回归方程。

Yt=a+b·Pt

(2)

式中:Yt为体应变观测整点值，Pt为气压观测整点值，b为回归系数，a为常数项。经相关计算得到,a=-23 044.50，b=5.06，相关系数R=0.96。

综合简单理论模型和一元线性回归计算结果，可得气压和体应变二者高度正相关。

2.2 别尔采夫滤波分析

别尔采夫滤波是一种比较简单方便去除潮汐成分的方法，选取黄山台2018年以来整点值观测数据，利用别尔采夫滤波法去除体应变的固体潮和气压的短期变化影响。

设一组等时间序列y(t)=y1+y2+y3+y4+…yi，公式如下：

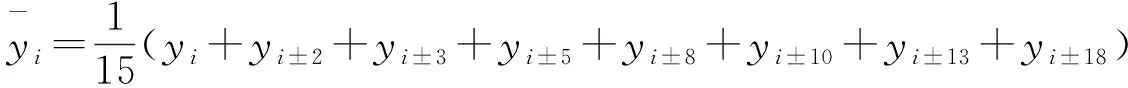
(3)

(4)

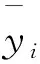
3 气压干扰修正

由上述分析可知，体应变在观测中会受到多种干扰因素的影响，因此为探究气压因素对体应变观测影响，可将其他所有非气压因素归为一类。当体应变与气压出现同步扰动时，可认为此时体应变主要受气压影响，而非气压因素忽略不计。

3.1 长周期气压影响消除

长周期性气压和体应变曲线，在相位上较同步，分析二者相关性：

Yt=a+b·Pt

(5)

Yt为体应变观测值，Pt为气压观测值，a，b为回归数值。代入体应变和气压观测值，即可求得回归值a，b。再将a，b以及气压Pt代回方程中，即可得到一条曲线Y’t，将其从体应变观测值中减去，气压干扰就被去除。Yt-Y’t即为体应变消除长周期气压干扰的残差值。

选取黄山台2017年7月体应变和气压观测数据进行分析，二者的原始数据曲线分别为图2a、b。经过别尔采夫滤波后的体应变和气压分别为图3a、b，消除气压干扰后的体应变为图3c。

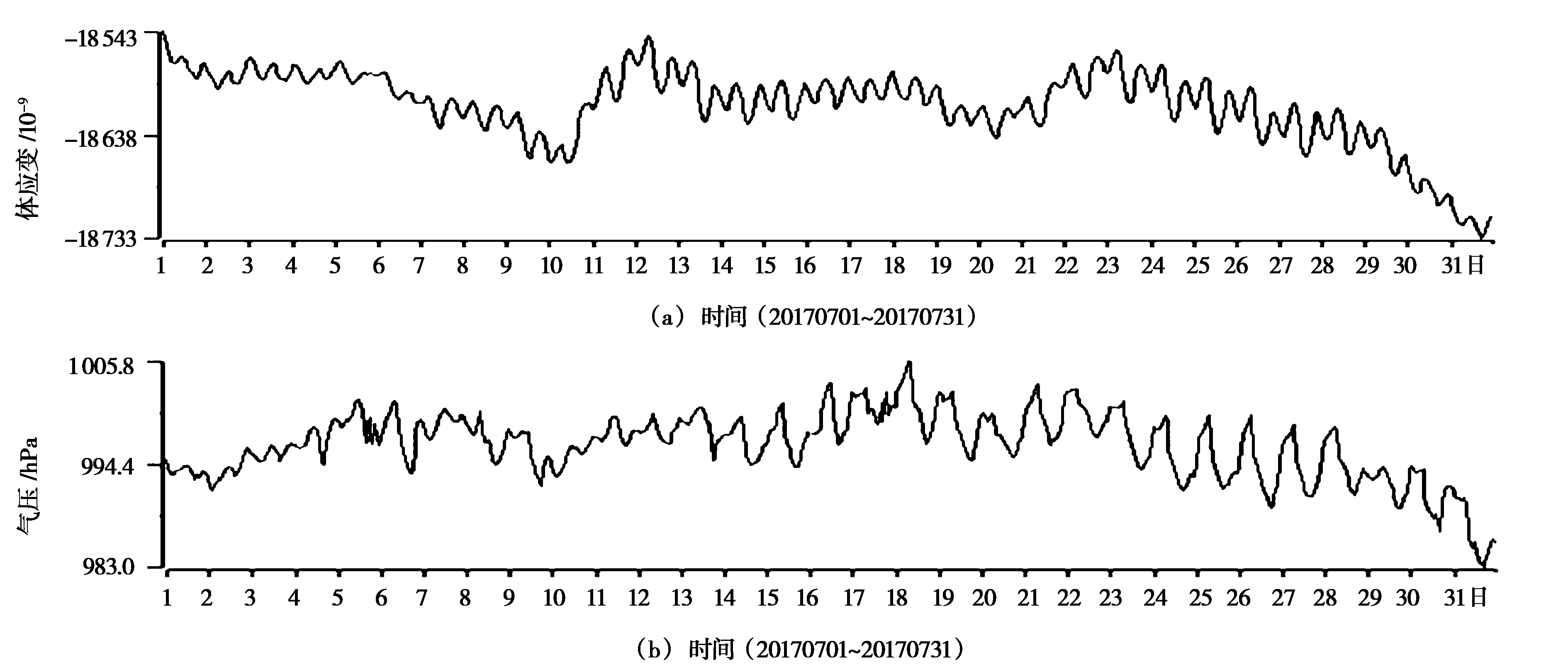
图2 体应变和气压原始曲线

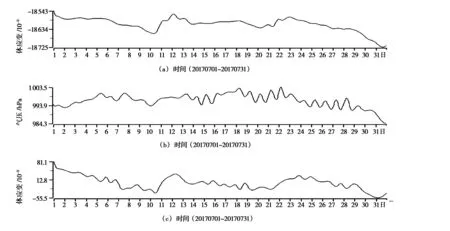
图3 体应变消除气压(长周期)干扰

3.2 短周期气压影响消除

短周期气压对体应变影响较大，同时固体潮汐也影响体应变日变，这里只考虑短时气压干扰。P(t+Δt)为气压，Δt为干扰延时，假设P(t+Δt)=Pt+Δt·P’t，则有：

Yt=a+b·P(t+Δt)，

Yt=a+ b·(Pt+Δt×P’t)

(6)

带入数据，即可求得a，b，再将a，b以及气压Pt带回方程中，即可得到Y’t，将其从体应变观测值中减去，得到残差值，即短期气压干扰就被去除。

选取黄山台2020年7月19日至20日体应变和气压观测数据进行分析，二者的原始数据曲线为图4a、b。经过别尔采夫滤波后的体应变和气压分别为图5a、b，消除气压干扰后的体应变为图5c。

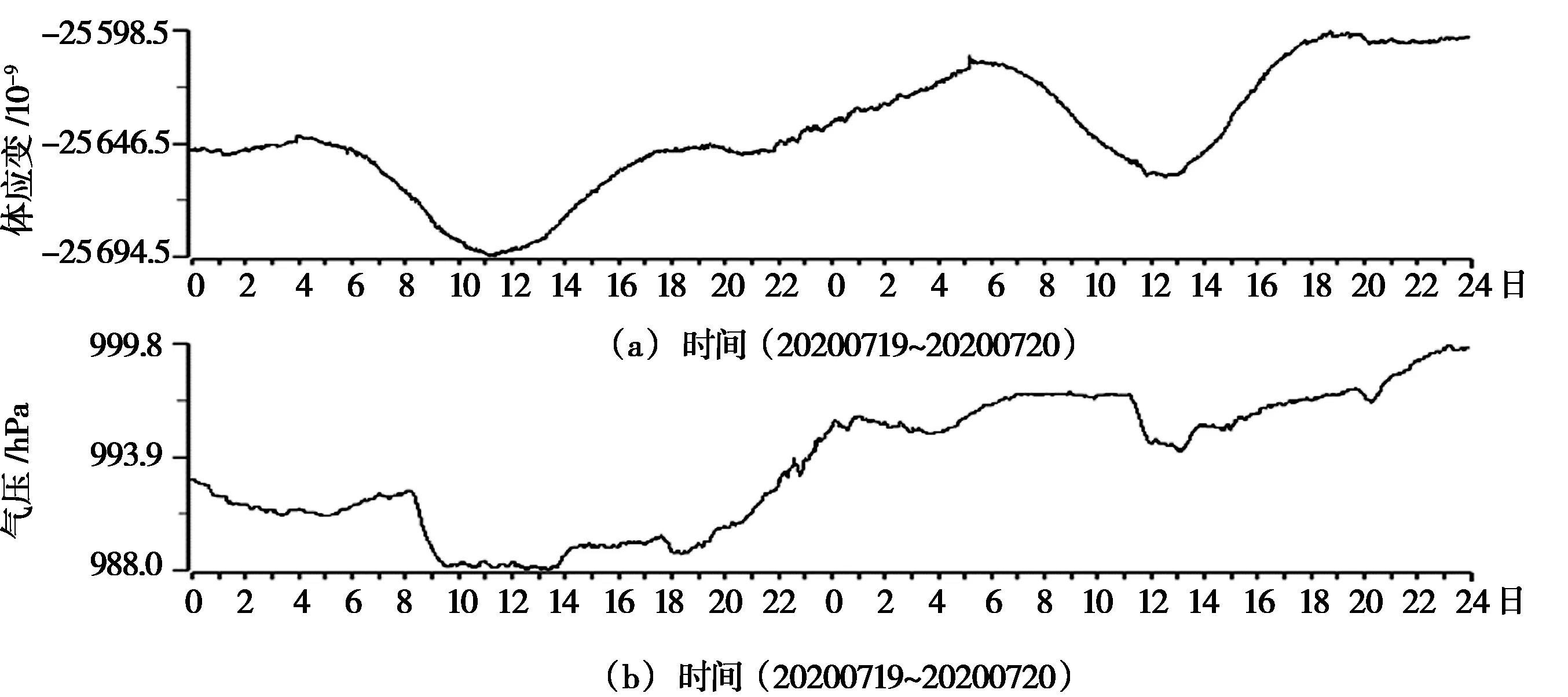
图4 体应变和气压原始曲线

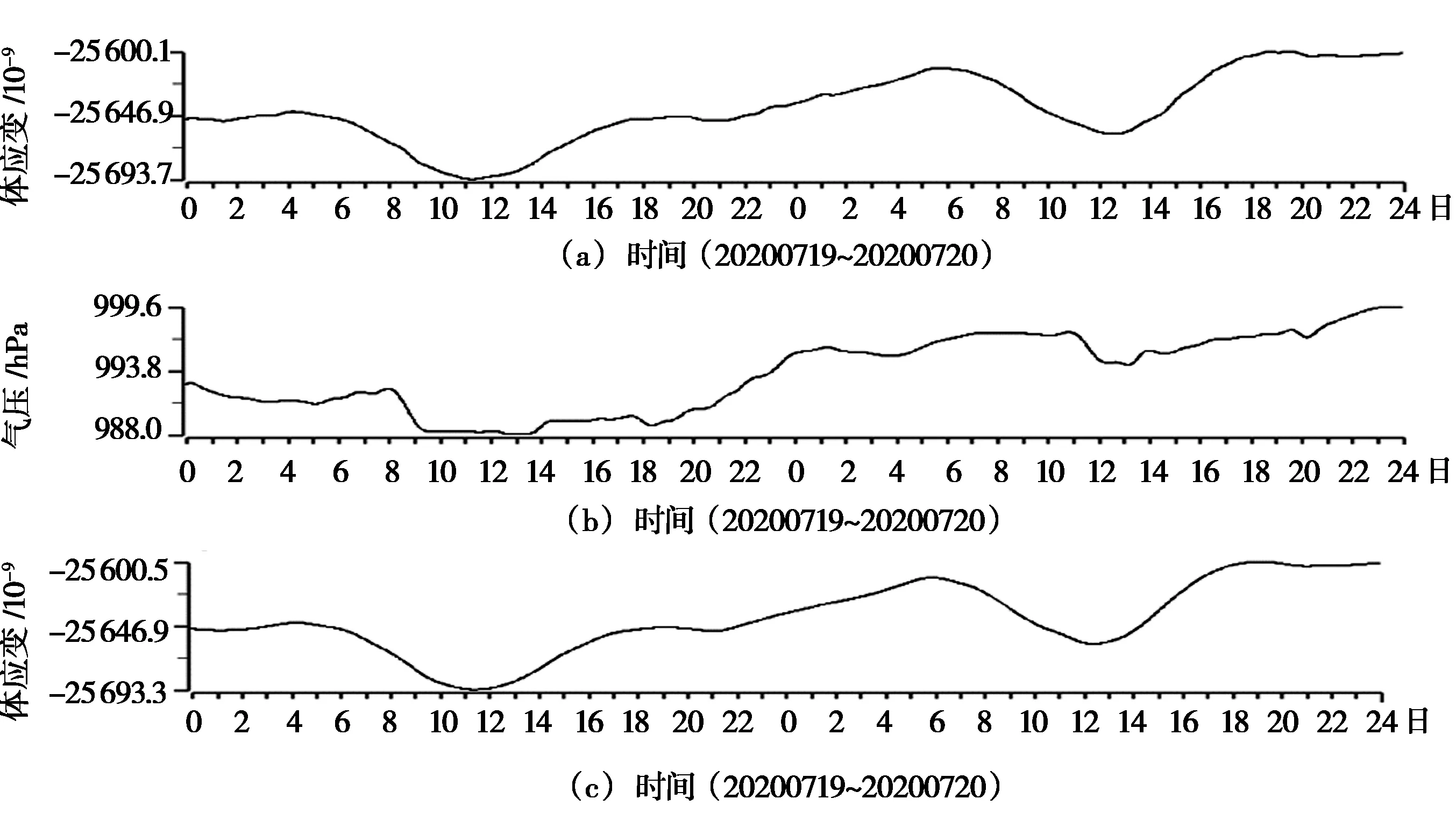
图5 体应变消除气压(短周期)干扰

综合上述，可以看出，经过数学改正后，典型气压干扰得以修正，同步扰动幅度明显减弱甚至消失，曲线形态显著变化。

4 结 论

体应变仪的探头埋于地下一定程度上减小了地表干扰，但由于孔井地质条件，如钻孔岩层裂隙较大、穿过破碎带、气压等因素都会对体应变仪观测造成复杂的影响。对观测数据的有效修正有着重要的意义，对干扰识别、捕捉短临地震异常有一定参考意义。通过对黄山台历年观测资料分析可得结论如下：

(1)黄山台位于皖南山区，且岩性为砂岩，体应变随气压波动而波动，相互间变化形态基本一致。通过计算，二者相关系数达到0.9以上，呈高度正相关，黄山台体应变受气压干扰严重。

(2)通过建立体应变气压效应的修正公式，分别对长周期气压干扰和短周期气压干扰进行修正，修正前后效果明显，同步扰动幅度明显减弱甚至消失，曲线形态更加光滑，说明干扰修正效果显著。