冲击载荷时2A12材料的动态特性及材料本构模型参数识别

杨 全，刘 伟,汤礼军

(航空工业西飞设计院结构强度所，陕西 西安 710089)

1 引 言

航空器在服役和运营过程中，会遭遇到一系列的冲击动力学问题，如飞鸟、碎石等离散源撞击等[1]。结构在瞬变、动载荷作用下的运动、变形和破坏规律越来越受重视。在结构动响应的研究中，离不开材料动态力学性能的研究。常用于研究材料动态力学性能的装置有万能材料试验机、高速液压伺服材料试验机和霍普金森杆装置等。其中，霍普金森杆装置主要针对应变率在400/s以下的试验，其优势在于试验成本低，重复性好，测试手段简单[2]，在材料动态拉伸试验中应用较广。

在冲击动力学数值研究分析中，选择材料模式以及材料参数的合理性将决定结果的准确度。为此，人们提出了多种本构模型来描述金属材料与应变率相关的应力-应变响应。工程中常用理想弹性模型、理想弹塑性模型和弹塑性模型来模拟材料的力学特性[3]，评估结构动态力学特性。其中，弹塑性材料模型以Johnson-Cook模型(J-C模型)应用较为广泛。在主流的动力学分析软件(如ABAQUS，MSC.Dytran，LS-dyna等)中，均含有此材料模型。

本文以航空常用的2A12铝合金材料为对象，开展物理冲击试验，获取材料在不同冲击载荷下的应力-应变数据。采用有限元技术并结合材料的动态试验力学性能数据识别Johnson-Cook模型参数，建立宽应变率范围下材料的动态本构关系，实现了材料与相关力学性能的完整表达。

2 材料冲击试验

材料动态拉伸试验在中国科技大学的摆锤式杆-杆型冲击拉伸试验装置上进行，试验装置简图如图1所示。试验件材料为2A12铝合金，尺寸为62mm×14mm×3mm。夹持段与试验段通过几何尺度渐变过渡，各段的具体尺寸见图2。

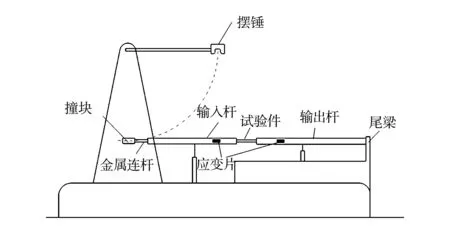
图1 摆锤式杆-杆型冲击拉伸试验装置简图

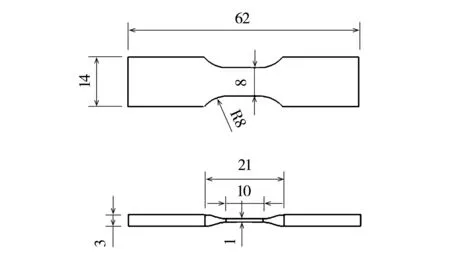
图2 试验件几何尺寸

试验中，当摆锤式旋转盘的锤头以一定速度撞击撞块时，撞块向前运动拉断金属短杆(由铝合金制成)，在输入杆中产生拉伸应力脉冲。这个应力脉冲沿输入杆传播通过试件，一部分透射到输出杆中，一部分反射回到输入杆中。根据一维应力波的理论，并假定试件中应力是均匀的，可得到试件的应力、应变和应变率的计算公式[4]：

(1)

其中，L0，A0为试件的初始长度和横截面面积，C0，E，As为输入杆和输出杆的弹性波速、弹性模量和横截面面积，εi，εt为输入杆和输出杆上应变片测量得到的入射波和透射波产生的应变。

3 有限元模型

有限元模型相对试验模型进行了简化，由试验件、撞块和撞锤组成，见图3。试验件与撞块共节点，形成一个整体。撞锤为带内孔的方形体，撞锤穿过试验件，可按给定的水平运动速度撞击撞块。试验件、撞块和撞锤均采用六面体单元进行离散，使用MSC.Dytran软件中的刚性材料刚体MAIGRIG对撞锤赋予刚性材料属性，试验件和撞块的材料属性采用J-C模型来定义。

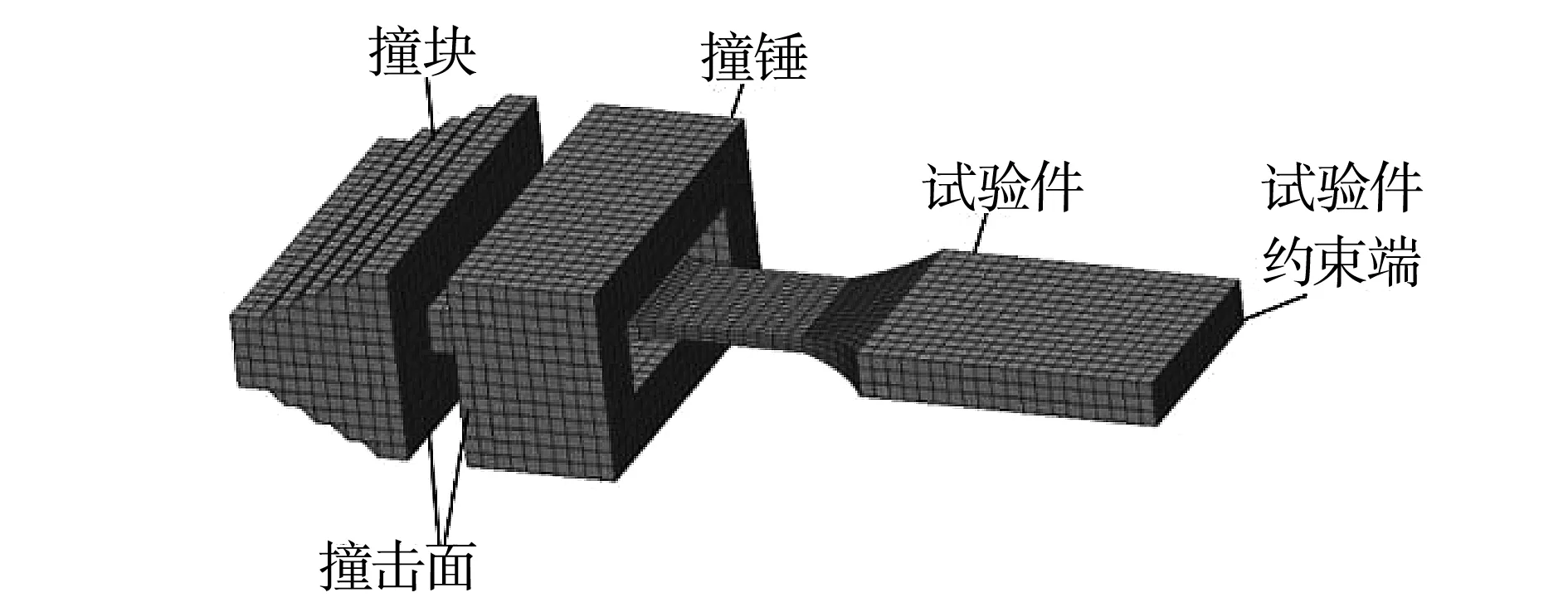
图3 有限元模型

在撞锤与撞块两者接触面间定义接触关系，接触面间的穿透检查容差设为0.01mm，防止穿透量过大使两物体间产生很大的相互作用力[3]。另外，撞锤在撞击撞块后由于试验件的反作用力使撞块尽早脱离试验件，以避免二次撞击给试验件自身内部应力波造成反射振荡。试验件网格尺寸与分析时间步长通过材料的应力波跨越网格中最小元素的时间来协调确定。

4 材料本构方程及参数识别

4.1 材料本构方程

采用有限元技术模拟材料动态冲击试验时，材料模型选用J-C模型。J-C模型是基于多种材料冲击试验数据总结而得出的黏塑性经验公式，由应变硬化、应变率效应、热软化效应组成。因其参数少、使用方便等特点，在工程计算中得到了广泛应用，方程式如下[5]：

(2)

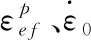
(3)

4.2 确定本构方程参数

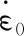
表1 不同应变率下的极限应力值

表1 不同应变率下的极限应力值

表2 J-C模型参数

相对误差平均值公式为：

(4)

式中，Si和Ti分别为计算值与试验值，m为塑性区内所取样本点数。利用式(4)计算的结果见表3，满足工程技术要求。

表3 拟合误差的平均值

不同应变率下的应力-应变曲线如图4-图6所示。由图可以看出，在3种不同应变率下计算得出的应力-应变曲线与试验所得应力-应变曲线相吻合，所取J-C模型参数值能很好地反映材料2A12的力学性能。

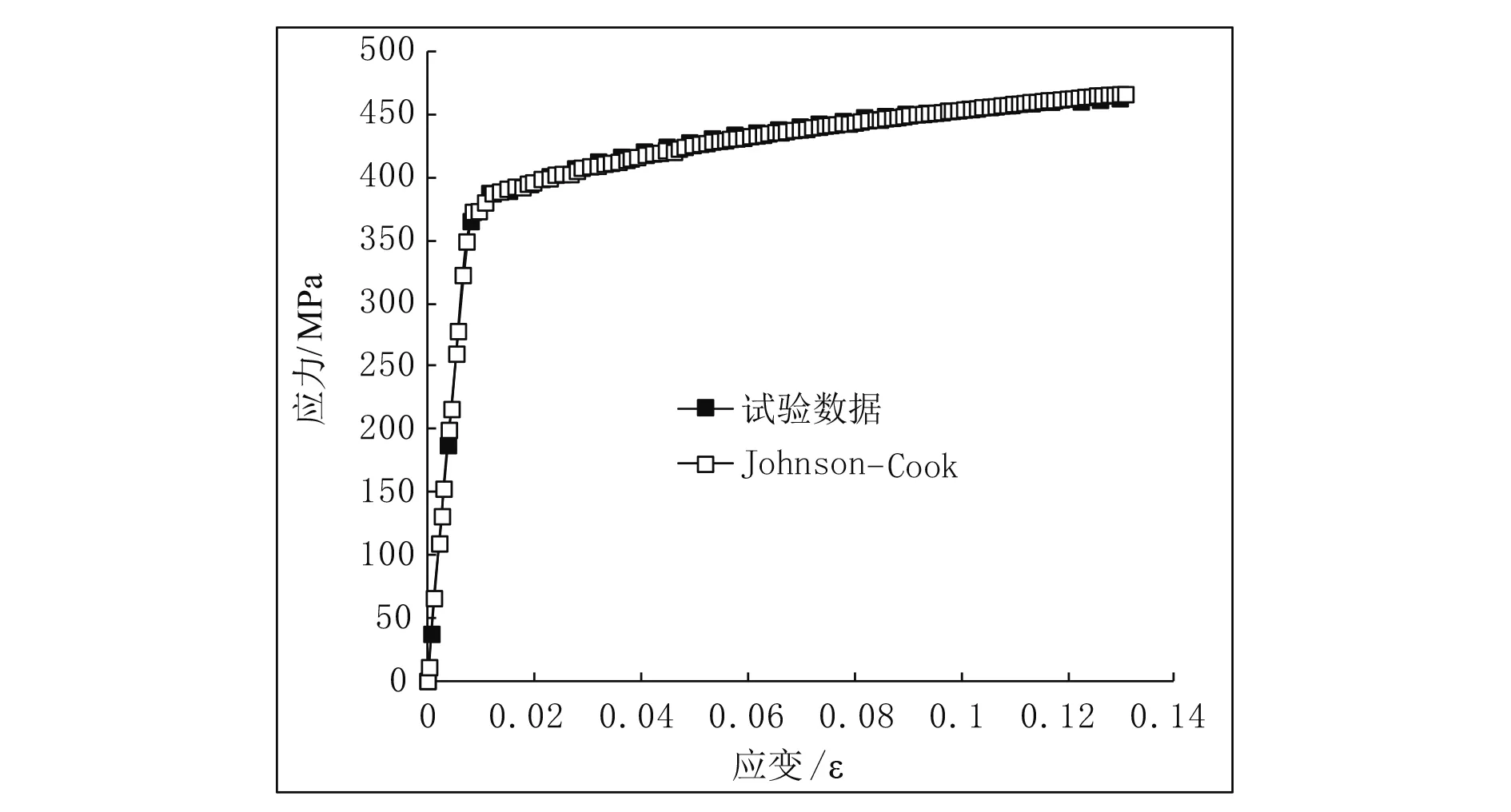
图4 应力-应变曲线

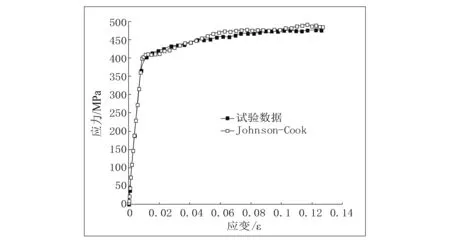
图5 应力-应变曲线

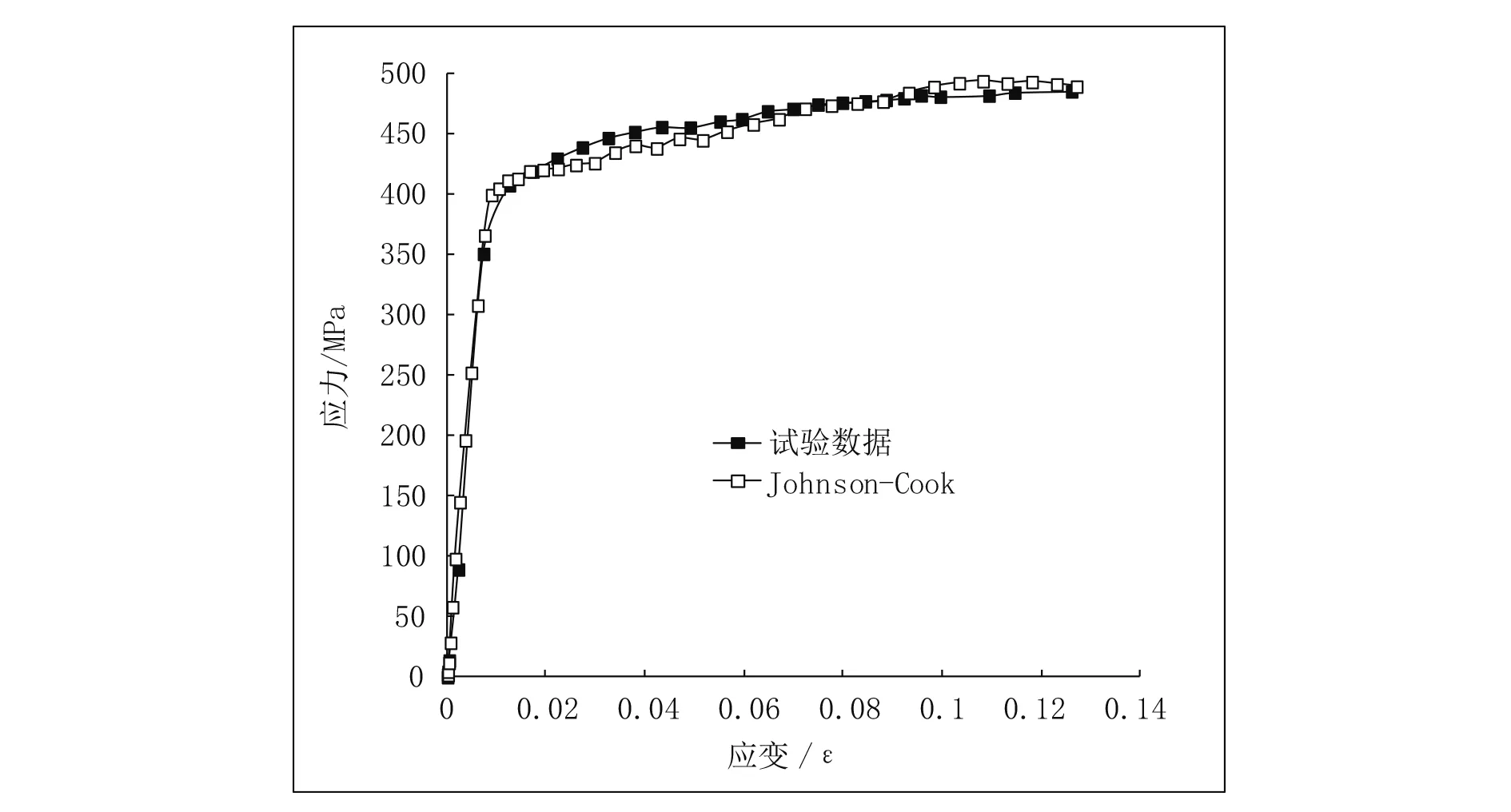
图6 应力-应变曲线

5 结 论

根据材料冲击试验数据分析得出，2A12在应变率为330/s以下，材料力学性能对应变率不敏感。通过限元仿真分析，采用J-C模型能较好地模拟材料在宽应变率范围下的力学动态特性，在获取相关模型参数后能较完整地实现材料与相关力学性能的表达。