基于DEM 模拟的颗粒材料热固结试验分析*

应涛涛，魏良针，杨 磊，夏念兴，龚礼岳

（1.温州市铁路与轨道交通投资集团有限公司，浙江 温州 325000；2.温州大学 建筑工程学院，浙江 温州 325000）

基于节能环保可持续的发展原则，如能源桩[1]和地源热泵[2]等与温度相关的能源工程[3-5]开展得越来越多，温度对能源结构周边土体的影响已经成为工程在使用过程中不可忽略的重要因素。Sang 等[6]分别在室内和高温下进行了饱和粘土的热排水固结试验，发现温度可以加快排水固结的固结速度。Xiong 等[7]开发了一种温度控制的三轴试验装置，研究了饱和软粉质粘土在不同温度下的动态不排水特征，发现温度对软粘土的累积塑性变形、孔隙水压力等特性有很大的影响。此外，温度土体的强度[8-10]、空隙特征[11]、变形[12]等特性也有较大的影响。土体特性的改变必然会造成土体与结构接触面特性的变化。Maghsoodi 等[13]建立了非等温土-结构界面模型，讨论了温度对粘土-结构界面空隙率的影响。Donna 等[14]开发了一种直接剪切装置，研究了不同温度下桩-土界面的响应，发现粘土-混凝土界面的强度随温度的升高而增加。此外，研究还表明温度对土-结构界面的接触力[15]、应力-应变[16]和抗剪强度[17-19]等特性都有影响。而土-结构接触面特性的变化势必会引起结构的不均匀沉降甚至失稳，所以需进一步深入土体的温度效应的研究。但是，上述试验中都只是分析了温度对土体在宏观上的如强度、应力和应变等影响，缺少了如各项异性、内部接触力分布等微观层面的研究。

离散元法[20]（DEM）作为一种能应用于工程领域的数值计算方法，将岩体视为不连续的离散块体能有效地进行颗粒接触间的微观模拟。Pan 等[21]通过离散元模拟了粗粒土的热诱导变形，发现粗粒土在加热时发生膨胀，在冷却时发生收缩，且收缩的幅度大于膨胀的幅度；同时还发现了由于颗粒间的滑动，颗粒重排的增加。Coulibaly 等[22]通过离散元法对粒状材料进行了热循环的模拟，发现了温度循环对颗粒材料的结构和性能都有显著的影响。Zhao 等[23]则发现热循环在粒状材料内部会引起显著的应力松弛。但是，目前离散元法进行的热力耦合模拟大多采用的是颗粒体体积膨胀法，较少对真实传热过程的模拟。

所以，本文分别采用热传递法和颗粒体积膨胀法，通过离散元软件PFC2D来模拟单次温度循环下的热固结实验。宏观上分析试样密实化和应力衰减的规律，在微观方面研究了颗粒间接触的各项异性受温度的影响规律，最后对比分析了两种模拟方法在模拟过程中的同异性。

1 热力耦合模型的机理

1.1 颗粒体积膨胀法

颗粒体积膨胀法是指不考虑颗粒间的热能传递，颗粒温度的变化直接通过参数的设置来实现。在模拟过程中，通过公式（1）实现温度对颗粒体积的影响。

式中，ΔT 是颗粒温度的变化量；α 是颗粒的热膨胀系数；R0是颗粒变温前的半径；ΔR 是颗粒在变温时产生的半径的变化量。

颗粒体积的改变使颗粒间接触的重叠量δn随之发生变化，然后通过接触力的计算公式（2）实现热力耦合的模拟。

在采用颗粒体积膨胀法的温度固结试验模拟过程中，全部颗粒的温度都是相同的，且都是统一发生变化的。由于不需要考虑温度的传递，采用颗粒体积膨胀法的热力耦合在PFC2D软件上的模拟更加快速。因此在进行如温度循环试验这类温度需要长期持续变化的模拟中颗粒体积膨胀法的运用是必不可少的。

1.2 热传递法

在采用热传递法的热力耦合模型中，每一个颗粒都代表一个蓄热池。在两个蓄热池颗粒互相接触后，中心会形成一根连接这两个蓄热池的传热管道简称热管。通过热管就可以实现热能在两个蓄热池之间的转移。

在模拟过程中，将边界墙体作为恒定的热源对内部的颗粒进行热能的供应。且边界墙体不随温度的变化而产生变形。在传热过程中，边界墙体的热能会从较近的颗粒向较远的颗粒传输。而颗粒的温度在边界热能的作用下会不断升高直到与边界墙体的温度相同。与此同时，在颗粒温度升高的过程中，颗粒体积则会根据公式（1）产生膨胀。并通过公式（2）实现温度对试样力学性质的影响。

通过热传递法进行的热力耦合模拟更加接近现实中能源结构对周边土体的影响。但是由于其在模拟过程中需要兼顾热传递和力学计算，会导致模拟速度的降低，不利于开展如多周期温度循环固结试验等有长时间传热试验的模拟。

2 模型的建立及模拟方案

2.1 数值模型的建立

图1 为试样模型的颗粒粒径分布曲线，曲线中的相关数据见表1。按照这一级配曲线，生成相对密实度Dr为0.2 的松散试样其对应的孔隙比为0.2376。

图1 颗粒级配曲线

模型中力学参数和热力学参数的选取主要参考石英砂的数值如表2 所示。

在颗粒生成后，循环计算至试样内部平均不平衡系数αf（见公式（3））小于1e-5。将平衡后的试样进行侧限压缩固结。在固结过程中的边界条件为在上下墙体施加100kPa 的恒定荷载，左右墙体保持静止不动。在后续的温度固结试验过程中会保持这个边界条件不变。侧向固结后的试样如图2 所示，此时试样的孔隙比e0为0.2312，将此状态下的试样视为温度固结试验中的初始状态。

图2 数值试样模型

式中N 是颗粒的总数；C 是总的接触数量；Ci是第i 个颗粒的接触数量；F(ij)是第i 个颗粒的第j 个接触的接触力；Fb(i)是第i 个颗粒的体积力；Fc(i)是第i 个接触的接触力。

2.2 模拟方案

分别采用热传递法和颗粒体积膨胀法进行温度固结试验的模拟。在模拟过程中，设置颗粒的初始温度T0为20℃，温度变化过程为20℃～60℃～20℃。

在热传递法中，先将边界墙体的温度设置为60℃并保持温度固定，在试样的平均温度升高到60℃后再将边界墙体的温度改为20℃，使试样的平均温度重新降低到20℃，以此实现温度循环固结试验的模拟。

在颗粒体积膨胀法中，以固定的温度增量ΔT=1℃进行颗粒温度的设置。试样平均温度具体的变化过程为20℃～21℃～22℃～......～60℃～59℃～58℃～......～20℃，如图3所示。

图3 温度变化示意图

最后，将两种热力耦合方法的模拟数据在宏观角度（孔隙比、侧向应力）和微观角度（各项异性）上进行对比分析。

3 试验结果

3.1 孔隙比及侧向应力

为方便在数据图中进行标注，将热传递法简称为方法Ⅰ，将颗粒体积膨胀法简称为方法Ⅱ。图4 为两种方法下的孔隙比在温度循环固结模拟下的对比结果。当温度从20℃升高到60℃时，两种方法分别从初始孔隙比0.23122降低到了0.23082 和0.23081，当温度从60℃降低到20℃时，孔隙比又分别升高到了0.23114 和0.23117。可以看出，在经过一次温度循环后，试样的孔隙比相较于初始状态时是降低的。这是由于在恒定的边界条件作用下，温度的升高使颗粒的体积不断膨胀降低了试样的孔隙比，而温度的降低使颗粒体积逐渐收缩，导致试样孔隙比的增加，颗粒体积在不断变化过程中产生了塑性变形，使试样体积无法还原到初始状态。这种孔隙比的变化规律与Liu 等[30]关于不同温度下的孔隙率变化规律相同。同时也可以看出，两种热力耦合方法在孔隙比上的变化是高度吻合的。

图4 孔隙比在温度循环过程中的变化

由于在边界条件中上下墙体施加了恒定的荷载，试样在竖直方向上的应力是恒定的，因此对于应力的研究主要针对侧向应力。图5 为试样的侧向应力在热固结试验模拟中的变化情况。随着温度的升高，侧向应力从初始应力41.54kPa 分别增加到了48.34kPa 和48.11kPa。随着温度的降低，侧向应力也随之降低到了40.44kPa 和40.59kPa。这也是由于侧向墙体对试样的约束力会随着颗粒体积的膨胀而增加，随着颗粒体积的收缩而降低的原因造成的。此外，可以看出模型Ⅰ与模型Ⅱ的侧向应力曲线十分相近的。

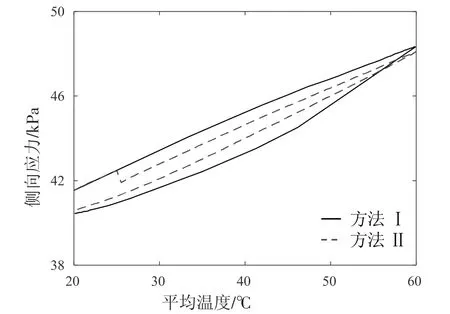
图5 温度循环过程中侧围压力的变化

3.2 各项异性

参考Rothenburg 和Bathurst[31]关于各向异性的拟合公式（4）分别从法向接触力和切向接触力两个方面对比方法Ⅰ和方法Ⅱ对试样的影响。

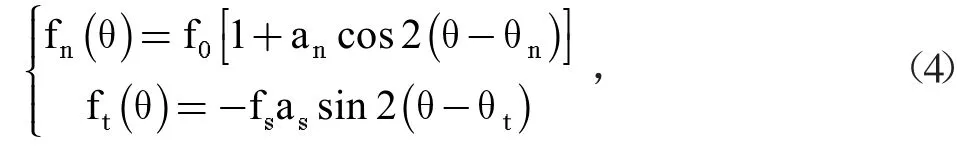
式中：fn和ft分别为法向接触力和切向接触力在θ（θ∈[0，2π]）角度上的大小；f0和fs为法向接触力和切向接触力的平均值；an和as分别表示了法向接触力和切向接触力的方向变化量，其数值越大，接触力的各向异性就越明显，由公式（5）计算所得；θn为最大平均法向接触力的倾角；θt为平均切应力为零时的倾角。

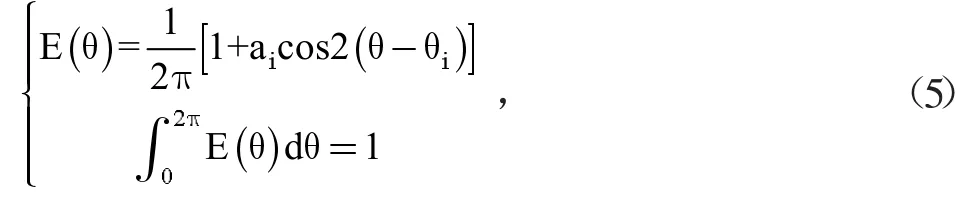
式中：E（θ）为接触密度函数；ai表示分布的各向异性大小；θi表示i 对应的各向异性方向，其中i 分别为n 和t。

图6 为温度固结试验模拟中平均法向接触力随温度的变化曲线。当温度从20℃升高到60℃时，方法Ⅰ和方法Ⅱ的f0从65.26kN 分别增加到了69.86kN 和70.06kN。当试样的温度重新降低到20℃时，f0又分别降低到了65.02kN 和65.05kN。相较于初始状态分别降低了0.24kN和0.21kN。

为了进一步观察法向接触力在试样内部的分布情况，分别取平均温度为60℃和完成温度循环后（平均温度为20℃）的试样进行分析，如图7 所示。当平均温度分别为60℃和20℃时，法向接触力在水平方向上的分布分别约为64.72kN 和52.51kN，在竖直方向上的分布则因为稳定的边界条件保持在76.49kN 左右。当试样的平均温度重新降低到20℃时，由于法向接触力在水平方向上的分布降低，使其整体处于降低的趋势，与图6 中的变化趋势相同。此外，可以看出，热传递法和颗粒体积膨胀法在相同温度下的法向接触力的分布高度吻合。

图6 平均法向接触力随温度的变化

图7 法向接触力分布示意图

图8 为平均切向接触力fs在热固结试验模拟中的变化曲线。从图中可以看出，随着温度的升高，两种方法的平均切向接触力fs从初始的1.735kN 分别降低到了0.637kN 和0.631kN。随着温度的降低，fs分别增加到了1.883kN 和1.855kN。相较于初始状态，经过温度循环后的试样的切向接触力是有所增加的。

图8 平均切向接触力随温度的变化

如图9 所示，分析了切向接触力在平均温度分别为20℃和60℃时的分布。当试样的平均温度从60℃降低到20℃时，切向接触力在方向上分布的最大值从0.4635kN增加到了2.837kN，变化情况与图8 中的曲线相吻合。同时，当平均温度为60℃时，方法Ⅰ和方法Ⅱ的切向接触力方向上的最大值分别为0.4635kN 和0.4237kN，其差异可以忽略不计。因此，两种方法在切向接触力的分布上也有高度的相似性。

图9 平均切向接触力分布示意图

4 结论

为了进一步研究在能源桩的使用过程中，桩身温度的变化对其周边土体的影响。本文通过PFC2D软件，利用离散元法（DEM），分别采用热传递法和颗粒体积膨胀法对石英砂材料进行了热固结试验的模拟。分别从宏观角度和微观角度分析了结构接触面周围土壤的热耦合力学性能。并对比分析了两种热力耦合方法的模拟情况。得到以下结论：

（1）通过PFC2D软件，利用离散元法，无论是基于热传递法还是颗粒体积膨胀法，都能很好地实现温度固结试验的模拟，在模拟过程中，能够明显地体现出温度对颗粒体积的影响。

（2）在宏观角度上，在上下墙体施加稳定100kPa 的荷载，左右墙体保持固定的边界下，在温度循环固结试验模拟中，颗粒体积产生塑性变形导致孔隙比的降低，试样变化更加密实；因此也导致了试样侧向应力的降低。

（3）在微观角度上，由于在水平方向的分布随侧向应力的降低而降低，法向接触力在经过温度循环后是降低的。与之完全相反的是平均切向接触力是增加的。

（4）热传递法和颗粒体积膨胀法在循环的热固结试验中的模拟结果无论是在宏观方面还是在微观方面，都具有高度的一致性。

以上研究结果可为能源桩周土的研究提供参考依据。