改进NSGA-Ⅱ的多区域可用输电容量协调决策

江建 左宏基 熊化化 李书强 付国

摘 要：在电力市场环境下，合理计算可用输电容量，可以保障交易双方的经济利益。非支配排序精英遗传算法（NSGA-II）在求解多目标优化问题时易早熟，收敛性能差，文中对其进行改进，构建多种群以增强种群之间的竞争优势，并采用多交叉算子交替迭代以增强最优解集中个体的局部搜索能力，使其快速收敛于最优解，为了使多种群中的优势个体更多保留下来，自动调整子种群规模。以国内某地区至省内区域和省外区域的可用输电能力协调优化为例，采用改进后的NSGA-II算法所得结果与NSGA-II算法相比收敛性能优越和求解结果更加合理。

关键词：多区域ATC;协调优化;改进的 NSGA-II

DOI：10.15938/j.jhust.2021.04.006

中图分类号：TM744

文献标志码：A

文章编号：1007-2683（2021）04-0038-08

Abstract：In electricity market environment， reasonable calculation of available transmission capacity can protect the economic interests of both parties. In order to solve the multi-objective optimization problem， the non-dominated sorting genetic algorithm（NSGA-II） is premature and has poor convergence performance. In this paper， it is improved to build a variety of groups to enhance the competitive advantage between the populations， and the multi-crossing operators are used to iterate alternately to enhance the local search ability of the individuals in the optimal solution concentration， so that they can converge to the optimal solution quickly. In order to keep more dominant individuals in various groups， the sub-population size is adjusted automatically. Taking the ATC coordination optimization from a certain region in China to the region in and out of the province as an example， the result of the improved NSGA-II algorithm is superior to that of NSGA-II algorithm in convergence performance and more reasonable solution results.

Keywords：multi region ATC; coordinated optimization; improved NSGA-II

0 引 言

可用输电能力（available transfer capability，ATC）表示为电力系统中可用于商业交易的输电容量[1]。后文中出现的可用输电能力采用ATC表示，准确计算可用输电容量可以保障电力市场交易中各方的经济利益。

传统ATC求解时考虑的都是确定性方法，往往过高估计了输电可靠性裕度，使所得的结果偏于保守[2]。因此，对ATC求解时，需要考虑系统中各种不确定性因素的影响并构建其概率模型[3]，使所得结果能够反映各种随机因素的影响，为电网的规划运行提供更接近真实值的数据指标。当前针对电力系统中各种不确定性因素的研究主要有如下兩类方法，其一，将各种不确定性因素视为随机变量，借助概率统计方法得到ATC的概率分布和统计特征[4-6]，ATC的概率求解有使用蒙特卡洛仿真[7]和采用多项式混沌展开以近似表达复杂的概率特征[8]两种形式;其二，机会约束规划法，需要已知随机变量的概率分布，在求解时将其转换为等价的确定性约束条件[9]。

利用以上方法得到的ATC只能反映一个区域的情况。近年来，国家电网公司开始实施电网互联以较少的备用实现较高的可靠性，所以需要考虑多个区域ATC同步输送问题[10-11]，多区域ATC之间存在相互制约，通过构造多目标优化模型可以协调调度各区域的输电容量。

目前NSGA-Ⅱ算法广泛应用在多目标优化问题求解中，但是由于其单种群遗传操作，导致在求解过程中收敛性能低和优化目标易早熟 [12]。文[13]为了提高可行域的多样性，将不可行域进行分类并在其中找到一个参考点，以此扩大了可行域的范围，增大了种群的多样性;文[14]采用参考点的方法替代传统算法的非支配排序以保持进化过程最优解的多样性并引进重力搜索算法加快收敛。以上文献对NSGA-II算法进行了不同方向的更新，并提高了传统优化方法的效果，但是单一种群和单一交叉算子使局部搜索最优解的本质没有改变。

本文参考文[15]构建的多区域ATC的协调优化模型，对该文献所采用的NSGA-II求解算法进行改进，构建多种群增强种群之间的竞争力，并采用多交叉算子交替迭代以增强最优解集中个体的局部搜索能力，使其快速收敛于最优解，为了使子种群中的优势个体更多保留下来，在保证种群总体数量不变的情况下，自动调整子种群规模，最后以国内某地区至省内区域和省外区域的ATC协调优化算例中验证了改进NSGA-II的有效性。

1 多区域可用输电容量协调优化模型

1.1 单一区域可用输电容量决策模型

本文参考文[15]，考虑电力系统各种不确定因素的干扰，以最大收益为目标构建ATC决策模型。

式中：Ti是区域i的ATC;Wi（Ti）为区域i向其他区域提供输电服务的风险收益;Bi（Ti）为区域i向其他区域提供输电服务的收益;Ci（Ti）当ATC的决策量为Ti时由于不确定性因素的影响使其不能达到规定的输送容量时的损失;λATCi和βi为对区域i的单位输电服务价格以及中断输电时的赔偿费用;P（k）是状态k发生的概率;Ti（k）是区域i在状态k下的ATC;S表示Ti（k）不大于Ti的系统状态集合。

约束条件主要考虑网络安全约束和发电机出力约束，具体约束条件可查阅文[15]。

1.2 多区域可用输电容量协调优化模型

电网互联背景下，仅求解单一区域的ATC，不能反映目前复杂电力系统间多区域电力传输问题，因此，本文在单一区域可用输电容量决策模型的基础上，考虑多区域之间协同优化，以1.1节所示的单一区域收益函数为优化子目标，构建风险收益总和最大的多区域可用输电容量协调优化模型如下式所示：

式中：m为待优化区域的数量，[W1，W2，W3，…，Wm]T为m个子区域可用输电容量决策的风险收益组成的优化向量，Wm为区域m向其他区域提供输电服务的风险收益。

约束条件如下：

1）潮流约束。

2）发电机出力约束：

3）风电场出力约束：

4）节点电压约束：

式中：Vmini和Vmaxi分别为节点i电压幅值的上下限;N为各区域总节点数。

5）支路有功功率约束：

2 ATC的概率分布

2.1 系统不确定因素的处理

为了获得概率ATC，需要将电网中各种不确定性因素使用概率模型表示，其中，各节点负荷波动情况服从ΔS～N（μS，i，σS，i），各元件的随机启停状态服从下式：

式中，Xq为元件q的状态。

对研究区域内风速进行模拟，可以发现其符合Weibull分布，因此本文风电功率的不确定性采用Weibull分布来表示：

式中：k为形状系数;c为尺度参数。

单一风电场输出功率和风速的关系如下：

2.2 三点估计法求解ATC的概率分布

在求解各个区域ATC的概率分布时，目前最常用的有蒙特卡洛仿真和点估计法，由于蒙特卡洛仿真技术需要大量的仿真，耗时较长，并且电网中的不确定因素主要是负荷波动、元件随机停运和风电场出力不确定性，其模型的概率分布比较简单，因此本文采用三点估计法求解ATC的概率分布。

三点估计法基本原理是对于有N维随机变量的函数，只需在每个随机变量取3个点，即3×N次确定性计算即可得到所需的概率分布，具体的三点估计原理可参考文[16]，利用三点估计求解各个区域ATC的概率分布步骤如下：

1）根据电力系统各元件的随机启停概率分布P（Xq=xj）和负荷波动分布ΔS～N（μS，i，σS，i）以及风电场的输出功率PWi，确定三类不确定因素的四阶矩。

2）在每一个变量ΔSi、Xq、PWi处，取3个估计点，即选取每个变量的均值点和左、右邻域内的两个点，并计算每个点对应的权重系数。

3）假设该电力系统有N个节点，M个输电元件，K个风电场，需要进行3（M+N+K）次确定性最优潮流计算，当每个随机变量都取均值点时，只需要进行一次计算，所以最终只需进行2（M+N+K）+1次潮流计算，便能获得每个区域的ATC概率密度分布fpd。

3 改进非支配排序精英遗传算法

由于目前的NSGA-Ⅱ算法采取单种群遗传操作，容易出现早熟现象且收敛性低等问题，本文对NSGA-Ⅱ进行改进，采用多种群遗传操作增强种群之间的竞争力保留更多优势个体，多交叉算子提高局部搜索能力，自适应调整种群规模避免过早成熟。将改进后的NSGA-Ⅱ算法应用在多区域ATC协调优化决策中具有较好的效果。下图1为改进的NSGA-Ⅱ算法的操作过程。

3.1 多種群构建与EXS解集初始化

为了增强种群中个体的多样性，将传统NSGA-Ⅱ中的单一种群，随机划分为两个子种群，每个子种群使用一个不同的交叉算子，从而增强其收敛性能。

由于不同的交叉算子决定了子代个体的性能，因此，对每个种群分配一个独特的交叉算子以保证不同种群间个体的多样性。其中，交叉算子SBX[17]（the simulated binary crossover）可以从2个父代中交叉出任意子代，子代个体逼近父代，具有较好的局部寻优能力。交叉算子SPX[18]（the simplex crossover）从生成的2个子代中选择最好的那个作为最后的子代，能够协调好种群的开发和探索性能，善于求解多模态函数。

以SBX为例模拟EXS解集个体间的交叉操作过程，其中，Q1，i、Q2，i为父代通过交叉产生的子代个体，参数α通过式（14）生成，β为（0，1）之间的任意随机数。

种群的初始状态直接影响优化结果的准确性，EXS解集的初始化过程如下：

1）将种群平均分为2个个体数为NP/2的子种群;

2）各子种群内部分别进行遗传操作产生子代Q1，i、Q2，i;

3）父代和子代合并后的子种群中进行非劣排序得到R1，i;

4）选择每个子种群中的优势个体，即前l层作为EXS解集中的初始化个体。

3.2 外部最优解集的更新过程

最优解的收敛速度是评价多目标优化算法的一个性能指标，为了使EXS解集中的个体逼近所求目标的实际最优解，在每次迭代过程保留更多优势个体的种群，采用不同的交叉算子对EXS解集的交替迭代更新，以保证其快速收敛至全局最优解。

EXS解集间的迭代更新过程分为两个阶段，第一阶段是通过交叉操作实现EXS解集的全局更新;第二阶段是根据每个子种群中最优个体占EXS解集的比例，也即是每个子种群对EXS解集的贡献量来选择交叉算子进行局部搜索，当贡献量大的子种群所选的交叉算子为SBX时，EXS解集中的个体两两交叉更新，当贡献量大的子种群所选的交叉算子为SBX時，EXS解集中的个体3个个体之间交叉更新，由此完成一次迭代过程，当迭代次数到达上限时所产生的Pareto前沿解即为最优的多目标优化解，此种更新过程可以使最优解集在全局和局部2个层次进行覆盖性搜索，使其收敛性能大大增强。

3.3 子种群的自适应调整

由于不同的交叉算子迭代产生的个体分布数量不同，因此，随着种群迭代过程的推进，需要动态调整各个子种群的数量，种群的调整规则为个体总数NP不变，自适应调整子种群大小，增加Pareto前沿分布密集合理的子种群数量，减少分布不合理的子种群数量，具体的子种群数量调整规则：

随着迭代次数的增加，种群中优势个体的数量会激增，为了防止早熟现象发生，当某一子种群Subi的个体数目小于其最小限制nmin时，需要调整优势种群的数目，即从优势种群中剔除掉nmin-Subi个体以保证最小子种群数量和维持种群总数NP不变。

3.4 可用输电容量优化决策的求解流程

根据以上对NSGA-Ⅱ算法的改进，将其应用至多区域可用输电容量协调决策的求解中，具体计算流程如下：

1）输入原始数据，并设置算法的最大迭代次数tmax、种群规模NP、变异步长F、交叉算子SBX、SPX的参数;

2）随机生成初始种群，并利用图2所示的外部最优解的初始化过程，对多区域可用输电容量决策模型的目标函数进行种群初始化操作;

3）对于各个子种群中的每个个体，改变电源和负荷的样本数据，并根据2.2节三点估计法得到各子区域的ATC概率密度分布fpd，计算各子区域目标函数Wm，检验每个个体是否满足约束以及不满足的程度;

4）参照文[19]对各子种群进行遗传操作，得到第t代子种群;

5）根据第t代子种群中个体负荷水平、风电出力，对机组出力和负荷水平进行调整，然后按照第3）步计算目标函数值并效验约束条件;

6）对各子种群中生成的子代个体与父代一同进行非劣排序和拥挤距离排序;

7）为了防止早熟，调整子种群规模保证子种群个体的最低数量，挑选出NP个个体作为t+1代父种群，并更新外部最优解;

8）若t≥tmax，迭代结束，否则，转入步骤4）;

9）输出分布合理、Pareto前沿密集的最优解。

4 算例验证

假设该地区盈余电力允许外送的前提下，研究该地区通过500kV联络线对省内和省外区域输送电力情况，拓扑接线如下图4所示。主要经济参数的取值为：该地区至省内区域的单位时间、单位容量的ATC价值为560元/MW·h，输电中断时所需支付的单位ATC赔偿系数为1120元/MW·h，该地区至省外区域的单位ATC价值为500元/MW·h，输电中断时所需支付的单位ATC赔偿系数为1000元/MW·h。假设该地区用S简称，省内区域用Q简称，省外区域用K简称。

4.1 收敛性能指标和参数设置

多目标优化算法目的是所求得的最优解逼近真实最优解，该算法的收敛性能基本是通过求最优解和真实解之间的距离进行评价，因此，本文采用GD指标来评价算法收敛性能。

1）评价指标。

式中di为求得的外部最优解至真实最优解之间的欧氏距离。

为了对比改进后的NSGA-Ⅱ算法的性能，采用文[15]中基于传统NSGA-Ⅱ的方法同步计算本文所求解的多区域ATC协调决策模型。

2）参数设置。

种群中个体的数量NP=100，外部最优解个数NEXS=100，传统NSGA-Ⅱ和改进后的NSGA-Ⅱ各迭代求解5000次，交叉算子SBX和SPX的参数设置为：η=20、ε=1，变异步长F=20。

4.2 子区域ATC概率分布

为了验证三点估计法求取可用输电容量时更加精准高效，采用文[15]的蒙特卡洛仿真技术求取区域S至Q的ATC概率密度分布作为基准数据，其中蒙特卡洛仿真次数5 000次，采用文[9]基于稀疏多项式展开的概率ATC计算方法作为对比方法，以上3种方法得到的可用输电容量的均值、相对误差和耗时如表1所示。

从表1中3种方法求取的结果可以看出，三点估计法的计算效率远高于蒙特卡罗仿真法和稀疏多项式混沌展开法，并且相对误差很小可忽略不计，因此采用三点估计法所得的结果更加高效精准。

图5和图6分别展示了由三点估计法求取的区域S至Q和区域S至K的ATC概率密度分布。

根据三点估计法得到的该地区至省内和该地区至省外的ATC的概率密度分布后，采用改进的NSGA-Ⅱ算法对多区域ATC协调决策模型进行求解。

4.3 算法仿真结果

为了对比改进后的NSGA-Ⅱ算法的收敛性能，将两种算法分别在ZDT-2[20]测试问题中计算100次，统计GD指标的中位数Xm和四分位数IRQ评价结果如下表2所示。

通过比较表2的结果可知，采用改进后的NSGA-Ⅱ算法所得最优解的中位数和四分位的GD距离均优于传统的NSGA-Ⅱ，表明本文所采用改进后的NSGA-Ⅱ方法求解多区域可用输电容量决策模型时具有较好的收敛性能。

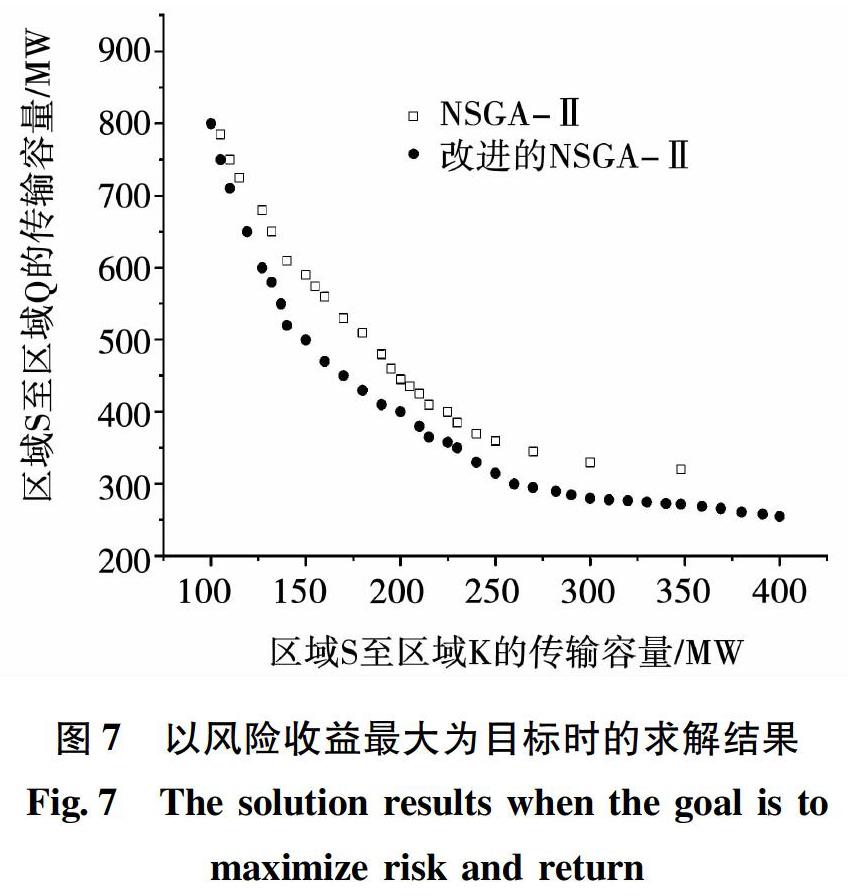
采用两种优化方法分别迭代5000次后，得到本区域至省内及省外的可用输电容量协调优化结果如图7所示。

从图7两种算法的优化结果可以表明，改进的NSGA-Ⅱ的Pareto前沿解均匀、密集，且最优解集范围更大，有利于决策者按照不同的要求选择合适的输电容量。

采用分布合理密集的Pareto前沿解得到极端情况下不考虑多区域协调限制的两种方案以及折中最优方案，3种方案的收益如下表3所示。

对Pareto解集的几种组合方式进行风险收益计算，得到最大风险收益为497310元的ATC决策组合为：该区域至省内的最优传输容量是800MW、该区域至省外的最优传输容量是104.6MW。

5 結 论

针对目前NSGA-Ⅱ算法存在的种群单一导致的早熟和收敛性能差的问题，本文对其进行改进并应用到多区域可用输电容量的协调优化决策，得到如下结果：

1）相比蒙特卡罗仿真技术和稀疏多项式混沌展开法，采用三点估计法得到多区域ATC的概率密度分布高效精准。

2）通过仿真结果的GD距离指标表明所构建的多种群、多交叉算子、自适应调整优势种群的改进NSGA-Ⅱ算法，其收敛性优于传统NSGA-Ⅱ。

3）与NSGA-Ⅱ相比，改进后的NSGA-Ⅱ算法所求得的多区域可用输电容量协调优化结果的Pareto前沿分布均匀、密集和更接近最优解。

参 考 文 献：

[1] 鲍颜红，张金龙，江叶峰，等.考虑新能源出力不确定性的可用输电能力在线评估方法[J].电力自动化设备，2020，40（4）：71.

BAO Yanhong， ZHANG Jinlong， JIANG Yefeng， et al. Online Evaluation Method of Available Transmission Capacity Considering Uncertainty of New Energy Output [J]. Electric Power Automation Equipment， 2020，40（4）：71.

[2] 李锴，党杰，孙鑫，等.计及风电功率不确定性的电力系统输电可靠性裕度快速评估[J].电网技术，2019，43（9）：3337.

LI Kai， DANG Jie， SUN Xin， et al. Rapid Assessment of Power System Transmission Reliability Margin Considering Wind Power Uncertainty [J]. Power System Technology， 2019，43（9）：3337.

[3] DU P， LI W， KE X， et al. Probabilistic-Based Available Transfer Capability Assessment Considering Existing and Future Wind Generation Resources[J]. IEEE Transactions on Sustainable Energy， 2015， 6（4）：1.

[4] 王成山，王兴刚，孙玮.含大型风电场的电力系统概率最大输电能力快速计算[J].中国电机工程学报，2008（10）：56.

WANG Chengshan， WANG Xinggang， SUN Wei. Fast Calculation of Probability Maximum Transmission Capacity of Power System with Large Wind Farms [J]. Proceedings of THE CSEE， 2008（10）：56.

[5] 罗钢，石东源，蔡德福，等.计及相关性的含风电场电力系统概率可用输电能力快速计算[J].中国电机工程学报，2014，34（7）：1024.

LUO Gang， SHI Dongyuan， CAI Defu， et al. Fast Calculation of Probability Available Transmission Capacity of Power System Including Wind Farm Considering Correlation [J]. Proceedings of THE CSEE， 2014，34（7）：1024.

[6] 闫炯程，李常刚，刘玉田.基于SDAE特征提取的含风电电网可用输电能力计算[J].电力系统自动化，2019，43（1）：32.

YAN Jiongcheng， LI Changgang， LIU Yutian. Calculation of Available Transmission Capacity of Power Grid with Wind Power based on SDAE Feature Extraction [J]. Automation of Electric Power Systems， 2019，43（1）：32.

[7] RODRIGUES A B， SILVA M G D. Chronological Simulation for Transmission Reliability Margin Evaluation with Time Varying Loads[J]. International Journal of Electrical Power & Energy Systems， 2011， 33（4）：1054.

[8] 陈金富，孙鑫，段献忠，等.基于机会约束规划的含风电场电力系统可用输电能力计算[J].中国电机工程学报，2019，39（23）：6804.

CHEN Jinfu， SUN Xin， DUAN Xianzhong， et al. Calculation of Available Transmission Capacity of Power System with Wind Farms based on Chance Constrained Planning [J]. Proceedings of THE CSEE， 2019，39（23）：6804.

[9] 孙鑫，王博，陈金富，等.基于稀疏多项式混沌展开的可用输电能力不确定性量化分析[J].中国电机工程学报，2019，39（10）：2904.

SUN Xin， WANG Bo， CHEN Jinfu， et al. Quantitative Analysis of Available Transmission Capacity Uncertainty based on Sparse Polynomial Chaos Expansion [J]. Proceedings of THE CSEE， 2019，39（10）：2904.

[10]OTHMAN M M ， RAHMAN N A ， SASI D S ， et al. Inter-area Transfer Capability Assessment Considering Optimal Flexible Solutions of Capacity Benefit Margin[C]// IEEE International Power Engineering & Optimization Conference Melaka. IEEE， 2012.

[11]KHATIR A A ， ETARD V ， CHERKAOUI R. Assessment of Total Transfer Capability for Simultaneous Transactions in Decentralized Multi-areas Power Systems[C]// IEEE Power & Energy Society General Meeting. IEEE， 2012.

[12]李岩，张光武.混合NSGA-Ⅱ和DE的优化算法及应用[J].哈尔滨理工大学学报，2018，23（5）：75.

LI Yan， ZHANG Guangwu. Optimization Algorithm and Application of Mixed NSGA-Ⅱ and DE [J]. Journal of Harbin University of Science and Technology， 2018，23（5）：75.

[13]毕晓君， 王朝. 一种基于参照点约束支配的NSGA-III 算法 [J]. 控制与决策， 2019， 34（2）：1.

BI Xiaojun， WANG Chao. A Reference Point Constrained Dominance-based NSGA-III Algorithm [J]. Control and Decision， 2019， 34（2）：1.

[14]CHEN F ， ZHOU J ， WANG C ， et al. A Modified Gravitational Search Algorithm based on A Non-dominated Sorting Genetic Approach for Hydro-thermal-wind Economic Emission Dispatching[J]. Energy， 2017， 121：276.

[15]黄裕春，杨燕，文福拴，等.计及风险控制的多区域ATC概率优化协调决策模型与方法[J].电力自动化设备，2013，33（3）：84.

HUANG Yuchun， YANG Yan， WEN Fushuan， et al. Model and Method of Probability Optimization Coordination Decision for Multi Regional ATC Considering Risk Control [J]. Electric Power Automation Equipment， 2013，33（3）：84.

[16]潘炜，刘文颖，杨以涵.概率最优潮流的点估计算法[J].中国电机工程学报，2008（16）：28.

PAN Wei， LIU Wenying， YANG Yihan. Point Estimation Algorithm of Probabilistic Optimal Power Flow [J]. Proceedings of THE CSEE， 2008（16）：28.

[17]DEB K， PRATAP A， AGARWAL S， et al. A Fast and Elitist Multiobjective Genetic Algorithm：NSGA-II[J]. IEEE Transactions on Evolutionary Computation， 2002， 6（2）：182.

[18]TSUTSUI S. Multi-parent Recombination with Simplex Crossover in Real Coded Genetic Algorithms[J]. Gecco，1999：657.

[19]S. DAS， P. N. Suganthan. Differential Evolution：A Survey of the State-of-the-Art[M]. IEEE Press， 2011.

[20]ZITZLER E，  DEB K， THIELE L. Comparison of Multiobjective Evolutionary Algorithms：Empirical Results[J]. Evolutionary Computation， 2000， 8（2）：173.

（編辑：温泽宇）