基于SOLO分类的数学试卷设计与开发
□高 琼 高建成
(1.浙江师范大学附属杭州笕桥实验中学,浙江杭州 310008;2.杭州市余杭区教育发展研究学院,浙江杭州 311120)
一、问题提出
目前,初中数学试卷的命制,基本是按照心理学家布卢姆的教育目标分类进行的.布卢姆教育目标分类用于测验的设计,关注的是教学目标,致力于知识与技能描述,以此来区分习得结果,但不同类别的学生对同一问题的理解和回答,反映了认知结构的差异,体现出思维水平上的质的差别.这些差异和差别用布卢姆分类来分析是无法做到的,因为它关注的是知识呈现,关注的是表象,而不是评价学生掌握知识背后的思维品质和认知层次,更不是评价学科内在的本质.
教育心理学家彼格斯和卡利斯的SOLO分类评价理论,关注学科内在本质,着重于对学生学习品质及学科核心素养进行评价.知识点的多与少、技能的生与熟只涉及评价中量的层面,而学生学习的状态、思维的获得、认知的丰富、能力的提升、素养的提高等这些评价中质的层面,正是SOLO分类评价的重点.因此,SOLO分类评价从学生的知识、技能到思维、认知、素养层层深入,全面而深刻,基于该理论命制的数学试卷能够有效控制试卷的难度,保证试卷的信度和效度.
二、理性分析
SOLO分类理论是基于皮亚杰的认知发展理论而延伸细化出来的分类理论,它从观察到学习结果的结构出发,定量地用五个层次来描述学生思维和认知发展过程,全面分析学生知识与技能内化的品质,考查学生核心素养的获得过程,并用结构呈现来解释学生的反应,确定不同的反应所对应的五种结构或五个层次水平.
从前结构反应到拓展抽象结构反应,SOLO分类法提供了一种由量变到质变的结构测量方法,它不是对与错的二元论式的简单评价,而是对不同的学生指向不同水平的再认知,并据此进行个性化教育.因此,SOLO分类不仅可以帮助教师“因材施教”地制定多级教学目标,还可以“把脉”学生学习中的困难,精准定位学生思维水平和认知层次,从而用于测验和考试的内容结构框架.
例如,我们可以通过对“怎样的两个数,它们的和等于它们的积?”的回答来分析学生的思维、认知水平.
前结构反应:信口说出了一个完全无关、不合逻辑的简单的判断,如(1,0).
单一结构反应:从学生看到题目一开始,慢慢吞吞,当好不容易得出了一个答案,如(2,2),即兴高采烈,停止作答.
多元结构反应:学生两眼有光,但慢慢吞吞,得出一个答案后,再拼凑出第二个,以至多个,但不能发现这些答案背后之间的联系,如
关联结构反应:学生动作迅速,思维敏捷,不但能想出多个答案,并能及时发现它们之间的联系,如通过对几组数的观察发现:这两个数的分母之和等于分子,且分子相同.

从上述的分析中可以看出,SOLO分类理论是一个由简单到复杂、由量变到质变的层次结构体系,是从“张嘴吃到桃”,到“伸手摘到桃”,再到“跳跳得到桃”,最后到“制造工具获得桃”的一个系统的认知与思维的发展过程.前三个层次是基础知识和基本技能的积累,在试卷上体现的是基础题;后两个层次是理性思维的飞跃,在试卷上关联结构反应是中等偏难题,拓展抽象结构反应是难度题.而要实现思维能力的突破、核心素养的发展,又离不开基础知识的夯实、基本技能的积累.因此,我们必须对《义务教育数学课程标准(2011年版)》进行认真的分析与解读,仔细研究标准中涉及的知识、技能、活动经验及数学基本思想,分析其包含的思维特征、思维品质、认知水平和数学核心素养.这样,数学考试才有针对性,才能有效控制试卷的难度,保持较高的区分度.
三、设计与开发
根据文献资料的查阅,我们发现,基于SOLO分类理论进行试卷的开发,一般要经历以下几个步骤:①研究课标;②结合SOLO分类制定双向细目表;③命制试题;④先期诊断;⑤预测“三度”(信度、难度、效度);⑥修改并完成测试卷.
在试卷开发的这六个步骤中,制定双向细目表尤其重要,双向细目表是试卷命制的“准绳”,它是一种考查内容和考查能力(目标)之间的关联表.考试命题双向细目表本质上就是课程内容和学习结果两个维度,其中一维反映课程的内容,另一维反映学生的学习品质.SOLO分类指导下的双向细目表在课程内容上并无变化,只是在学习品质上用SOLO的后四个层次水平来进行分类.
由于按SOLO分类,学生对问题的反应特征是有层次的,并按“前结构—单一结构—多元结构—关联结构—拓展抽象结构”顺序递进.显然,如果学生利用了一个知识点,使用了一种技能,解决了一个数学问题时,那么知识、技能与数学问题之间建立单一联系,也就实现了单一结构反应,如果不能实现单一结构反应,那就更不可能实现多元结构反应及关联结构反应,更不可能实现拓展抽象结构反应,这样的话,只能认定为前结构反应,因此,前结构反应在测试双向细目表中就不单独列出.
根据SOLO分类评价理论分析,要使整张试卷难度系数保持在0.75左右,必须在双向细目表中保持单一结构、多元结构、关联结构、拓展抽象结构的试题分值比在3∶4∶2∶1左右,这样才能保证数学试卷内既有一定的知识技能目标考查,又有对学生思维认知发展和升华的考查(如表1).
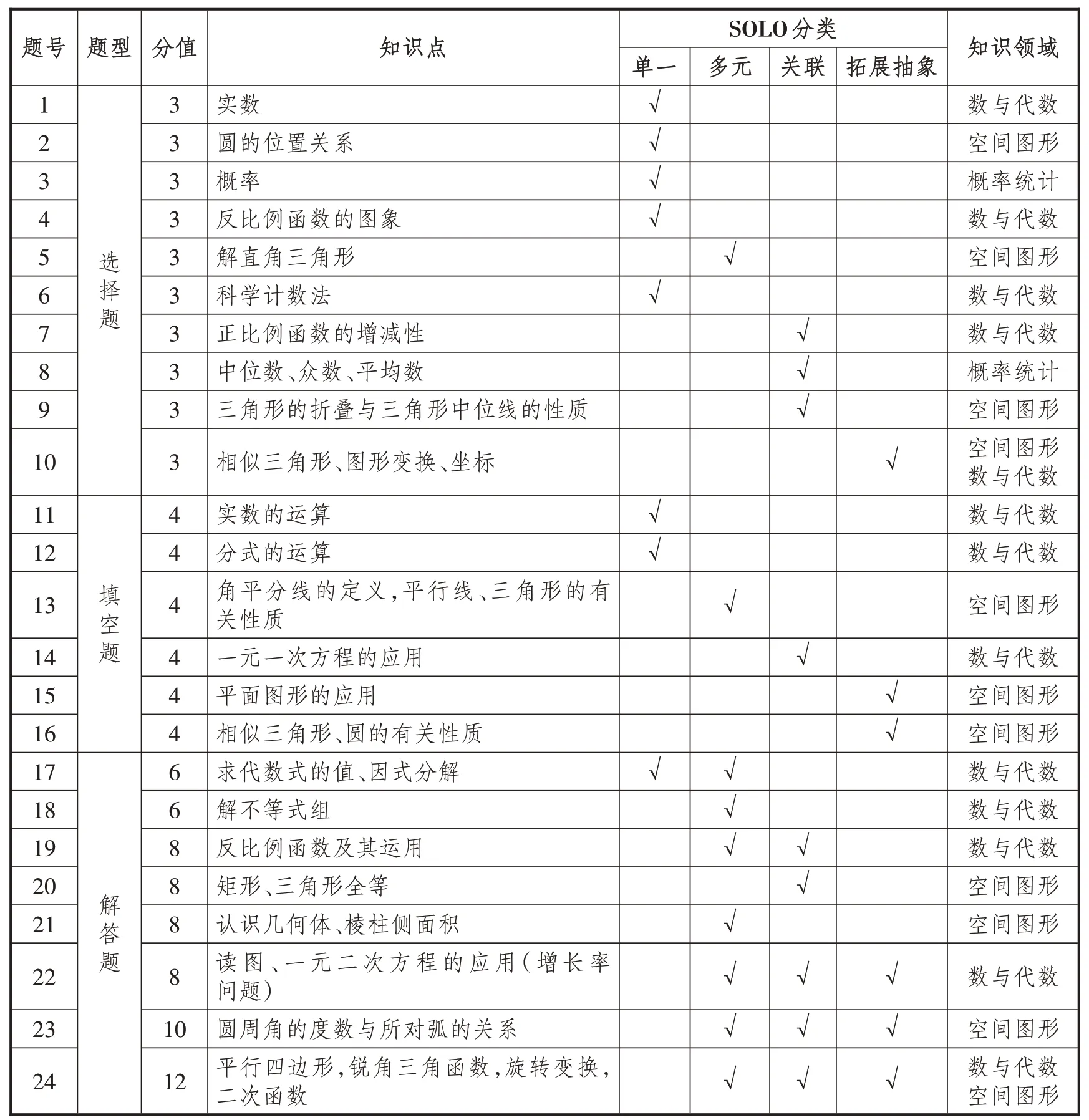
表1 SOLO分类设计初三数学测试双向细目表
紧接着,按照双向细目表进行试卷的命制.双向细目表是试卷命制的准绳,命题人应严格按照双向细目表里所列的检测内容、题型、所占的分值及SOLO分类层次进行命题.按照这一“模板”进行命题,极为简便,就像中医院的药剂师按老中医所开处方进行分拣、称量、配药一样,快捷而准确.
同时,在命制解答题时,要尽可能编成符合四个层次的四个小问题,这四个小问题涉及的知识点由少到多,难度由易到难,情境由简单到复杂,但不管怎样设计,都要求每一个小问题体现一个SOLO层次,这样,四个小问题就构成一道蕴含知识、技能、思想和素养的SOLO试题.例如某初中毕业生学业模拟考试卷第22题.
22.(本题12分)2021年3月20日至25日,新冠病毒在某地快速传染,每天的统计病例人数如图1所示.

图1
(1)在3月20日至3月25日这6天中,某地累计确诊的“新冠”病例人数最多的是哪一天?有多少人?(单一结构)
(2)在3月21日至3月25日这5天中,某地平均每天新增加“新冠”确诊病例多少人?(多元结构)如果接下来的几天中,继续按这个速度增加,那么到3月29日这一天,估计该地“新冠病毒”新增病例将达到多少人?(关联结构)
(3)新型冠状病毒的传染性极强,某地因1人感染了新型冠状病毒而没有及时隔离治疗,经过两天传染了9人,平均每天一个人传染了几个人?如果按照这个传染速度,再经过5天后,这个地区一共将会有多少人感染新型冠状病毒?(拓展抽象结构)
上述具有现实意义的四个小问题,从思维的结构层次我们可以清晰地发现,四个现实小问题是按照从易到难、从简单到复杂、由现象到本质的顺序排列的,前面的小问题处在思维的底层,后面的小问题处在思维的高层,后面的小问题是前面小问题的拓展和延伸,层级明显.因此,教师在评分时,可根据学生回答了本题中的第一个小问题,判断学生只掌握了一个相关的知识点,具备了一种技能,达到了单一结构的反应,评分者据此给2分;如果学生能够正确回答本题中前两个现实小问题,可判断学生掌握了多个相关的知识点,具备了多种技能,达到多元结构的反应,可以据此给5分;如果学生能够正确回答本题中前三个现实小问题,可判断学生不但掌握了多个相关的知识点,具备了多种技能,而且还能将前后知识进行整合并系统化,产生新的判断,则表明达到关联结构的反应,可以据此给8分;如果学生能够正确回答所有四个现实小问题,可判断学生掌握了相关知识,具有了相关能力,具备了一定的数学思想,能创造性地解决问题,产生新的判断和预测,则表明达到了拓展抽象结构反应水平,据此可给12分.这样按结果进行排序、赋分,既不会多给分,也不会少给分,能保证分值与学生数学学习能力的匹配,能有效地保证数学试卷的信度、难度、区分度.
四、误差分析
2021年5月16日,我们依据SOLO评价理论改编了某年的衢州中考数学测试卷而成为一套中考模拟卷,并在全校九年级学生检测中运用,同时我们还要求相关教师依据此理论对主观题进行评卷.
通过相关数据的收集分析,结果是令人欣慰的.首先,整套试卷的难度系数是0.742,学生考完后都很自信.其次,统计初三群体试卷,发现主观题与客观题的相关系数为0.85,属于强相关.也就是说,主观题回答得简洁、清晰、准确,得分高,客观题的得分就高;反之,主观题回答烦琐、混乱、模糊,得分低,客观题的得分也低.这在一定程度上说明本次模拟试卷的信度较高.再次,运用SOLO分类理论制定的评分细则,其误差率小.通过抽样分析我们发现,不同的人评卷,1分的误差在8%左右;2分的误差仅有1%,不存在3分以上的误差;这与之前动辄5分以上的误差,已经进步了很多,让阅卷老师得心应手.因此,基于SOLO评价理论进行的命题设计、评分方法,能够反映数学核心素养的要求,保证信度、难度、效度,它让数学考试从过去的“背诵性”“模式性”转向“方法性”“应用性”“思想性”“人文性”.

