基于GaN FET的1 MHz多路CLLC双向直流变换器

侯宇琦，王萍，王议锋，陈博

（天津大学智能电网教育部重点实验室，天津 300072）

目前，能源和环境问题的日益严重，可再生能源和分布式储能系统的发展受到广泛关注[1-2]。随着电力电子技术的飞速发展，分布式储能系统迫切需要高效率、高功率密度的充放电控制器。使得变换器具有转换效率高、体积小、重量轻、节省空间且使用灵活等优点，以适用于各种应用需要，实现更高的经济价值[3-4]。

为了实现高功率密度，必须提高变换器的开关频率来降低无源元件的体积。然而，较高的工作频率同时也造成了开关损耗、磁性元件损耗的增加，最终导致变换器工作效率降低。更严重的是，寄生参数的影响在高频条件下将变得尤为显著。这些都会制约变换器的性能。如何实现变换器的高频、高效率及高功率密度，已成为学者们研究的热点。目前，研究者们主要从三个方面来解决这一问题：新型宽禁带器件的应用、磁集成技术的研究以及谐振拓扑的改进。

近年来，随着半导体功率器件的快速发展，传统硅器件的潜力已经得到了充分开发。碳化硅（SiC）和氮化镓（GaN）等新型宽禁带器件凭借着优良的材料特性，已逐步取代传统硅器件被应用于一些特定场合。特别是在高频条件下，GaN器件凭借其低导通阻抗和极短的响应时间而备受关注[5-10]。一些学者关注于GaN的特性以及驱动器设计。文献[6-8]基于MHz等级频率场景，建立了GaN FET的结构以及损耗模型。同时，部分学者针对GaN器件的实际应用进行探索。文献[9]将GaN器件应用于1～5 MHz反激变换器，获得了理想的工作特性，最高效率可达98%。文献[10]结合GaN器件提出了Non-inverting Buck-Boost变换器，在10 MHz工作频率情况下，获得了94.4%的工作效率和6.25 W/cm3的功率密度。GaN在高频条件下具有广阔的应用前景。然而，由于其器件固有特性，会导致较大的开通损耗。因此，应用GaN器件，迫切需要零电压开关（zero voltage switching，ZVS）特性的实现。同时，在高频情况下，磁性元件的损耗会相应增加，漏感等寄生参数也会对变换器的性能产生不良影响。为了解决这些问题，平面磁性元件和磁集成技术在高频环境中得到了广泛应用[6，9，11-12]。学者通常采用优化磁性元件布局和绕组布线方式来改善磁性元件性能，并使损耗最小化。此外，通过这些方法，可以显著抑制寄生参数对变换器造成的不利影响。

在此基础之上，拓扑结构的选择对变换器的设计至关重要。谐振拓扑可以实现较好的软开关特性，使功率器件开关损耗显著降低，改善变换器效率[6，13-22]。因此，串联谐振（series resonant circuit，SRC）、并 联谐振（parallel resonant circuit，PRC）、LLC谐振和其他一些谐振拓扑被广泛应用于各种场合[13-17]。其中LLC谐振拓扑在高频下仍表现出优异性能，引起了众多学者的关注。文献[16]研制了一台高功率密度、高工作效率的1 MHz LLC谐振变换器，并验证了高频条件下变换器仍然可以实现ZVS和ZCS。然而，LLC谐振拓扑在双向功率变换的应用场景下存在一些局限性[18]。一方面，它的反向电压增益有限，不适用于能量存储系统。另一方面，高增益特性与高效率之间存在着难以调和的矛盾。针对这些问题，在LLC谐振拓扑基础上，文献[18-20]提出了许多改进型拓扑，诸如CLLC，CLTC和CLLLC结构，均得到了良好的效果。但是目前大多在低频下开展研究，对于高频下双向谐振变换器的研究仍需进一步展开。

本文采用GaN器件和磁集成技术，设计出适用于1 MHz工作场景下，具有高效率、宽电压调节范围的双向谐振变换器。为了同时实现高增益特性和高效率的双向功率转换，本文利用CLLC拓扑具有全负载范围内软开关特性以及低关断损耗的同时，可以实现功率的双向流动且正反向工作过程对称的良好变换特性，以此作为理论基础进行拓扑改进。变压器组采用高压侧串联、低压侧并联的连接方式，在变换器低压侧三路并联，以减少通过开关管的电流，降低导通损耗达到提高变换器效率的目的。同时，为了进一步提升功率密度，拓扑采用非对称半桥结构以缩小变换器体积。在磁性元件设计上，通过采用磁集成和平面磁件的方法，以PCB绕组代替传统的线圈，抑制寄生参数对变换器造成的不利影响，提高变换器的功率密度。同时，借此也可以保持变压器较高的一致性，便于制作。

本文的主要内容如下：第1节详细介绍了变换器的拓扑结构和工作原理；第2节对变换器的工作特性和参数设计方法进行了分析研究；第3节阐述了平面磁集成方法和布线改进策略；第4节对变换器进行了实验验证，给出实验结果。

1 拓扑结构与工作原理

1.1 拓扑结构

该拓扑结构由三部分组成，包括高压侧（high voltage side，HVS）半桥、低压侧（low voltage side，LVS）半桥和CLLC谐振腔，如图1中3个虚线框（从左至右顺序）所示。此外，采用多支路并联的方法来减小低压侧开关管的电流应力并提高工作效率。这里，选取支路数x的值为3。

图1 Multi-CLLC的拓扑结构Fig.1 The structure of multi-CLLC

1.2 模态分析

当变换器工作在降压模式时，与传统单路CLLC拓扑相类似，根据开关频率fs与主谐振频率fr_m的关系，变换器可以工作在连续模式（continue conduction mode，CCM）和断续模式（discontinuous conduction mode，DCM）。主要波形如图2所示。从图2波形上来看，在半个周期内DCM有四个不同的工作模态，而CCM则为三个。

图2 Multi-CLLC的降压模式下工作波形Fig.2 Waveforms of multi-CLLC in step-down mode

t0—t1：t0时刻，关断开关管 S2，此时，所有开关管都处在关断状态，即进入死区时间，等效电路如图3a所示。谐振电感电流ir开始给开关管的寄生电容Cs2充电，给Cs1放电。合理设计死区时间，使寄生电容充放电的时间小于死区时间，来保证实现开关管的软开关；

t1—t2：t1时刻，开关管输出电容充放电完成，谐振电感电流ir通过开关管的寄生二极管DS1续流，直到t2时刻S1开通，此时开通电压为零，实现零电压开关（ZVS），等效电路如图3b所示；

t2—t3：t2时刻，开关管S1导通，等效电路如图3c所示，功率通过谐振腔从高压侧传输到低压侧。此时谐振腔由 Lr，Cr，Lmx和 Crx构成。谐振电流ir呈现正弦波；

t3—t4：等效电路如图3d所示，当ir等于励磁电流ilm1时，ir被励磁电流ilm1钳位，低压侧没有电流流过，Lr，Cr和Lmx构成新的谐振腔。因此 S1持续导通，但没有功率传输到低压侧。值得注意的是，最后阶段仅存在于DCM模式中。

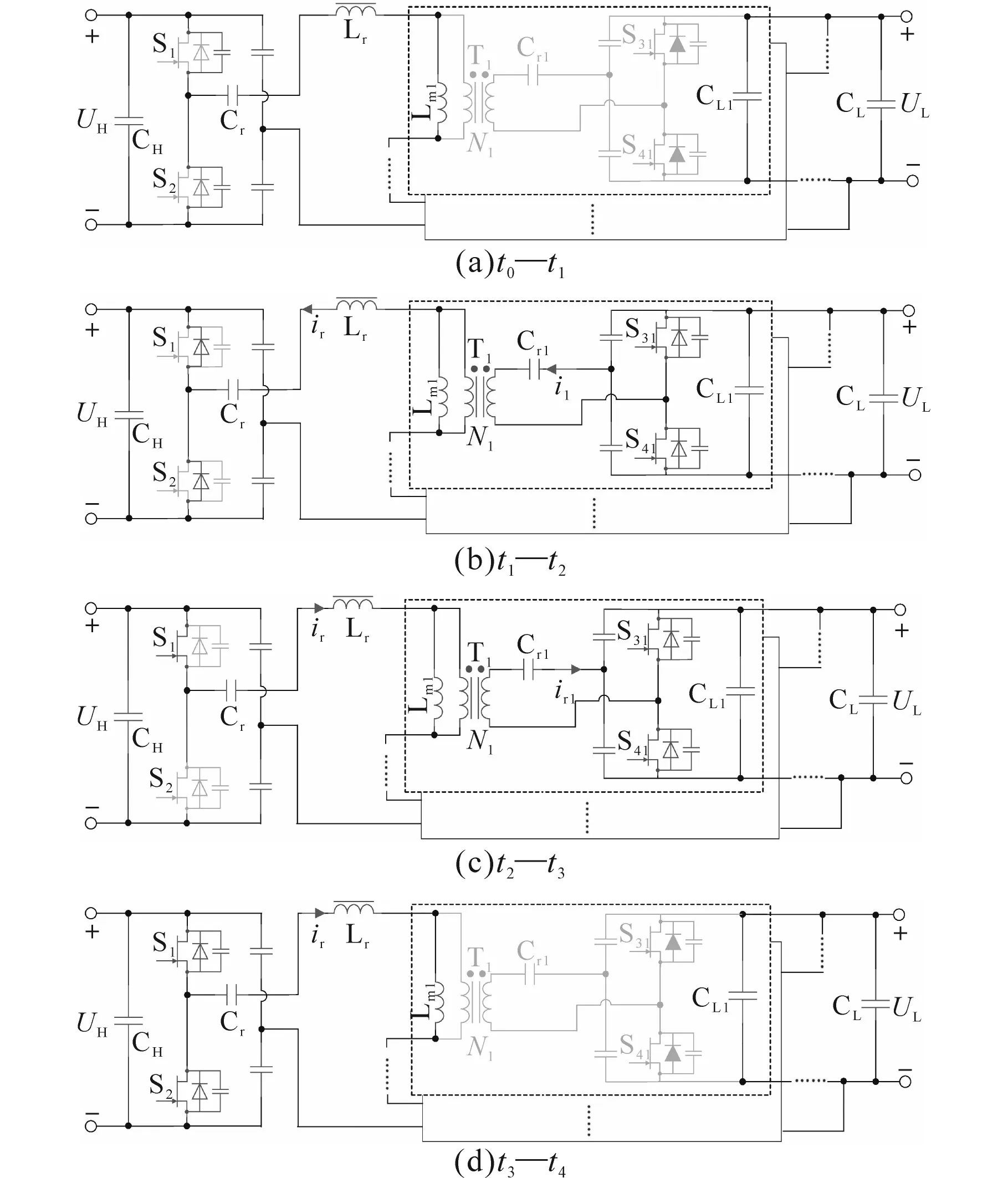
图3 Multi-CLLC的降压模式等效电路模型Fig.3 The equivalent mode of multi-CLLC in step-down mode

对于升压模式，其工作过程与降压模式类似。在此不再赘述。

2 拓扑建模与参数设计

目前，文献[19，21-23]已经提出了一些关于CLLC拓扑稳态特性的参数设计和优化的方法。但是，上述分析方法多针对单路输出的拓扑结构。因此，这里需要专门建立Multi-CLLC的通用数学模型。

与传统的CLLC拓扑结构类似，为了简化计算过程，我们采用基波近似（fundamental harmonic approximation，FHA）法进行分析，并给出了相应的等效模型，如图4所示[24]。

图4 Multi-CLLC的FHA等效模型Fig.4 The FHA equivalent mode of multi-CLLC

2.1 谐振频率分析

根据第一节的分析，在降压模式中有两个不同的谐振腔情况。当有功率传输时，谐振腔由Lr，Cr和Cx（x指1～n）组成，如图4所示。基于基尔霍夫定律，此时的输入和输出电压可以表示为

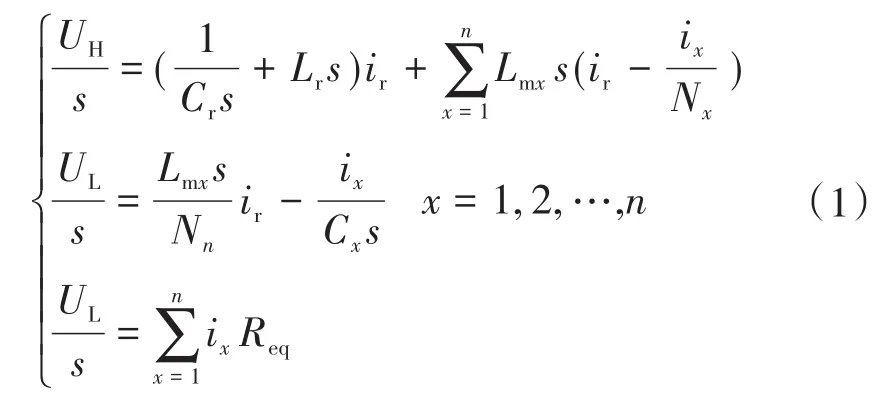
其中

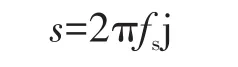
式中：UH，UL分别为高压侧和低压侧的电压；ix为低压侧支路中电流；Cx，Lmx和Nx分别为x支路的谐振电容、励磁电感和变压器匝数比；Lr，Cr分别为高压侧的谐振电感和电容；Req为输出交流等效电阻；fs为开关频率。

所有支路都采用相同的元件参数可以简化变换器设计，并避免不同支路之间的环流。此外，虽然随着支路数的增加，低压侧开关管的电流应力得到缓解，效率得到提高，但同时开关管的数量和成本也相应提高。因此，为了兼顾成本、效率和电流应力，低压侧最终采用三路并联的结构。

由式（1）可得：

假设等效电阻Req为0，当开关频率fs等于主谐振频率fr_m时，输入阻抗应该为0。基于该理论和式（2），得到fr_m：

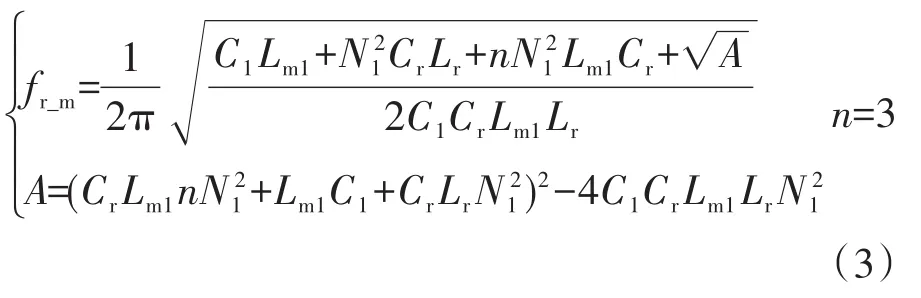
当变换器没有功率传输到低压侧时，谐振腔由Lr，Cr和Lmx构成。此时的谐振频率作为第二谐振频率f2_d，表示为

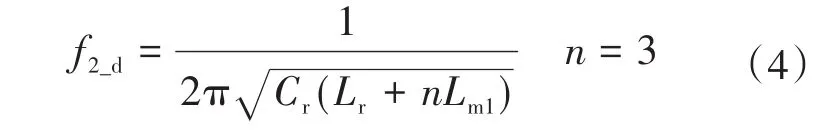
对于升压模式采用同样的分析方法，其主谐振频率与式（3）相同。它的第二谐振频率f2_u为

2.2 电压增益特性

根据应用条件，需要考虑变换器的电压等级和输出电压范围。分析电压增益特性对参数设计具有重要的作用。

在输入和输出电压表达式的基础上，降压模式的电压增益Md表示为

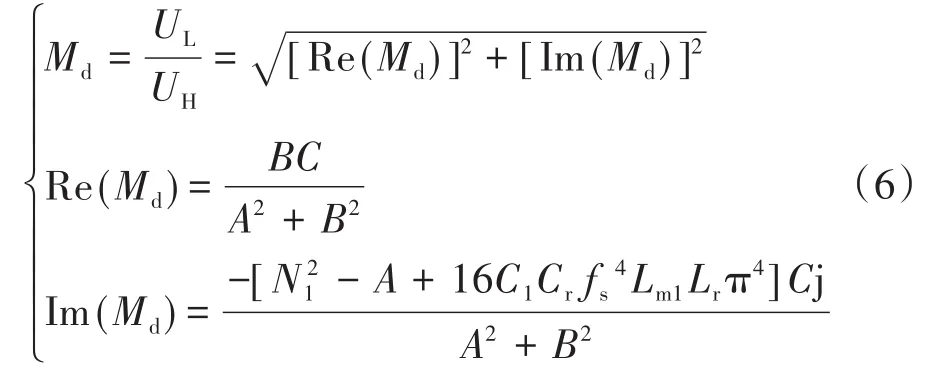
其中

式中：Re（Md），Im（Md）分别代表Md的实部和虚部；A，B，C为中间变量；Req为高压侧的交流等效电阻。通过此分析方法，可以得到升压模式下的电压增益。

随着电流方向的改变，输入和输出电压可改写为下式：升压模式的电压增益Mu为

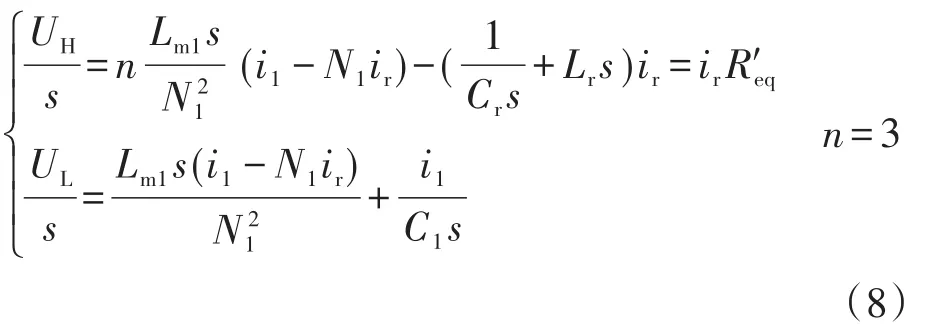
其中，中间变量A′，B′和C′表示为

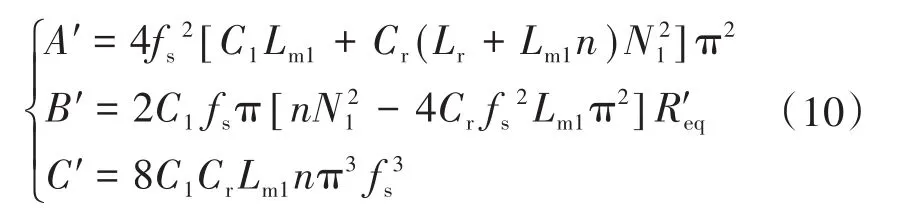
结合式（6），式（7），式（9）和式（10），可得到Multi-CLLC不同负载下双向运行的电压增益曲线，如图5所示。

图5 Multi-CLLC不同负载下双向运行增益曲线Fig.5 The bidirectional operating voltage gain curves of the multi-CLLC under different loads

将电压增益和频率归一化，虚线的区域表示变换器的工作区间。如图5所示，由于采用FHA法忽略了高次谐波的影响，计算精度随着fs偏离fr_m而降低。但在工作区间内，其精度满足设计要求。结果表明，变换器具有在较窄频率范围内实现宽范围电压调节的能力。

2.3 阻抗角

阻抗角是保证ZVS实现的关键因素。特别是在高频情况下，开关损耗将导致工作效率急剧下降。

另外，对于GaN FET而言，与关断损耗相比，开通损耗对效率的影响更为严重，没有实现零电压开通会导致极大的开通损耗。ZVS的实现是保证变换器高效率的关键。对于谐振型变换器，工作在感性区间有利于实现ZVS。

通过阻抗角的计算可以确保变换器工作在感性区间。但是，过大的阻抗角将会导致两个问题：1）关断电流增大，导致开关管在峰值电流关断；2）开通电流增大，同步整流驱动延时将导致额外的损耗。

通过对应的输入电压和输入电流可以得到两种模式下的阻抗角（φd，φu），表示为

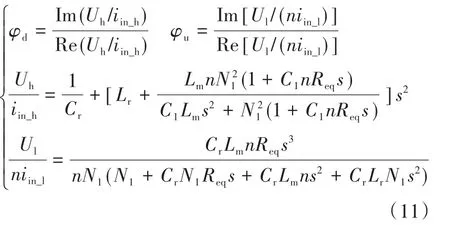
GaN FET具有较差的第三象限工作特性，同步整流开关管应用时，驱动延时将导致变换器效率急剧下降，甚至特性发生改变。因此，阻抗角φd，φu应该大于0，以保证变换器在感性区间内工作，同时还要接近于0，才能保证变换器效率。

2.4 参数设计

本文所提拓扑主要应用于分布式储能充放电控制，因此，高压侧（母线侧）额定电压为400 V，低压侧（电池侧）输出电压设定为18～24 V，主谐振频率设定在1 MHz左右，对应开关频率调节范围0.6 ～1.2 MHz。

根据上述分析和计算公式，变换器参数设计依据和约束条件如下：1）GaN开关特性和低压侧电流确定并联支路数x；2）输入和输出电压确定变压器的匝数比N；3）ZVS和死区时间确定励磁电感Lm的选择范围；4）变换器的增益特性确定谐振电感Lr的选择范围；5）根据谐振频率fr确定谐振电容C1和C2的选择范围。

在 Matlab 中建立 Md，Mu，φd，φu和 fr的数学模型，给出边界条件，筛选结果。具体设计流程如图6所示。

图6 Multi-CLLC参数设计流程图Fig.6 The flow chart of multi-CLLC parameter design

结合器件制造工艺和成本要求，各主要谐振参数的选择范围限定如表1所示。

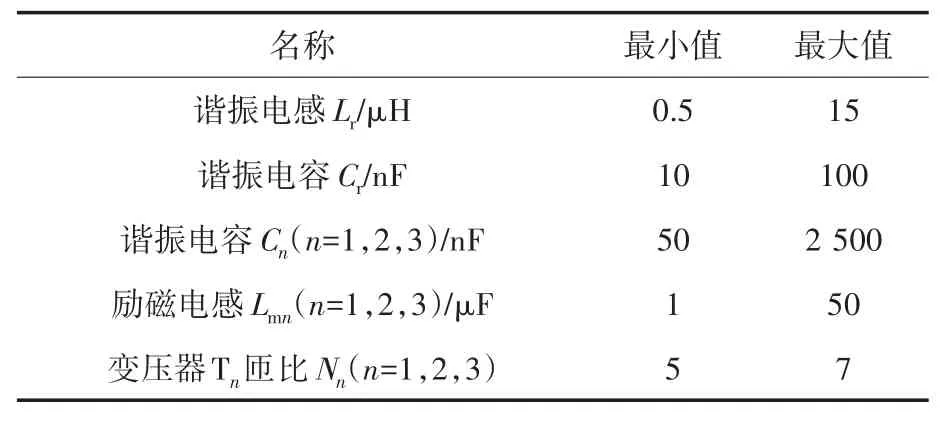
表1 参数取值范围Tab.1 List of components′parameters

结合PSIM仿真和效率计算，以变换器效率最高为目的进行进一步优化。最后，获得参数设计结果如表下：谐振电感Lr=4.7 μH，谐振电容Cr=7 nF，谐振电容Cn（n=1，2，3）=950 nF，励磁电感Lmn=9 μH，变压器Tn匝比Nn=6∶1。

3 磁集成设计

随着低压侧并联支路数的增加，电路中将引入多个变压器，不利于变换器功率密度及效率的提升。此外，在1 MHz高频情况下，漏感等寄生参数的影响显著，变压器参数一致性难以保证，从而导致变换器性能下降。采用平面磁集成技术可以解决以上问题，可以提高功率密度，改善变压器的一致性，磁集成变压器3D仿真模型如图7所示。

图7 磁集成变压器3D仿真模型Fig.7 3D simulation model of magnetically integrated transformer

铁心和铁心窗口区域的横截面积Ae和Aw分别表示为

式中：uin_min为变压器给定电压的最小值；ip_max，io分别为原边和副边绕组电流的最大值，jp，jo分别为对应的电流密度；kw为窗口填充系数；Bm为在fs处的最大磁密度。

根据变换器的额定工作频率，最终选择3F4铁心材料。同时，结合式（12）、式（13）和3D建模仿真结果，确定了铁心型号（E32-620）。

本文采用PCB绕组三明治绕法进一步降低漏感影响。高压侧绕组布置在上、下两层，低压侧绕组置于中间层，同时，为了避免气隙分布不均导致三个变压器漏感问题，采用了F型不对称磁芯结构，一定程度上保证三个变压器励磁与漏感参数的一致性，变压器绕组及磁芯如图8所示。

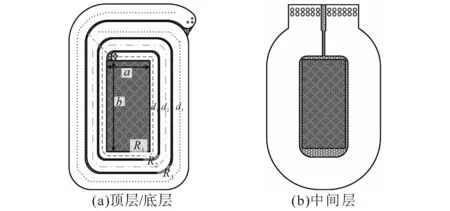
图8 PCB绕线模型Fig.8 The PCB winding wiring model

如图8所示，高压侧绕组采用不等宽线法。将线圈的等效串联阻抗最小化，减少变压器的绕组损耗。导线电阻可以通过下式来确定：

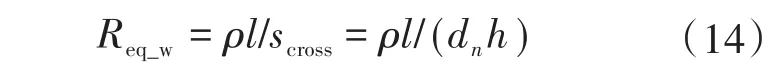
式中：dn为线圈Rn的宽度。

由式（14）可知，绕组的等效电阻Req_w主要与导体有效截面积scross、导体长度l和导体电阻率ρ有关。一般来说，采用铜作为PCB的布线材料，所以绕组的优化只需考虑长度l和有效截面积scross这两个因素。对于厚度h，由于高频时绕线电流具有明显的趋肤效应。在1 MHz情况下，导线厚度超过70 μm对有效截面积的影响趋于饱和；同时，增加厚度也会给工艺制造带来难度，导致制造成本增加。因此，综合考虑制作成本、难度和效率，选择70 μm的导线厚度。另一方面，绕组的宽度既受铁心窗口区域面积的限制，又受最大电流的限制。绕组的总电阻分别由R1，R2和R3表示：

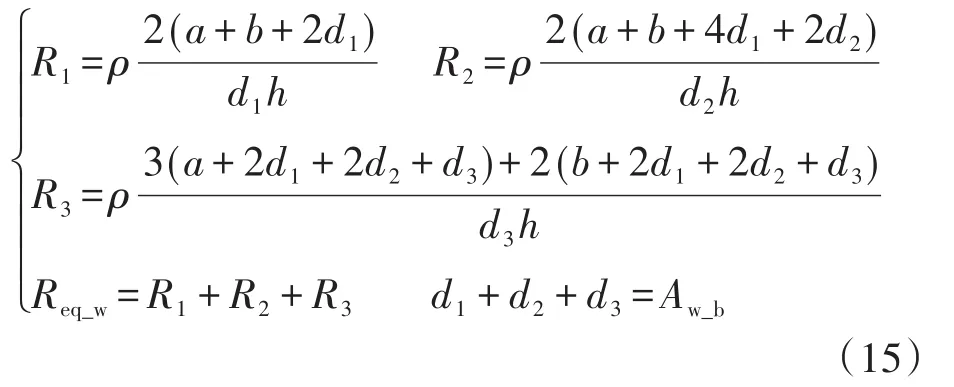
式中：a，b和Aw_b分别为磁芯相应的封装尺寸。

保证d1在给定的最小宽度与Aw_b/3之间，对Req_w求导。根据此d1处的最小等效电阻Req_w可以得到d2和d3的值。然后重新选择d1并重复上述步骤，完成Req_w的优化。

与传统等线宽方法进行比较，该布线方法有效改善了损耗，参数选择范围如表2所示。

表2 参数选择范围Tab.2 Parameter selection range

于低压侧绕组，采用多层并联方式来避免大电流引起的变压器过热。整体布线如图9所示。

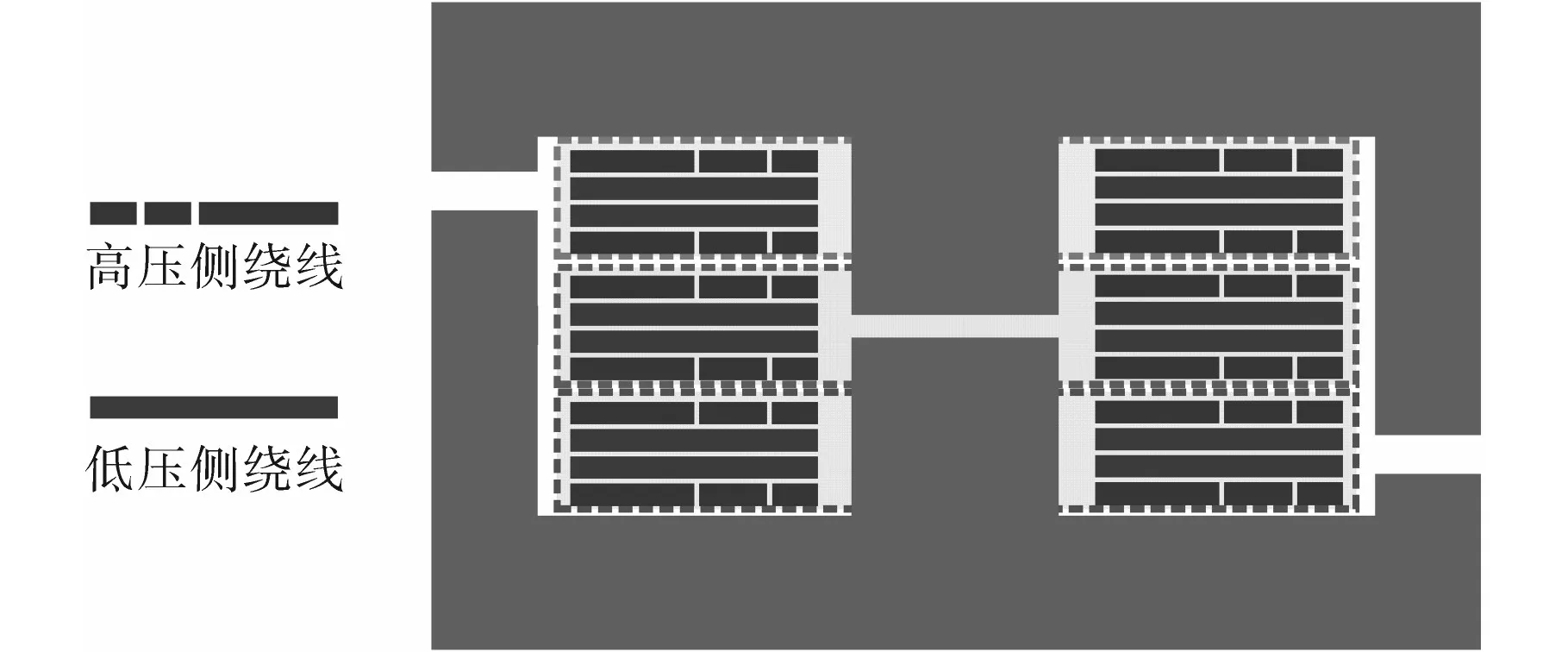
图9 变压器布线原理Fig.9 Winding layout of transformer

4 实验验证

为了验证拓扑的性能与理论分析的正确性，本文搭建了一台额定功率400 W的样机，如图10所示。其功率密度达到53 W/in3，并对样机进行了对应的实验验证。

图10 Multi-CLLC实验样机Fig.10 Multi-CLLC prototype

4.1 降压实验

降压模式的实验波形如图11所示。其中，图11a为开关频率为1 MHz的工作波形，图11b为700 kHz的工作波形。图11中，US1_G为S1的驱动电压，US1，US4x分别为开关管 S1和S4x的漏源电压；ir定义为谐振电流。400 V直流电压源作为高压侧输入。

图11 Multi-CLLC降压模式实验结果Fig.11 The multi-CLLC experimental results of step-down mode

从图11可知，在1 MHz的工作频率下，Multi-CLLC变换器工作在CCM模式，此时输出电压为20 V；在700 kHz情况下，变换器工作在DCM模式输出电压为22 V。这些实验结果证明了理论计算的准确性。同时，虚线中的波形显示，两种情况均实现了ZVS，这也与理论分析的结果一致。同时根据1 MHz情况下，低压侧变压器副边三路电流波形图12可知，输出侧三路电流i1，i2和i3近似实现均分，额定频率下每支路电流约为6 A。同时根据电流过零点与电压驱动的波形可以证明变换器低压侧开关管实现了ZCS。

图12 额定频率下支路电流曲线Fig.12 Branch current curves at rated frequency

上述实验结果表明，在降压模式下，变换器在标准化频率0.65～1.3的范围内调节可以实现0.9～1.2的标准化电压增益变化，验证了变换器的增益特性。

对应的实验效率曲线和理论计算效率的结果如图13所示。其中计算与实际实验的结果存在差异，这主要是由于实验中存在的一些震荡和部分被忽略的寄生参数所导致的。额定工作频率下变换器效率为92%，主要是由于100℃时低压侧GaN FETs导通电阻为30 mΩ，阻值较大，影响了变换器工作效率，其次副边三路并联电路的同步整流信号共用，导致无法独立微调各路的同步整流驱动死区，也产生了一部分附加损耗。

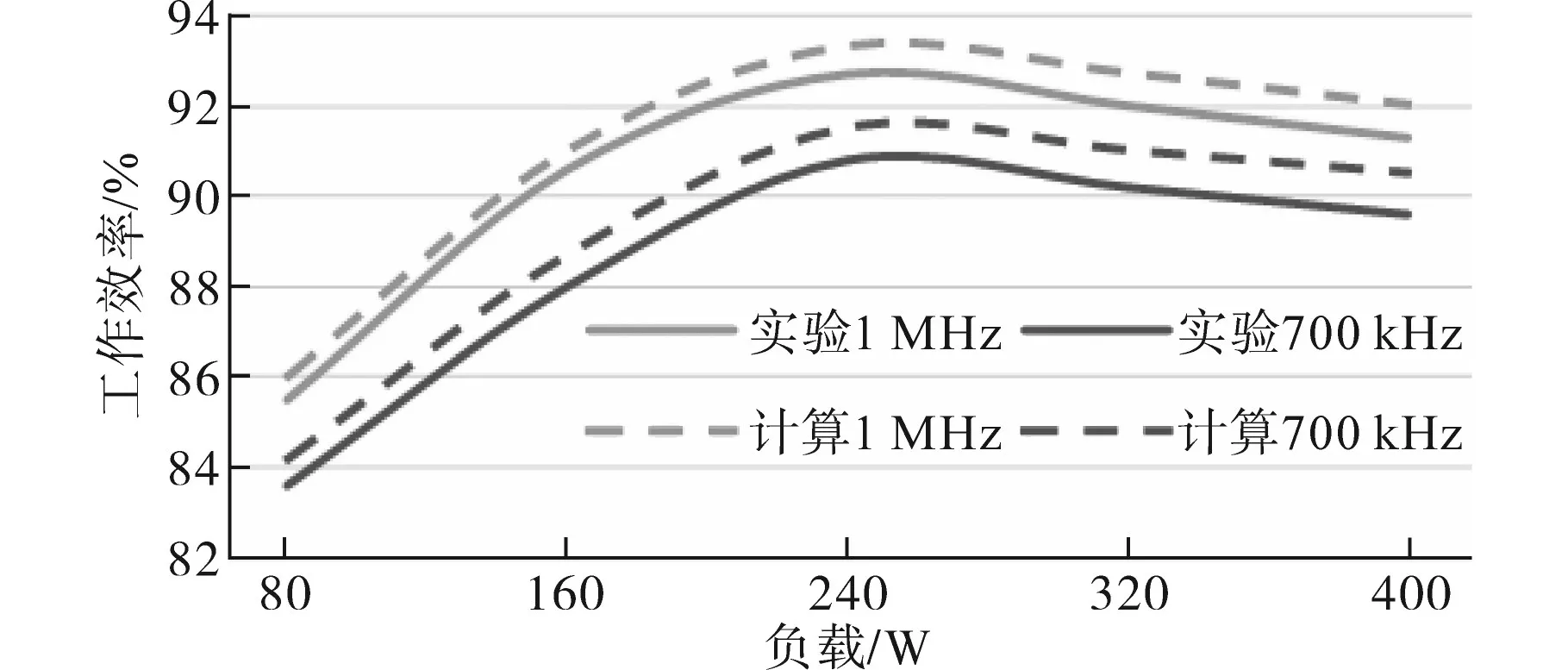
图13 Multi-CLLC降压模式效率曲线Fig.13 The multi-CLLC efficiency curves of step-down mode

4.2 升压实验

升压模式的实验结果如图14所示。与降压模式类似，1 MHz时Multi-CLLC变换器工作在CCM模式，此时低压输入电压为20.5 V，输出电压为400 V。由图14虚线圈内曲线可知升压模式同样实现了ZVS，相关效率曲线如图15所示。

图14 Multi-CLLC升压模式实验结果Fig.14 The multi-CLLC experimental results of step-up mode

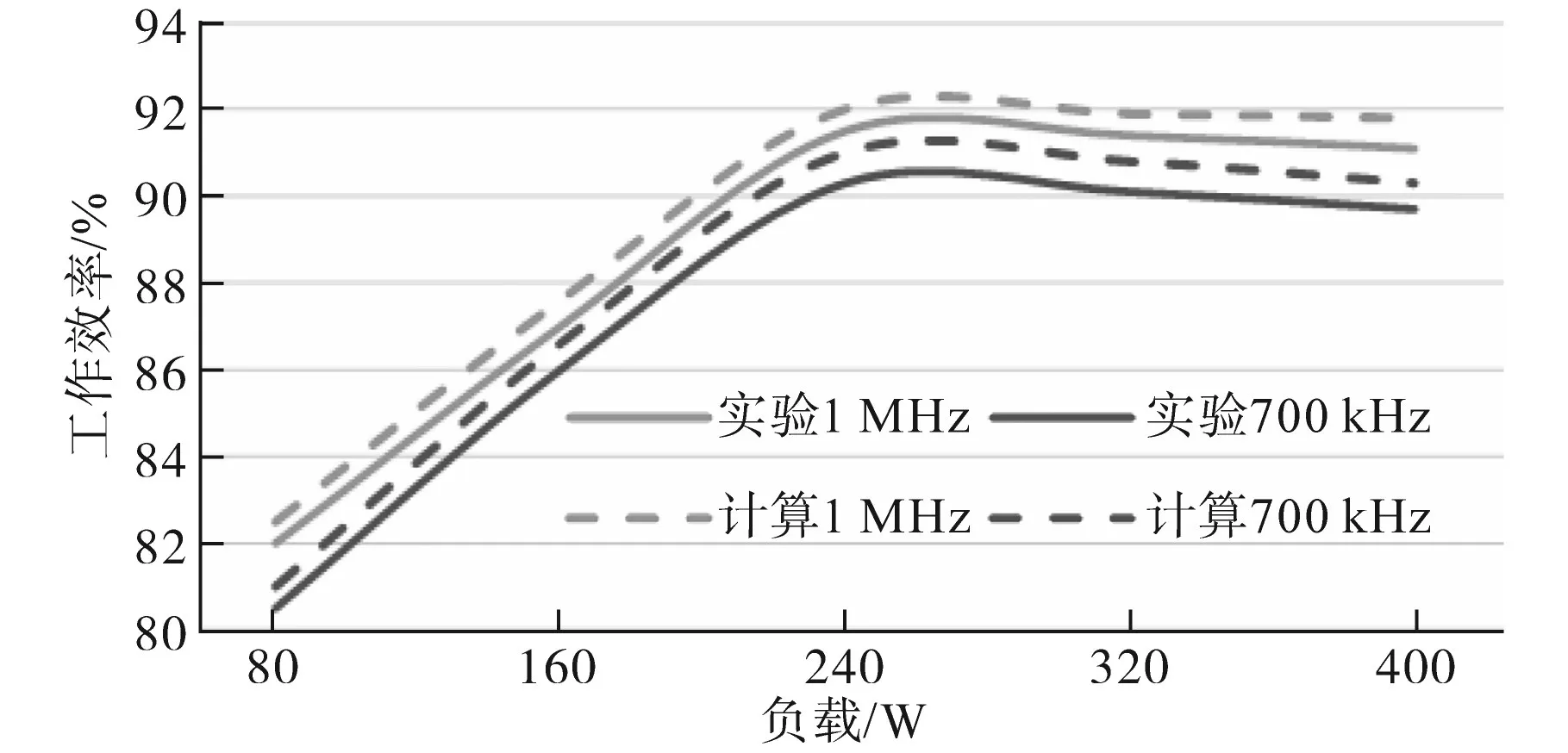
图15 Multi-CLLC升压模式效率曲线Fig.15 The multi-CLLC efficiency curves of step-up mode

5 结论

本文针对分布式储能应用，研究了一种改进型Multi-CLLC变换器，详细给出了Multi-CLLC的模态和特性分析、参数设计以及磁集成方法。结合GaN器件与磁集成技术，Multi-CLLC可以获得较好的增益特性和功率密度。此外，文章对PCB多线圈布线优化方法进行了分析。最后，搭建了一台400 W的实验样机并进行了实验验证。其功率密度53 W/in3。在400 W条件下，在700 kHz～1.2 MHz的频率范围内实现了电压增益在0.8～1.2的范围内调节。同时，变换器能维持较高的变换效率，降压模式下额定工况效率达到92%，升压模式下达到91%。较大的导通电阻和同步整流驱动死区限制了该变换器效率的进一步提升，相关改进研究有待进一步开展。