基于强繁殖NSGA-Ⅱ算法的柔性车间调度多目标优化*

朱旭东

(无锡工艺职业技术学院，江苏 宜兴 214200)

0 引言

根据市场的多变性和客户的多样性需求，产品的多样化和小批量生产成了生产制造行业的主流模式，传统单一品种大批量生产的刚性车间已经无法满足市场需求，使得柔性制造车间不断涌现。对于柔性作业车间，产品的每道工序可由多个机器加工而成，因此存在产品的加工顺序和工序的机器分配等诸多调度问题[1]。不同的调度方案对应的完工时间、机器能耗、机器负荷也不同，因此研究车间调度问题具有重要的实际意义。

根据优化目标的数量，可以将柔性车间调度问题分为单目标调度问题和多目标调度问题。单目标调度研究主要集中在最小化完工时间这一目标上，文献[2]在差分进化算法中引入了一种新的转化方法，使其能够有效求解柔性车间调度问题，实现了对柔性车间完工时间的优化。文献[3]以最小化完工时间为车间优化目标，在算法中引入了反向学习策略和Metropolis准则，实验验证了该方法在车间调度中的优越性。多目标优化处理的多个目标间一般存在冲突问题，一般包括先验法和后验法两类。先验法是指根据先验知识为每个目标线性加权得到单个目标，文献[4]针对柔性车间多目标调度问题，提出了混合TS算法的求解方法。文献[5]针对质检引起的完工时间延迟和耗能升高问题，提出了改进头脑风暴的求解方法，在保证交付时间约束下降低了车间能耗。先验法中精准确定每个目标的权重非常困难，需要大量经验的积累，而且基于聚合的方法无法解决Pareto解集非凸的问题，因此后验法成为了解决柔性车间多目标优化的热点方法。文献[6]设计了新的适应度分配策略，有效解决了柔性车间完工时间、机器负荷等目标的优化。文献[7]在粒子群算法中引入了邻域搜索算法和无需半径共享的小生境技术，实验验证了该方法在完工时间、车间总负荷、均负荷等多目标优化中的优越性。基于后验法的柔性车间调度方法很多，但是多数在全局搜索和局部开发上存在矛盾，因此两者的平衡是当前研究的一个重要方向。

针对柔性车间调度的多目标优化问题，建立了以减小完工时间、机器总负荷和车间能耗为目标的多目标优化模型，提出了强繁殖NSGA-Ⅱ算法的模型求解方法，实现了减小完工时间、机器负荷、车间能耗的优化目标。

1 柔性车间调度问题描述与建模

1.1 问题描述

柔性车间调度问题描述如下：车间需加工N个工件，记为{J1,J2,…,JN}；每个工件由若干个工序加工而成，以工件Ji为例其加工工序可记为Ji={Oi1,Oi2,…,Oij}，式中Oij为工件Ji的第j道工序；车间可提供的机器设备为K个，记为{M1,M2,…,MK}，每道工序Oij对应一个可选机器集合，记为Mij。需解决的问题是，为各道工序选择合适的加工设备、合理的加工时间，在满足生产工艺约束的前提下，实现完工时间最小、机器总负荷最小、总能耗最低等目标。

柔性车间调度问题需满足的约束条件包括：

(1)在同一时刻，每个机器最多加工一道工序；

(2)工件之间的加工顺序完全独立，但是同一零件的工序间必须满足顺序要求；

(3)各工序开始加工后，不允许中断。

柔性车间可以分为完全柔性车间和部分柔性车间[8]，完全柔性车间是指每道工序都可由车间内任意机器加工，部分柔性车间是指每道工序只能由车间内部分机器加工，其中部分柔性车间更加普遍，因此本文研究的是部分柔性车间调度问题。

1.2 柔性车间调度优化模型

本文针对柔性车间的调度问题，设置3个优化目标，分别为完工时间最短、机器总负荷最小、车间总能耗最少。

(1)完工时间最短。工件的完工时间是指工件最后一道工序的完工时间，而车间的完工时间是指所有工件中最晚的完工时间，为：

(1)

式中，Ci为工件Ji的完工时间，f1为车间完工时间优化的目标函数。

(2)机器总负荷最小。车间内机器负荷随调度方案的变化而变化，减小车间内机器总负荷可以有效提高机器的使用寿命，因此以减小车间内机器总负荷为一个优化目标，即：

(2)

式中，f2为车间机器总负荷最小化目标函数，hi为工件Ji的工序数量，tijk为工序Oij在机器Mk上的加工时间，xijk为工序Oij在机器Mk上的加工标识，即：

(3)车间能耗最少。柔性生产车间的能耗包括加工能耗、空载能耗、转运能耗和固定能耗等，为：

(3)

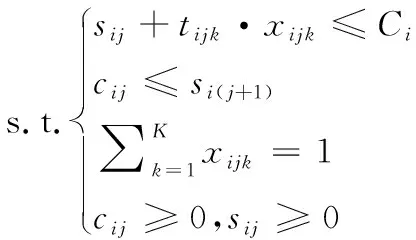
(4)

式中，sij为工序Oij的开始时间，Ci为工件Ji的完工时间，cij为工序Oij的结束时间，Cmax=maxCi为车间完工时间。

式(4)中第1式表示工序Oij的结束时间应小于工件Ji的完工时间，第2式表示工序Oij的结束时间应小于工序Oi(j+1)的开始时间，第3式表示工序Oij只需加工一次，第4式表示工序Oij的开始时间和结束时间均应为正值。

1.3 编码与甘特图解码方法

在柔性车间调度问题中有两个问题需要解决，一是确定各工序的生产顺序，二是确定各工序的加工机器。为了同时解决这两个问题，本文使用双基因链编码方式，基因链中的基因长度与工件的所有工序数量一致。第一条基因链用于确定工序加工顺序，第二条基因链用于确定各工序对应的机器。

以3个工件加工为例，每个工件具有3道加工工序，可使用的生产设备具有3台，分别记为M1、M2、M3。假设某染色体编码方式如图1所示。

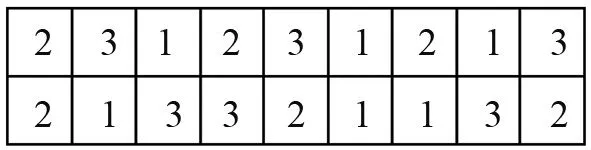
图1 染色体编码方式

图1中第一条基因链确定了工序的加工顺序，工件2具有3道工序，因此在第一条基因链中出现了3次，第1次出现表示工件2的第1道工序。按照这种规定，第一条基因链对应的工序顺序为：O21O31O11O22O32O12O23O13O33，对应的机器为M2M1M3M3M2M1M1M3M2。

甘特图可以对以上编码和解码结果进行更加直观的表达，图1中的染色体使用甘特图可表示如图2所示。

图2 图1对应的甘特图

由图2可以直观看出各工序的加工顺序、各工序使用的加工机器、各工序的加工耗时、总完工时间等。因此，柔性车间的调度结果一般使用甘特图给出。

2 强繁殖NSGA-Ⅱ求解算法

2.1 强繁殖NSGA-Ⅱ算法构造思路

NSGA-Ⅱ算法原理可参考文献[9-10]，这里不再赘述。由于NSGA-Ⅱ算法沿袭了遗传算法中的交叉、变异、自然选择等操作思路，因此遗传算法存在的算法收敛性与个体多样性之间的矛盾，NSGA-Ⅱ算法也必然存在[11]。为了克服算法的这一缺陷，有效平衡NSGA-Ⅱ算法的多样性和收敛性，本文提出了具有强繁殖能力的NSGA-Ⅱ算法。

强繁殖NSGA-Ⅱ算法的构造思路为，首先定义染色体的繁殖能力，根据繁殖能力将染色体分为强繁殖个体和普通个体。将强繁殖个体(繁殖能力大于均值)划为一个子群，将普通个体划分为一个子群。其中强繁殖子群具有较强的繁殖能力，使用传统的交叉变异方式即可；普通子群的繁殖能力较弱，使用染色体变化较大的改进交叉变异方法。两个子群每进化5代进行一次混合，并重新划分子群。

2.2 染色体繁殖能力

染色体的繁殖能力以其遗传操作后的繁殖能力为标准进行衡量。将染色体规模记为N，以染色体n为例对繁殖能力度量方法进行介绍。

步骤2：将测试染色体逐个与染色体n进行交叉操作，交叉操作使用传统交叉方式，传统交叉方法在后文中明确；

步骤3：染色体n交叉后，若2个子代个体中存在支配染色体n的个体，说明实现了染色体进化，此时染色体n的繁殖能力+1；若2个子代个体均无法支配染色体n，说明染色体未进化，此时染色体n的繁殖能力维持不变；

步骤4：当染色体n与所有测试染色体完成交叉测试后，计算染色体n的繁殖能力，迭代过程结束。

2.3 种群分割与遗传操作

将所有染色体分为两个种群，繁殖能力大于均值的个体属于强繁殖能力种群；繁殖能力低于均值的属于普通种群。下面依据两个种群的特点，为两个种群施加不同的遗传操作。

(1)强繁殖能力种群的遗传操作。强繁殖能力种群的染色体繁殖能力较强，使用传统的交叉变异方式就能够保持种群的全局优势。柔性车间调度问题的遗传操作分为工序遗传操作和机器遗传操作。工序遗传操作使用传统的POX交叉和插入变异方法[12]。机器遗传操作使用单点交叉和单点变异。

(2)普通种群的遗传操作。普通种群繁殖能力相对较弱，因此设置遗传操作时，采用使染色体变化较大的操作方法，强制性提高染色体的繁殖能力。

普通种群工序排序使用的交叉方式为改进POX交叉方式，如图3a所示。改进POX交叉的执行方法为：将工件按照大致等量的原则分为两组，图3a中将4个工件分为两组，其中{2，3}为一组，{1，4}为一组。父代1的1、4基因保持不变遗传给子代2，父代2的2、3基按照顺序左移一个基因位并嵌入到子代2的空位中。父代2的2、3基因位保持不变遗传给子代1，父代1的1、4基因按照顺序左移一个基因位嵌入到子代1的空位中。

工序排序的变异方式为基因串逆序变异方式，如图3b所示。具体操作方法为：随机产生两个基因位，将两个基因位之间的基因进行逆序排列。图3b中随机产生的基因位为4和9，将两个基因位之间的基因逆序排列后放入到染色体中，即实现了基因串逆序变异。

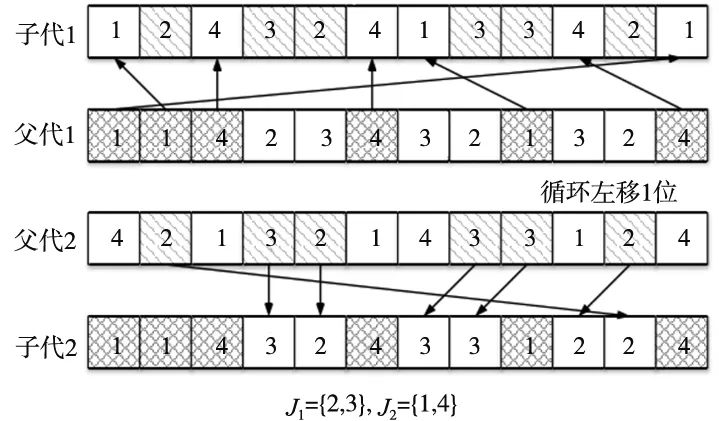
(a) 改进POX交叉操作

(b) 基因逆序变异操作图3 工序的遗传操作

机器基因链的交叉操作使用均匀交叉方法，如图4a所示。具体执行方法为：随机选择若干个基因位，父代1和父代2被选基因位的基因保持不变，其余基因位的基因按照对应关系进行交叉，即可得到子代1和子代2。

机器基因链的变异操作使用定向变异方法，如图4b所示。首先随机选择两个基因位，图4b中随机选择了基因位4和9。而后从两个基因位的可选机器集种随机选择一个机器，并替换到原基因，图4b中的基因位4，使用机器2替换原机器5，基因位9，使用机器6替换机器1。

(a) 均匀交叉操作

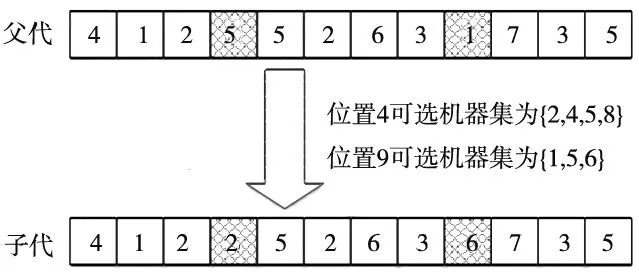
(b) 定向变异操作图4 机器的遗传操作

在普通种群中，设置一个随机数p∈(0,1)，再设置一个随机数阈值p0，当p>p0时针对工序基因链施加遗传操作，当p≤p0时针对机器基因链施加遗传操作。强繁殖子群与普通子群之间的交流方式为融合交流，也即每迭代5次，将强繁殖子群和普通子群进行混合，再次计算各染色体的繁殖能力，并进行种群的重新划分。

2.4 强繁殖NSGA-Ⅱ算法步骤

根据强繁殖NSGA-Ⅱ算法的构造思路，得到强繁殖NSGA-Ⅱ算法步骤如下：

步骤1：设置算法参数，即染色体规模、交叉概率、变异概率、最大迭代次数等；

步骤2：染色体以随机方式进行初始化；

步骤3：计算各染色体的繁殖能力，并依据繁殖能力将染色体划分为强繁殖子群和普通子群；

步骤4：强繁殖子群和普通子群按照各自的方式进行交叉变异和选择，每迭代一次则迭代次数+1；

步骤5：判断迭代次数是否达到最大值，若否则判断迭代次数是否为5的倍数，若为5的倍数则转至步骤3，若不为5的倍数则转至步骤4；若迭代次数达到了上限，则算法结束。

3 柔性车间调度实验

3.1 柔性车间调度设置

本文研究的车间调度算例中需生产的工件为8个，车间可提供的生产设备为8台，各工件的加工工序不等，不同工序在各生产设备上的加工时间如表1所示。

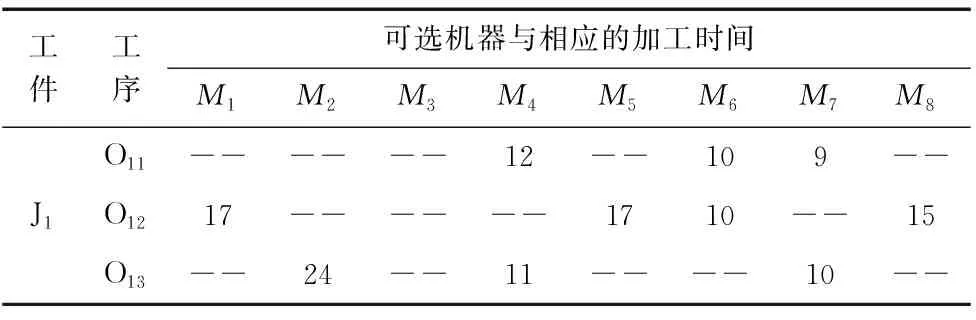
表1 工序加工时间表 (h)

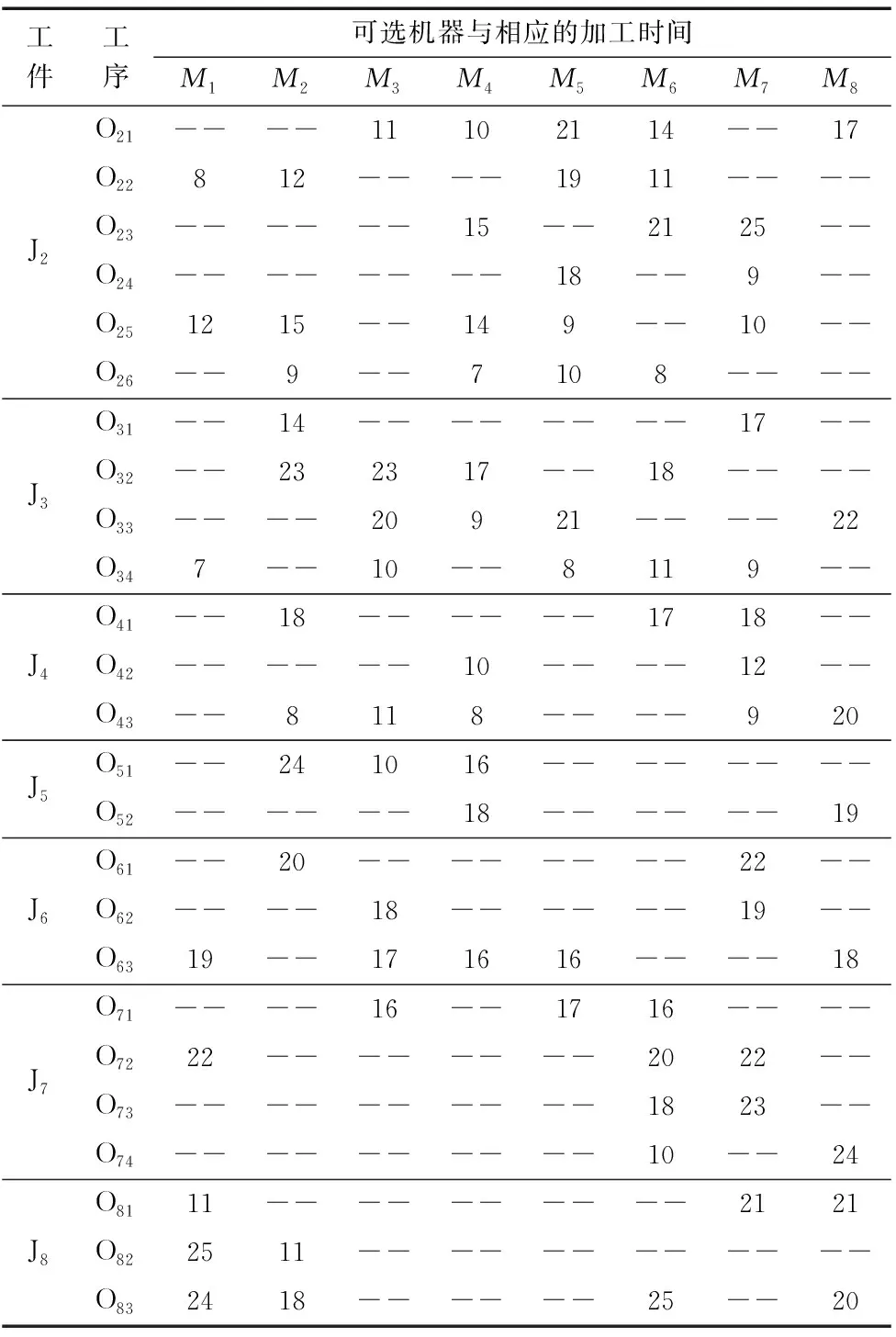
续表

表1中数字表示工序在对应机器上的加工时间，单位为小时，“--”表示工序无法在相应机器上加工。各机器加工功率和空载功率如表2所示。

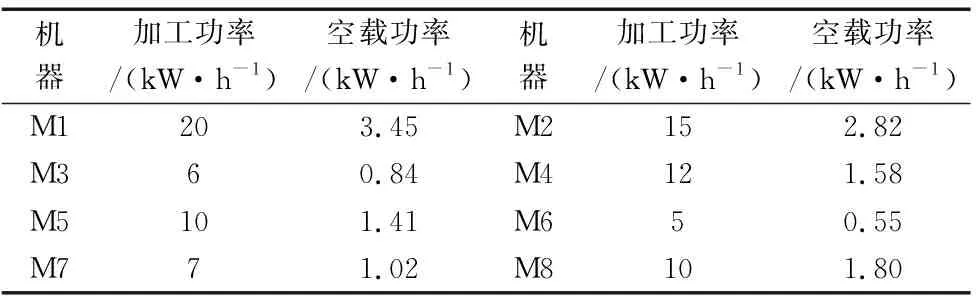
表2 机器的加工功率与空载功率

3.2 调度结果与分析

强繁殖NSGA-Ⅱ算法的参数设置为：染色体规模为100，最大迭代次数为100，交叉概率设置为0.5，变异概率设置为0.1。为了进行对比，同时使用传统NSGA-Ⅱ算法进行柔性车间调度优化，算法参数设置与强繁殖NSGA-Ⅱ算法一致。两种算法的车间调度结果如图5所示。

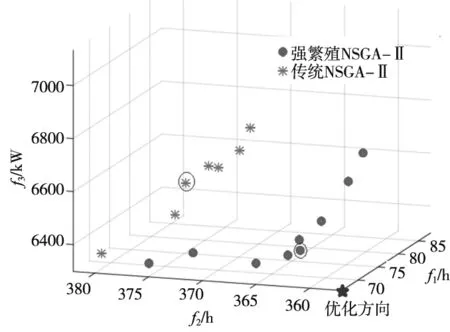
图5 两种遗传算法得到的Pareto解集

本文的3个优化目标均为最小化优化目标，对应到图5所示的3维空间中，图中蓝色“☆”位置为本文的优化方向，因此强繁殖NSGA-Ⅱ算法的Pareto解集明显优于传统NSGA-Ⅱ算法的Pareto解集。这是因为强繁殖NSGA-Ⅱ算法中按照染色液的繁殖能力，将染色体划分为2个种群，两个种群按照各自的特点设置遗传操作，有效提高了算法繁殖能力和进化能力，因此解集优于传统NSGA-Ⅱ算法的Pareto解集。

按照各优化目标重要度折中的原则，从两个Pareto解集中选择居中的两个解进行对比，被选择的解为图5中圆圈圈出的解。两个解对应的生产甘特图如图6所示。

图6 两种算法解的甘特图

统计图6两个解的完工时间、机器总负荷、车间能耗，结果如表3所示。

表3 两个解的调度统计参数

结合图6和表3可以看出，从传统NSGA-Ⅱ算法和强繁殖NSGA-Ⅱ算法中选择的折中解，传统NSGA-Ⅱ算法解的完工时间为81 h，机器总负荷为378 h，车间能耗为6460 kW；强繁殖NSGA-Ⅱ算法解的完工时间为70 h，机器总负荷为364 h，车间能耗为6380 kW，以上参数均小于传统NSGA-Ⅱ解的参数。从表象上看，图6中强繁殖NSGA-Ⅱ解对应甘特图中机器工作量分配更加平均，而传统NSGA-Ⅱ解的甘特图中机器工作量分配相对集中，因此强繁殖NSGA-Ⅱ解的调度结果更优。从算法原理角度讲，强繁殖NSGA-Ⅱ算法按照染色液的繁殖能力，将染色体划分为2个种群，两个种群按照各自的特点设置遗传操作，有效提高了算法繁殖能力和进化能力。以上柔性车间的调度结果和分析验证了强繁殖NSGA-Ⅱ算法在柔性车间调度中的有效性和优越性。

4 结论

本文研究了柔性车间的调度优化问题，建立了车间调度的多目标优化模型，在传统NSGA-Ⅱ算法中引入了强繁殖度量、多种群遗传等操作，有效改善了算法的优化能力，经验证得出以下结论：

(1)与传统NSGA-Ⅱ算法相比，强繁殖NSGA-Ⅱ算法的解集质量更高，优化能力更好；

(2)强繁殖能力NSGA-Ⅱ算法应用于柔性车间调度多目标优化是有效的，可以有效减少完工时间、机器总负荷和车间能耗。