素数阶群上基于非对称对的身份基环签名

侯红霞，张明瑞，赵艳琦，董晓丽,3

（1.西安邮电大学网络空间安全学院，陕西 西安 710121；2.陕西师范大学计算机科学学院，陕西 西安 710061；3.广西密码学与信息安全重点实验室，广西 桂林 541004）

1 引言

环签名的概念是由Rivest 等[1]于2001 年提出的。在环签名中，环中的任意成员都能代表整个环对消息进行签名，签名验证者仅知道签名来自环，但却不能确定具体的签名者。环签名中没有管理员，没有环的建立和撤销过程，因此真实的签名者对于验证者而言是无条件匿名的。

为了简化传统公钥基础设施中的证书管理问题，Shamir[2]于1984 年引入了身份基公钥密码体制。在身份基密码体制中，用户的公钥可以是标识该用户身份的任意二进制串，比如E-mail 地址等；对应的私钥则是由一个可信任的私钥生成中心（PKG,private key generator）根据该用户的身份生成的。因此，PKG 不需要保存已发布的证书列表，每个用户仅需保存系统参数而不需要保存其他用户的公钥证书。

身份基环签名将身份基公钥密码体制和环签名技术相融合，既实现了匿名性、不可伪造性，又避免了用户证书的管理。作为实现匿名性的一个重要的密码学原语，身份基环签名在许多场合（如电子选举、电子现金、区块链技术、车联网等[3-8]）中有重要的应用。

自从Zhang 等[9]正式给出身份基环签名的概念后，许多身份基环签名方案及其变种被相继提出[10-16]。然而，这些方案的安全性都是在随机预言机模型下证明的。在随机预言机模型中，哈希函数被作为一个完全随机的理想化模型，这是一个非常强的假设。已有文献[17]表明，在随机预言机模型下被证明安全的方案在实际应用中可能并不安全。因此，设计标准模型下可证明安全的身份基环签名方案更具实际意义。2006 年，Au 等[18]在标准模型下提出了2 个身份基环签名方案，但遗憾的是，这2 个方案后来被证明并不能满足环签名的安全需求。此后，有许多工作致力于构造标准模型下高效安全的身份基环签名方案。文献[19-20]从节约通信成本和提高计算效率的角度出发，分别在标准模型下提出了改进的身份基环签名方案，但遗憾的是，这2 个方案之后被证明不安全。2012 年，文献[21]给出了一个标准模型下具有固定签名长度的身份基环签名方案，但该方案被指出有漏洞。2013 年，通过分析分层身份基加密方案与身份基环签名方案之间的联系，Au 等[22]在标准模型下提出了一个身份基环签名方案。2018 年，基于Au 等[22]方案，赵艳琦等[23]在标准模型下构造了一个新的身份基环签名方案。方案[22-23]在安全性证明时都采用了对偶系统加密技术，从而在标准模型下都达到了全安全性和完全匿名性。对偶系统加密技术为安全性归约证明开辟了一条新思路。然而，这2 个方案都是在合数阶双线性群上构造的，因而实现效率都很低。已有文献[24]指出，阶数n为160 bit 的素数阶群具有与阶数n为1 024 bit 的合数阶群同样的安全水平，合数阶群上的双线性对运算要比素数阶群上的对运算慢许多。因此，在素数阶群上设计高效安全的环签名方案具有重要的实际意义。文献[22]也将此作为一个公开问题提出。

Ramanna 等[25]在非对称双线性对环境中提出了一些Waters 对偶系统原语[26]的变形机制。许多研究结果[27-29]已表明，相比于对称双线性对运算，非对称双线性对运算更加快速和紧致。基于文献[22-23,25]的工作，本文给出了一种在素数阶群上构造身份基环签名方案的方法。在素数阶群上基于非对称双线性对构造了一个高效的身份基环签名方案。该方案可以抵抗适应性选择身份攻击和适应性选择消息攻击。通过采用对偶系统加密技术，该方案的安全性被归约到素数阶群上非对称对环境中的3 个困难性假设。实验结果表明，与已有的基于对偶系统的身份基环签名方案相比较，本文方案在效率方面更具优势。

2 预备知识

2.1 符号说明

本文中，κ表示安全参数，negl(κ)表示一个关于κ的可忽略函数，表示x均匀随机地取自集合X，|R|表示集合R的基，[n] 表示集合{1,2,…,n}，ε表示一个可忽略的参数。

2.2 非对称双线性对

令(G1,G2,GT)分别是3 个阶为素数p的循环群，其中和分别表示由P1和P2生成的加法群，GT是乘法群。

双线性对e:G1×G2→GT是满足以下性质的映射。

1) 双线性。对于P1,Q1∈G1和P2,Q2∈G2，有

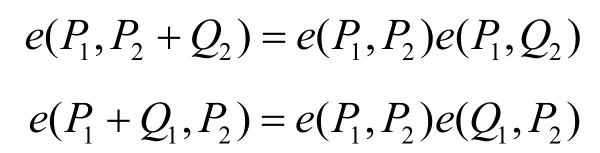
2) 非退化性。e(P1,P2)≠1∈GT。

3) 有效可计算性。对于任意的P∈G1和Q∈G2，存在一个有效的算法计算e(P,Q)。

当G1=G2时，双线性映射被称为对称或类型1 双线性映射，否则被称为非对称双线性映射。非对称双线性映射进一步可分为类型2 和类型3非对称双线性映射。类型2 非对称双线性映射是指由G1到G2或由G2到G1存在一个有效的可计算同构，而类型3 非对称双线性映射则不存在这样的同构。对于S1∈G1和S2∈G2，文中用S1～S2表示S1（以P1为底）和S2（以P2为底）具有相同的离散对数。

2.3 复杂性假设

判定性 Diffie-Hellman（DDH,decision Diffie-Hellman）假设[25]。令P1,P2分别是群G1,G2的随机生成元，x1,x2,

G1中的DDH 问题（记为DDH1）是指给定(P1,x1P1,x2P1,P2,Z1=(x1x2+c)P1)，判定c=0还是

令B是一个输出为0 或1 的多项式时间（PPT,probabilistic polynomial time）算法。定义B解决DDH1 问题的优势为

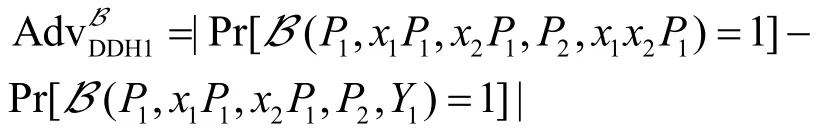
如果对于任意敌手B，其运行时间至多为t，解决 DDH1 问题的优势为≤ε，则称(ε,t)-DDH1假设成立。

G2中的DDH 假设（记为DDH2）定义类似。

DDH2v 假设[25]。令P1,P2分别是群G1,G2的随机生成元，

DDH2v 问题是指给定(P1,dP1,dzP1,zx1P1,P2,dP2,x1P2,x2P2,Z2=(x1x2+c)P2)，判定c=0还是

令B是一个输出为0 或1 的PPT 算法。定义B解决DDH2v 问题的优势为

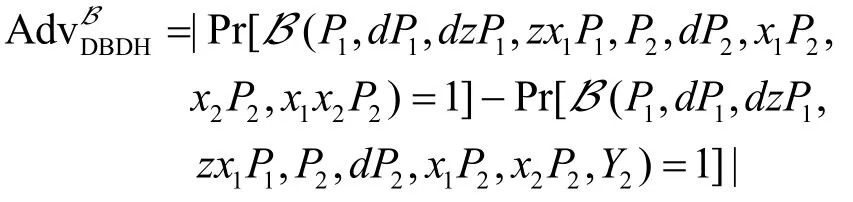
如果对于任意敌手B，其运行时间至多为t，解决DDH2v 问题的优势为≤ε，则称(ε,t)-DDH2v 假设成立。

判定性双线性Diffie-Hellman（DBDH,decision bilinear Diffie-Hellman）假设[25]。令P1,P2分别是群G1,G2的随机生成元，

DBDH 问题是指给定(P1,x1P1,x2P1,x3P1,P2,，判定还是

令B是一个输出为0 或1 的PPT 算法。定义B解决DBDH 问题的优势为

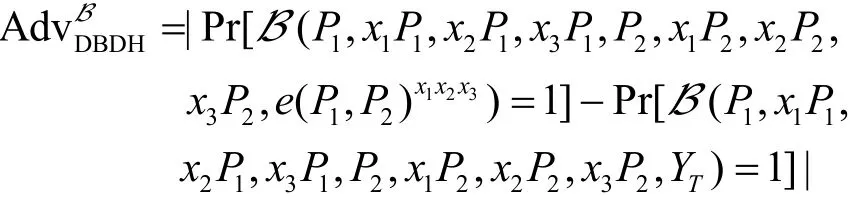
如果对于任意敌手B，其运行时间至多为t，解决 DBDH 问题的优势为，则称(ε,t)-DBDH 假设成立。

2.4 安全模型

定义1一个(1,n) 身份基环签名方案由以下4 个PPT 算法组成。

Setup。该算法由PKG 运行，输入一个安全参数κ，输出主密钥MSK 和系统公开参数Params。

Extract。对于身份ID，该算法输入主密钥MSK，输出身份ID 所对应的私钥SKID。

Sign。输入系统公开参数Params、身份集Ring={ID1,…,IDn]、消息m以及用户私钥{SKID|ID ∈Ring}，输出一个(1,n) 身份基环签名σ。

Verify。输入系统公开参数Params、n个用户的身份集Ring={ID1,…,IDn}、消息m以及环签名σ，输出Valid 或Invalid。

一个安全的(1,n) 身份基环签名方案应满足不可伪造性和匿名性。

定义2不可伪造性。如果没有多项式时间敌手能以不可忽略的优势赢得以下游戏，一个(1,n)身份基环签名方案在适应性选择消息攻击和适应性选择身份攻击下是不可伪造的。

该游戏在敌手A与挑战者C之间进行。

1) 输入安全参数κ，挑战者C运行Setup 算法，然后将系统公开参数Params 发送给敌手A。

2) 通过访问下述预言机，敌手A在多项式时间内适应性地向挑战者C发起以下询问。

密钥提取预言机（EO,extraction oracle）：输入身份ID，SKID←Extract(params,ID)被返回给敌手A。

签名预言机（SO,signing oracle）：敌手A选取一个身份集Ring={ID1,…,IDn}和消息m，签名预言机会返回一个有效的(1,n) 身份基环签名σ给A。此过程中，签名预言机可以询问密钥提取预言机。

3) 最后，A输出(Ring*,m*,σ*)，且(Ring*,m*)没有在之前的签名询问中出现过，同时对于环Ring*中的任意身份ID ∈Ring*，不允许A做密钥提取询问。

如果Verify(Ring*,m*,σ*)的输出结果为Valid，则A赢得该游戏。定义敌手A的获胜优势为

定义3匿名性。当且仅当以下条件被满足，一个(1,n)身份基环签名方案是无条件匿名的。

给定任意身份集Ring={ID1,…,IDn}，消息m以及环签名σ，即使以无限的计算能力，任意敌手都不能以优于随机猜测的概率识别出真实的签名者。换句话说，敌手A仅能以不高于的概率输出真实签名者的身份。

2.5 敌手模型

存在2 种类型的签名和密钥：正常类型，记为type-N；半功能类型，记为type-S。type-S 类型的签名和密钥仅在安全性证明中使用，并不会出现在真实的签名方案中。

根据签名的类型可将敌手划分为2 种类型。

type-S 伪造者：如果敌手为type-S，这种情况下，模拟器仅输出type-N 签名和密钥。

type-N 伪造者：如果敌手为type-N，这种情况下，模拟器需要使用game-hopping 技术在敌手未察觉的情况下将签名和密钥逐步由type-N 转变为type-S。

3 基于非对称对的身份基环签名方案

3.1 方案构造

Setup。令e:G1×G2→GT是一个类型3 非对称双线性映射，其中G1=P1和G2=P2都是阶为素数p的加法群。随机选取参数，使V2=vP2，，τP2=V2+（τ=v+av′）。H0:{0,1}*→Zp，H1:{0,1}*×{0,1}*→Zp是2 个抗碰撞哈希函数。PKG 随机选取α∈Zp，Q1,W1,U1∈G1，Q2,W2,U2∈G2且Q1～Q2，W1～W2，U1～U2。系统主密钥为MSK=αP2，系统公开参数为Params={P1,aP1,τP1,Q1,W1,U1,e(P1,P2)α,H0,H1}。

Extract。为了生成身份ID ∈{0,1}ℓ的用户私钥，该算法随机选取和标签计算

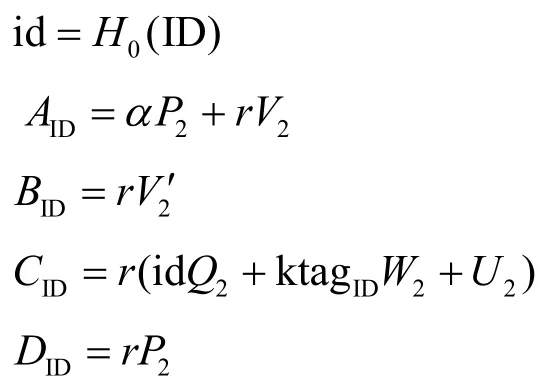
算法输出SKID=(AID,BID,CID,DID)作为身份ID 的用户私钥，并秘密发送SKID和{ktagID,P2,V2,Q2,W2,U2}给用户ID。

Sign。令环Ring={ID1,…,IDn}为包含n个身份的身份集。假设环Ring 中的一个用户ID，不失一般性，假设ID 是环Ring 的第π个用户（π∈[n]），即IDπ=ID。为了生成消息m∈{0,1}*的环签名，该算法分别计算idi=H0(IDi)（i∈[n]）以及M=H1(m,Ring)，然后执行以下步骤。

1) 随机选取λi,ri（i∈[n]，令ktagπ=ktagID）使其满足限制和

2) 对于i∈[n]，有以下结论成立。

当i≠π时，有

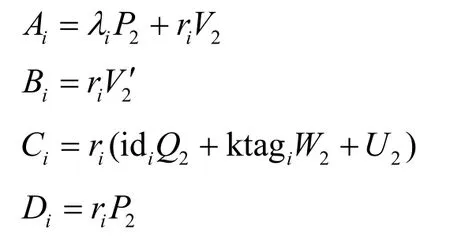
当i=π时，有

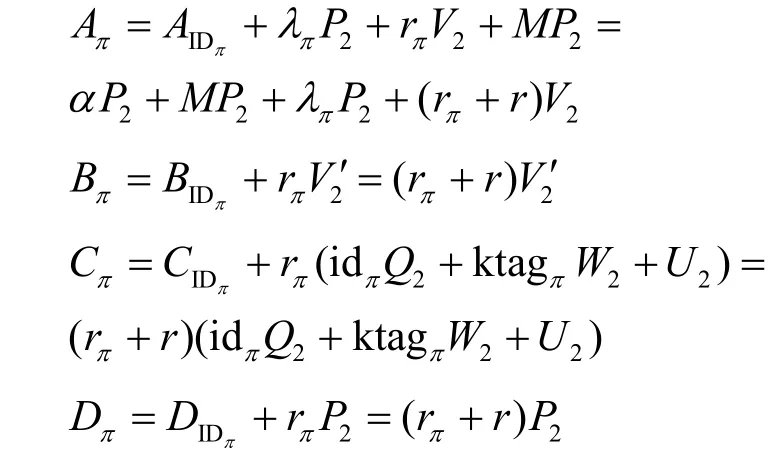
3) 输出签名σ=

Verify。在收到消息m的环签名σ={Ai,Bi,Ci,Di,后，验证者先计算idi=H0(IDi)（i∈[n]）和M=H1(m,Ring)；然后随机选取s,ctag1,…,（其 中 ctagi≠ktagi,i∈[n]）并计算T1=sP1,T2=asP1,T3=-sτ P1+sW1,T4,i=s(idiQ1+ctagiW1+U1)；最后验证者检验式(1)是否成立。

3.2 正确性

方案的正确性成立，是因为

4 安全性证明

本文方案的安全性采用对偶系统加密技术进行证明，为此需定义2 个额外的结构，即半功能密钥和半功能签名，半功能密钥和半功能签名不会出现在真实的签名方案中，仅用于方案的安全性证明。

半功能密钥。若身份ID 的正常密钥为SKID=，则其半功能密钥被设置为DID=)，其中

半功能签名。对于环Ring={ID1,…,IDπ,IDn}，若签名算法输出的正常签名为σ′=，则其半功能签名σ设置为，其余元素与σ′中的元素相同，即

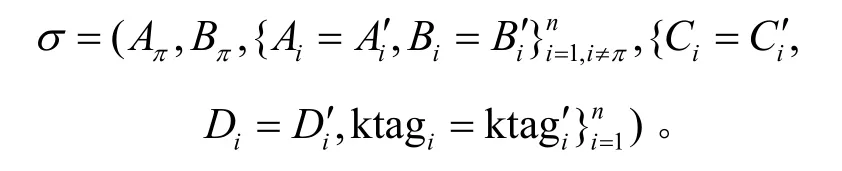
定理1若假设DDH1、DDH2v 和DBDH 成立，则3.1 节所构造的方案是不可伪造的。

证明为了证明本文方案在 type-S 伪造者和type-N 攻击下是不可伪造的，考虑下面2 种情况。

情况1若敌手A能输出一个type-S 的伪造，则可构造一个能利用敌手A的能力攻破假设DDH1 的模拟器B。

换句话说，模拟器B的目的是在收到一个DDH1 实例(P1,sP1,aP1,P2,Z1=(as+c)P1)后，判定c是否等于0。为此，模拟器B与敌手A执行以下游戏。

系统建立模拟器B随机选取α,yv,yv′,yq,，并设置参数

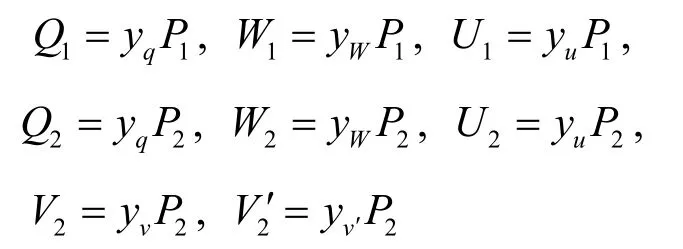
这里相当于隐式地令τ=yv+ayv′，则。接着模拟器B利用α计算其余参数，然后选取2 个哈希函数H0,H1，发送系统公开参数给敌手A

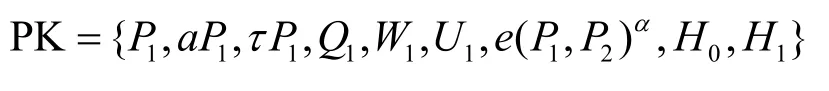
询问由于模拟器B知道系统主密钥，因此能正确回答所有来自敌手A的密钥询问。

伪造当敌手A输出一个关于环Ring 和消息m的伪造环签名后，模拟器B首先计算M=H1(m,Ring)，idi=H0(IDi)（i∈[n]），然后随机选取s′,ctag1,…,，（其中ctagi≠ktagi，i∈[n]），计算T1=s′P1，T2=s′aP1，T3=-s′τP1+s′W,T4,i=s′(idiQ1+ctagiW1+U1)，于是有

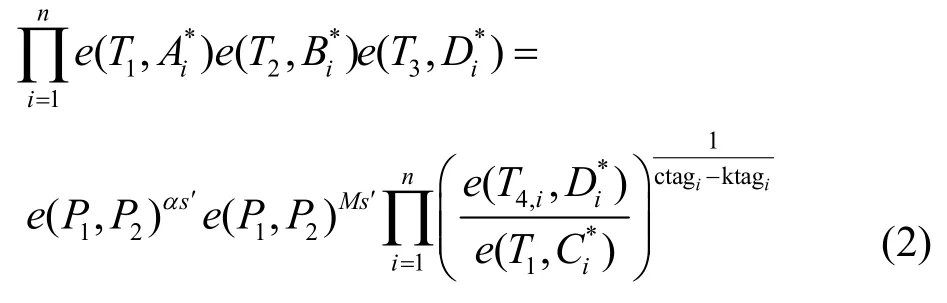
因为敌手A输出的是一个type-S 伪造，所以一定存在π，使。利用这一点，模拟器B便可判定c是否等于0，具体如下。

模拟器B可设置T1=sP1，T2=Z1，+yu)(sP1)，然后验证式(3)是否成立。

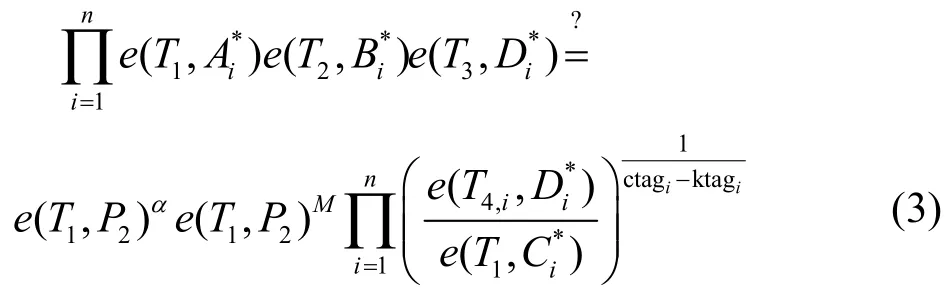
如果c=0，则式(3)成立；否则，式(3)不成立，因为会有额外的一项e(P1,P2)γc≠ 1。

情况2这部分证明中，假设敌手A的伪造为type-N。进一步，假设敌手A共做了L次密钥提取询问和签名询问。该部分证明是通过一系列游戏的game-hopping 技术来完成的，这一系列游戏记为Game0,Game1,…,GameL。

Game0：真实的不可伪造性游戏。

Gamek：对于每个k∈[L]，游戏Gamek如同Game0，除了返回给敌手A的第k个密钥和签名为type-S。

对于每个k∈[L]，Gamek-1与Gamek的不可区分性可归约到DDH2v 困难性假设上。

换句话说，模拟器B的目的是在收到一个DDH2v 实例(P1,dP1,dzP1,zx1P1,P2,dP2,x1P2,x2P2,Z2=(x1x2+c)P2)后，判定c是否等于0。为此，模拟器B与敌手A执行以下游戏。

系统建立模拟器B随机选取a,α,μ,ξ,，并设置参数Q2=-μ(dP2)+yqP2,U2=-ξ(dP2)+yuP2,W2=(dP2)+ywP2,Q1=-μ(dP1)+yqP1,U1=-ξ(dP1)+yuP1,W1=(dP1)+ywP1,V2=-a(x1P2)，

令τ=，则τP1=ayv′P1。同样，Q1,W1,U1也可由dP1类似地计算而得。其余的公开参数以及困难问题中的其他元素均可由a和α计算得到，然后模拟器B选取2 个哈希函数H0,H1，将以下公开参数发送给敌手A

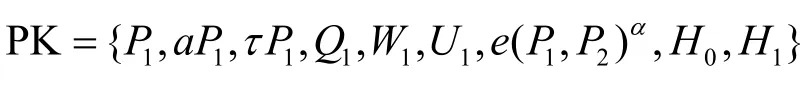
询问对于第j次询问，模拟器B需根据j∈[L]的值给敌手返回type-S 或type-N 的密钥或签名。

如果j＞k，则模拟器B利用主密钥和秘密参数生成一个type-N 的密钥或签名。

如果j＜k且第j次询问是针对身份ID 的一个密钥提取询问，则模拟器B首先生成一个正常密钥然后随机选取计算得到一个半功能密钥

如果j＜k且第j次询问是针对环Ring=和消息m的一个签名询问，则模拟器B首先生成一个正常签名，然后随机选取计算得到一个半功能签名如下。

对于i∈[n]，有以下结论成立。

当i≠π时，有

当i=π时，有

如果j=k且第j次询问是针对身份ID 的一个密钥提取询问，则模拟器B首先生成一个正常密钥，并令ktagID=μid+ξ（其中id=H0(ID)），然后计算身份ID 的私钥

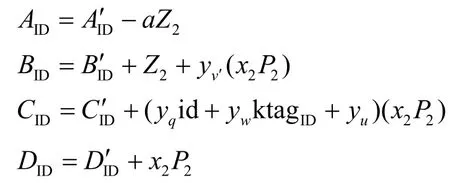
这里隐式地设置r=r′+x2。如果Z2=x1x2P2，则身份ID 的私钥是正常密钥，否则Z2=(x1x2+c)P2，身份ID 的私钥就是一个γ=c的半功能密钥。

如果j=k且第j次询问是针对环Ring={ID1,…,IDn}和消息m的一个签名询问，则模拟器B首先利用主密钥生成一个正常密钥(π∈[n])，选取满足和限制的随机数λi,，选取（其中i∈{1,…,π-1,π+1,…,n}），ktagπ=μidπ+ξ。然后模拟器B回答第j次签名询问如下。

对于i∈[n]，有以下结论成立。

当i≠π时，有

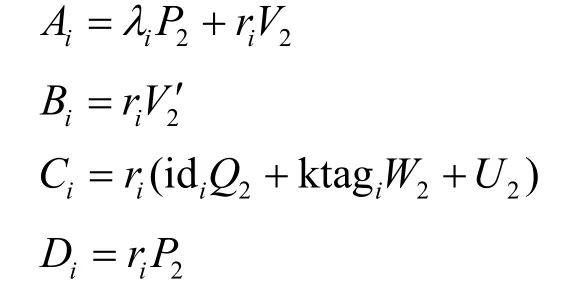
当i=π时，有

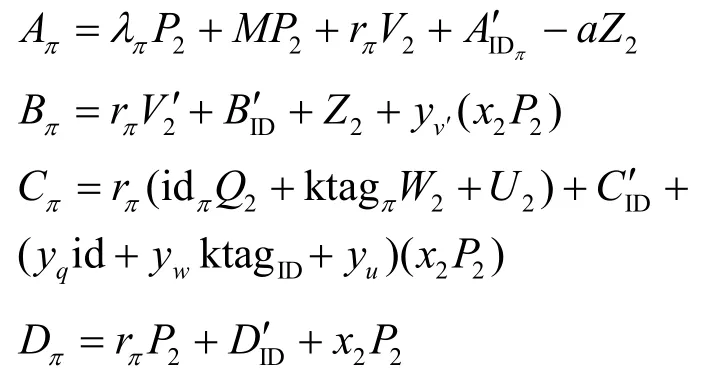
在上述模拟过程中，如果c=0，则模拟器B与敌手A执行游戏Gamek-1；否则，执行游戏Gamek。如果敌手A在这2 个游戏中获胜的概率有差异，则模拟器B利用这点差异就可以解决DDH2v 问题。然而，如果敌手A的伪造由type-N转变为type-S，A在这2 个游戏中获胜的概率有可能保持不变。因此，模拟器B不得不检测A输出的伪造是否仍然是type-N。为此，B随机选取，对于每一个i∈[n]，设置ctagi=μidi+ξ，并计算

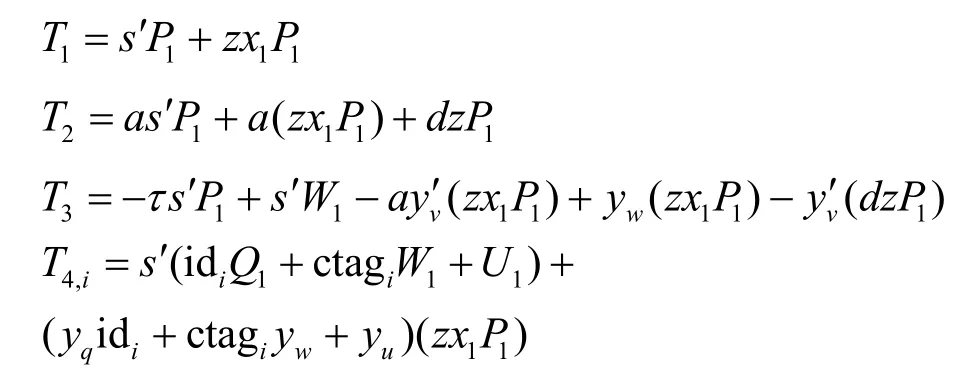
这里隐式地设置s=s′+zx1。然后B验证式(5)是否成立。

如果伪造为type-N，则式(5)成立；否则，式(5)不成立，因为会产生额外的一项e(P1,P2)dzγ。

因此，如果敌手A能够区分Gamek-1和Gamek，模拟器B就能利用敌手A的能力攻破DDH2v 假设。

最后，本文证明如果敌手A在游戏GameL中输出一个type-N 的伪造，模拟器B就能利用敌手A的能力攻破DBDH 假设。

这里需要注意的是，由于B并不知道α，因此仅能生成半功能密钥给A。

签名询问为了回答签名询问，模拟器B首先利用米主要生成签名者IDπ的一个半功能密钥，选取满足和限制的随机数λi,ri,，然后回答签名询问如下。

对于i∈[n]，有以下结论成立。

当i≠π时，有

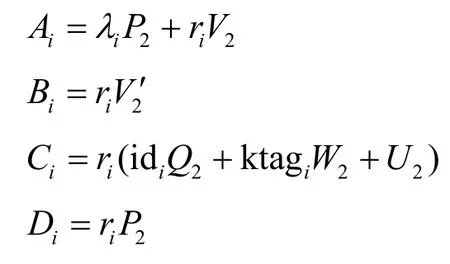
当i=π时，有

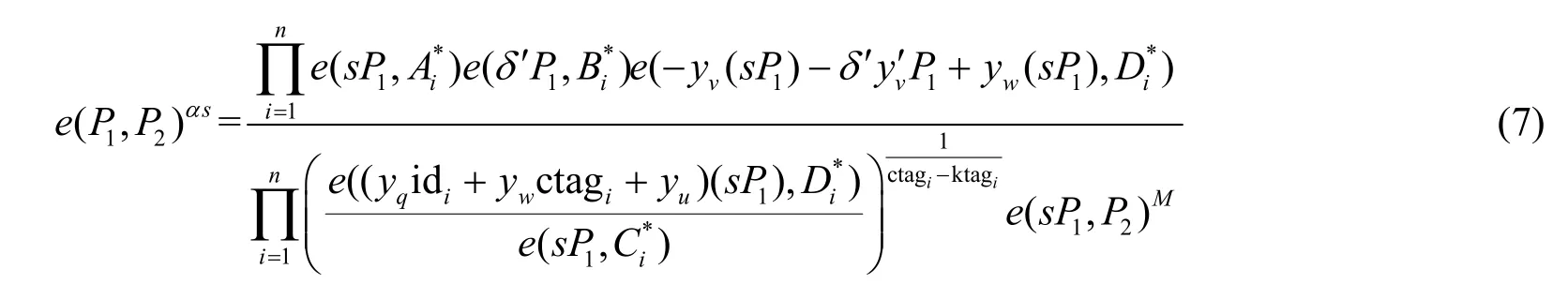
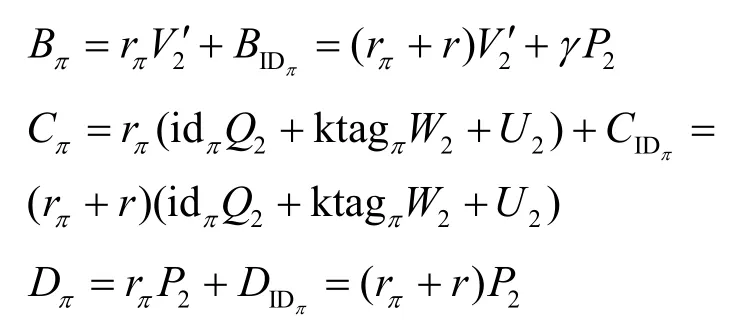
最终得到一个type-S 的签名。

这里，模拟器B隐式地设置δ′=δ+as，其中。然后B通过检验e(P1,P2)αs=Z3是否成立攻破DBDH 假设。

定理2匿名性。3.1 节给出的环签名方案是无条件匿名的。

证明签名中，由于是由真实签名者随机生成的，因此{Ai,Bi,Ci,Di,ktagi}(i∈[n]{π])是均匀分布的。另一方面，由于αP2是主密钥，r和ktagπ是由PKG随机生成的，与真实签名者无关，因此{Aπ,Bπ,Cπ,Dπ,ktagπ]也是均匀分布的。因此，整个签名过程中，有关真实签名者的信息没有被泄露。敌手想要通过签名确定真实签名者身份的概率不会优于从环Ring={ID1,…,IDn}中随机猜测真实签名者身份的概率。故3.1 节给出的环签名方案是无条件匿名的。

5 性能比较

本节将本文方案与已有的基于对偶系统的身份基环签名方案[22-23]进行性能比较。

为了比较方案在各个阶段的运行效率，本文使用Java 语言编程实现3 个方案，通过调用JPBC 密码库实现相关的密码运算，基于PC 端开发，主要运行环境如下。中央处理器：AMD Ryzen 7-4800H；内存：16 GB；硬盘：240 GB；操作系统：Windows 10 专业版。

图1～图4 是本文方案与文献[22-23]中各算法运行时间的对比曲线。由图1～图4 可以看出，由于本文方案在素数阶群上构造，因此在效率方面具有很大优势。

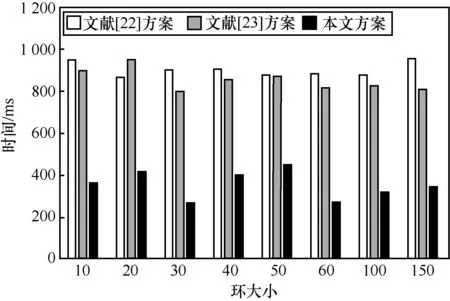
图1 各方案Setup 算法的性能比较

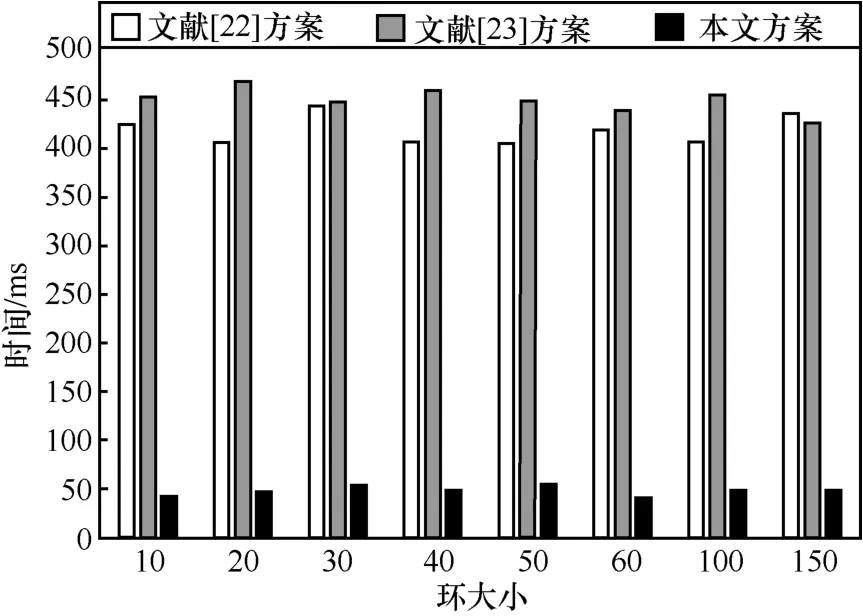
图2 各方案Extract 算法的性能比较

图3 各方案Sign 算法的性能比较

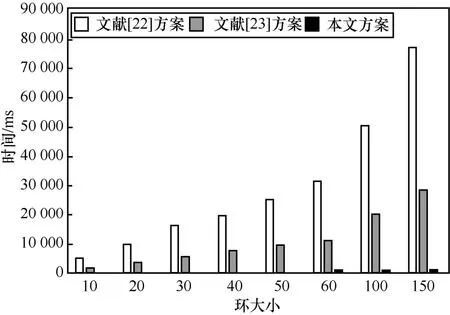
图4 各方案Verify 算法的性能比较

表1 列出了当环大小为n=150时3 个方案中各个算法的操作时间，相较于文献[22-23]方案，本文方案中各算法运行时间更短，这主要是因为文献[22-23]方案是基于合数阶群上的对称对构造的，而本文方案是基于素数阶群上的非对称对构造的。对运算是各个算法中最耗时的运算，而合数阶群上的对运算要比素数阶群上的对运算慢许多。相比于对称对，非对称对在实现时也更快更紧致。

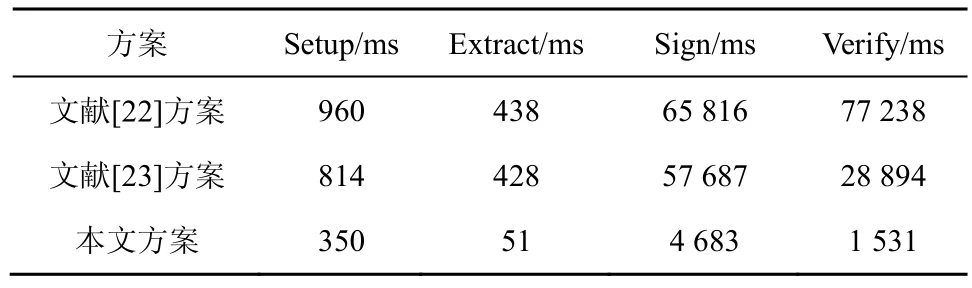
表1 环大小为n=150 时的计算效率比较

6 结束语

环签名中，环中任意成员都能以一种完全匿名的方式对消息进行签名。这一性质被称为环签名的无条件匿名性，可用于保护签名者的隐私。因在隐私保护等方面的重要应用，身份基环签名已成为一个热门的研究方向。然而，大多数已有的身份基环签名方案的安全性证明不是基于随机预言机模型就是使用了公共参考串模型。本文提出了一个基于素数阶群上非对称对的身份基环签名方案。基于对偶系统加密技术，该方案被证明在标准模型下是不可伪造和无条件匿名的。与文献[22-23]方案相比，本文方案更高效。然而，本文方案中签名大小仍然会随着环成员个数的增长而呈线性增长。因此，在素数阶群上基于对偶系统加密技术构造标准模型下，可证明安全的具有常量大小的身份基环签名方案是笔者今后研究的主要方向。