基于自适应神经模糊推理系统的导弹直/气复合控制系统设计

邓伟伟，段朝阳，闫 亮

(中国空空导弹研究院，洛阳 471009)

0 引言

随着武器技术的进步和装备的发展，现代战争中以第四代战斗机及高超声速巡航导弹为代表的高空、高速、高机动目标不断涌现，对导弹的敏捷转弯能力和末端精确打击能力提出了更高的要求，导弹面临严峻挑战。为了弥补传统气动舵控制的不足，采用直/气复合控制来提高导弹的响应特性，实现对目标的精确打击。

针对导弹直/气复合控制问题，国内外学者已经开展了大量研究工作[1-4]，导弹直/气复合控制系统是一个非线性、时变、多变量复杂控制系统，难以建立精确的数学模型，基于经典与现代控制理论设计的导弹直/气复合控制系统依赖精确的数学模型，缺乏自学习和自适应能力。近年来，人工智能成为研究热点，未来是智能化战争时代，各国为占领智能化军事领域制高点，都在加快研究智能武器装备[5]，导弹直/气复合控制系统智能控制也得到了相应的研究。神经网络[6]、模糊控制[7-8]和遗传算法[9]结合了定性决策和定量控制，将人的经验与思维加入到导弹直/气复合控制系统中，设计过程不依赖精确的数学模型，但是各类智能控制存在着不可避免的缺点。模糊控制表达人脑的推理能力，设计相当依赖专家或操作人员的经验与知识，若缺乏这样的经验，很难获得满意的控制效果。神经网络模拟人脑的组织结构，具有自学习能力，但实际类似于一个黑箱，缺少透明度，可解释性较差，不能很好地表达人脑的推理功能。自适应神经模糊推理系统(Adaptive Neural-based Fuzzy Inference System，ANFIS)将二者有机地结合起来，通过神经网络建立具有自学习能力的模糊控制系统，利用神经网络的学习机制补偿模糊控制系统原有的缺点，能够得出比较科学合理的参数，从而提高整个系统对知识的学习和表达能力。

本文以末制导段空空导弹为研究对象，建立俯仰通道数学模型，设计2输入2输出的模糊控制器。采用自适应神经模糊推理系统，通过样本数据学习，优化常规模糊控制。直接力装置数学模型首先采用线性化模型进行设计，之后通过脉冲调宽调频(Pulse Width Pulse Frequency，PWPF)调制器对线性化设计得到的直接力控制量进行调制，得到离散的开关指令。仿真结果表明，基于ANFIS的导弹直/气复合控制系统能够快速精确地跟踪导弹加速度指令，提高系统的控制品质。

1 直/气复合导弹数学模型

1.1 导弹动力学模型

空空导弹直/气复合控制采用姿控式，直接力装置位于质心后，结构如图1所示。

导弹俯仰通道上小扰动线性化动力学方程[10]为

(1)

俯仰通道状态空间模型为

(2)

其中

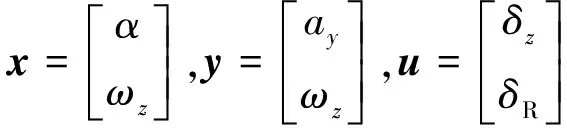
1.2 执行机构数学模型

气动舵数学模型描述为如下二阶系统

(3)

直接力装置数学模型描述为如下一阶系统

(4)

2 导弹直/气复合控制系统设计

2.1 模糊控制原理

模糊控制是一种简单地将某一空间的输入映射到另一空间的输出的规则[11]。模糊控制的人机对话能力强，方便将人的思考逻辑加入控制过程。模糊控制分为模糊化、模糊推理和解模糊3个过程，3个过程的完成基于知识库。

知识库包含了应用知识以及控制目标，由数据库和规则库构成。数据库包括隶属函数和尺度变化因子等，规则库包括模糊语言构成的一系列控制规则。模糊化是将输入指令的清晰量转化为模糊量，以便于模糊推理。模糊推理是模糊控制的核心，基于模糊概念模拟人的推理能力，一般基于控制工程知识、操作人员实际操作过程等来模仿人的决策行为，通过相应的模糊控制规则，得到控制指令的模糊量。解模糊是将模糊推理得到的控制指令的模糊量转化为实际控制的清晰量。模糊控制器结构如图2所示。

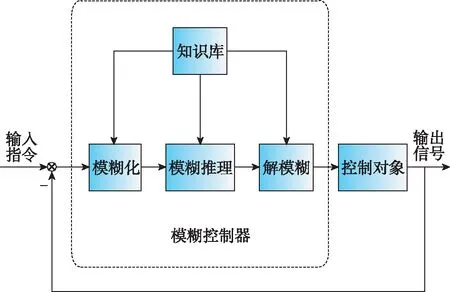
图2 模糊控制器结构

2.2 自适应神经模糊推理系统原理

自适应神经模糊推理系统利用神经网络的学习能力，通过对样本数据的学习实现模糊控制的模糊化、模糊推理和解模糊3个过程，优化模糊控制的知识库，建立具有自学习、自适应能力的模糊控制系统[12]。以2输入(x1,x2)和1输出(y)的系统为例，模糊if-then规则如下：

规则1：ifx1isA1andx2isB1thenf1=p1x1+q1x2+r1

规则2：ifx1isA2andx2isB2thenf2=p2x1+q2x2+r2

自适应神经模糊推理系统可以认为是T-S型模糊控制的神经网络实现，该网络是一个多层前馈网络，结构如图3所示。

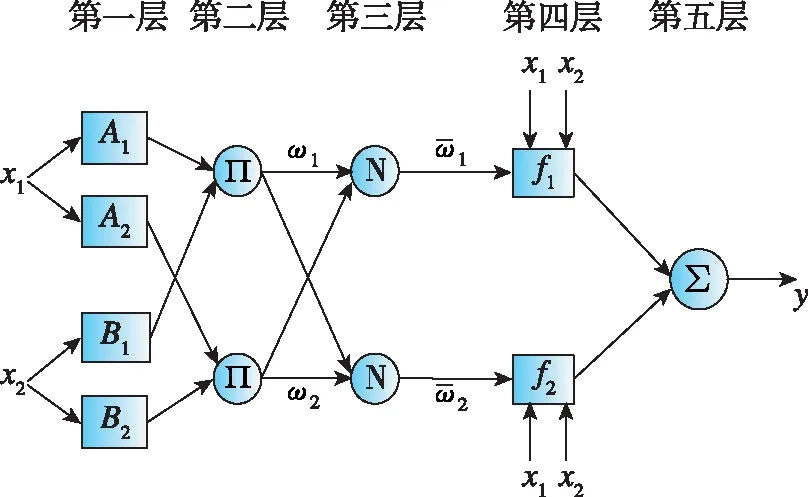
图3 自适应神经模糊推理系统结构

第一层：输入变量模糊化，该层参数可变，每个节点是以节点函数表示的方形节点

O1,i=μAi(x1),i=1,2;O1,i=μB(i-2)(x2),i=3,4

(5)

其中，x1(或x2)为节点的输入；O1,i为模糊集Ai(或Bi-2)的隶属函数，隶属函数的参数集为前提参数。

第二层：模糊集运算，输入信号相乘，而将其乘积输出为

O2,i=ωi=μAi(x1)μBi(x2),i=1,2

(6)

第三层：计算每条规则ωi与全部规则ω之和的比值为

(7)

第四层：计算每条规则输出为

(8)

其中，{pi,qi,ri},i=1,2为结论参数。

第五层：计算所有输入信号的总输出为

(9)

自适应神经模糊推理系统根据样本数据学习调整前提参数和结论参数，对于集上任意函数有无限的逼近能力，为复杂系统的控制提供了有效的工具。

2.3 PWPF调制器

PWPF调制器由一阶惯性环节、施密特触发器以及反馈回路组成，如图4所示。

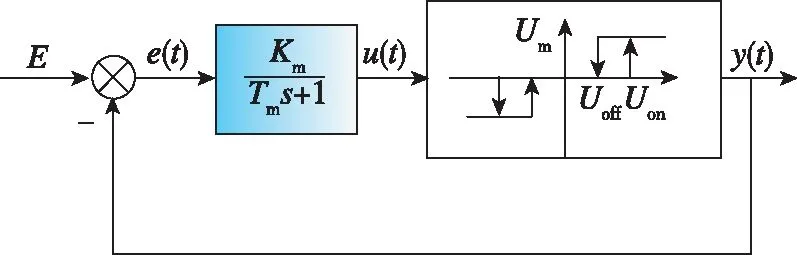
图4 PWPF调制器

其中，Km为一阶惯性环节放大系数，Tm为一阶惯性环节时间常数；Uon和Uoff为施密特触发器的开关阈值，Um为施密特触发器的脉冲幅值。脉冲调制基于冲量等价原理，采用PWPF调制器可以将连续推力转化为等效的常值脉冲推力。

2.4 导弹直/气复合模糊控制系统设计

结合纯气动舵控制采用的经典Raytheon三回路结构[13]，针对导弹直/气复合控制数学模型，直接力控制回路与气动舵控制回路并行工作，建立导弹直/气复合模糊控制系统，如图5所示。

图5 导弹直/气复合模糊控制系统

加速度误差信号ea和角速度误差信号eω为模糊控制器的输入;气动舵控制信号δz和直接力控制信号δR为模糊控制器的输出;弹体加速度ay和俯仰角速度ωz为反馈信号。

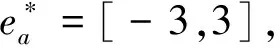
自适应神经模糊推理系统的输入为加速度误差与角速度误差，输出为直接力控制与气动舵控制。采用离线学习模式，通过线性二次型调节器(Linear Quadratic Regulator, LQR)采集样本数据,分为训练、测试、检核3个部分，对于装入系统的样本数据通过网格分割法，按照设定参数，依据模糊C-均值聚类方法建立模糊推理系统。依据模糊控制的设计经验，设置模糊子集个数为7，选取三角形隶属函数，输出为线性函数。利用混合最小二乘估计的反向传播算法,确定自适应神经模糊推理系统的前提参数和结论参数，确定与输入输出样本数据相匹配的模糊控制知识库，建立具有自适应能力的模糊推理系统。

3 仿真验证及结果分析

选取导弹在高度12km，马赫数3.0的特征点进行设计，其状态方程矩阵为

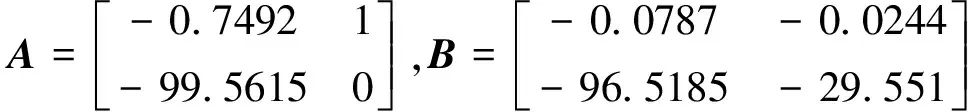
执行机构参数ωδ=120，ξ=0.7，τ=0.02；稳态传递增益Kωss=0.00113；PWPF调制器参数选取为Km=5，Tm=0.1。

图6～图10所示为加速度10m/s2的仿真结果。可以看出，常规模糊控制相对于LQR超调量更小，控制用量更优，控制品质更高。当加速度指令变化时，基于经验设计的常规模糊控制的知识库需要更新，经验不足时一般采用试凑法完成知识库更新，设计过程复杂。图11～图14所示为加速度100m/s2的仿真结果。可以看出，自适应神经模糊推理系统控制品质优于常规模糊控制，常规模糊控制设计由于经验不足，加速度指令跟踪存在一定的稳态误差与振荡。图15～图17所示为直接力装置采用PWPF调制器，验证导弹直/气复合控制系统的离散特性。加速度响应曲线上升段的波动是由于直接力装置点火产生的瞬时推力造成的正常现象。仿真结果表明，基于ANFIS的导弹直/气复合控制系统能够快速精确地跟踪导弹加速度指令。

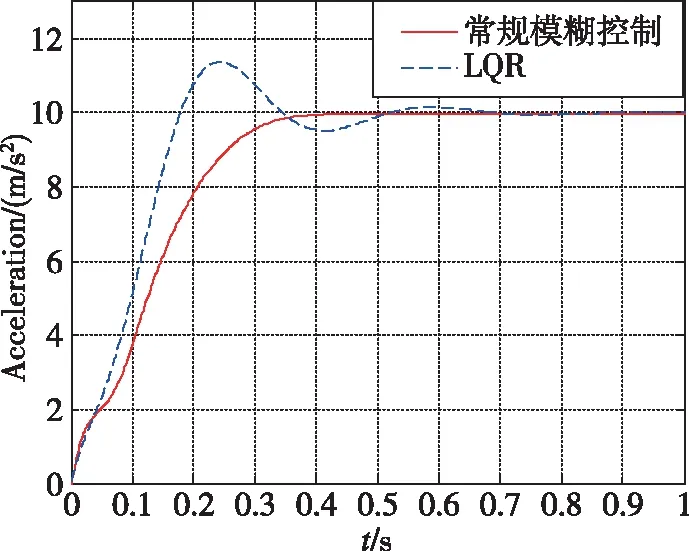
图6 加速度指令10m/s2时加速度响应

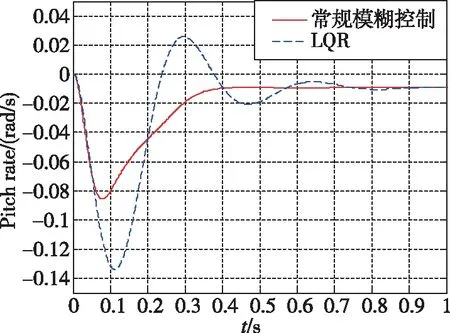
图7 加速度指令10m/s2时俯仰角速度响应

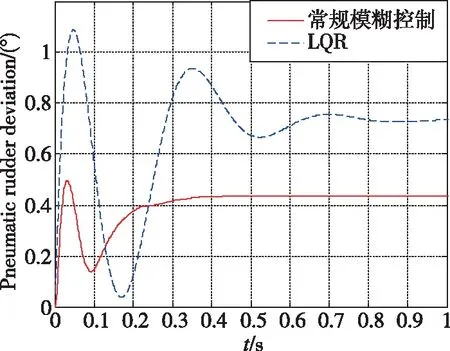
图8 加速度指令10m/s2时气动舵偏用量

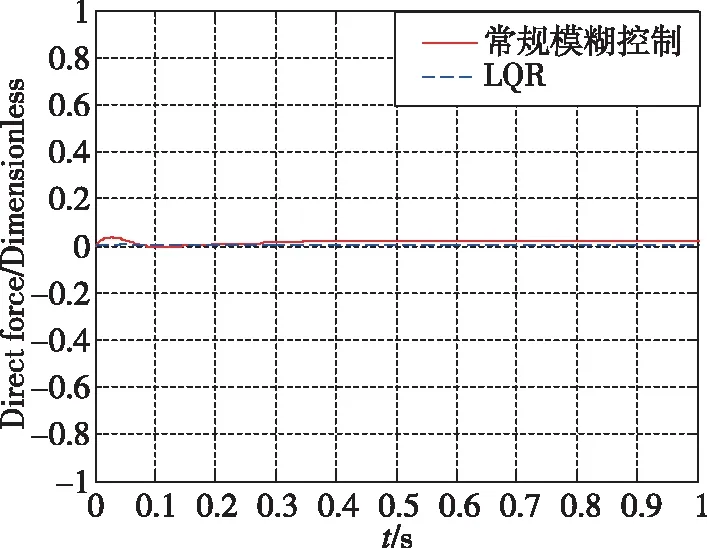
图9 加速度指令10m/s2时直接力用量

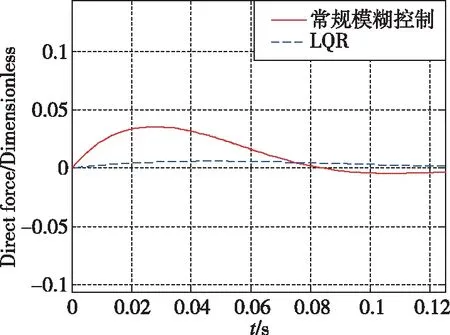
图10 直接力用量局部放大

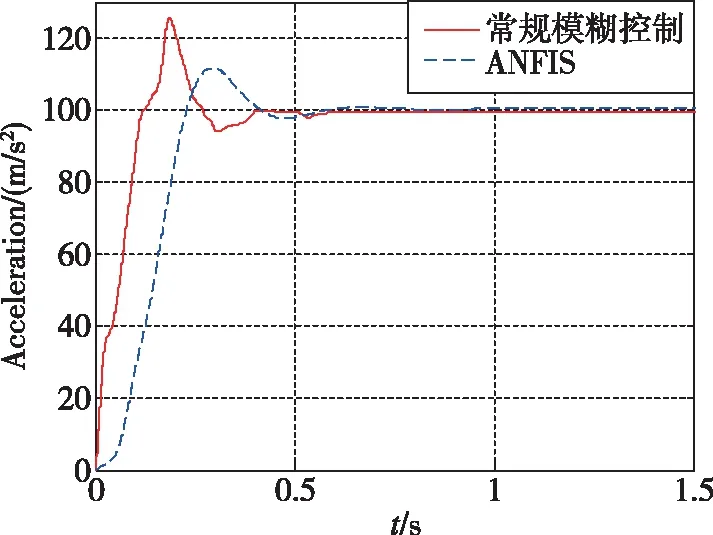
图11 加速度指令100m/s2时加速度响应

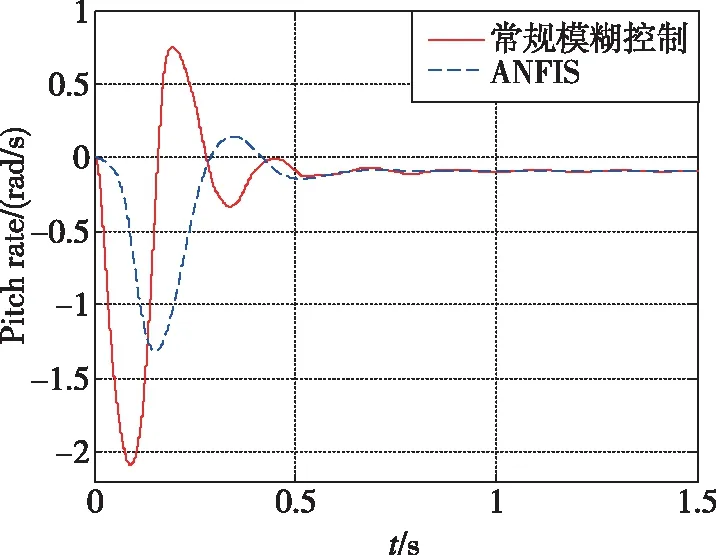
图12 加速度指令100m/s2时俯仰角速度响应

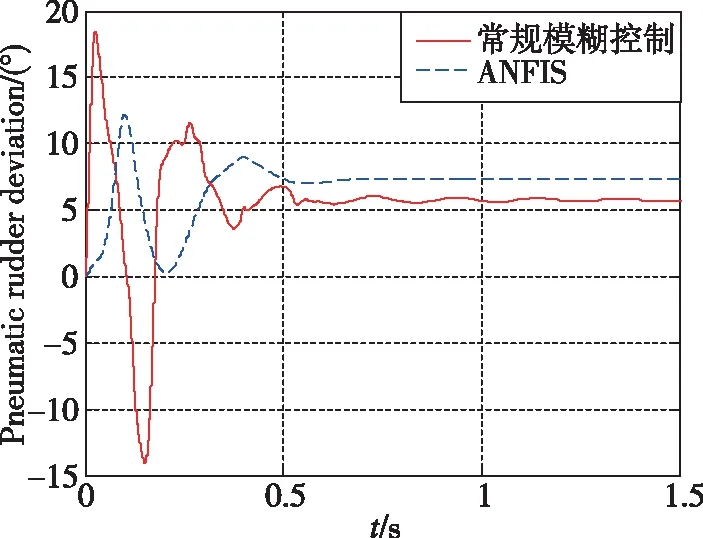
图13 加速度指令100m/s2时气动舵偏用量

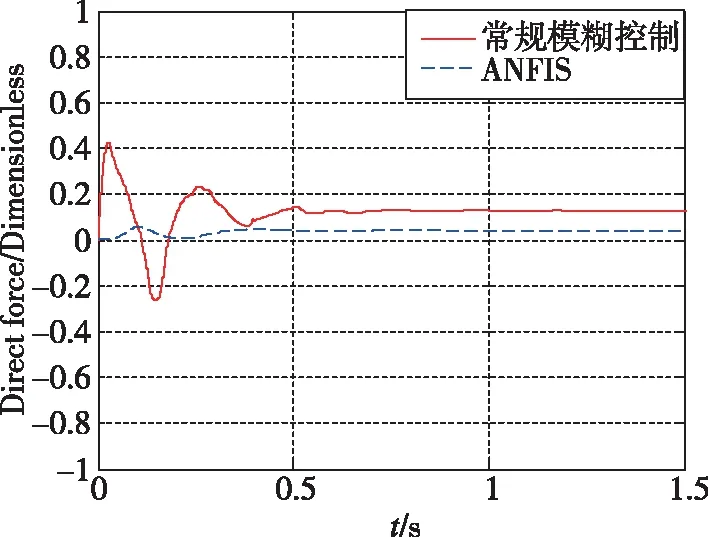
图14 加速度指令100m/s2时直接力用量

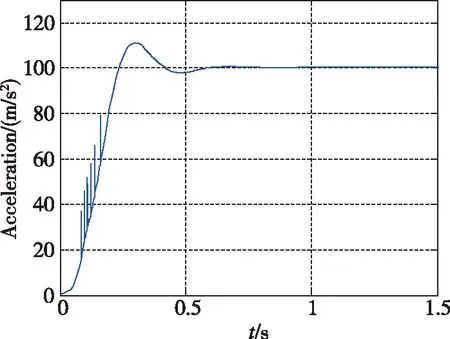
图15 采用PWPF调制器的加速度响应

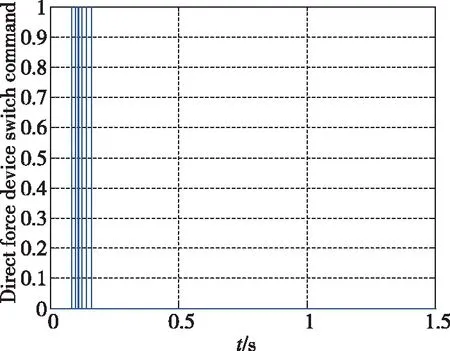
图16 采用PWPF调制器的直接力装置开关指令

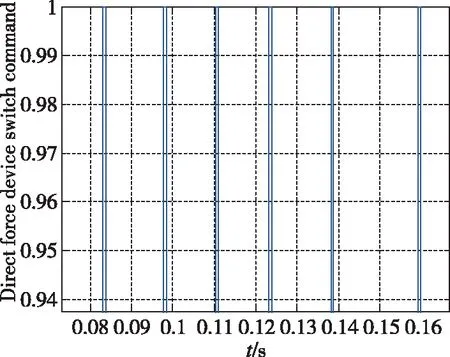
图17 直接力装置开关指令局部放大

4 结论

本文针对空空导弹直/气复合控制问题，基于ANFIS设计了导弹直/气复合控制系统。常规模糊控制设计基于经验，不依赖精确的数学模型，但是当系统工作状态变化时，知识库相应地需要更新，设计过程复杂，经验不足时难以保证控制品质。本文通过引入神经网络，建立了自适应神经模糊推理系统，通过样本数据学习建立了模糊控制知识库，优化了常规模糊控制。采用PWPF调制器对线性化设计得到的直接力控制量进行调制，得到离散的开关指令，验证了导弹直/气复合控制系统的离散特性。仿真结果表明，常规模糊控制的控制品质优于LQR，系统状态发生变化时，基于ANFIS的导弹直/气复合控制系统可以实现加速度指令的快速精确跟踪，改善了空空导弹的响应特性。