基于图神经网络的医疗物资智能调度研究优化
黄承宁,李 娟,陈嘉政
(南京工业大学浦江学院,江苏 南京 211222)
0 引 言
随着电子商务兴起,物资调度系统应用已经深入到人们的生活学习之中,如何让调度与物资路线更加智能化、配送成本与效率反相关等已经成为更多研究人员的课题。传统广泛应用的是蚁群算法为基础的路径构建[1],但是随着物资处理数量剧增,逐渐显现出计算复杂度高、收敛速度慢、全局最优缺失等问题。在这种情况下准确的医疗物资运输和病患分流状况实时预测对于医疗工作者,确诊患者和疑似病患,以及企业部门和政府而言至关重要。
随着移动物联时代的到来,各类数据呈爆炸式增长,对于大数据的研究已渗透到人们生活的各个方面。机器学习、深度学习等算法的提出让研究人员得以充分发挥数据的规模效应。获取到的大规模的数据在一定程度上把研究人员从愈加复杂的数学模型中解放出来,使得他们专注于数据本身,大大提高了系统的适用性、可靠性以及鲁棒性[2-3]。机器学习、深度学习等前沿技术在图像、语音、文字处理等方向的成功应用也给物资调度系统的优化带来了新的思路。以机器学习算法为基础,以影响资源调度的各因素作为输入,以成本节约最优、配送效率最快的配送方案及路线作为输出,进行训练、学习,得到一种精度高、可靠性高、鲁棒性高的物资智能调度算法。
在交通研究中,交通流量的基本变量即通常选择速度、体积和密度作为指标,监控交通状况的当前状态以及预测未来。根据预测的时长,流量预测通常分为两个等级,即短期和中长期。最普遍统计方法(例如,线性回归)能够在短期预测中表现良好。但是,由于对于交通流量的不确定性和复杂性,这些方法对于相对长期的预测而言效果较差。以前关于中长期流量预测的研究可以大致分为两类:动态建模和数据驱动的方法[4]。动态建模用数学工具和物理通过计算来解决交通问题的数学建模。为了达到稳定状态,模拟过程不仅需要复杂的系统编程,也消耗了大量计算功率。不切实际的假设和简化建模也会降低预测准确性。因此,随着交通数据收集和存储技术的快速发展,许多研究人员正在将他们的注意力转到数据驱动的方法上。
通过为每个医疗点运输路线建模,并记录每个节点与其可能存在交互车辆之间的边缘,从而获得交通场景的稀疏点阵,存储为一个图特征。同时,已显示该机器学习模型,尤其是深度神经网络在这个问题上表现良好。然而学习模型对固定大小的数据进行操作并具有固定的空间组织,例如单个数据点,时间序列或图像输入。直到最近才出现图神经网络(GNN),即人工深度神经网络在图数据上运行的计算图模型,并享有显著成功。这大大改善了可扩展性,同时提高了性能。
GNN在对图形中节点间的依赖关系进行建模方面能力强大,使得图分析相关的研究领域取得了突破性进展。但由于图结构数据的表示一般是不规则的,传统的GNN等模型无法直接运用在图数据上,所以需要在图上重新定义卷积操作,因此,在捕获结构化依赖上扮演着中心角色的图卷积网络GCN应运而生[5-7](见图1)。
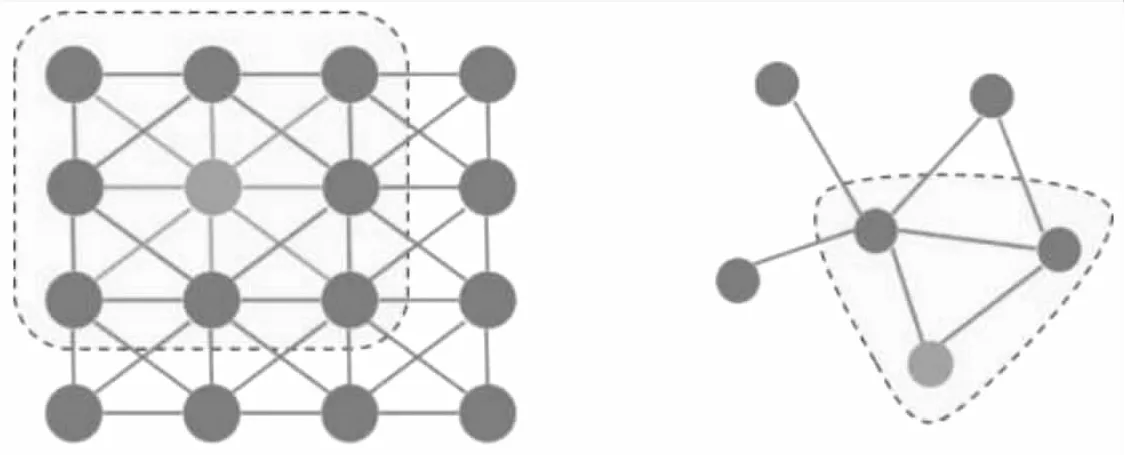
图1 从GNN到GCN
1 基于深度学习的搜索算法
在智慧医疗建设中,除了医学和生物学研究外,理论研究以及基于统计或数学建模的实体也可能发挥不可忽略的作用。对于了解疫情的流行特征,预测疫情并确定遏制蔓延的措施。物资调度路径非常适合用图数据来表达,如调度路径网络中的节点以及节点与节点之间的关系。对于图数据既要考虑节点信息,也要考虑结构信息,而图卷积神经网络正好可以自动化地既学习节点特征,又能学习节点与节点之间的关联信息。因此图神经网络模型对于优化控制交通运输有着巨大的作用。
1.1 医疗调度运输流量预测
根据Lef‘evre等人的调查,将车辆行为预测模型分为基于物理、基于机动和交互觉察三种模型[8]。
基于物理的模型通常假设车辆没有动作,而是使用恒定速度或加速度,然后仅根据物理模型预测运动。这些模型可以用于跟踪[9],但通常智能预测瞬时运动状态。
基于机动的模型使用一组机动原型并使用基于聚类的聚类直接匹配过去的轨迹方法或使用机器从车辆特征学习方法[10]。这些做法可以进行更复杂的机动,但无法考虑互动。
交互意识模型旨在根据已有车辆的状态进而预测车辆输出模型。这些预测模型包括扩展冲突的基于机动的模型、耦合隐马尔可夫模型(HMM)以及对实体依赖或基于机器学习的模型等[11]。根据基于机器学习模型的复杂度不同,可以使用简单的前馈神经网络创建用于蒙特卡洛的快速模型树搜索算法。也可以使用用于相同任务的循环神经网络(RNN),或使用生成对抗式模仿学习从而强化学习驾驶行为。
1.2 卷积图神经网络
图像上的卷积规则网格的标准卷积显然不适用于一般拓扑图。GCN的本质目的就是用来提取拓扑图的空间特征。当前有两种基本方法探索如何将CNN概括为结构化数据形式。一种是扩展卷积的空间定义[12],另一种是在图傅里叶变换的光谱域[13]。前一种方法将顶点重新排列为可以通过常规卷积处理的某些网格形式操作,即空域可以类比到直接在图片的像素点上进行卷积。后者介绍光谱通常在频谱域中应用卷积的框架称为频谱图卷积[14],即频域可以类比到对图片进行傅里叶变换后再进行卷积。几次改进研究使图卷积更具前景,将计算复杂度从O(n2)降低到线性相关。
图卷积神经网络实际上跟CNN的作用一样,就是一个特征提取器,只不过它的对象是图数据。在GCN中,精妙地设计了一种从图数据中提取特征的方法,从而可以使用这些特征对图数据进行节点分类(node classification)、图分类(graph classification)、边预测(link prediction),还可以得到图的嵌入表示(graph embedding)[15]。GCN的核心部分就是可以很好地提取图数据结构的特征,通过kernel小窗口在图片上平移,通过卷积的方式来提取特征,且图片结构具有平移不变性:一个小窗口无论移动到图片的哪一个位置,其内部的结构都是一模一样的,可以实现参数共享。
卷积提取特征过程如图2所示。
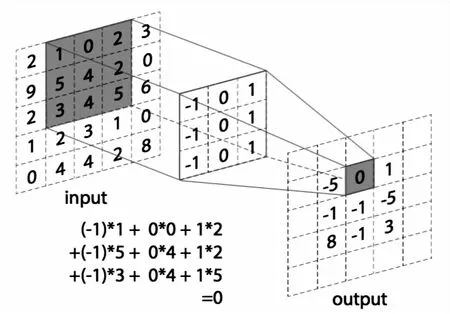
图2 卷积提取特征过程
上文介绍了图卷积神经的概念,假设基于频谱图卷积信号为G,则G为信号维度x2Rn与核的乘积,如公式(1)所示。
Gx=(L)x=(UUT)x=U*UTx
(1)
而其中傅里叶变换D∈Rn×n是归一化拉普拉斯算子的特征向量。
(2)
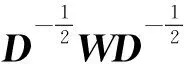
通过使用上述算法,可以把交通运输情况转化为大规模图数据进行运算,作为疫情期间交通运输的优化策略。
2 算法优化实现
GCN是一种基于节点的图分类或预测的方法。类似于图像或时间序列上的卷积,GCN在所有节点上应用相同的操作。像其他神经网络一样,它由一系列相继应用的不同参数层定义。假设有一批图数据,其中有N个节点(node),每个节点都有自己的特征,设这些节点的特征组成一个N×D维的矩阵X,然后各个节点之间的关系也会形成一个N×N的矩阵A,称为邻接矩阵(adjacency matrix)。X和A便是模型的输入。
在数据输入到输入层之前要先对数据进行预处理,卷积神经网络的输入数据需要进行标准化处理才可以使用,若输入值为像素而像素的大小范围是在[0,255]之内,则卷积神经网络的输入值是通过归一化取得的像素值与255的比值,将数据归一化在[0,1]的区间范围内。卷积层的功能是对输入到卷积神经网络的数据进行深入的分析得到数据的最具有代表性的特征。卷积层是通过卷积核来实现卷积的。卷积层的主要特征在于卷积核、卷积层参数和激励函数。卷积神经网络的输出层的上一层一般是全连接层,把所有的特征都作用在神经元上,连接所有学习到的特征将输出值送给分类器,一般选择Softmax分类器,最终输出分类标签。
2.1 基本模型
GCN也是一种神经网络,每一层都使用卷积机制,层与层之间的传播方式如公式(3):
(3)
其中,H是每一层的特征,对于输入层的话,H就是X,H(l+1)是第l层的激活,σ是非线性激活函数,A是在节点之间添加了自连接的邻接矩阵,D是度向量A中的一个,而W(l)是第l层可学习的权重矩阵。
通过公式(3),不仅可以很好地提取图的特征,且若向GCN输入一个图,通过若干层GCN每个node的特征从X变成了Z,无论中间有多少层,node之间的连接关系,即A,都是共享的,很好地实现了层特征传播。具体图神经卷积[16-17]如图3所示。
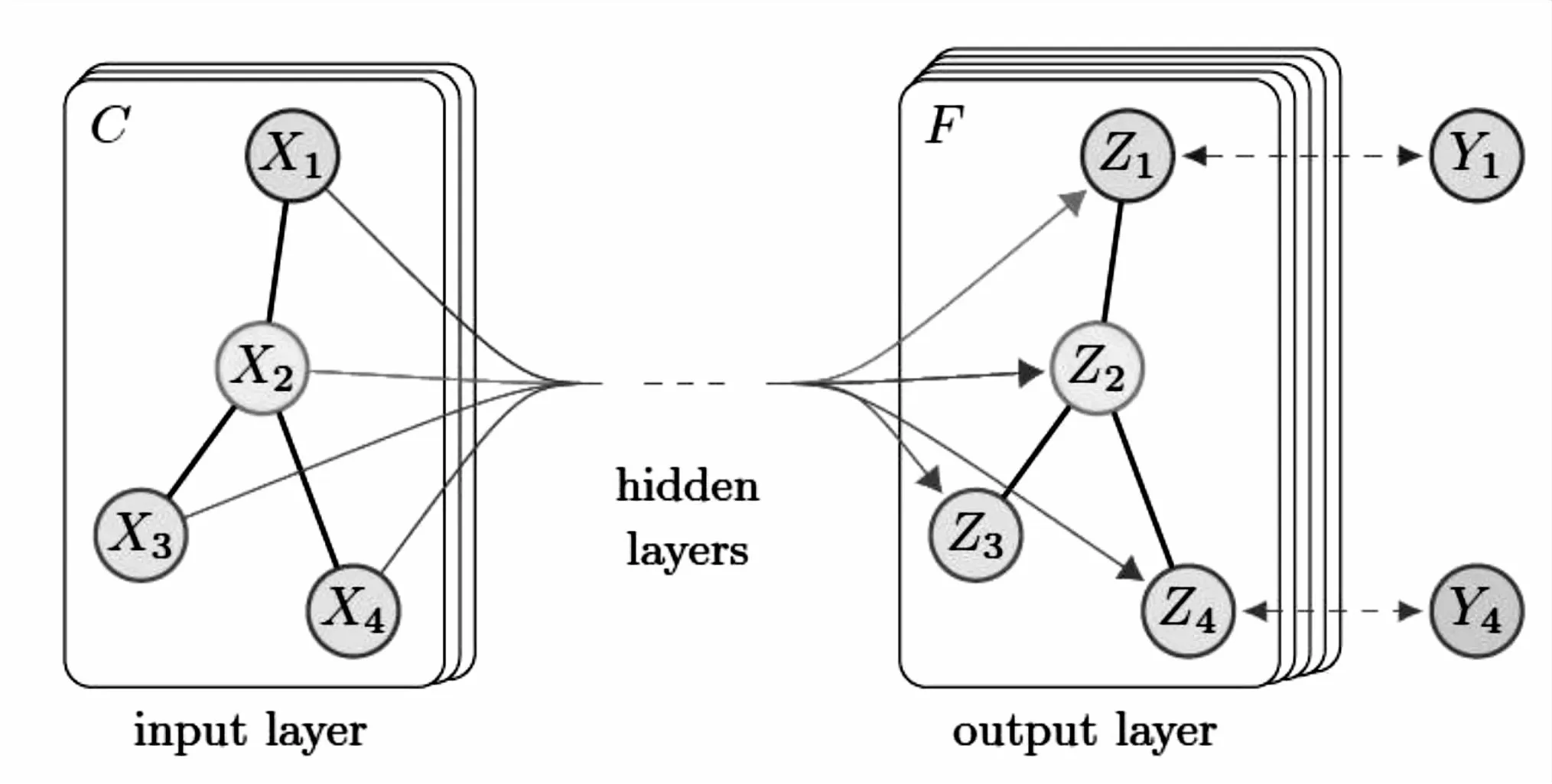
图3 图神经卷积
这等效于局部频谱滤波器的一阶逼近,但具有两个关键优势:图拉普拉斯算子不需要反转,这将导致更高的计算成本,并且指定了转换l层的大小恰好将节点的l度邻域考虑在内。因此,计算复杂度在边缘的数量上线性地缩放,并且可以考虑未直接连接到自我车辆的车辆。这使其比相邻车辆的直接编码更有效。
2.2 对GCN的优化
为了探索图拉普拉斯矩阵为指明的隐藏结构,文献[18]提出了自适应图卷积网络(AGCN)。AGCN利用所谓的残差图来扩充图,残差图是通过计算节点对的距离来构造的。尽管AGCN能够捕获互补关系信息,但是以O(N2)的计算量为代价。AGCN通过图的邻接矩阵学习未知的隐藏结构关系。它通过一个以两个节点的特征为输入的可学习的距离函数来构造一个所谓的残差图邻接矩阵。
在优化过程中主要实现的目标:(1)加快算法收敛速度;(2)尽量避过或冲过局部极值;(3)减小手工参数的设置难度,主要是Learning Rate(LR)。梯度下降是最流行的优化算法之一,并且目前为止是优化神经网络最常见的算法。目前每种深度学习库都包含各自优化实现的梯度下降算法,常见的有Adagrad 、Adadelta、Adam等。在实验中,每种优化算法针对具体需求各有其优缺点,通过对优化过程中鞍点处理对比来看,效果如图4所示。
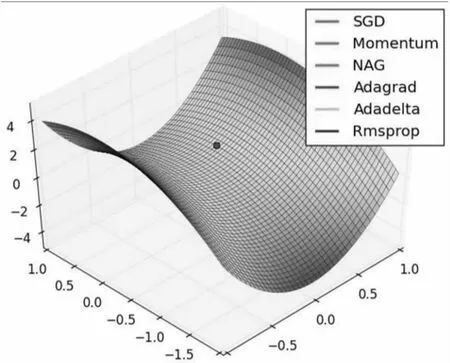
图4 鞍点处优化算法比较
对于GCN,除了提出自适应图卷积网络优化改进,还存在一些改进,但是目前GCN的分类准确率仅为80%左右,即使增加GCN层数,准确率也不一定提高。同时GCN容易受到图结构的干扰,这些图是随机的或经过对抗性设计的。扰动的连接性会破坏图结构,从而严重影响GCN在半监督学习(SSL)任务中的性能。针对交通中的动图对GCN健壮性减弱的问题,实验改进过程中生成了多个辅助图,每个辅助图随机地增加或者删去一些邻变。配置使用自适应(A)GCN在生成辅助图进行半监督的学习。通过合适的正则化方法,学习到辅助图融合的权重,可以实现保障GCN的健壮性。相对于GCN,新型AGCN在噪声输入,结构微小扰动和最先进的对抗性攻击测试中均获得了显著改善的性能。
在基本GCN的应用实现过程中,做了重要改变与设置:其中一项就是剩余权重,GCN根据该节点邻域的频谱分解以及添加的自连接,即节点本身来计算该节点的下一层功能。但是,这意味着GCN不能将节点的自身特征与其邻居节点区别对待。在预测任务中,这似乎是良好性能的重要障碍。因此,删除了自连接,同时引入了第二个权重矩阵,该矩阵定义了自节点特征的转换。变换方程如公式(4)所示。
按距离的权重,是指邻接矩阵可以是二进制的也可以是加权的,通过反距离评估加权边,自环设为1。
前馈输出,实验中不再使用完整的GCN,而是将输出层替换为对每个节点的功能独立运行的前馈层,如此可以更好地解耦特征提取(发生在前几个GCN层中)和根据提取的特征进行预测,且GCN层数不宜多,2~3层(多了容易产生过平滑现象,同时加深网络会导致模型的效果变差)的效果最佳。
鉴于网络的输入数据存在调整需求,此时其数据位节点度、节点信息,节点K接邻居信息的concat结果,仅为通过在输入数据中加入度信息和邻居信息,此情境下若用线性变化和激活函数代替邻域节点聚合操作便能在图分类任务上取得很好的效果。
3 实验数据与指标评判
3.1 实验参数设置
Keras模型有两种:序贯模型和函数化模型。序贯模型是层对象堆叠得到的网络模型,序贯模型不显示定义输入层,因此在添加第一层时需要指定输入数据的大小;函数化模型是将两个张量分别定为输入和输出,并且将与输入张量和输出张量相连接的节点组合成神经网络模型,函数化模型显示定义了隐含层的张量,因此可以更容易地搭建非序列化模型。
由于之前模型中存在算法收敛速度不够快和冲过局部极值等情况,采用了更小的卷积核和更深的模型参数设置。
实验中将文中方法与两种不同的基于模型的静态方法和一种学习的方法进行比较:CVM模型考虑到每辆车都以与观察到的最后一帧相同的速度(横向和纵向)继续运动;而IDM是微观交通模拟的常用驱动程序模型,因为它可解释且无冲突,用它来预测纵向速度的变化并保持车道内位置恒定。
IDM的加速度是根据free road和interaction项计算得出的。自由道路加速度计算公式如式(5)所示。
(5)
在最大加速度amax的情况下,加速度指数和期望速度v0是可调参数,而当前速度v交互项aint定义为:
(6)
到前车的最小距离s0,时间间隔τ和最大减速度b是可调参数。v是车辆的速度,是其前身的闭合速度。总加速度是自由道路和交互作用加速度之和。由于IDM仅输出纵向加速度,因此在使用IDM时假设没有横向运动获取NGSIM数据集的IDM参数,对于HighD数据集,使用引导的随机搜索对IDM的参数进行了调整,总共有20 000个样本,数值对比如表1所示。

表1 IDM的优化参数
除了考虑相互作用的模型外,还添加了一个简单的前馈神经网络,仅根据自运载工具的过去数据预测轨迹。使用此基准模型来衡量通过将交互包括到模型中而获得的改进。
3.2 模型配置
每个模型都使用类似的配置:两层产生256维特征表示,然后是前馈层,产生最终输出; 所有模型都使用ReLU非线性激活函数,以避免梯度爆炸和梯度消失问题。GAT采用了四个关注头,每个都有64维特征表示。
由于GNN模型使用两层,因此它们的有效接收场是自我传播工具的两跳邻域。所有模型均以固定长度的时间步接收输入并产生输出,而不会重复发生。它们经过训练可以预测相对于最后位置的位移,并接收每个过去时间步的位置和速度。它们训练以使所有输出的均方误差最小。
在实验过程中,为了克服激活函数存在的参数更新速度非常慢,甚至会造成离期望值越远,更新越慢的现象,因此在实验过程将激活函数改为交叉熵损失,此时梯度不再跟激活函数的导数相关,收敛较快,且整个权重矩阵的更新都会加快。
3.3 实验结果与指标评判
为了验证模型与算法优化结果,以某物流公司的应急调度数据为系统测试:假设目标城市C有5种需要物资,分别为P1、P2、P3、P4、P5,需要调用物资数量分别为2 100、4 000、1 000、840和920,物资调度可用相邻6个物资储备仓库分别为S1、S2、S3、S4、S5、S6。到C所需时间为10、13、21、17、29、18。在文中的优化神经网络调度模型中,可以依据场地、交通情况、需求紧张等参数,以优化的调度算法实现最短途径网络运输图,同时神经网络权值系数和阈值经过优化更新,避免神经网络陷入局部最小。
在实验中,通过测量地面真实情况与预测之间的位置误差来报告模型的性能。报告了五秒钟的平均位移,每个时间步均加权,五秒钟后的最终位移。为确保有意义的结果,使用随机选择的随机种子将每次评估重复。在表2中,三组实验的比较数据将所有结果报告为平均标准偏差。
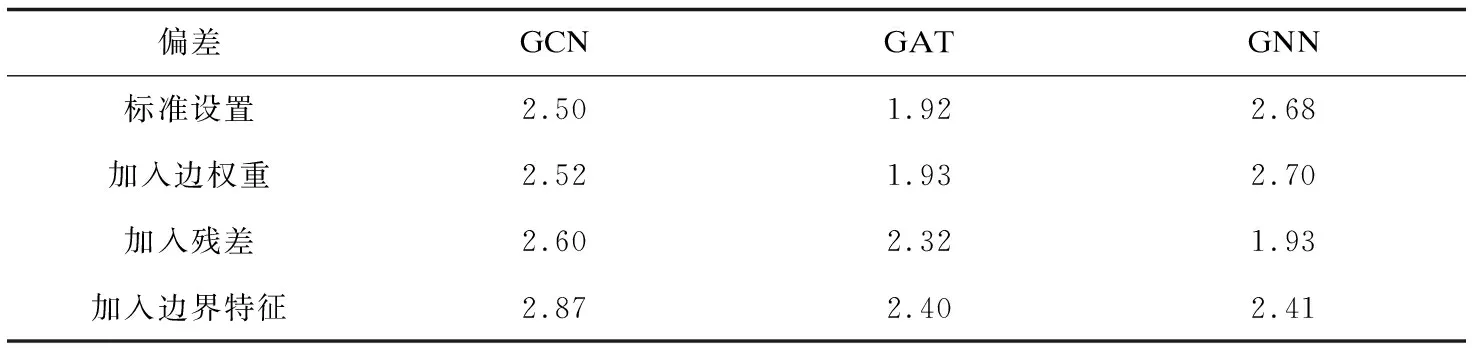
表2 实验数据比较
表2中显示了选择不同方法时不同的最优选择:若在标准设置条件下,GAT方法取得最小偏差1.92;在加入边权重条件下,GAT方法取得最小偏差1.93;在加入残差条件下,GNN方法取得最小偏差1.93;在加入边界特征条件下,GAT方法取得最小偏差2.40。
从实验过程总结可以发现,充分提取结构信息可以更好地提升神经网络模型效果,同时节点的度是一个非常重要的特征,也能够显著提升模型效果。
4 结束语
文中将交通场景建模为互动车辆的图数据,从而获得了灵活而抽象的交互模型,以预测未来交通参与者的行为。使用图神经网络,用于图数据的神经网络构建。实验中评估了三个计算有效的图神经网络方法并针对方案提出了三种改进方案。在具有丰富互动(包括互动)的流量数据集中与之前相比,将预测误差降低了30%以上,达到了最佳基准模型。同时,没有看到几乎没有交互作用的数据集的预测误差增加。
尽管提高了预测质量,但仍有很多工作尚待完成:这项工作仅完成了理论实验性验证,还有待进一步在实际复杂交通场景中进行预测优化。将此模型整合到现有模型中最先进的方法,尤其是RNN,仍然是开放任务。同时,想探索其他图构造策略,尤其是自动寻找相关的互动。但同时,该实验数据对于计算现实交通场景的复杂度仍具有挑战性,尤其在交通环境出现突发干扰偏差时。能够具有瞬时处理突发情况的动态模型,仍是研究的突破点和长久攻坚方向。

