支持LSSS访问结构的属性基群签名方案的研究
许玉岚,陈燕俐,高诗尧
(南京邮电大学 计算机学院、软件学院、网络空间安全学院,江苏 南京 210003)
0 引 言
属性基群签名(attribute-based group signature,ABGS)是对传统群签名(group signature,GS)的一种扩展,通过对群成员的身份特征进行划分,赋予用户不同的“属性”,这些“属性”可以用来标识群成员所拥有的权限,因此可以通过规定具有某些属性的群成员签署签名,来对签名者的权限进行限制,不符合要求的群成员生成的签名将被验证为无效签名。因为属性基群签名是将基于属性的签名[1](attribute based signature,ABS)与传统的群签名相结合,因此访问结构的选择与方案的好坏有着直接的关系。而目前属性基的群签名都是基于访问树结构的情况,树结构能够表示灵活的访问控制策略,但其安全性证明仅基于一般的群假设,但因为访问结构表示为一棵树,因此需要使用递归来进行运算。而递归的深度达到一定的程度时,程序的运行时间空间将受到一定影响。而LSSS访问结构很好地解决了这个问题。LSSS利用线性秘密分享方案的秘密可线性重组的性质重构秘密,不需要进行递归操作,提高了属性基签名方案的签名和效率,并且LSSS与访问控制树的表达性相当。因此,文中首次提出了一个支持LSSS访问结构的属性基群签名方案。
1 相关工作
1.1 群签名
自Chaum和Heyst[2]首次提出了群签名的概念,学者对群签名方案的研究包括增加各种功能,定义不同的安全概念以及提高方案的性能。
2000年,Ateniese、Caneniseh、Joye和Tsudik[3]使用交互的零知识证明(non-interactive zero-knowledge proof,NIZK)构造出第一个高效的、抗联合攻击的群签名方案,并且给出了随机预言模型下的安全性证明。Bellare,Micciancio等人[4]给出群签名的两个核心安全性质为强匿名性和强可追踪性。简化了群签名方案的安全性证明,即只需证明方案满足这两个安全性质。
2007年,Boyen,Waters[5]在标准模型下提出了群签名,该方案的基本思想是基于层次签名,即成员证书是第一层签名(即GM对用户身份的签名),利用第一层签名作为密钥,用户可生成第二层签名(即对某信息的签名),此签名还不可作为群签名,还需利用承诺方案对签名进行匿名化,最后利用标准模型下的NIZK证明承诺中的隐藏内容是合法的签名。
2019年,李雪莲等人[6]提出适合群成员数量较大的动态群签名,该方案利用群管理员或群成员本人与撤销图灵机通信,图灵机确定其身份后将撤销令牌添加到撤销列表即完成了撤销操作。2020年,叶青,杨晓孟等人[7]提出NTRU格上抗量子攻击的群签名方案,该方案利用NTRU格密码体制所需公私钥长度更短,运算速度更快的特点,构建了一个系统公钥长度小,计算效率高的群签名方案。张绪霞等人[8]于2020年提出一个基于中国剩余定理的前向安全群签名方案,该方案可以动态地增加和删除群用户成员而无须频繁更改群公钥,并在验证签名和打开签名时只需要进行模运算即可实现,同时针对密钥泄露问题实现了前向安全性。欧海文等人[9]于2020年提出一种具有前向和后向安全性的高效群签名方案,通过添加随机数的方式打破了公钥状态列表中公钥和私钥的直接联系,规避了被撤销成员联合得出其他成员私钥的风险,且群成员私钥随时间段跨越而自然更新(群管理员的私钥也因应改变),避免以往群成员发生私钥泄漏后需要重新选取密钥对才能保证后续签名安全性的繁琐过程。
1.2 属性基群签名
2007年,Khader[10]将传统的群签名方案进行了扩展,利用属性基的签名技术与群签名方案相结合,提出了属性基群签名。和属性基签名方案相同,用户是由属性集合表示,所以验证者并不知道群中用户的身份信息,只知道其相关属性,这样做到了对用户身份信息的隐私保护。与一般属性基方案不同的是,属性基群签名中的签名者在需要的时候可以由群管理员揭示。2008年,Khader在文献[11]中对上一方案进行了改进,实现了对群中用户的撤销和对属性的删除操作,使之更接近实际应用。
Emura等人[12]于2009年提出了动态的属性基群签名方案,其中允许访问结构树可变。2013年,Syed,Amberker[13]等人提出了一种具有属性匿名性和具有恒定签名大小的跟踪功能的ABGS方案,并证明了它在标准模型中的安全性。该方案的构造使用成员资格证书格式来实现标准模型中的不可陷害性,并使用Groth-Sahai[14]非交互式证明系统为标准模型下的群签名中的关系生成非交互式目击者不可区分性(NIWI)证明。
2017年,基于Merkle类的访问树,Kuchta[15]等人首次给出了基于格的属性基群签名方案,该方案同时具有加入和撤销机制,但该方案撤销成员时需要更新哈希树,计算复杂且耗时较长,并且该方案的签名长度与群成员数量相关。2019年Perera,Nakamura等人[16]提出了一种具有高效跟踪机制的新型VLR-ABGS方案。使用静态群签名方案中使用的跟踪算法来跟踪签名者及其在该方案中用于签名的属性。还使用群管理员的公钥来加密签名者的身份及其属性。因此,只有群管理员才能识别签名者和签名者的属性。2020年张彦华等人[17]针对本地验证者撤销的属性基群签名群公钥尺寸过长、空间效率不高的问题,采用身份编码技术对群成员身份信息进行编码,减少群公钥长度,通过单向和单射的带误差学习函数来完成撤销。
1.3 文中贡献
文中提出一种支持LSSS访问结构的属性基群签名方案,具体贡献如下:
(1)方案签名采用LSSS访问结构,效率更高。因为访问结构需要使用递归来进行运算,递归的深度达到一定的程度时,程序的运行时间空间将受到一定影响。本方案利用线性秘密分享方案的秘密可线性重组的性质重构秘密,不需要进行递归操作,且LSSS与访问控制树的表达性相当。
(2)实现了签名属性匿名性且签名长度固定。一般属性基群签名中将签名属性与签名一起发送给验证者,方案利用Groth-Sahai非交互式证明系统实现了签名属性的匿名性。并且方案使签名长度和计算开销是固定值,与签名者的属性数量无关,减少了通信和计算开销。
(3)实现了属性可追踪性。在上述具有属性匿名性的ABGS方案的基础上,提出了属性追踪,在发生用户滥用签名权限时,不但可以追踪到用户的身份,还可以追踪到用户具有的属性和签名的属性。
2 预备知识
定义1. 双线性映射(bilinear maps)[3]:设G1,G2,GT是阶为素数p的乘法循环群,g1,g2分别是G1,G2的生成元,存在一个具有如下性质的双线性映射e:G1×G2→GT:
(a)双线性:对于任意的u∈G1,v∈G2,a,b∈Zp,有e(ua,vb)=e(u,v)ab;
(b)非退化性:G1,G2中存在g1,g2,满足e(g1,g2)≠1。
这里的双线性映射被认为是type-3映射:同构映射ψ:G2→G1及其逆ψ-1:G1→G2都不能有效计算。
定义2. 线性秘密分享方案(linear secret sharing schemes,LSSS)[17]:设={p1,p2,…,pn}为n个参与者集合。一个上的秘密共享方案∏被称为Zp上线性秘密共享方案,如果满足以下条件:
(1)每个参与者的秘密份额构成Zp上的一个向量。
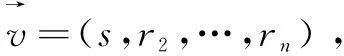
根据上述定义的线性秘密共享方案具有线性重构性质,其定义如下:设∏为访问结构上的线性秘密共享方案,S∈为授权集合,定义I={i,ρ(i)∈S}⊆{1,2,…,l},如果{λi}是参与者ρ(i)根据∏关于s的有效秘密份额,则存在多项式时间算法计算得到常数向量{wi∈Zp,i∈I},使得从而使得
定义3. DL[13](discrete logarithm)假设:已知G1是一个阶为素数p的双线性群,随机选择g∈G1,ξ∈Zp,对所有多项式算法A,下面的优势是可忽略的:
Pr[A(g,gξ)=ξ]
定义4. SXDH假设[18]:在群G1和G2上的DDH问题都是困难的,即不能有效计算同构映射ψ:G2→G1及其逆ψ-1:G1→G2。
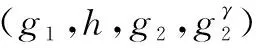
3 形式化定义与安全性定义
3.1 形式化定义
具有用户和属性匿名及追踪功能的ABGS方案由以下6个多项式算法组成:
(a)Setup(1k)→(params,ik,okuser,tkatt):输入安全参数1k,输出公共参数params,群密钥ik,用户打开密钥okuser和属性追踪密钥tkatt。
(b)UserKey(params,ik,Atti)→ski:输入公共参数params,群密钥ik,用户属性集Atti⊆Att。输出用户成员私钥ski,最新的成员注册表reg。
(c)Sign(params,ski,m,Υ)→σ:输入公共参数params,用户成员私钥ski,消息m,访问结构Υ,输出群签名σ。
(d)Verify(params,m,Υ,σ)→0/1:输入公共参数params,信息m,访问策略Υ,群签名σ,返回是否接受该签名。
(e)OpenUser(params,okuser,m,reg,σ,Υ)→(i,Atti)/⊥:输入公共参数params,用户打开密钥okuser,消息m,访问结构Υ,群签名σ,群成员列表reg,返回身份i和用户的属性集Atti或者⊥。
(f)TraceAtt(params,tkatt,m,σ,Υ)→ζ/⊥:输入公共参数params,属性追踪密钥tkatt,信息m,访问策略Υ,群签名σ,返回签名属性集合ζ/⊥。
3.2 安全性定义
定义6. 正确性:当满足下列条件时,可认为该属性群签名方案是正确的:
对于所有的Setup(1k)→(params,ik,okuser,tkatt),UserKey(params,ik,Atti)→ski,Υ,m∈{0,1}*,如果σ=Sign(params,ski,m,Υ),则:
成立。
在以下定义中,对手可以运行协议:
(1)通过JoinP-oracle,这意味着它创建了一个不知道其私钥的诚实用户:将索引i添加到HU(诚实用户)列表中。
(2)通过JoinA-oracle,这表示它将与群管理员交互以创建它控制的用户:将索引i添加到CU(不诚实用户)列表中。
当对手被赋予群密钥(群管理器已不诚实)时,对手不需要访问JoinA-oracle,因为它可以自己模拟来创建不诚实用户(不一定在CU)。创建用户后,对手扮演不诚实用户的角色,并可以与诚实的用户交互,授予一些预言:
(1)corrupt(i):如果i∈HU,则提供此用户的特定私钥。对手可以在整个模拟过程中对其进行控制。将i从HU转移到CU中。
(2)sign(i,m,Υ):如果i∈HU,作为诚实的用户i将在签名过程中使用访问结构Υ在消息m上生成签名。
(3)openusr(m,σ,Υ):如果(m,σ,Υ)是有效的,则返回签名者的身份i和属性集Atti。
(4)tratt(m,σ,Υ):如果(m,σ,Υ)是有效的,则返回用于生成签名的属性集ζ。
定义7. 属性匿名性:对于所有多项式时间算法A,A赢得以下游戏的概率是可以忽略不计的,则称该方案具有属性匿名性。
初始化:挑战者C运行Setup(1k)→(params,ik,okuser,tkatt),并将(params,ik,tkatt)发送给A。
第一步:A被赋予询问joinP,corrupt,sign,tratt预言的权限。
挑战:A输出信息m*,访问结构Υ*,诚实用户Ui(即i∉CU),则∃ζi0,ζi1⊆Atti,Υ(ζi0)=1,Υ(ζi1)=1成立。C随机选择k∈R{0,1},并响应一个群签名σ*←Sign(params,ski,ζik,m,Υ)。
第二步:A可以进行类似于第一步的查询。但是A不能在任意时候对i进行corrupt查询。
输出:最后,A输出k',如果k=k'则获胜。A的优势定义Advuser-anon(A)=|Pr(k=k')-1/2|。
因此不存在任何多项式时间攻击者将群签名联系到用于生成它的一组属性。
4 支持LSSS访问结构的属性基群签名方案
4.1 角色分类
系统共有5个角色:群管理员(group manager,GM),用户,验证者,打开者(opener)以及属性追踪者(attribute tracer)
(a)群管理员:群管理员被认为是可以信任的,主要负责系统公共参数的生成,其次群管理通过群密钥与群成员交互为其发布密钥。
(b)用户:用户与GM进行交互,从而成为该群的成员,并且在满足访问策略的情况下代表该群进行签名,并将签名发送给验证者。
(c)验证者:在接收到群签名后,验证者可验证此签名的合法性,即是该群中的某一人签署了此签名,但不能确定具体的签名者。
(d)打开者:当发生用户滥用其签名权利时,打开者可以通过打开群签名找到签名者的身份和拥有属性。
(e)属性追踪者:可以追踪来自群签名的签名属性集,该属性集满足访问结构。
4.2 方案具体构造
(1)初始化Setup(1k)→(params,ik,okuser,tkatt)。
由群管理员执行,具体步骤如下:
(a)生成阶为q的循环群G1,G2和GT,双线性映射e:G1×G2→GT,g1,g2分别是群G1,G2的生成元。
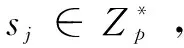
(d)选择生成元h,u0,…,un∈G1,定义Water函数[16],:{0,1}m→G1,即对M={μ1,…,μm}∈{0,1}m,
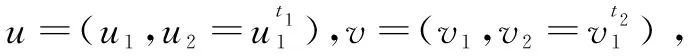
最后生成公开参数params,群密钥ik,用户打开密钥okuser和属性跟踪密钥tkatt如下:
params=(q,G1,G2,e,g1,g2,Att,,h,u0,u1,…,um,Z,u,v)
ik=(S={sj}attj∈Att,α),okuser=α1,tkatt={Qj}attj∈Att
(2)用户密钥生成UserKey(params,ik,Atti)→ski。
用户与群管理员交互执行,用户可通过公私钥(upki,uski)和群管理员之间进行信息的交互。具体步骤如下:

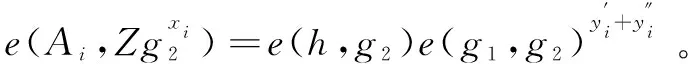

(e)用户检验e(Xi,1,g2)=e(Xi,2,g1),验证通过后,用户拥有有效的成员证书(Ai,Xi,yi)和属性证书{Ti,j}∀attj∈Atti。
最后,用户获得私钥ski={(Ai,Xi,yi),{Ti,j}∀attj∈Atti,{sj}∀attj∈Atti},GM获得最新的群成员列表reg。
(3)签名Sign(params,ski,m,Υ)→σ。
由用户执行,具体步骤如下:
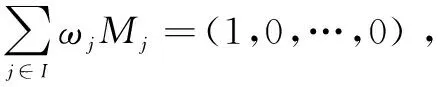
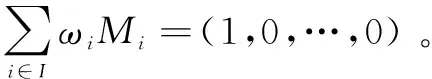
(e)对群元素进行承诺得到σi=(ρi),i={1,3,4},σ2=((1)(ρ2),(2)(ρ2))。
(f)计算NIWI Groth-Sahai证明[13]的承诺变量ρ1,ρ2,ρ3,ρ4满足下列等式:
(1)
e(ρ4,Zρ3,2)=e(h,{Tk}k∈{1,n'})
(2)
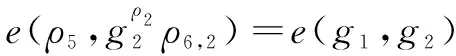
(3)
e(ρ7,g2)=e(h,ρ6,2)×e(F(m),ρ8)
(4)
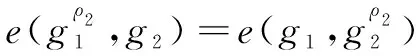
(5)
e(ρ3,1,g2)=e(g1,ρ3,2)
(6)
e(ρ6,1,g2)=e(g1,ρ6,2)
(7)
本方案通过签名上Groth-Sahai零知识证明,证明了上述映射等式的有效性。等式1是确定签名者具有通过用户密钥算法颁发的有效成员证书(即Ai格式正确);等式2确定签名者具有满足访问结构Υ的属性,并且证明了成员证书与属性证书相关联;等式3证明了ρ5正确(即用户的身份ID正确);等式4不需要任何承诺,因此可以直接验证该签名(ρ7,ρ8)是在密钥ρ6下对M的有效签名;等式5、6是确保可追踪对手模型中需要的yi,Xi的正确性;等式7用于在不可陷害性对手模型中进行检测。
(4)签名验证Verify(params,m,Υ,σ)→1/0。
由验证者执行,根据Groth-Sahai证明验证所有的等式是否成立,若成立返回1则说明该签名有效。若不成立则返回0表示不接受该签名。
(5)打开OpenUser(params,okuser,σ,m,reg,Υ)→(i/Atti)/⊥。
由打开者(Opener)执行,对于有效的群签名,打开者只需在签名σ中打开Ai的承诺,并在群成员列表reg中找到与Ai对应的身份i和属性Atti,否则输出⊥。
(6)属性追踪TraceAtt(params,tkatt,m,σ,Atti,Υ)→ζ/⊥。
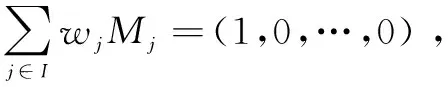
5 安全性分析与性能分析
5.1 安全性分析
文中方案具有属性匿名性、用户匿名性、可追踪性、不可伪造性、属性抗联合攻击性及属性不可伪造性,但因篇幅,仅给出了属性匿名性、可追踪性证明,其他证明见完整版。
定理1:文中方案具有正确性。
证明:
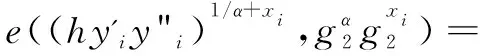
此等式成立表示签名者拥有通过密钥生成算法颁发的有效成员证书;
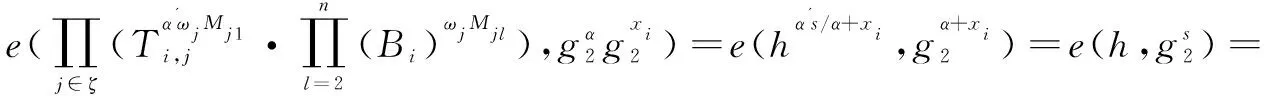
e(h,{Tk}k∈{1,n'})
此等式成立表示签名者拥有满足访问结构的属性证书;
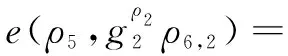
此等式表示签名者的身份是正确的;
e(hzF(m)r,g2)=e(hz,g2)×e(F(m)r,g2)=
e(h,ρ6,2)×e(F(m),ρ8)
此等式表示该签名是在密钥ρ6下对m的有效签名;

对于诚实的用户来说,根据零知识证明的完备性,拥有成员证书和属性证书的诚实用户始终可以生成一个有效的证明。通过以上分析,合法的签名总是可以通过验证,根据定义该方案满足正确性定义。
定理2:文中方案在SXDH假设下具有属性匿名性。
证明:该证明来自Groth-Sahai证明系统。也就是说属性隐藏在ρ4中,且用Groth-Sahai证明技术承诺到σ4中。因此,在SXDH假设下,它是完全隐藏的。
定理3:如果存在伪造属性签名通过验证的攻击者A,那么就存在一个可以破坏DL和KEA假设的攻击者B。
初始化:该ABGS方案初始化阶段模拟器B生成系统参数params。B设置g1=g,h=g',生成其余参数(ik,okuser,tkatt)。并将(params,ik,tkatt)给攻击者A。
查询:由于B知道所有的密钥,它可以根据属性不可伪造性的定义响应攻击者A产生的所有查询。
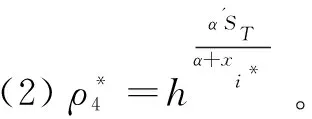
5.2 性能分析
首先对本方案与现有属性基群签名方案进行功能上的比较,结果如表1所示。文献[11-13]方案都是采用访问树结构,访问树结构因为要采用递归运算,因此计算效率较低。本方案在提供了细粒度访问控制的同时支持LSSS访问结构,LSSS利用线性秘密分享方案的秘密可线性重组的性质重构秘密,且LSSS与访问控制树的表达性相当。由于不需要递归运算,因此计算效率较高。文献[11-12]不具备属性匿名性和属性可追踪性,与文献[11]方案的属性可追踪性相比,本方案不仅可以追踪到签名用户的属性集,并且还可以追踪到用户签名属性集,即该用户签名时符合访问结构的子属性集合。

表1 方案功能比较
本方案与现有属性基群签名方案效率比较如表2所示。设n表示与签名相关的属性数,l表示用户的属性数。通过对比发现,文献[11-12]的签名大小和验证计算开销都与签名属性数相关,而文献[13]和文中方案的签名大小和计算开销均为固定值,与属性数无关。虽然文献[13]和文中方案的签名计算开销复杂度相同,但文献[13]的方案在签名前需要构建一个冗余访问树,并且其为满足访问树可变,添加了冗余节点,增加了存储开销。而且在生成签名时,需要使用拉格朗日插值法,因此签名计算开销要大于文中方案,但文中方案在验证计算开销和满足签名策略的属性集合数相关,因此验证开销大于文献[13]方案。

表2 方案效率分析
6 结束语
文中实现了一种支持LSSS访问结构的属性基的群签名方案。该方案不仅降低了计算开销,实现了属性匿名性,并且在发生用户滥用签名权利时,不但可以追踪到用户的身份和属性,还可以追踪到用户签名属性。方案的签名长度和验证计算开销均和属性数量无关,具有良好的通信和计算开销。文中的构造是基于双线性对的,随着量子计算机的到来,此类方案的安全性将受到威胁,而格密码系统不仅可抵抗量子计算攻击,安全性更高,因此在未来的工作中,将对格上基于LSSS访问结构的属性基群签名方案进行研究。

