频率域电磁波优化25点有限差分正演模拟

中国电子科技集团公司第二十研究所 李宏亮 党 杰

时间域电磁波有限差分方法(FDTD)是一种常用的电磁波数值模拟方法，通过将电磁波进行网格化处理，使得电场和磁场均匀的分布在网格上，从而求解电磁波方程。本文基于麦克斯韦方程组，开展了基于频率域电磁波有限差分的相关研究。为了验证频率域有限差分的可行性以及提高数值模拟精度，主要采用了两种方法：第一种方法是在麦克斯韦方程组的基础上直接推导出频率域电磁波方程，避免了时间域递推造成的累计误差；第二种方法是采用优化25点差分方法构建频率域电磁波方程算子，不仅保证了模拟的精度，而且能有效的抑制数值频散。此外，为了验证算法的可行性，在PML边界条件下进行了频率域电磁波的数值模拟。

随着电磁波理论研究与实际应用的推广，麦克斯韦方程组的数值解法也被广泛的关注和研究。已经提出的方法有频率域的矩量法、有限元法、有限差分法以及时间域的传输线矩阵法、有限差分等方法。各种方法都有自己的优势以及应用上的局限性，要么计算过于复杂，要么占用内存大、计算速度慢，在实际应用中往往需要将几种方法混合使用。

有限差分方法的中心思想是用差分代替微分，通过将研究区域网格化处理，使电场和磁场有规律的分布在网格点处，从而得到网格区域的电场和磁场值。本文通过推导麦克斯韦方程组得到频率域二维电磁波方程，然后整理成矩阵方程形式，采用优化25点有限差分方法构建频率域差分算子，对算子进行稀疏化存储，使得频率域数值模拟更加简便快捷，同时也证明了该方法的有效性。

1 频率域电磁波优化25点有限差分

1.1 频率域电磁波方程推导

麦克斯韦方程组的微分形式是这样的，如式(1)：

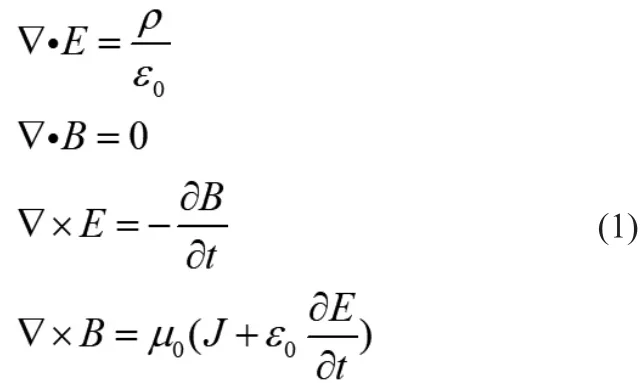
式(1)中，E表示电场强度，B表示磁场强度；ρ表示电荷密度，J表示电流密度；ε0和μ0分别表示真空中的介电常数和磁导率；是矢量微分算子，和分别表示求取散度和旋度。

为简化后续推导，考虑真空、均匀介质(即ρ=0，J=0)情况下，麦克斯韦方程组变为式(2)：

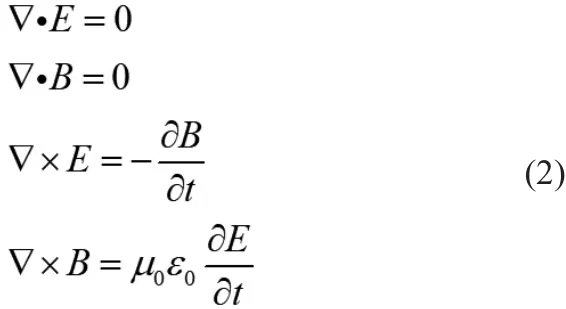
式(2)方程两侧同时取旋度，并作进一步简化，得到式(3)：

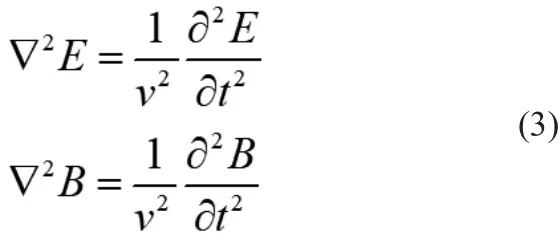
考虑二维情况，可以将式(3)改写为式(4)：

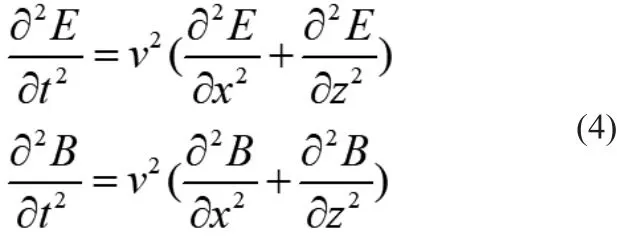
式(4)两侧对时间做傅氏变换，即：

式(5)中，ω表示角频率；和分别是电场强度和磁场强度的频率域表示。

1.2 基于优化25点有限差分方法的算子离散化

图1所示为优化25点有限差分方法中各个权系数分布示意图。在求解时，需要用到该点周围的25个点，而这25个点对于要求解的二阶差分算子“贡献程度”是不同的。如图1(a)，每一行需要用到5个点来构造2个差分算子，根据每一行中各列元素距离待计算点的距离远近，设置加权系数c、d，将他们结合起来作为这一行的差分算子，因此可以得到5个差分算子。然后，再将这5个差分算子通过加权系数b1、b2、b3进行加权平均即可得到最终的离散形式。同理，也通过类似的方法可以获得，如图1(b)所示。图1(c)是方程左端加速项的差分格式，其权系数以差分点为圆心，分布在一组同心圆上。

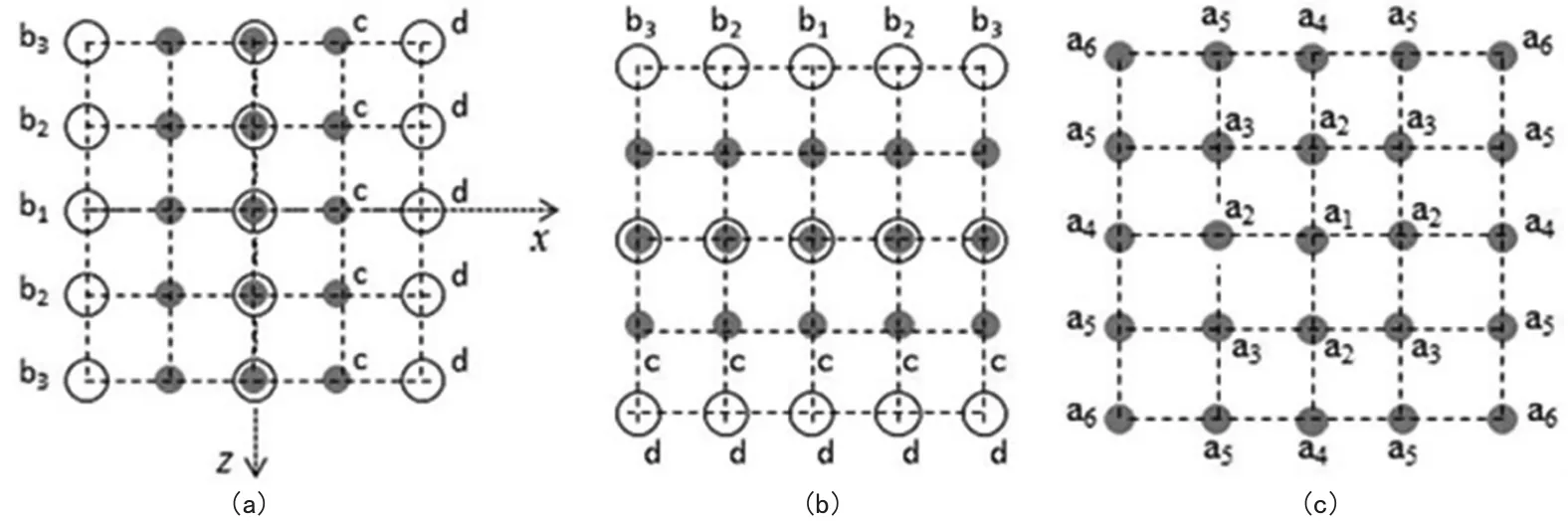
图1 优化25点差分示意图

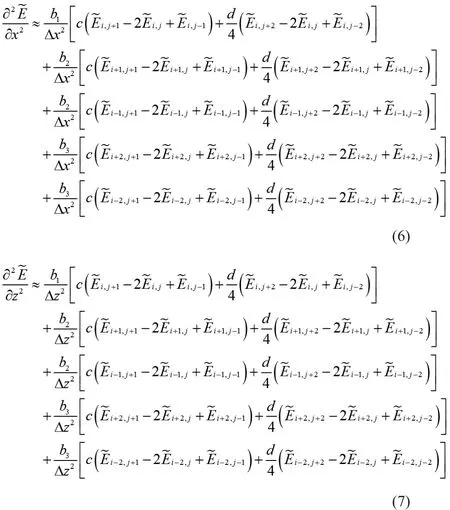
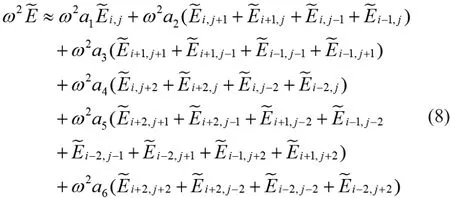
为了使网格色散和数值各向异性尽可能最小，必须确定一组最优的加权系数使相速度和群速度尽可能的接近。求取这些系数可以采用梯度法或牛顿法，通过给定一组初始值，不断地迭代搜索以使该系数能够同时使相速度和群速度接近。

本文采用Min利用高斯牛顿法计算出来的最优加权系数：

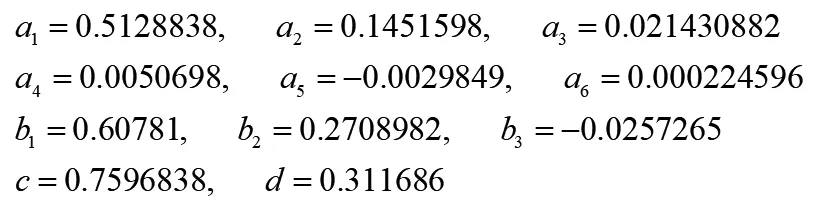
1.3 吸收边界条件及离散方程

电磁波在空间中传播时相当于是在一个半无穷的介质中传播，没有边界的影响。但在数值模拟过程中，由于计算区域有限，而且人为的引入了反射界面，这就会导致出现一些在实际中不会出现的反射波，影响最终的模拟结果。因此，必须构造一个吸收边界，以期望尽可能的抑制这种边界反射，从而更加真实的模拟电磁波的传播过程，研究电磁波的传播特性。

本文采用PML（如图2所示）吸收边界来抑制边界反射。当地震波传播到边界时，随着进入到吸收层内传播距离的增加，电磁波不断地衰减，这样当波传播到最外层边界时，其能量被完全衰减就不会产生边界反射。当电磁波传播到区域1时，沿x和z方向都衰减；当波传播到区域2时，沿x方向不衰减，沿z方向衰减；当波传播到区域3时，沿x方向衰减，沿z方向不衰减。

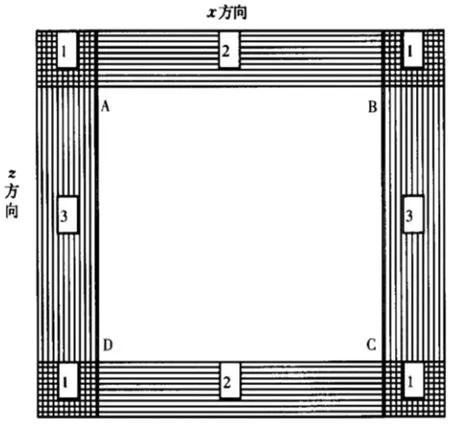
图2 PML吸收边界示意图(引自王守东,2003)

具体的，将这种边界施加到电磁波方程时，需要做一个坐标拉，这样施加PML吸收边界的电磁波方程就可以表示为式(9)：伸的变换

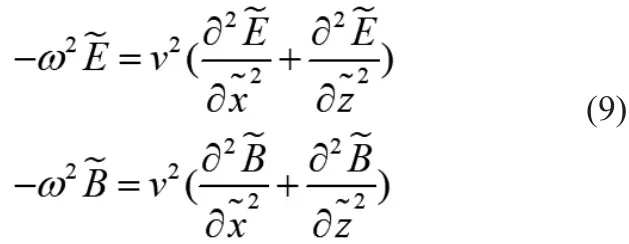
用d来表示衰减因子，使得PML吸收区域内d≠0，而有效计算区域内d=0。定义，得：

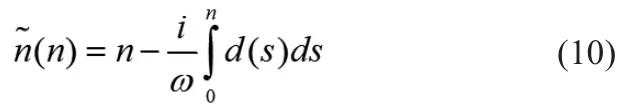
则：

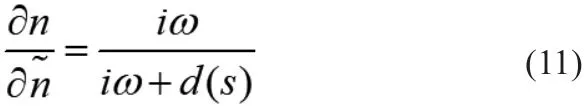
其中：

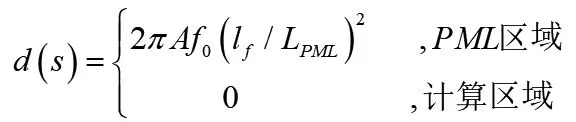
式中A是在0.5～1.79之间取值的常数，通常需要通过不断地试验确定最佳的参数，后文中数值模拟时采用A=1.3；f0是主频；LPML是PML层的厚度；lf是PML边界与内部有效计算区域的距离。

将衰减因子代入电磁波方程(5)式，得到：

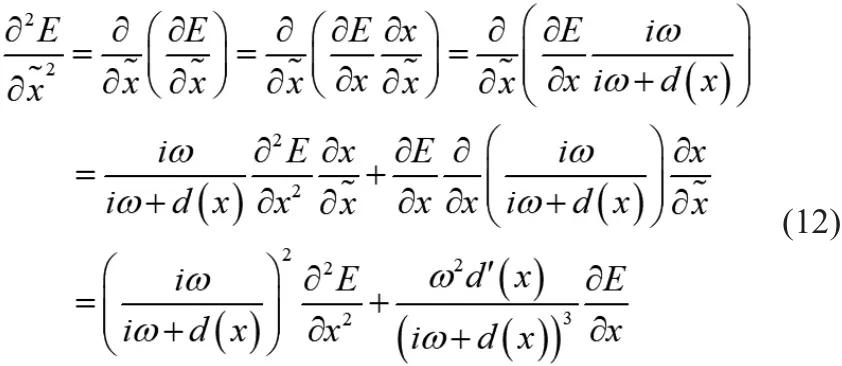
根据文献，为简化后续推导，通常省略式(12)中一阶偏导项，亦即：

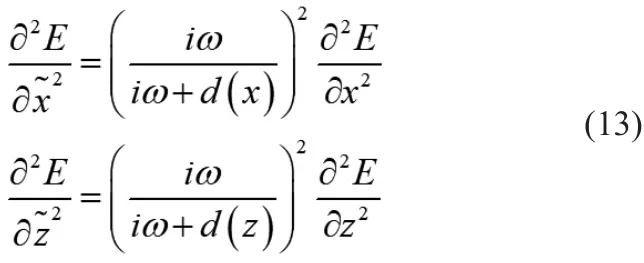
将差分加权系数以及式(10)～式(13)带入到式(9)中，施加PML边界条件，合并同类项后得到最终的离散方程为：

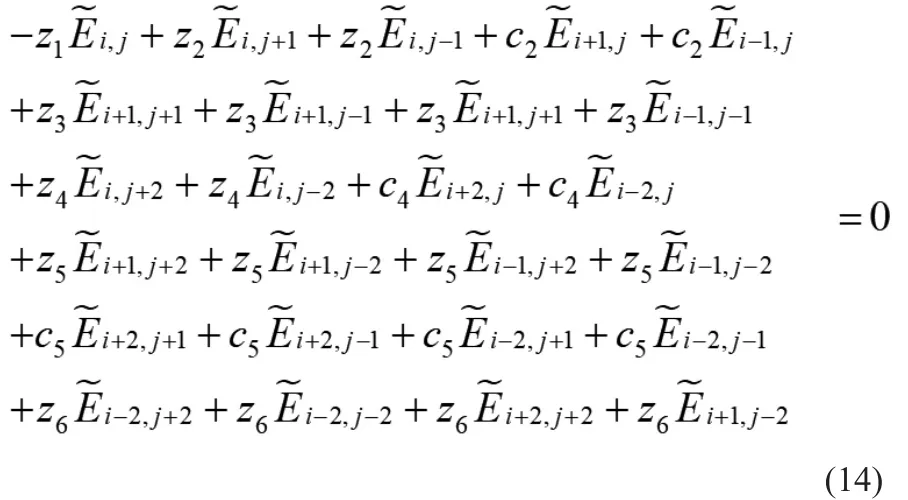
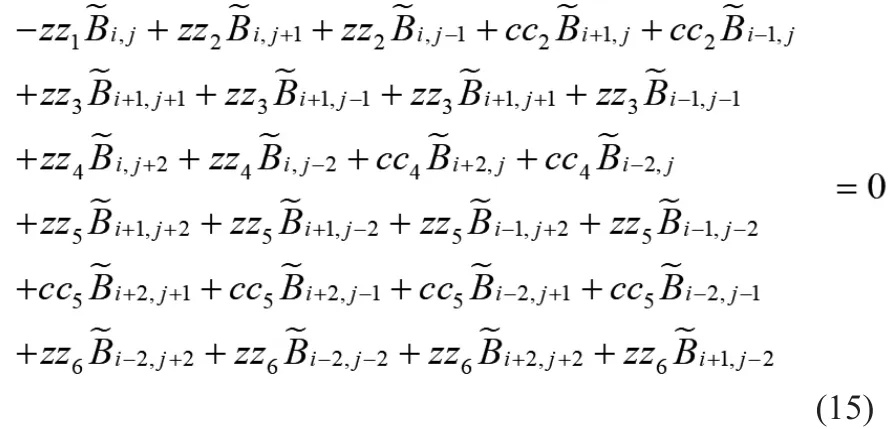
式中参数为：

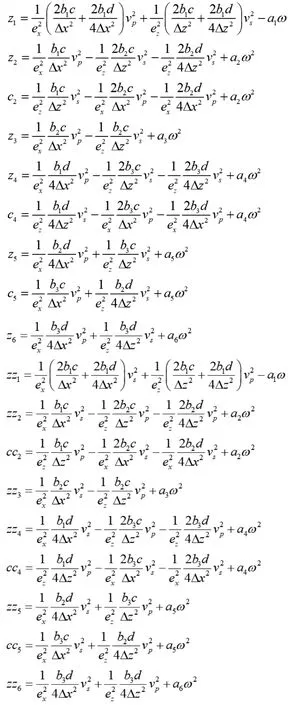
方便起见，将式(14)和式(15)联合起来整理成矩阵方程形式：

式(16)中，A是由差分系数构成的一个具有25条对角线的系数矩阵，该矩阵是一个大型的、非对称的稀疏矩阵；U是由和构成的一个列向量；F是施加的激发源。若网格区域为N=m×n，则A是一个2N×2N的矩阵，U是2N×1的向量，F是2N×1的向量。

2 数值模拟

2.1 数值模拟

为了验证各种激发源加载的有效性，在均匀各向同性介质中进行数值模拟实验。模型的网格大小为160×160，x和z方向的网格间距为dx=dz=0.005m。图3是激发源主频为3GHz，在模型中心位置处激发得到的单频切片。

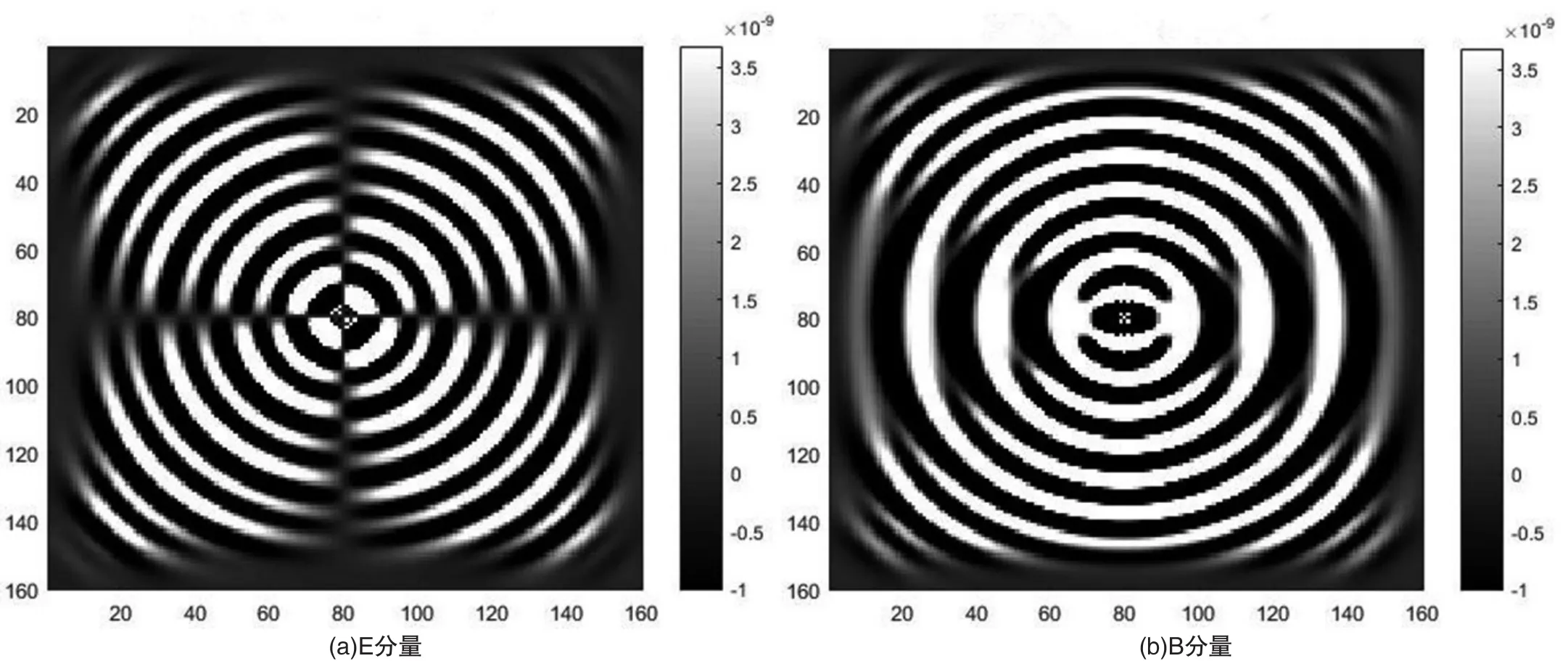
图3 集中力源单频切片

2.2 精度对比

为了测试差分点数对数值模拟精度的影响，在相同参数下，采用网格大小201×201，网格间距Δx= Δz=0.005m，激发源主频为3GHz，放置在模型中心处。根据式(16)分别采用9点差分方法和25点差分方法构建系数矩阵，进行电磁波正演模拟。图4是将频率域各个频点单频切片汇总后进行反傅里叶变换得到的时间域某时刻波场快照。可以看出，通过优化25点差分方法构建正演算子得到的模拟结果较之常规方法而言能够很好地抑制数值频散。

图4 波场快照

结论与展望：本文在麦克斯韦方程组的基础上，推导出了真空中电磁波的频率域表达式，并采用优化25点有限差分方法对电磁方程进行了差分，得到了基于优化25点有限差分方法的离散电磁场方程。通过添加PML边界条件，进行了频率域电磁波数值模拟，得到了以下认识和结论：

（1）采用25点有限差分方法进行电磁波数值模拟具有更高的精度；

（2）由于频率域系数矩阵只与差分系数有关，故系数矩阵A只需要计算一次，这使得频率域电磁波数值模拟计算速度快，很适合并行计算，为理论研究和工程实践提供了一个较好的实现思路，为电磁波成像和反演奠定了一定的基础。

当然，这种方法从目前来看仍有一定的限制，比如从二维模型转向实际三维模型时系数矩阵需要的巨大内存或者说是系数矩阵稀疏化如何处理，以及实际工程应用中大量的频率域数据如何转化等问题都有待进一步考虑。