高性能变传动比的异形齿轮跳跃机构研究*
刘 磊,张 岩
(1.包头钢铁职业技术学院 机械工程系,内蒙古 包头 014010;2.河北科技大学 机械工程学院,河北 石家庄 050018)
0 引 言
在机器人系统的机械设计中,常利用减速器来改变执行机构的性能,最典型的应用就是跳跃机器人。一般情况下,由于传动比是一个常量,机器人会根据运动和任务选择合适的传动比[1,2],例如当需要较大扭矩时,通过牺牲角速度来选择较小的传动比。但是,实际情况中,许多任务同时需要大扭矩输出和高速来实现[3,4],例如搬运重物等。针对这些任务,变传动比在连续运动方面是有效的,且不需要更换齿轮。
到目前为止,已有许多关于跳跃机器人的研究。ASILOPOULOS V等[5]提出了足部关节处的力多边形,根据每个关节上的力控制器来研究着陆特性。VERSTRATEN T等[6]提出了一种串联弹性双电机驱动的跳跃机器人。
但是,上述这些方法集中在稳定跳跃的控制上,无法实现大扭矩输出和高速度变化。因此,变传动比成为了目前研究的热门方向。BHATTI J等[7]提出了适用于敏捷跳跃机器人的自适应高度控制器。BAI L等[8]提出了仿生间歇跳跃机器人设计,并对其变传动比机构进行了动力学分析。
在上述这些机构中,机器人通过弹簧或惯性力积累的能量来实现更高的跳跃,但并非所有的能量都可用于跳跃,可能会消耗执行器大量能量,而降低电机运行效率。
因此,本文以有效利用电机功率为目标,提出一种跳跃运动最优变传动比的设计方法,并通过异形齿轮实现所获得的变传动比;同时,提出一种异形齿轮的齿形(节曲线)设计方法,并通过原型对该设计方法的有效性进行评价;此外还研究跳跃高度随机器人参数和初始姿态扰动的变化。
1 跳跃机器人与最佳传动比
1.1 传动比的优化
首先,需要推导出使地面作用力最大的最佳传动比。跳跃机器人机构及其运动示意如图1所示。
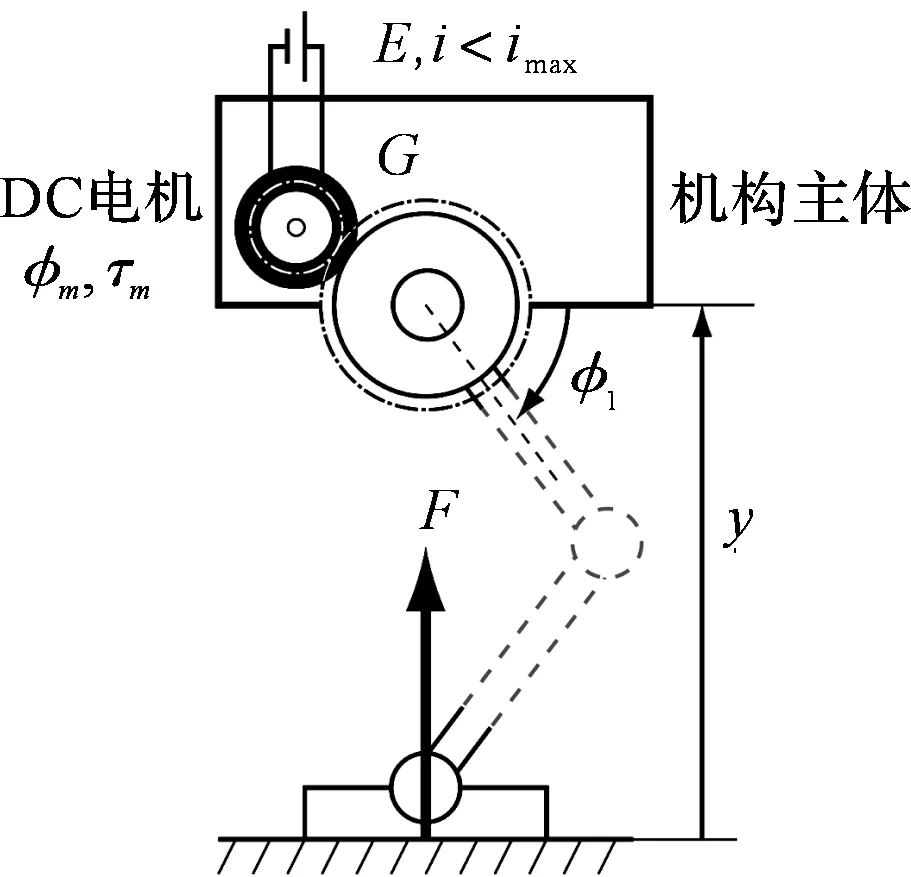
(a)跳跃机器人的机构
φm—电机的旋转角度;τm—电机的输出扭矩;EZC—电机供电的恒定电压;i—电机电流;imax—电机电流的最大值;φ1—腿部连杆的旋转角度;G—传动比;y—主体高度;F—垂直于地面的作用力
如图1(a)所示,直流电机安装在机器人主体上。
φm与φ1之间的关系如下:
(1)
本部分不考虑腿部机构的结构,但假定其φ1与主体高度y之间的运动关系为:
(2)
此外,由于运动学上的限制,机器人主体的运动被限制在垂直于踝关节和髋关节中心的垂直线上,如图1(b)所示,这表明机器人具有一个自由度。
电机扭矩τm产生垂直地面的力F,考虑最大化F来设计最佳传动比。
机器人的动能e表示为:
(3)
式中:yoff—机器人起跳时的主体高度。
机器人在F<0时起跳。F越大,则跳跃越高。
根据电机端子之间的电压关系[9],可推导出以下等式:
(4)
式中:R—电机电阻;L—电机电感;Ka—扭矩常数。
假设L可以忽略不计,则i表示为:
(5)
且τm可表示为:
(6)
另一方面,根据式(1,2)和虚功原理,F可表示为:
F=(GJ)-1τm
(7)
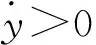
将式(2)和式(6)代入式(7),得到:
(8)
(9)
另一方面,电机功率P可表示为:
(10)
1.2 基于正向动力学分析的节圆半径设计
步骤1:机器人动力学由下式表示:
(11)
式中:Mm—惯性;Cm—离心项;Km—重力项。
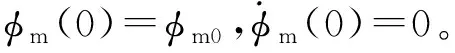
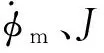
(12)
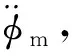
由式(1)对时间的微分可得:
(13)
由式(13)的二阶积分计算得到φl。
∂G/∂φm的近似值为:
(14)
式中:ΔG—当前迭代与前一次迭代之间的G差值;Δφm—当前迭代与前一次迭代的φm差值。
步骤4:根据式(8),使用式(2)计算F。当F>0时,转到步骤2,重复相同的过程;当F≤0时,停止迭代。
通过上述过程,可以得到的φm和G如图2所示。
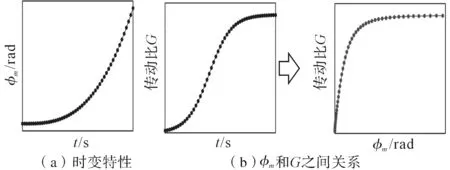
图2 得到的φm和G
φm和G的时间变化如图2(a)所示,且得到了φm和G的关系G=G(φm)如图2(b)所示。
将输入和输出异形齿轮中心之间的距离定义为d,输入齿轮rin的节圆半径可通过以下公式获得:
(15)
输入齿轮的节圆半径如图3所示。

图3 输入齿轮的节圆半径
输出齿轮rout的节圆半径也采用同样的方法得到。
2 跳跃机构与异形齿轮的设计
2.1 跳跃机构设计
在这一部分中,笔者为跳跃机器人设计了一个非圆形齿轮。跳跃机器人的结构如图4所示。
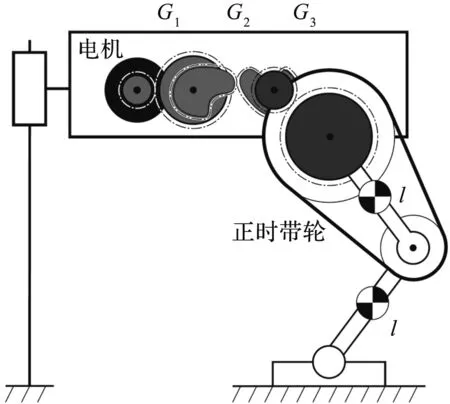
图4 跳跃机器人的结构
图4中:齿轮1、2和3的传动比分别为G1、G2和G3,其中,G1较小以增加扭矩,G2为由异形齿轮实现的变传动比,而G3大于1,以扩大异形齿轮的有效区域,因为腿旋转角度小于90°。对于该跳跃机构,图1(a)中的G由G=G1G2G3表示。主体的运动由线性滑块限制在垂直方向。大腿和小腿由正时带轮连接。正时带轮的传动比为2。
将大腿和小腿的长度设置为l,式(2)中的J由下式表示:
J=2lcos(φl+φI0)
(16)
最佳传动比G2由下式给出:
(17)
式中:φl0—φl的初始值。
2.2 异形齿轮的齿形设计
基于所提齿形设计方法,笔者设计了一种异形齿轮。异形齿轮不能实现零传动比,即具有最小传动比G2min。
G2min为0.1和1时的仿真结果对比如图5所示。
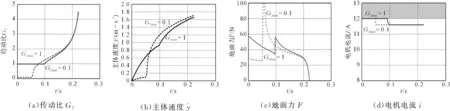
图5 G2min为0.1和1时的仿真结果对比
由图5可知:
(1)G2min为0.1时,传动比在运动开始时受到G2min的限制。如图5(a)中虚线所示:0.051 s之后,G2的变化较大,它的变化过大导致主体速度和地面力的变化很大,还产生了较大的轮齿压力角。
根据图5(b)中虚线所示,起跳时的主体速度为1.69 m/s,产生了0.124 m的跳跃高度。跳跃高度的定义如图6所示。
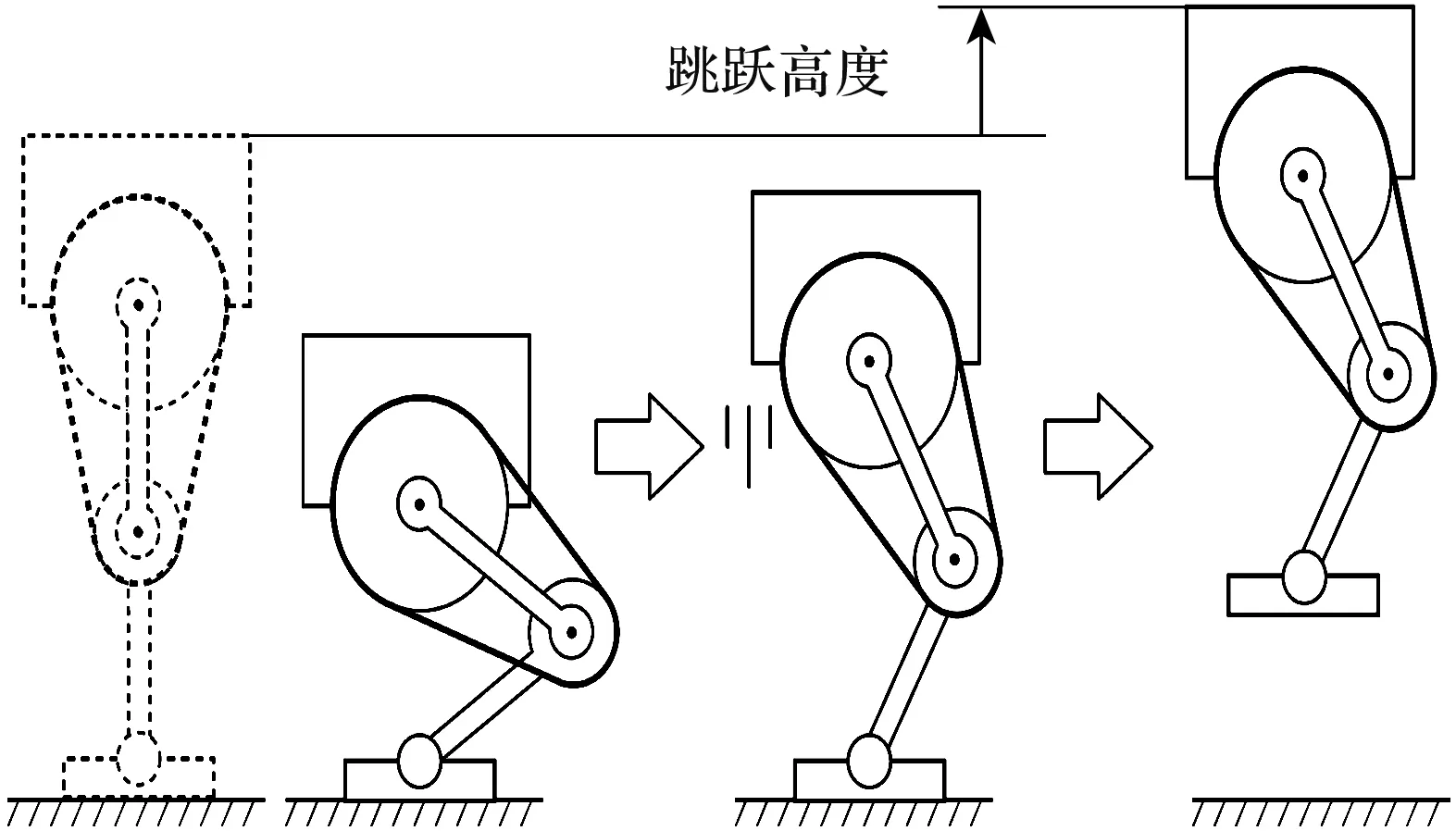
图6 跳跃高度的定义
由于受轮齿压力角的限制,异形齿轮无法实现所获得的传动比,因为G2min为0.1太小了;
(2)G2min为1时,机器人在0.221 s时起跳,主体速度为1.64 m/s,跳跃高度为0.117 m(仅比G2min为0.1时低5.6%)。
异形齿轮的齿形(节曲线)如图7所示。
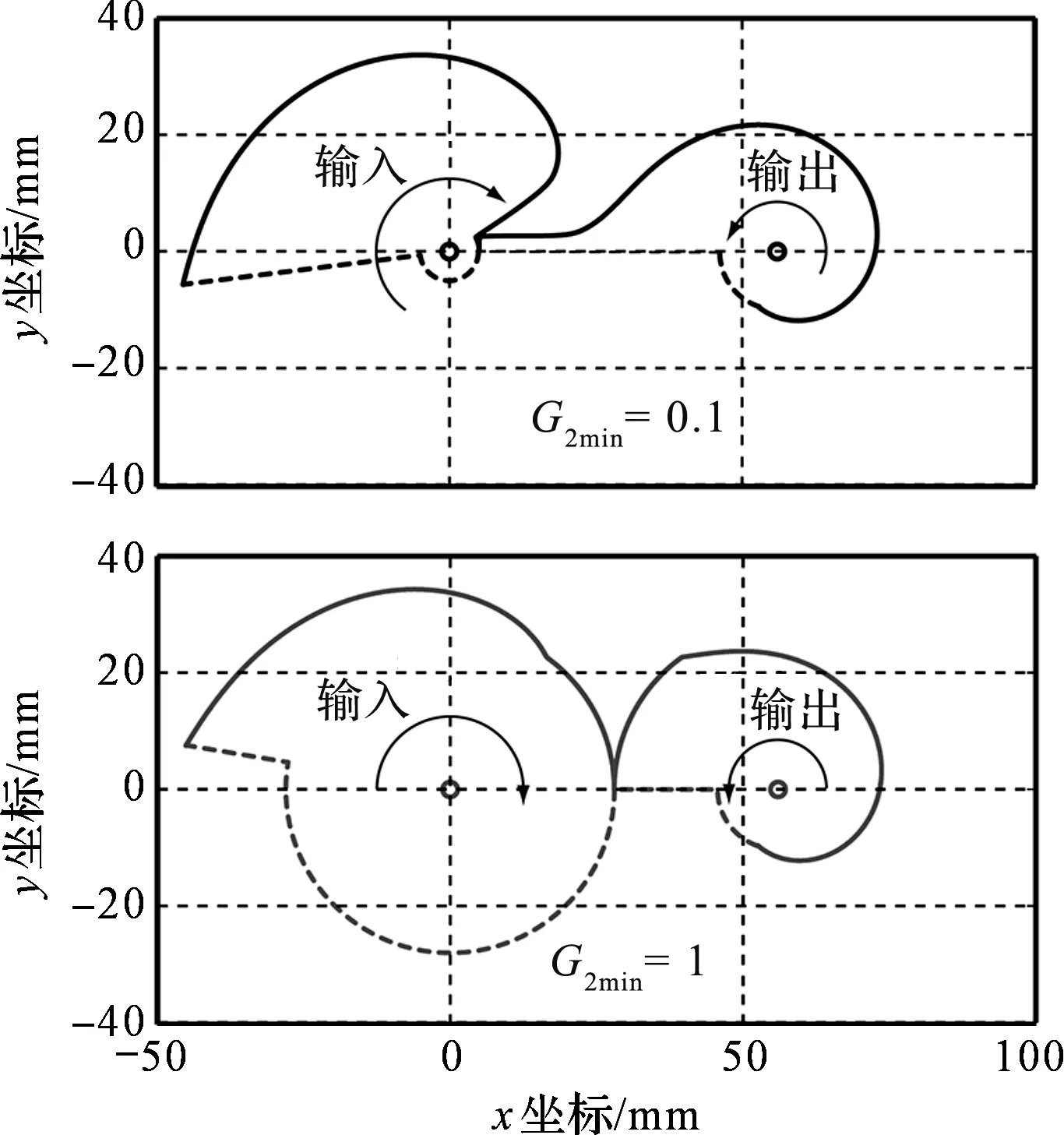
图7 异形齿轮的齿形(节曲线)
轮齿压力角如图8所示。
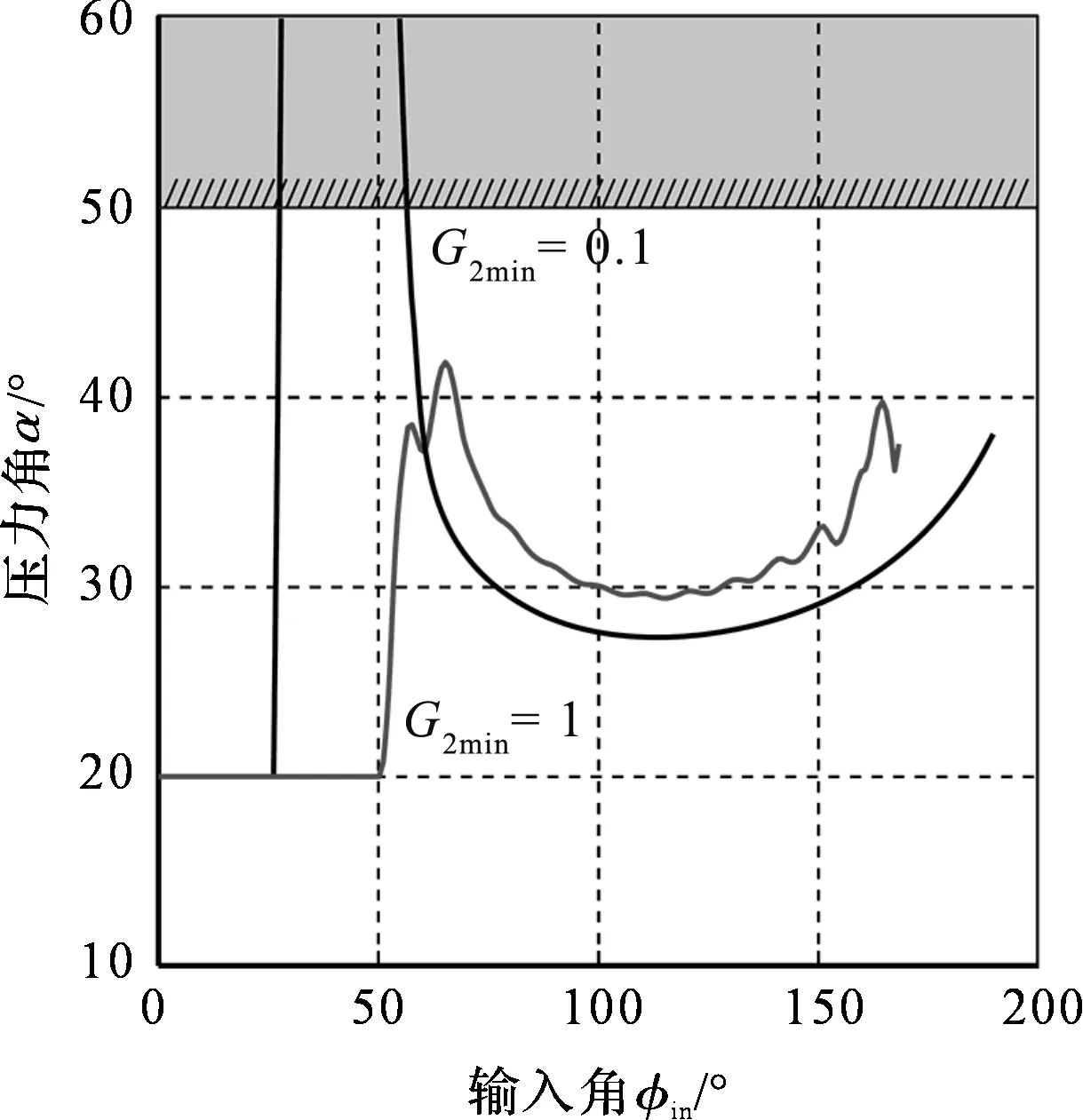
图8 轮齿压力角
压力角α的定义如图9所示。
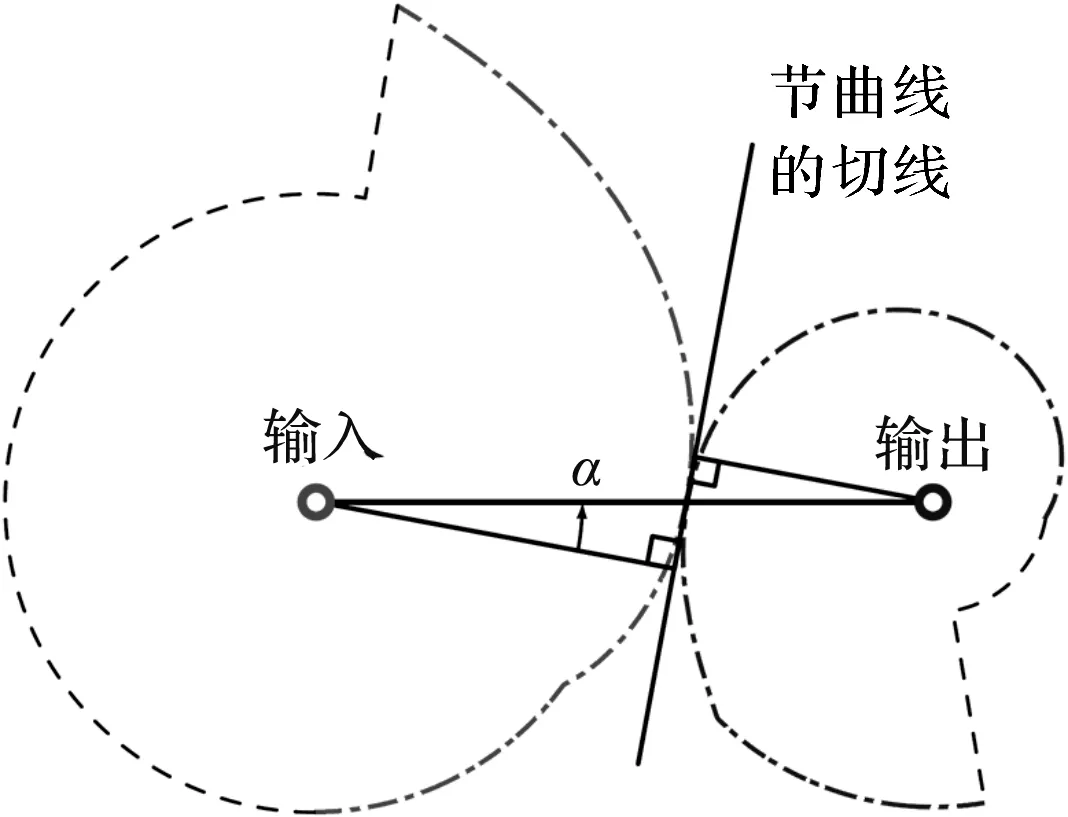
图9 压力角α的定义
输入和输出齿轮中心之间的距离为0.056 m。从图9可以看出,通过设置G2min为1,轮齿压力角的变化小于50°[14-16]。
2.3 与圆形齿轮的比较
为了说明异形齿轮的有效性,笔者计算了采用圆形齿轮的最佳恒定传动比。恒定传动比与跳跃高度的关系如图10所示。
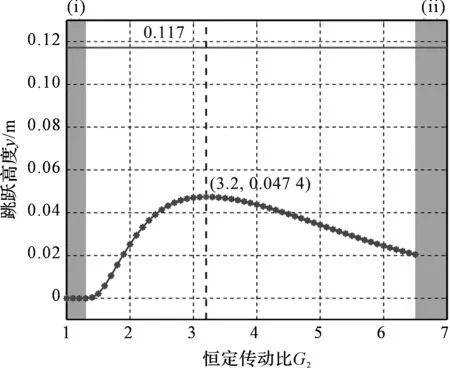
图10 恒定传动比与跳跃高度的关系
图10中,将G2设定为常量,通过仿真计算跳跃高度。在灰色区域(i)中,机器人由于传动比小(主体速度小)而无法跳跃;在区域(ii)中,机器人由于传动比大、扭矩小而不能站立。
可以看出:G2为3.2时机器人的最大跳跃高度为0.047 4 m,远小于使用异形齿轮时的跳跃高度(0.117 m,G2min为1)。
为了研究其原因,笔者对电机功率和功耗进行了计算。电机功率对比如图11所示。
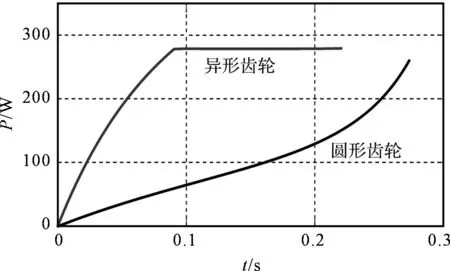
图11 电机功率对比
电机功对比如12所示。
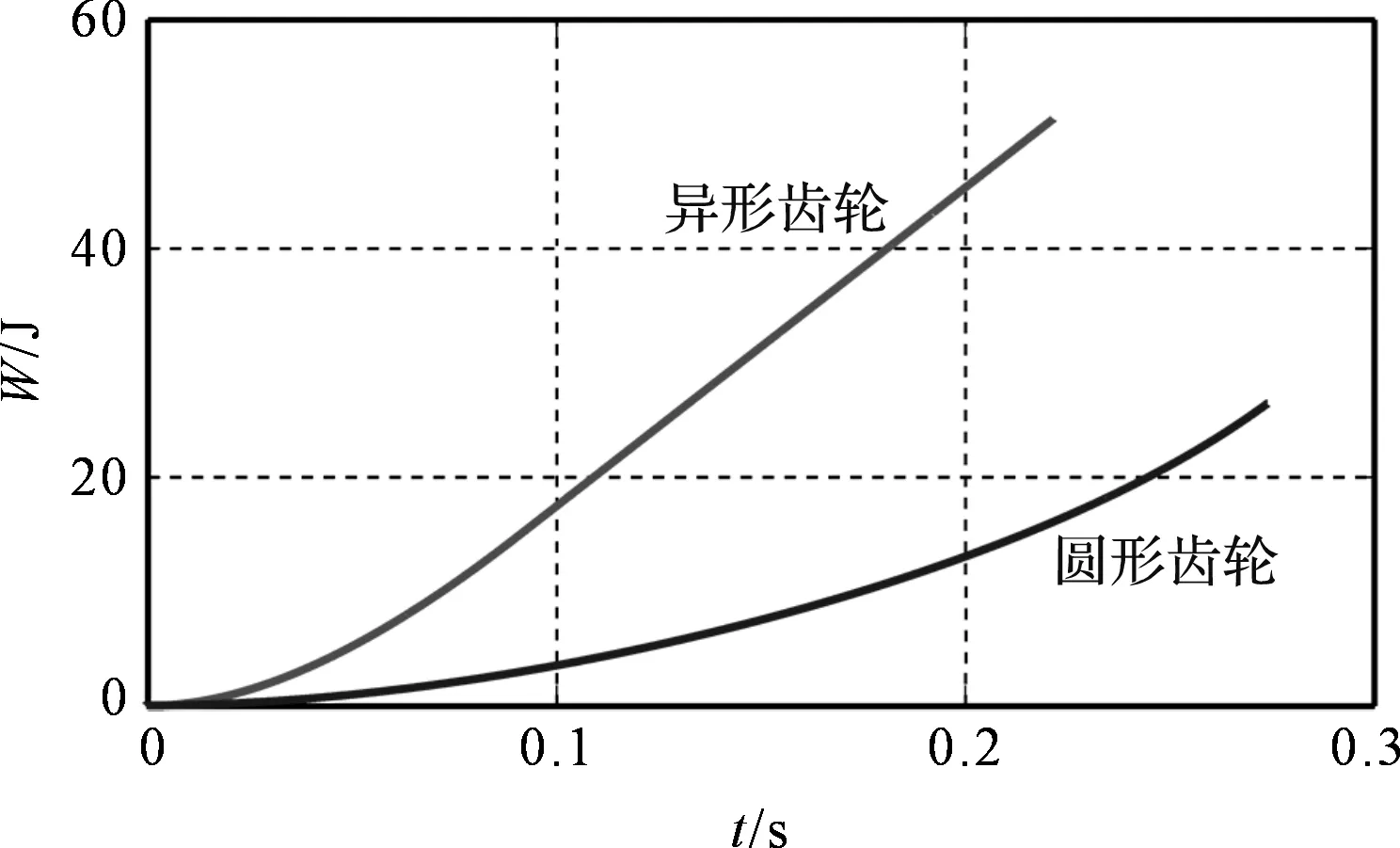
图12 电机功对比
2.4 跳跃高度对参数扰动的敏感性
图7中,异形齿轮是基于正向动力学分析为指定的机器人和指定的初始位置设计的(M为1.65 kg,φ10为10°),有必要评估跳跃高度相对于参数扰动的变化。因此,笔者根据重量扰动ΔM和角度扰动Δφ10计算了跳跃高度的变化。
相对于重量扰动的跳跃高度变化如图13所示。
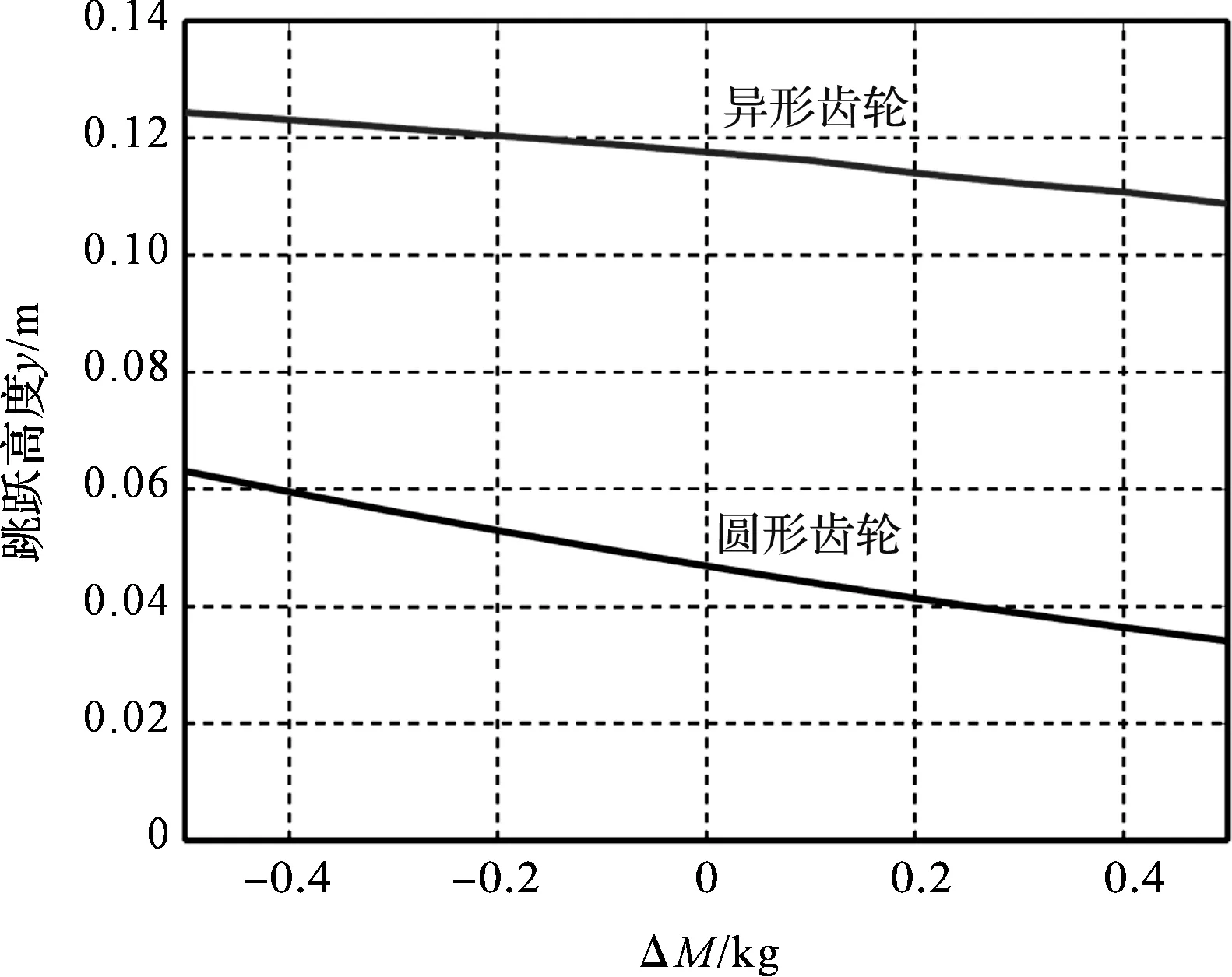
图13 相对于重量扰动的跳跃高度变化
相对于角度扰动的跳跃高度变化如图14所示。
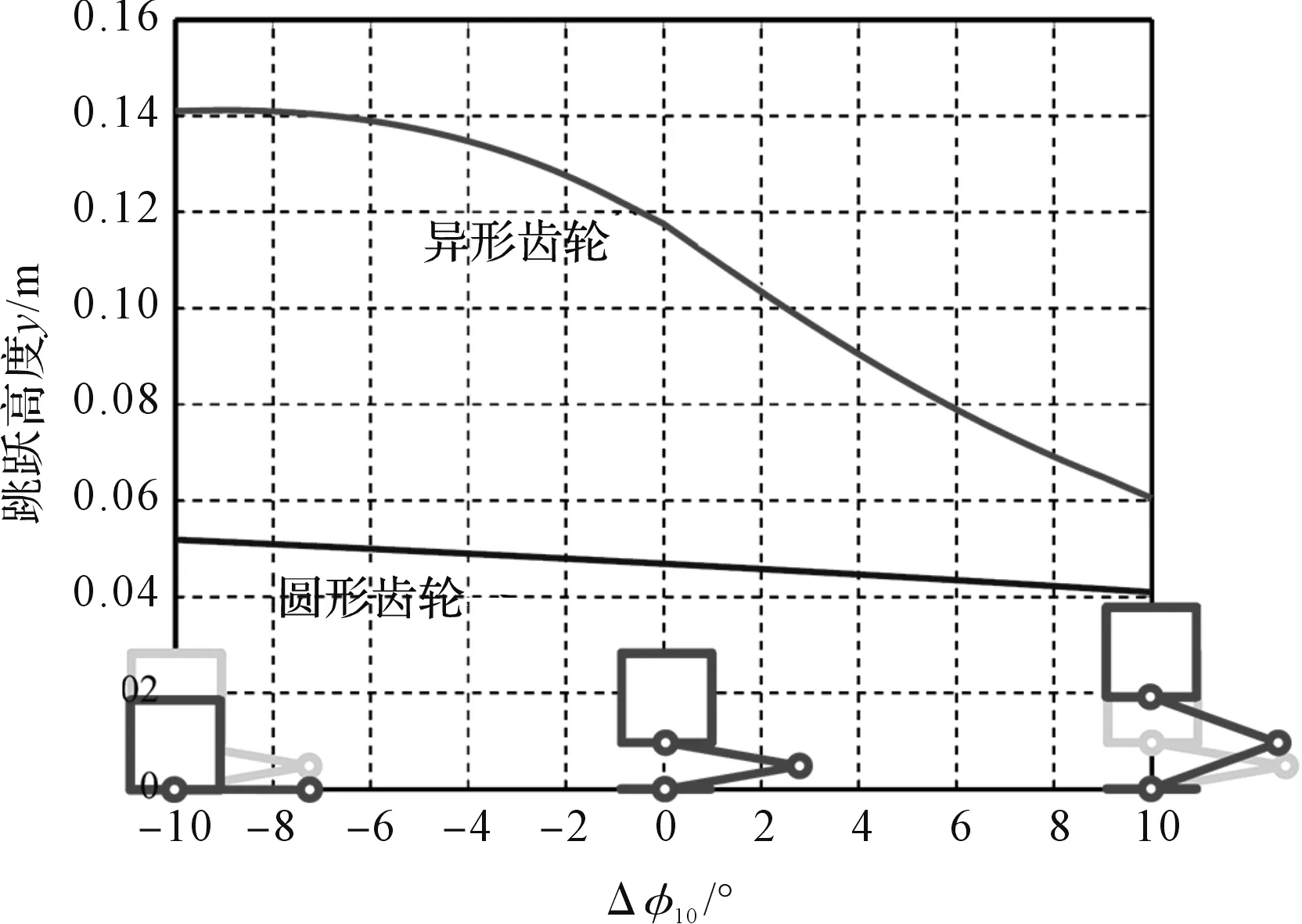
图14 相对于角度扰动的跳跃高度变化
从动力学的角度来看,不管使用圆形齿轮还是异形齿轮,即使是较轻的重量和较小的初始角度也会产生较高的跳跃高度。然而,在参数扰动的所有情况中,异形齿轮均获得了比圆形齿轮更高的跳跃高度。
3 实验结果与分析
3.1 原型机
笔者设计并制造了一个跳跃机构的原型,重量M为1.65 kg,l为0.15 m,G1为1/28,G3为1/5。采用了MAXON公司的4.90W-DC电机,其电阻R为2.07 Ω,扭矩常数Ka为52.5×10-3Nm/A,E为48 V,限流imax为12 A,φ10为10°。
跳跃机构的原型如图15所示。
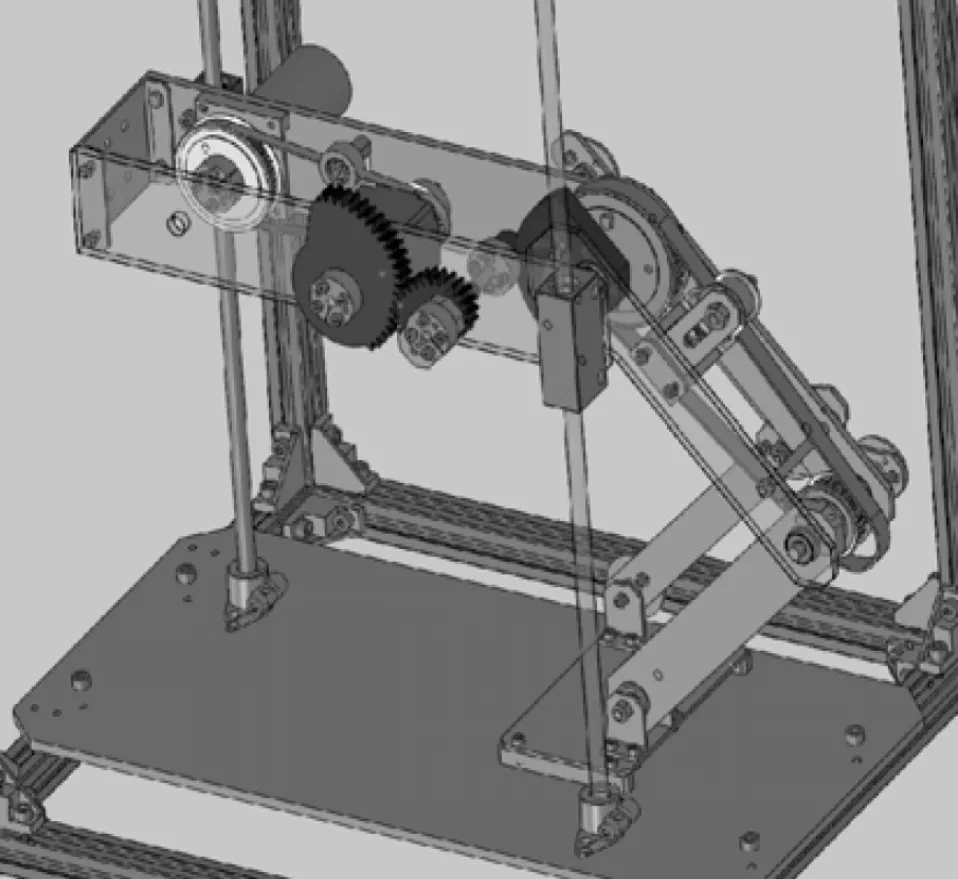
(a)三维CAD模型
根据图7中的节曲线,笔者制作了一个异形齿轮的原型。由于图7中的俯仰曲线有一个不可微分点,此处采用样条插值,以便获得光滑的曲线。
异形齿轮的厚度为10 mm,模数为1.5,制造材料为合金工具钢(SKD11)。异形齿轮的原型如图16所示。

图16 异形齿轮的原型
3.2 跳跃实验
笔者利用异形齿轮(G2min为1)和圆形齿轮进行了跳跃实验,跳跃实验结果对比如图17所示。

(a)异形齿轮,0.0 s
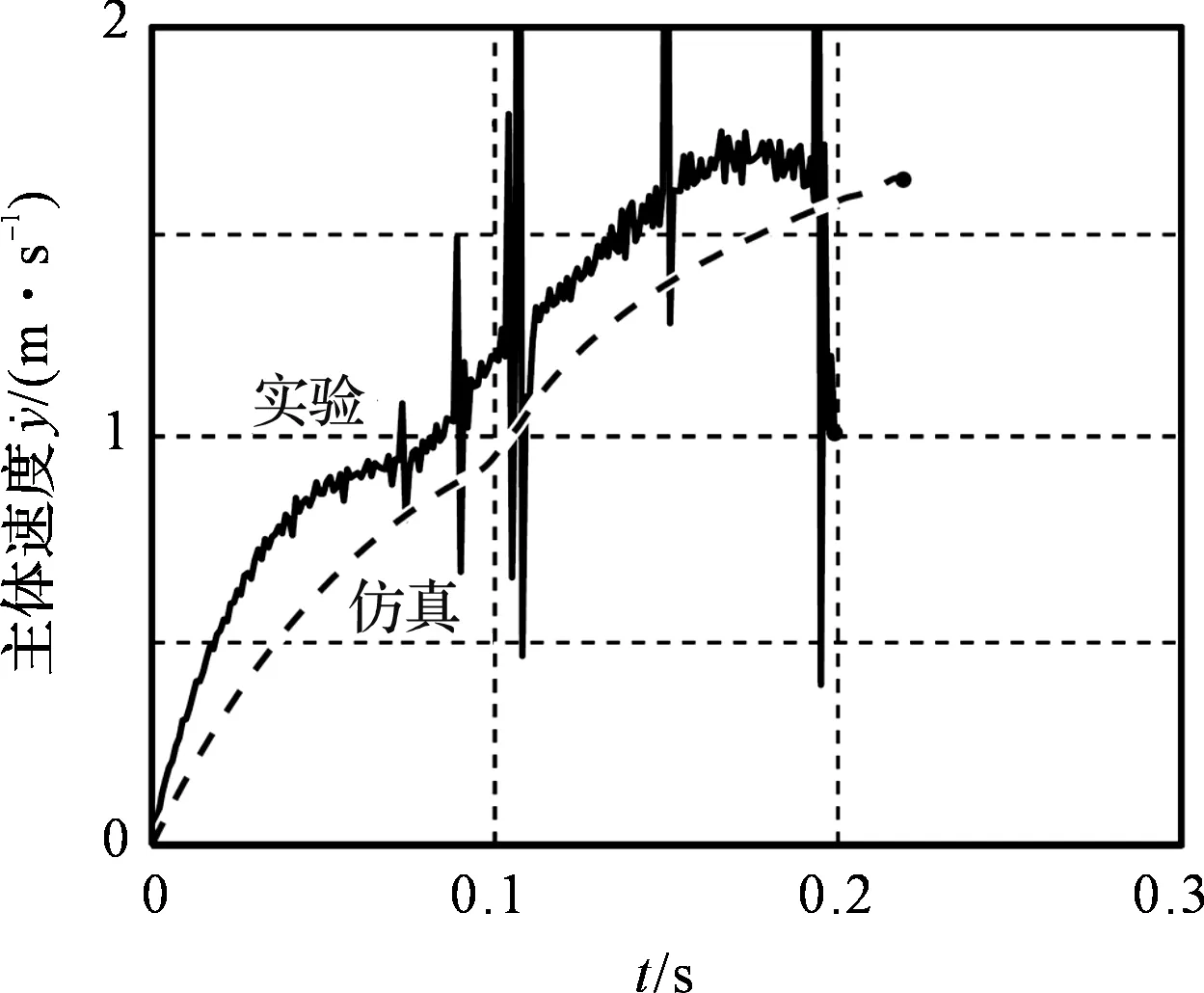
图18 实验和仿真的比较
相对于初始姿态扰动的跳跃高度变化如图19所示。

图19 相对于初始姿态扰动的跳跃高度变化
图19与仿真结果(图14)相同,采用异形齿轮时,在初始姿态扰动的所有情况中,其跳跃高度都大于圆形齿轮。
4 结束语
本文提出了一种适用于跳跃机构的齿轮最优变传动比设计方法,并采用异形齿轮对其进行了具体实现,有效地提高了电机效率;通过变传动比跳跃机构原型的实验测试,得出了如下结论:
(1)采用异形齿轮的跳跃高度为0.135 m,为圆形齿轮的1.68倍,说明采用异形齿轮的电机功率比采用圆形齿轮的电机功率要大得多;
(2)由于所提出的方法是基于正向动力学分析的,结果依赖于机器人物理参数的扰动。然而,在参数扰动的所有情况中,异形齿轮均获得了比圆形齿轮更高的跳跃高度。
在后续的研究中,笔者将在无支撑连杆条件下,对异形齿轮进行跳跃测试,以便针对其稳定性开展进一步的分析。

