不同剪跨比节能砌块隐形密框复合墙体恢复力模型
翁志雄, 李升才, 朱永甫
(1. 华侨大学 土木工程学院, 福建 厦门 361021; 2. 闽南理工学院 绿色建筑施工与管理福建省高校工程研究中心, 福建 泉州 362700)
节能砌块隐形密框复合墙体结构是一种新型的节能结构体系[1],具有消能减震、多线抗震、快速施工、节能环保等优点[2],能将建筑节能技术与现代建筑有效地结合起来.其中,节能砌块更是一种含结晶水的防火耐火材料,适用于需要高水平被动防火的墙壁.该结构采用配筋和截面较小的混凝土搭建起的肋格作为结构骨架[3],轻质隔板作为结构隔墙,形成具有密布隐形柱、梁、节能砌块及结构大框架共同受力的隐形密肋框架结构.
在国外,Alexander等[4]5片不同剪跨比的剪力墙进行拟静力试验,结果表明,随着墙体剪跨比的降低,墙体位移承载力降低.Barda[5]对8片带翼缘剪力墙进行抗震性能分析,得到当墙体的剪跨比从0.5增加到1.0时,墙体承载力降低了20%.在国内,蔡健等[6]通过对不同剪跨比的组合剪力墙进行抗震性能研究,得到随着墙体剪跨比的增大,墙体承载力降低,延性提高,耗能能力增强.然而,国内外学者对不同剪跨比的节能砌块隐形密框复合墙体抗震性能的研究较少[7-14].因此,本文通过对6片不同剪跨比的1/2缩尺试件进行水平低周往复加载试验,研究剪跨比对墙体抗震性能的影响,建立其恢复力模型.

表1 试件主要参数Tab.1 Main parameters of specimens
1 试验方案
1.1 试件设计与配筋
设计并制作了6片不同剪跨比的1/2比例缩尺节能砌块隐形密框复合墙体试件,试件主要参数,如表1所示.表1中:b,h分别为墙体的宽度和高度;λ为墙体剪跨比;fcu,k为砼标准试块抗压强度.各试件均由地梁、复合墙体、顶梁组成.6个试件的编号分别为CW-1~CW-6.以试件CW-2为例,试件几何尺寸及构造,如图 1所示.其他5片墙体的配筋情况与试件CW-2相同.

(a) 立面图 (b) 2-2剖面 (c) 1-1剖面图1 试件几何尺寸及构造(单位:mm) Fig.1 Dimensions and details of specimens (unit: mm)
1.2 材料的力学性能
试验采用的节能砌块长150 mm,宽110 mm,高150 mm;砌块两侧、上方分别留有直径60 mm的半圆形及60 mm×50 mm的矩形凹槽以便后续浇筑自密实混凝土.砌块的抗压强度为15.8 MPa,抗拉强度为1.66 MPa,干质量为10.15 kN· m-3,弹性模量为1.950 GPa. 试验浇筑所采用的混凝土均为设计强度等级C20的细石混凝土.密柱、密梁内各类钢筋的力学性能,如表2所示.表2中:d为钢筋直径;fy为屈服强度;fb为极限强度;Es为弹性模量.试件的制作过程大致如下:首先浇筑试件基础;之后,逐层砌筑相应数量的节能砌块,在砌筑墙体过程中,在砌块预留凹槽处分别放置对应型号钢筋并浇筑自密实流动混凝土砂浆以形成密梁密柱;最后,绑扎顶梁钢筋笼并浇筑完成整个试件.相较于其他复合墙,节能砌块隐形密框复合墙的制作过程简单,较大程度地节省了劳动成本及制作时间,适合运用到实际工程中.
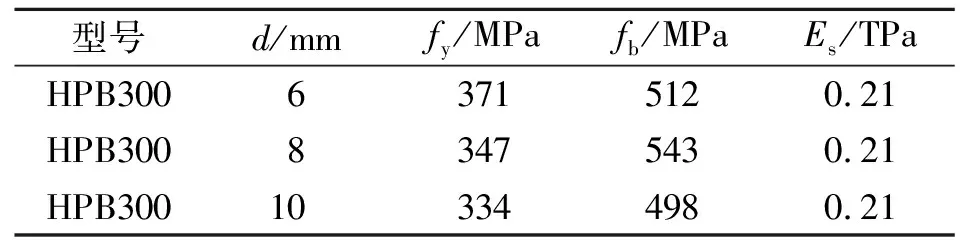
表2 钢筋的力学性能Tab.2 Mechanical properties of steel reinforcement

图2 加载及测量装置(单位:mm) Fig.2 Loading and measuring device (unit: mm)
1.3 试验加载方案
试验在华侨大学抗震实验室进行,采用MTS加载装置进行加载控制.加载方式为由位移控制的水平低周反复加载,即试件竖向不施加荷载,顶梁梁端施加作用于中心点的水平反复荷载.数据采集系统主要由应变片、物理位移计、激光位移计组成,加载及测量装置,如图2所示.
在试件屈服前,每级位移循环一次;当墙体荷载-位移(P-Δ)曲线出现拐点时,说明墙体屈服,在试件屈服后每级位移循环两次.试件加载过程中,如果顶梁水平荷载降低至极限荷载的85%以下或墙体发生严重变形时,停止加载.加载制度,如图3所示.图3中:n为循环次数.

(a) 试件CW-1 (b) 试件CW-2 (c) 试件CW-3

(d) 试件CW-4 (e) 试件CW-5 (f) 试件CW-6图3 加载制度 Fig.3 Loading pattern
2 试验结果与分析
2.1 试件破坏结果
试件CW-1裂缝密集,在节能砌块和墙体的主对角线上出现明显的斜裂缝,整个墙体的裂缝大致呈X形分布.整个墙体的破坏过程剪压现象明显,属于剪压破坏.试件CW-2的裂缝扩展形式与试件CW-1相类似;试件CW-3的裂缝主要分布在墙体对角线上,裂缝类型主要为斜裂缝,但还没有形成与试件CW-1相似的裂缝带;试件CW-4的裂缝主要集中分布在墙体形心处,裂缝类型以弧形斜裂缝为主;试件CW-5的裂缝主要分布在墙体的上端和下端,裂缝类型复杂,主要以斜裂缝为主,以及少量的弧形和水平裂缝,由此可知,该试件的破坏类型属于弯剪破坏;试件CW-6的裂缝相较于试件CW-5分布更广,复合墙两侧和中间砌块均出现水平裂缝.试件最终破坏状态,如图4所示.
经比较分析不难看出,随着墙体剪跨比的增大,墙体破坏现象逐渐由剪切破坏转为弯剪破坏.具体为当墙体剪跨比λ<1.50时,墙体的破坏现象主要为剪切破坏;但λ≥1.50时,墙体的破坏现象主要为弯曲破坏.由此可见,剪跨比对试件破坏现象的影响较小.

(a) 试件CW-1 (b) 试件CW-2 (c) 试件CW-3

(d) 试件CW-4 (e) 试件CW-5 (f) 试件CW-6图4 试件破坏状态 Fig.4 Failure modes of specimens

(a) 试件CW-1 (b) 试件CW-2 (c) 试件CW-3

(d) 试件CW-4 (e) 试件CW-5 (f) 试件CW-6图5 P-Δ滞回曲线 Fig.5 P-Δ hysteretic curves
2.2 试件滞回特性
通过对试验数据的整理,绘制6个试件的P-Δ滞回曲线,如图5所示.由图5可知:6片墙体的滞回曲线都较为饱满,滞回环都主要呈现反S型,墙体抗震性能较好.在墙体开裂之前水平荷载较小,试件处于弹性阶段,滞回曲线接近直线且所包围的面积较小,试件加载、卸载曲线接近重合.随着水平荷载不断加大,墙体开裂,滞回曲线开始由直线转为曲线,滞回环包围面积逐渐增大,试件开始出现加载刚度及卸载刚度退化.滞回曲线逐渐“捏拢”,这时滞回曲线虽然靠近轴线,但整体滞回面积较大,复合墙体延性、塑性较好,具有较好的耗能能力.
由图5还可知:当试件剪跨逐渐增大时,试件初始刚度减小,墙体耗能能力提高,承载能力降低.当1.00≤λ≤1.80时,通过分析对比试件CW-3~CW-6可知,试件加载、卸载刚度退化减缓,极限变形能力提高,符合抗震性能要求.
2.3 骨架曲线
各试件的骨架曲线特征点试验结果与计算结果的比较,如表3所示.表3中:以第一次出现裂缝的点为开裂点;屈服点由等效能量法计算得出;峰值荷载点为构件所能承受荷载的最大值;Pc,Py,Pu分别为开裂荷载、屈服荷载和破坏荷载;Δc,Δy,Δu分别为试件加载到开裂荷载、屈服荷载和破坏荷载时的位移值;Pm为试件承受的最大荷载;Δm为试件达到最大荷载时的位移值;μ为延性系数.
由表3可知:随着剪跨比的增大,试件的峰值荷载减小,但破坏时位移增大;当λ≤1.00时,对比试件CW-1,CW-2,CW-3,随着剪跨比从0.50增大到1.00,承载力下降了51.50%,位移延性系数从2.30增加到3.47,增加了50.87%;当λ>1.00时,对比试件CW-4,CW-5,CW-6,随着剪跨比从1.28增大到1.80,承载力下降了27.65%,位移延性系数从3.78增加到4.46,增加了17.99%.

表3 骨架曲线特征点试验结果与计算结果的比较Tab.3 Comparison of test results and calculation results of skeleton curves at characteristic points

图6 试件的荷载-位移骨架曲线 Fig.6 Load-displacement skeleton curves of specimens
各试件的荷载-位移骨架曲线,如图6所示.由图6可以看出:墙体的受力阶段大致分为弹性、弹塑性、破坏3个阶段.相比于其他试件,试件CW-1在弹性阶段初始刚度和承载力最大;当试件达到极限承载力后,曲线下降较快,变形能力较差.相较于试件CW-1,试件 CW-2的初始刚度和极限承载能力降低,但试件延性增大,变形能力提高;试件CW-3,CW-4,CW-5,CW-6的骨架曲线不论弹性阶段还是弹塑性阶段变化都接近相同,延性逐渐提高,总体变化相差不大.
综上可知,随着墙体剪跨比的增大,墙体初始刚度及承载力随之减小,墙体延性和变形能力提高.
2.4 刚度退化
刚度大小能在一定程度上反映墙体的耗能能力.随着刚度增大,墙体耗能能力减小.所以,结构刚度需要合理设计,才能让结构有较好的抗震性能.在对6个试件的试验过程中,随着水平力的不断增大,墙体首先开裂破坏,导致试件整体刚度下降,刚度退化现象随之发生.为探究墙体的刚度退化规律,试件的割线刚度Ki表达式为
(1)
式(1)中:Ki为第i次循环的割线刚度平均值;Pi1为第i次循环反向加载的水平峰值荷载;Pi2为第i次循环正向加载的水平峰值荷载;Δi1为第i次循环反向加载水平峰值荷载对应的位移;Δi2为第i次循环正向加载水平峰值荷载对应的位移.
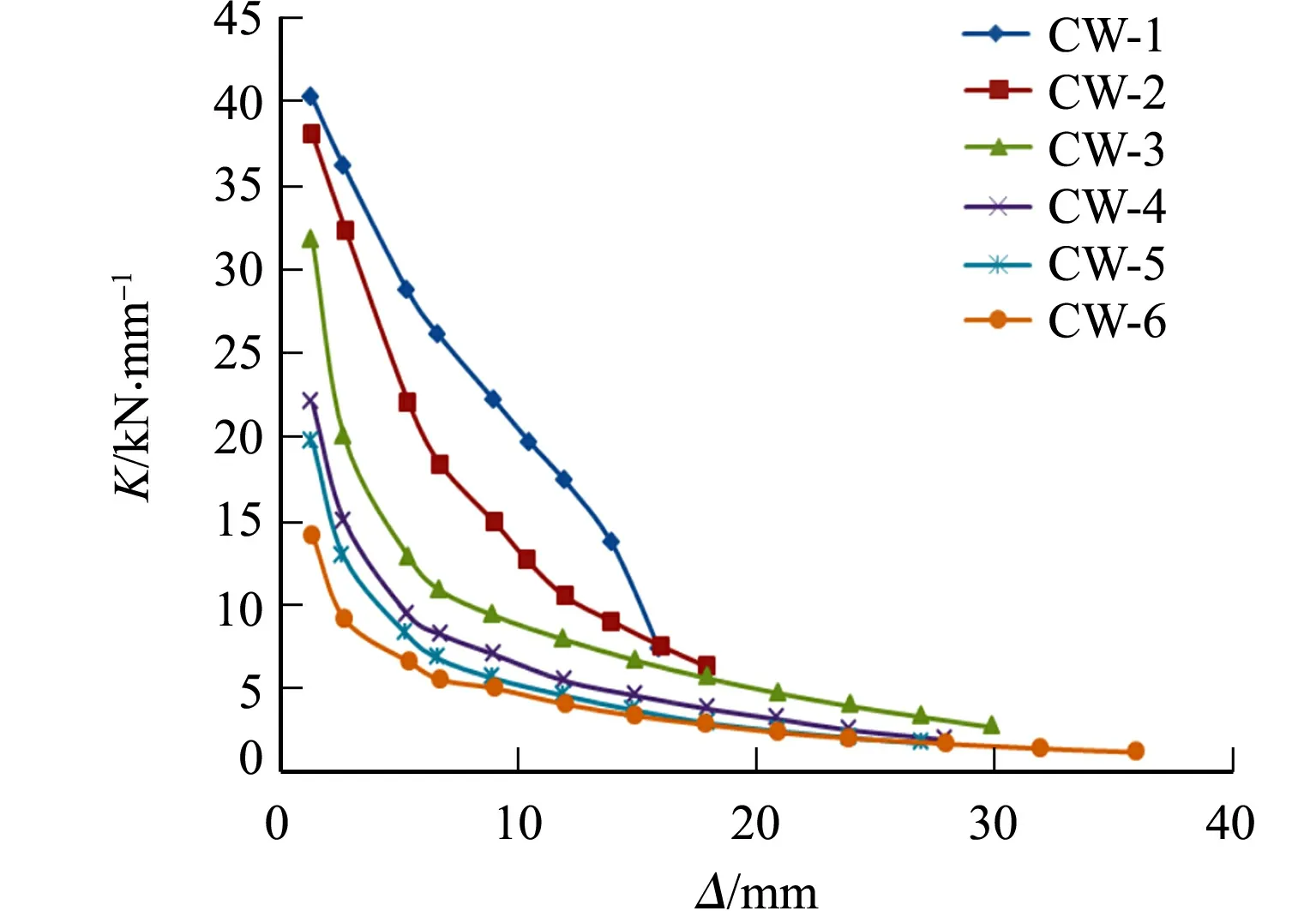
图7 刚度退化曲线 Fig.7 Stiffness degradation curve
由上述刚度定义公式,分别计算各试件的平均割线刚度,绘出各试件的刚度退化曲线,如图7所示.图7中:K为割线刚度.由图7可知:试件CW-1初始刚度最大,在刚度退化的前期和后期速率都较快.试件CW-2,CW-3的初始刚度较大,前期退化速率较快,曲线相对较陡.试件CW-4,CW-5,CW-6的初始刚度较小,前期退化速率较慢,后期刚度退化均同步趋于平缓.由此可见,剪跨比越大的试件,初始刚度越大,前期刚度退化速率越快.而后期因试件变形增大刚度退化速率逐渐平缓,当剪跨比λ>1.00时,曲线平缓且接近重合,墙体剪跨比对刚度退化的影响逐渐减小.
3 不同剪跨比复合墙体的恢复力模型
3.1 骨架曲线及滞回规则
通过对6个不同剪跨比的节能砌块复合墙体试验现象、滞回特性、骨架曲线和刚度退化现象等抗震性能指标的研究,提出四折线骨架模型,如图8所示.定义第1个拐点A为试件开裂点;B为试件屈服点;C为试件峰值荷载点;D为试件破坏点.

图8 恢复力模型 Fig.8 Restoring force model
通过节能砌块复合墙体的滞回特征分析,得到其滞回规则如下.
1) 当试件由图中点O加载至点A,OA段刚度为弹性刚度,即K0;当试件继续加载至点B,则定义AB段刚度为屈服前刚度,即K1;第2循环BC段刚度为K2;第3循环CD段刚度为K3.
2) 试件滞回规则按第1循环0-1-2-6-10-11-15-2,第2循环2-3-7-11-12-16-3,第3循环3-4-8-12-13-17-4,第4循环4-5-9-13-14-18-5的顺序加载及卸载循环.
四线型各阶段刚度K0,K1,K2,K3的计算公式分别为
(2)
(3)
(4)
(5)
计算6个试件的割线刚度,如表4所示.

表4 恢复力模型各阶段刚度Tab.4 Stiffness at each stage of restoring force model

图9 不同阶段卸载刚度 Fig.9 Unloading stiffness at different stages
3.2 卸载刚度
卸载刚度指各试件骨架曲线上的卸载点与原点O连接直线的斜率,从6个试件所形成的滞回曲线不难看出,试件在加载过程和卸载过程的刚度都会有退化的现象.考虑到工程应用及计算方便,此处四线恢复力模型刚度退化规律可分为3个阶段:第1阶段为试件达到屈服荷载对应的位移;第2阶段为试件达到最大荷载对应的位移;第3阶段为试件达到极限荷载对应的位移.不同阶段的卸载刚度,如图9所示.
分别对试件在屈服点、峰值荷载点、破坏点3个阶段卸载刚度的计算结果进行统计并回归分析,通过插值可得各阶段卸载刚度Kr,i和初始刚度K0关系为
Kr,1=(Δc/Δr)0.5·K0,Δc<|Δr|≤Δy,
(6)
Kr,2=(Δy/Δr)0.61·K0,Δy<|Δr|≤Δm,
(7)
Kr,3=(Δm/Δr)0.63·K0,Δm<|Δr|≤Δu.
(8)
式(6)~(8)中:Δr为墙体卸载时的位移.
3.3 骨架曲线的拟合
为了验证文中建议的四线恢复力模型,根据推导的计算方法分别计算出6个节能砌块复合墙体的骨架曲线,再将计算曲线与试验实测曲线进行比较,如图10所示.由图10可知:在整个受力过程中,复合墙体计算所得的骨架曲线与试验所得骨架曲线吻合度较高,能够较好地反映不同剪跨比节能砌块复合墙体的滞回性能及荷载-位移关系.
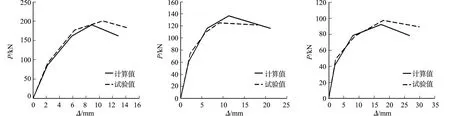
(a) 试件CW-1 (b) 试件CW-2 (c) 试件CW-3

(d) 试件CW-4 (e) 试件CW-5 (f) 试件CW-6图10 计算与试验骨架曲线的对比 Fig.10 Comparison of calculation and test skeleton curves
4 结论
1) 在水平荷载作用下,所研究的不同剪跨比复合墙体一般会出现剪切破坏的现象,破坏过程可大致分为弹性、弹塑性和破坏3个阶段.当剪跨比λ<1.50时,墙体的破坏形式以剪切破坏为主;当剪跨比1.50≤λ<2.00时,墙体的破坏形式以弯曲破坏为主.由砌块、内密肋框架共同构成了抵抗墙体破坏的两道防线,说明文中所研究的复合墙体相较于普通墙体有更好的抗震性能.
2) 剪跨比是影响墙体承载力退化的主要因素,剪跨比越大,墙体的承载力退化越快.当剪跨比λ>1.50时,墙体剪跨比对其承载力的影响有所减小,但对墙体的耗能与延性的影响较大.与普通墙体相比,所研究的节能砌块隐形密框复合墙体的延性、耗能能力较好.在建立恢复力模型时,应考虑剪跨比对试件承载力及刚度退化的影响.
3) 通过分析复合墙体在往复荷载作用下的试验数据及荷载-位移滞回曲线特征,得到不同剪跨比节能砌块隐形密框复合墙的承载力退化规律,并建立相关计算式.确定不同剪跨比节能砌块隐形密框复合墙恢复力模型滞回规则,从而建立考虑剪跨比对滞回特性影响的复合墙体P-Δ曲线的恢复力模型.
4) 将计算与试验所得的骨架曲线进行对比可知,采用文中建议的不同剪跨比节能砌块隐形密框复合墙体恢复力模型能较好地反映不同剪跨比对复合墙体滞回特性的影响,为理论分析和实际工程设计提供了一定参考.

