地铁站台火灾顶棚烟温的分布特征与预测

张迎新， 武 璇， 李日军

(黑龙江科技大学 安全工程学院， 哈尔滨 150022)

0 引 言

地铁是现代城市中人们出行迅捷的交通工具，因地铁站处于受限空间环境，通风和疏散不便，一旦发生火灾易造成重大事故，给社会经济带来巨大损失[1]。2003年，大邱地铁火灾分别造成死亡198人，伤147人；2017年，香港地铁尖沙咀站发生火灾，致18人受伤[2]。据报道，火灾事件中大约80%的受害者死于有毒的热烟，烟雾和高温是火灾发生时不可避免的两种危害。为此，研究人员针对站台火灾展开广泛研究。陈俊沣等[3]釆用1∶10的实验模型，研究了车站内站厅及站台危险位置发生火灾时的优化排烟方案。张雷等[4]用FDS分析了喷淋和排烟系统作用下地铁站台的火灾烟气流动和排烟控制。Cong等[5]通过实验和仿真研究了列车火灾位置对地铁隧道顶下最大烟气温度的影响。Chen等[6]建立了不同密封比下隧道洞口顶下气体温度的变化和修正模型。陈奕岑[7]等用FDS模拟了地铁枢纽站换乘口火灾,并在Alpert公式基础上,提出了一种包含弗劳德数和经验常数的预测公式。结果表明,该公式相比于已有的经验公式有着更高的预测准确度。钟委等[8]通过室内实验研究了水平雾幕对地铁车站顶棚射流火焰、烟气沉降抑制的作用效果。结果表明，施加水平雾幕对顶棚射流火焰具有显著的抑制作用，烟气出现分层现象,且烟气最高温度、烟气出口速度均小于施加竖向雾幕。Zhang等[9]在1∶10模型中进行了不同放热率、纵向通风速度和火源间距的实验，考虑双火源条件下的顶棚最高温度。Liu等[10]通过全尺寸实验模拟研究了站内顶棚温度和烟气层厚度。

上述研究成果大多针对隧道和站台火灾顶棚最高和垂直温度建立了预测模型，对地铁火灾机理和发展规律起到了良好的推进作用。由于站台火灾存在复杂性和紧迫性的特点，火灾位置和站台形状导致站台烟气层的下降和断面温度场的不均匀，Alpert和Ji的经典型对温度的预测结果存在偏差。因此，基于火灾位置(站台端部、楼梯背端、楼梯口处和站台中部)和火源功率的站台顶棚纵向温度的预测，其结果会更加准确、适用性更广。由此，笔者利用Froude相似准则建立了1∶10小尺寸火灾实验，共设置8种工况下的站台火灾，同时采用Pyrosim建立了地铁小尺寸模型数值模拟，将实验与模拟数据比较，吻合良好，以此证明模拟的有效性。同时，建立了全尺寸站台数值模型，针对4种不同火源位置、4种不同火源功率的16种工况进行数值模拟，分析了随纵向距离变化站台顶棚下烟温的分布规律，得到了纵向分布无量纲峰值温度(ΔTmax,D)/ΔTmax)的预测公式。这些研究为人员逃生提供条件，对地铁火灾时烟气的控制和高温预防具有实际意义。

1 小尺寸火灾实验

1.1 相似性准则

地铁站台火灾小尺寸实验主要采用Froude相似准则。由于火灾烟气羽流在狭长空间流动过程中主要受惯性力和浮力作用，因此，在用Froude模拟方法进行模拟时，必须保证模型和原型的Froude数相等[2，6]。在常压环境下进行的火灾模拟实验，烟气主要受浮力驱动。因此，首先要保证模型实验中无量纲数不变[9]，即：

(1)

考虑Froude数守恒，建立了缩尺模型与全尺模型的时间t，几何尺寸x、火源强度Q、烟雾温度T之间的相似关系。

时间：

(2)

几何尺寸：

(3)

火源强度：

(4)

温度：

TM=TF

，

(5)

式中：g——重力加速度；

v——特征速度;

l——特征长度;

F、M——全尺度参数和模型尺度参数。

1.2 实验设置

根据Froude相似准则，采用1∶10比例建立部分缩尺寸地铁站台模型。由于模型长度过长，且站台为对称几何结构，仅考虑火源位于站台左侧的情况，只建立左半部分模型。实验设计中模型尺寸为7 000 mm×1 100 mm×600 mm，如图1所示。为便于观察烟气发展传播规律，实验台采用防火玻璃制作，实验台左端封闭，右端上半部分敞开，来模拟站台端部火灾，两端敞开模拟站台中部火灾。

为监测火灾时站台模型空间内的温度场分布，对实验系统进行热电偶布置，共布置热电偶19个，水平布置13个，布置高度距顶棚10 mm，间距500 mm。每个火源点处垂直布置3个，间距100 mm。用于监测站台火灾时空间温度分布情况，如图1所示。

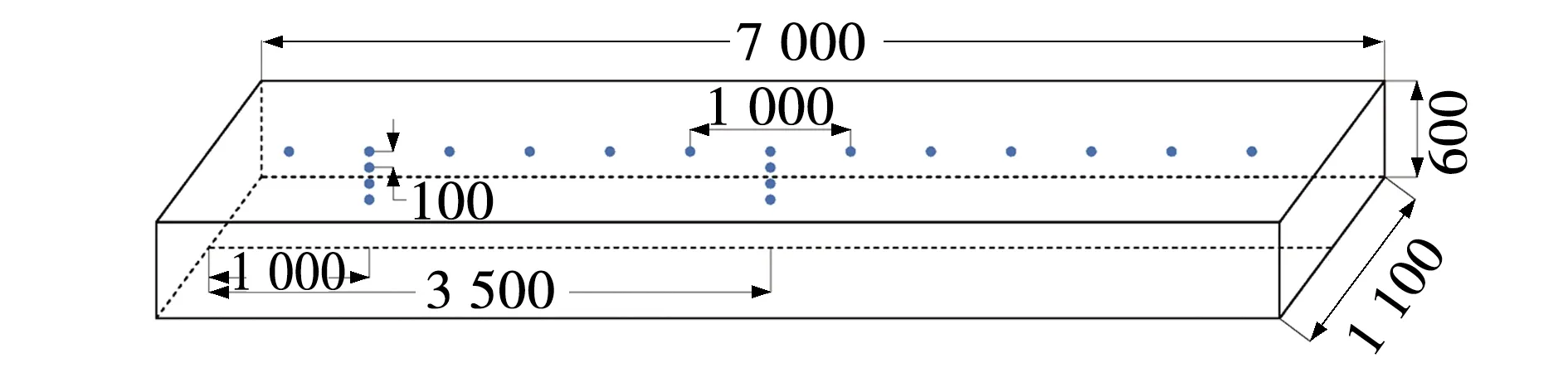
图1 缩尺寸地铁站台模型Fig. 1 A miniaturized model of a subway platform

实验中采用超快速火——池火，采用柴油作为火源。实验设计了半径为8、9、10、11 cm，高度50 mm的圆形油盘。油盘是用2 mm厚的钢板制成的。热释放率为

ΔH——柴油燃烧热，取42 MJ/kg；

χ——燃烧效率，取0.8 m。

根据英国Building Research Establish报告中统计人员聚集公共场所火灾规模为2.0～2.5 MW，换乘站人员流动量大，大部分乘客携带行李等可燃物，考虑到人为纵火及其他爆炸物等，选取热释放功率Q为2.0～5.0 MW的火源[10]。通过相似性计算，对应模型火源功率Qt约分别为6.32、9.49、12.65、15.81 kW。火源位置采用端部和中部火灾，具有代表性，实验时间为180 s。对8种火工况站台火灾进行小尺寸实验，分析实验结果。设置实验工况如表1所示。

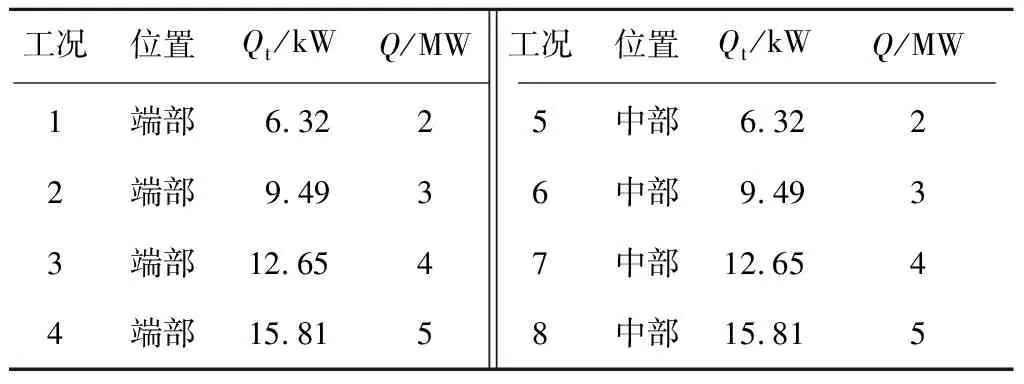
表1 小尺寸实验工况设置

1.3 结果分析

为了研究距火源距离对纵向烟温的影响，绘制了不同火灾位置(端部、中部)下顶棚纵 向温度的变化曲线，如图2所示。图中横坐标D表示从监测点到火源的距离。如图2a所示，火源位于端部时，顶棚温度随着与火源距离的增加，温度增长逐渐降低，最高温度出现在火源正上方。如图2b所示，火源位于中部时，顶棚纵向烟温分布呈对称性，由于本实验考虑了良好的通风条件，可以认为纵向天花板温度分布是对称的。端部火灾顶棚最高温度高于中部火灾28～39 ℃，这是由于火灾位于端部时没有位于中部时通风好。

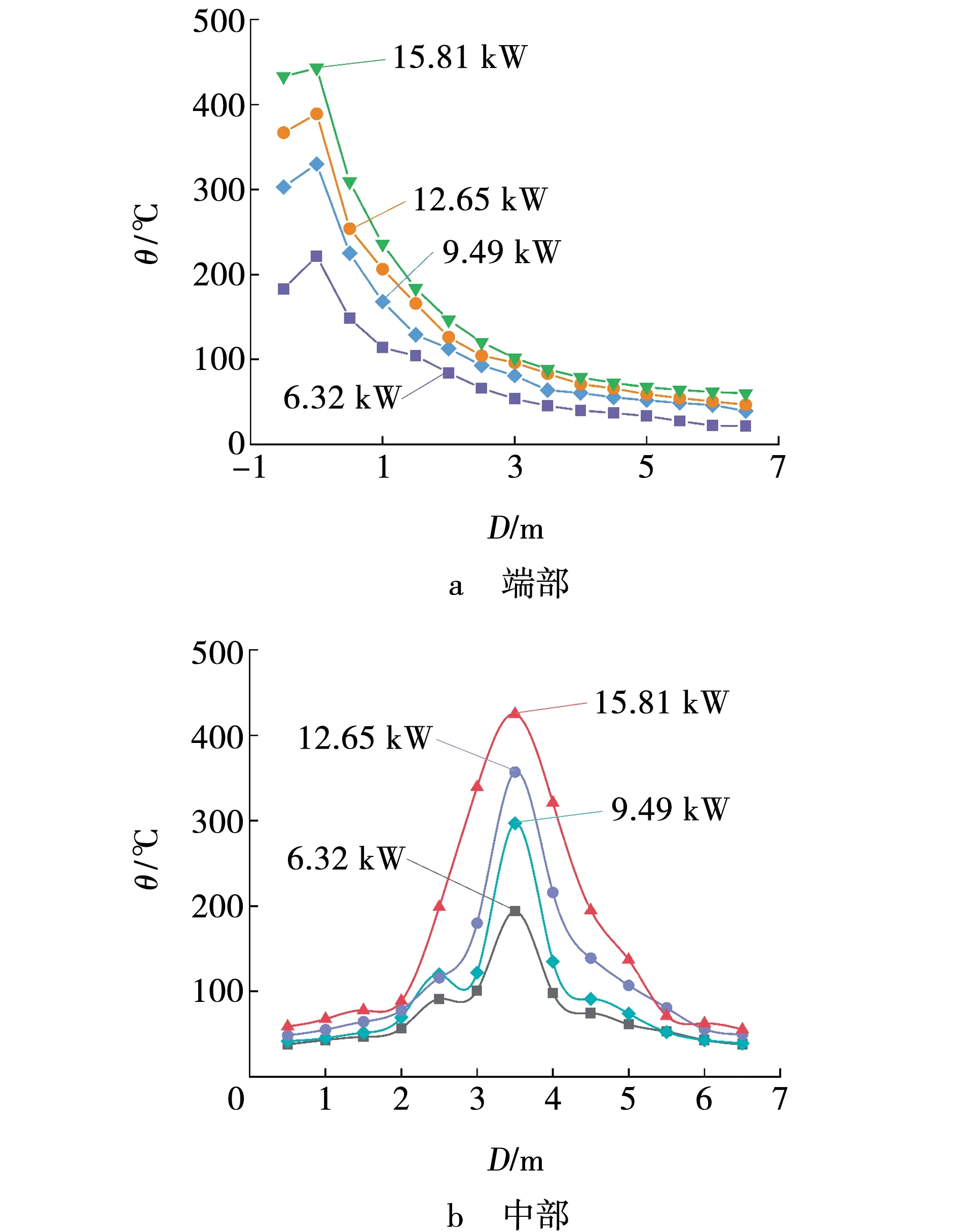
图2 火灾纵向温度分布Fig. 2 Longitudinal fire temperature distribution of fire

图3为中部火源正上方顶棚的温度随时间的变化，4种不同火源功率下，火源正上方顶棚温度0 ～ 10 s内迅速上升至最高温度，分别为185.6、304.1、368.6、480.7 ℃，10 s后温度趋于平稳，并且随着火源强度的增大，顶棚最高温度越高，烟气纵向流动速率越快。根据小尺寸火灾端部的温度测试，火源附近的烟雾有稳定的分层。不同火源功率下，端部4个垂直热电偶温度如图4所示。可以看出，离火源越近温度越高。由于较低的热电偶直接受到火焰的影响，所以在较低的点测得的温度要高于顶棚温度。中间高度的温度梯度变化较大，这是由于距离火源的距离以及烟障对烟气的阻隔作用造成的。

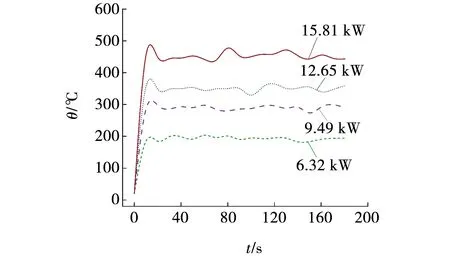
图3 中部火灾顶棚温度随时间变化Fig. 3 change of temperature of central fire ceiling with time

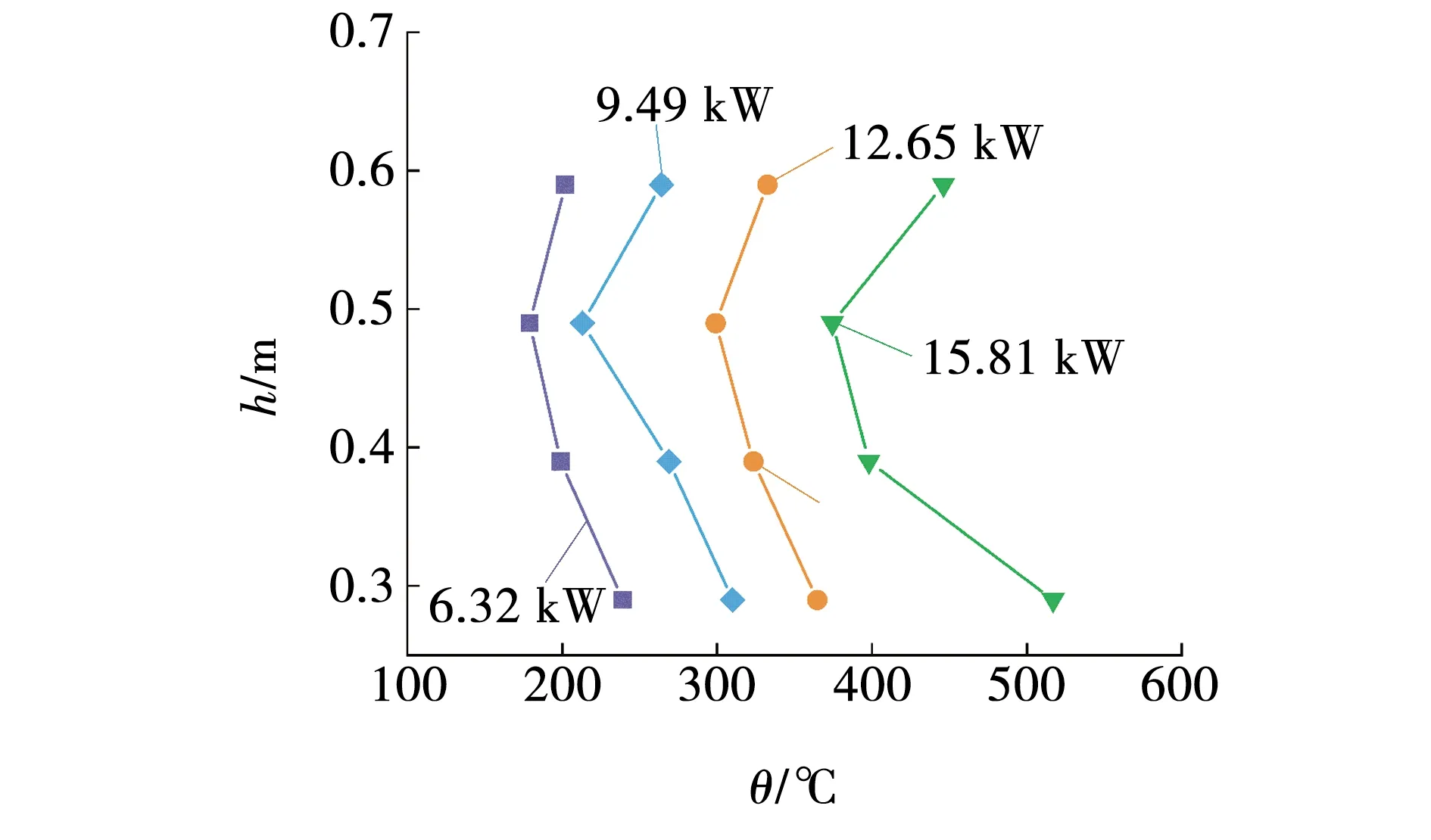
图4 不同火源功率下端部火灾垂直温度分布Fig. 4 Vertical temperature distribution of left fire under different fire tower

2 FDS数值模拟验证

2.1 参数设置

FDS采用大涡模拟(LES)技术，部分计算采用傅里叶变换(FFTs)的泊松求解器，一般采用均匀网格，网格方案对数值模拟结果有着决定性作用，网格的范围确定了计算区域，。网格尺寸在应用中为特征火焰直径的1/8～1/12，特征火焰直径D*采用式(6)计算[11]，即

(6)

ρ∞——空气密度，取1.2 kg/m3；

CP——空气比热，取1 kJ/(kg· K)；

T∞——环境空气温度，取293 K；

g——重力加速度，取9.81 m/s2。

在应用中网格尺寸通常取D*的1/10，可接受的网格大小是由火源功率决定的[12]。小尺寸模型中，火源功率为6.32～15.81 kW时，特征火焰直径为0.126 ～ 0.183 m，网格尺寸为0.01 ～ 0.02 m，结果差异不显著，网格越小计算时间大幅增加，因此，选取网格尺寸为0.02 m。尺寸模型中，火源功率为2.0～4.0 MW时，特征火焰直径为0.125～ 0.250 m，选取网格尺寸为0.20 m。

地铁模型的顶棚、侧壁、底板设置为1.0 m厚混凝土材料，火源是通过将燃料的物理参数设置到FDS中来确定的，能够最大限度地自由燃烧，这种设计方法比采用等放热率的设计火更接近实际火灾。火源的燃烧面积和测温点的布置可以通过参数直接设置。两个楼梯口均在无初始风速的情况下开启，属于自然通风条件。环境温度为293 K，环境压力为101.32 kPa。

2.2 小尺寸模型模拟验证

FDS在地铁火灾环境数值模拟中的可行性已有实验和理论广泛验证。建立1∶10实验设计相对应的数值模型。该模型与小尺寸实验台尺寸、火源位置、工况设置与监测点一致。监测纵向顶棚温度和火源点处垂直温度的变化，将数值模拟结果与实验结果进行对比，如图5、6所示，端部和中部火灾烟气温度与实验数据吻合较好，证明了FDS全尺寸地铁站台火灾数值模拟的正确性和可靠性[13]。

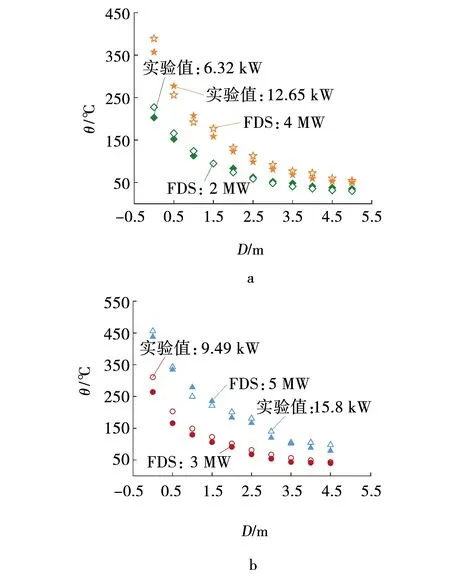
图5 端部火灾仿真与实验结果的比较Fig. 5 Comparison of left fire simulation and experimental results

纵向顶棚温度仿真与模拟结果如图5、6所示。当火源距离为0 ～1 m时，端部火灾位于一端封闭处，烟气累积导致温度偏高，中部火灾两侧通风，最高温度比端部火灾低26.8 ～ 52.4℃。在火源距离大于1 m时，主要由于热辐射导致温度升高，烟气层处于稳定阶段，误差小于7.2%。端部及中部的温度误差均小于10%，在允许的误差范围内，故认为所采用的数值模拟的方法是适用的。

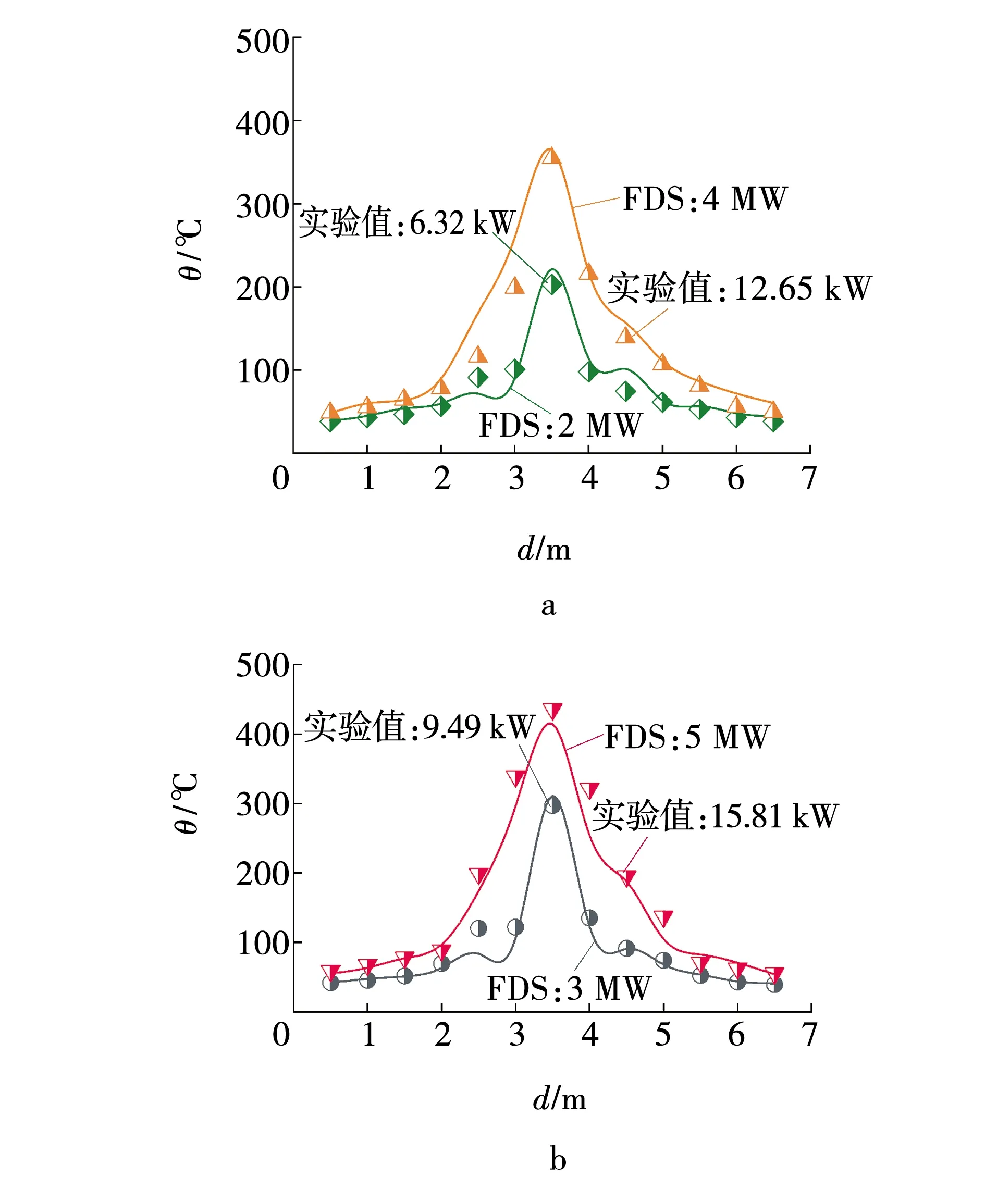
图6 中部火灾仿真与实验结果的比较Fig. 6 Comparison of simulation and experimental results of fire in central area

3 全尺寸数值模拟结果分析

3.1 数值模拟设置

根据地铁站台原尺寸建立数值模型，车站主建筑面积114 15.94 m2。站台公共面积1 424 m2，计算长度140 m，宽11 m，屏蔽门沿线路方向长度135.68 m。站厅公共区域面积为1 311 m2，长110 m，两端各设有楼扶梯一组，楼扶梯一侧设有防火卷帘。中间设有支柱，尺寸为1.0 m×0.9 m，房间、走道采用防火墙，站厅、站台楼梯口四周设有挡烟垂壁。站厅公共区和站台分别设置一个防烟分区，站厅公共区排烟量为7.886×104m3/h，站台区排烟量为8.544×104m3/h。地铁站台模拟三维示意图如图7所示。

图7 火灾模拟三维示意Fig. 7 Three-dimensional sketch of fire simulation model

由于站台为对称几何结构，仅考虑火源位于站台左侧的情况。火源A、B、C、D距站台左端位置分别为15、30、45、60 m，尺寸设置为1.0 m×1.0 m×0.1m，共设置16个工况模拟，如表2所示。s为火源距占台左端距离。沿站台顶棚下0.1 m设置一系列纵向热电偶，间隔1.0 m。环境温度设置为20 ℃，压力为101.325 kPa。为实现烟流的足够稳定状态，将模拟时间设置为300 s。

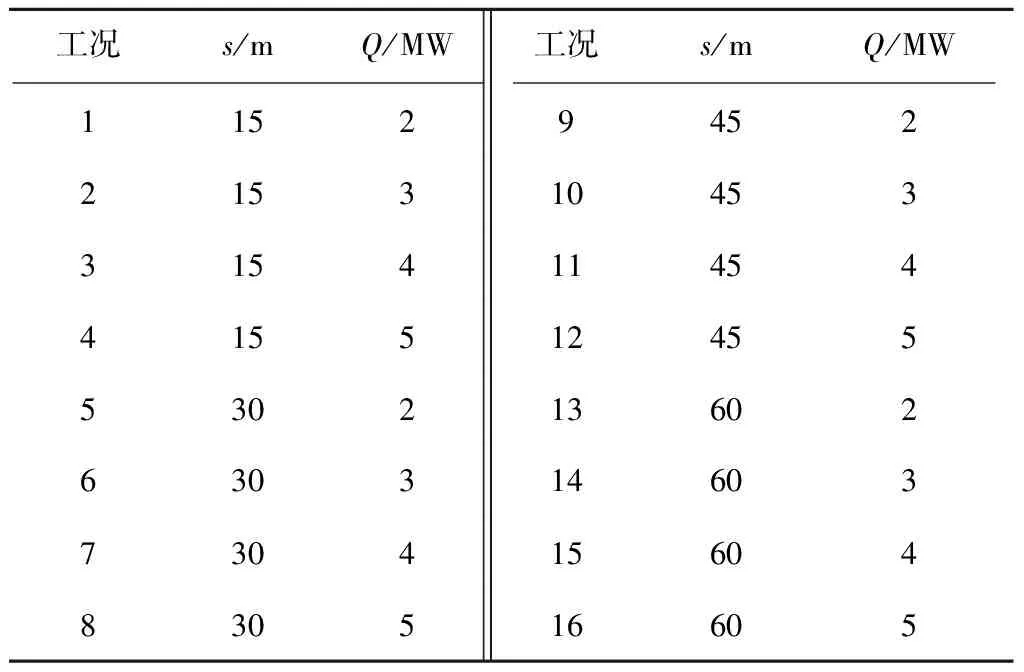
表2 全尺寸实验工况设置

3.2 顶棚下纵向烟温分布特征

站台内的火灾发生后会产生大量热量和烟气，热量在烟气中进行热传递，与外界产生温度差形成热浮力，烟气受到热浮力作用向上流动形成烟气羽流[14]，到达站台顶部，然后在顶棚下纵向蔓延。在运输过程中，烟气与冷空气相互作用，同时，大量的热量会向墙体和冷环境散发。这些因素的综合作用导致气温逐渐下降。在站台火灾中，温度变化受纵向距离的影响，通过研究不同火源位置和功率时顶棚下纵向烟气温度衰减规律，为疏散时烟气高温给人员带来的伤害提供有效帮助。

图8为Q=4 MW时不同火灾位置下站台顶棚下的纵向烟温分布，x轴是站台纵向距离。火源A、B、D的峰值温度分别为565、376、385 ℃，火源C的两峰值温度为335.6和364.9 ℃。如图8所示，最高峰值温度位于火源A处，因为火源A紧靠左侧设备房，燃烧时产生的烟气不断积累强化，不同于B、C、D产生的烟气能向两端扩散，从而使得A顶棚下的温度峰值最大。当火源位于C处时，出现两个峰值温度，这是由于C点距离楼梯口非常近，燃烧产生的烟雾一部分向上羽流形成最大的峰值温度，另小一部分顺着楼梯蔓延在楼梯口处的顶棚下形成较小的峰值温度。火源C、D峰值温度略小于D，因为C、D距楼梯处通风口较近，自然通风下烟气量略有减少。

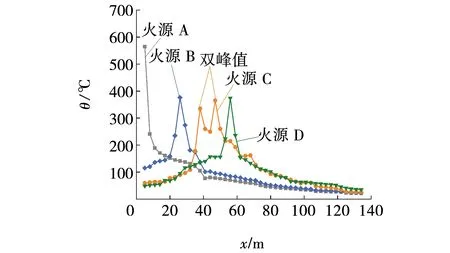
图8 Q=4 MW时顶棚下纵向烟温分布Fig. 8 Distribution of longitudinal smoke temperature under ceiling when Q=4 MW

在火源功率Q分别为2、3、4、5 MW时，距火源纵向距离对站台顶棚下烟气温度的影响如图9所示。图中D为距火源纵向距离，m；D=x-x0，x为测点位置，m；x0为火源位置，m。

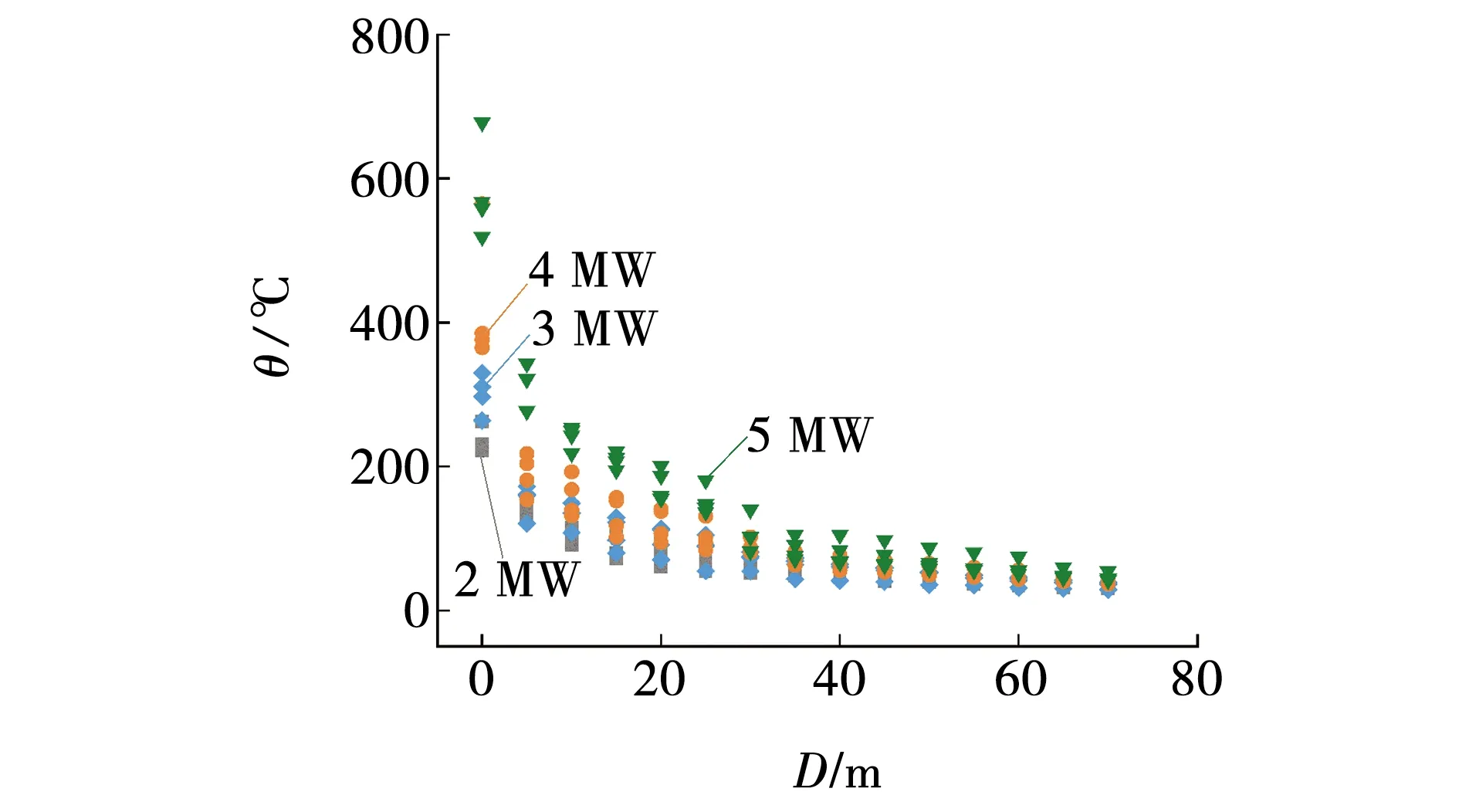
图9 随纵向距离增加顶棚下烟气温度变化Fig. 9 Flue gas temperature variation under ceiling with increasing longitudinal distance

由图9可知，随着与火源距离的增加，站台顶棚下烟气温度均呈指数衰减规律。距火源纵向距离小于5 m内，顶棚下温度衰减幅度最大；与火源距离5～30 m时温度变化减缓；当距离大于35 m时，顶棚下烟气温度基本保持在40～70 ℃之间。造成这一现象的主要原因是近火源处烟气浓厚，温度场变化明显，当距离足够大时，烟气量较少，分层较为稳定。热释放速率越大，最高温度分布差距越大，最大温度差在Q=4 MW时为ΔTmax-ΔTmin=200.76 ℃。在放热速率较小的情况下，距火源距离对最高温度的影响也减小，最小温差在Q=2 MW时为40.54 ℃。

3.3 顶棚烟温预测模型

为研究火灾时顶棚最高温度预测模型，引入几种经典模型并与模拟结果进行了比较，Alpert对无约束水平天花板进行了研究，提出了顶棚最高温度的预测公式，常用来研究地铁车站的顶棚最高温度。

(7)

式中：ΔTmax——顶棚最高温度，K；

Q——热释放速率，kW；

H——火源与顶棚的距离，m。

Ji针对地铁车站火灾中壁端对顶棚最高温度的影响进行了小规模实验和理论分析。在Alpert预测模型的基础上，提出了一种改进的最高温度预测模型[15]。

(8)

将式(8)除以式(7)可得

(9)

式中，ΔTmax,d——火源距端壁距离为d的顶棚最高温度，K。

2008年，Hu基于连续性和能量守恒方程，建立了预测烟层纵向温度分布的模型，即

，

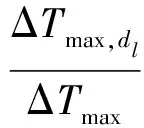
(10)

(11)

式中：ΔTmax,dl——距火源垂直距离最大温升，K；

dl——距火源垂直距离，m；

λ——热损失系数；

A——烟层与隧道边界的接触面面积，m2；

K——衰减系数。

FDS模拟中工况3最高温度为565 ℃，Alpert模型和Ji模型计算的顶棚下最高温度分别为682.43、696.94 ℃。可以看出，FDS的模拟结果低于预测结果，因为站台空间较大，通风良好，烟气层积聚相对较少。上述模型在工程实际应用中容易存在加大误差，因此，根据上述模型建立经验模型，可以得到站台火灾时，距火源纵向距离对顶棚温度遵循的规律模型，再根据模拟数据拟合得到的预测公式具有更高的可行性。

(12)

式中：ΔTmax,D——距火源纵向距离为d的顶棚最高温度，K；

ΔTmax——顶棚最高温度，K；

D——距火源纵向距离，m；

L——站台长度的一半；

a、k、b——系数。

图10所示为站台顶棚下无量纲峰值温度与无量纲距离。记无量纲峰值温度η=ΔTmax,D/ΔTmax，λ=D/L。火源A热释放功率Q为2 MW用A-2 MW的形式表示，由图10可以看出，随着无量纲距离的增加，无量纲峰值温度单调减小，而不受放热速率的影响，但随着D/L的增加，差异逐渐不明显。相关系数R2分别为0.96、0.91，站台顶棚下的最大烟温可表示为

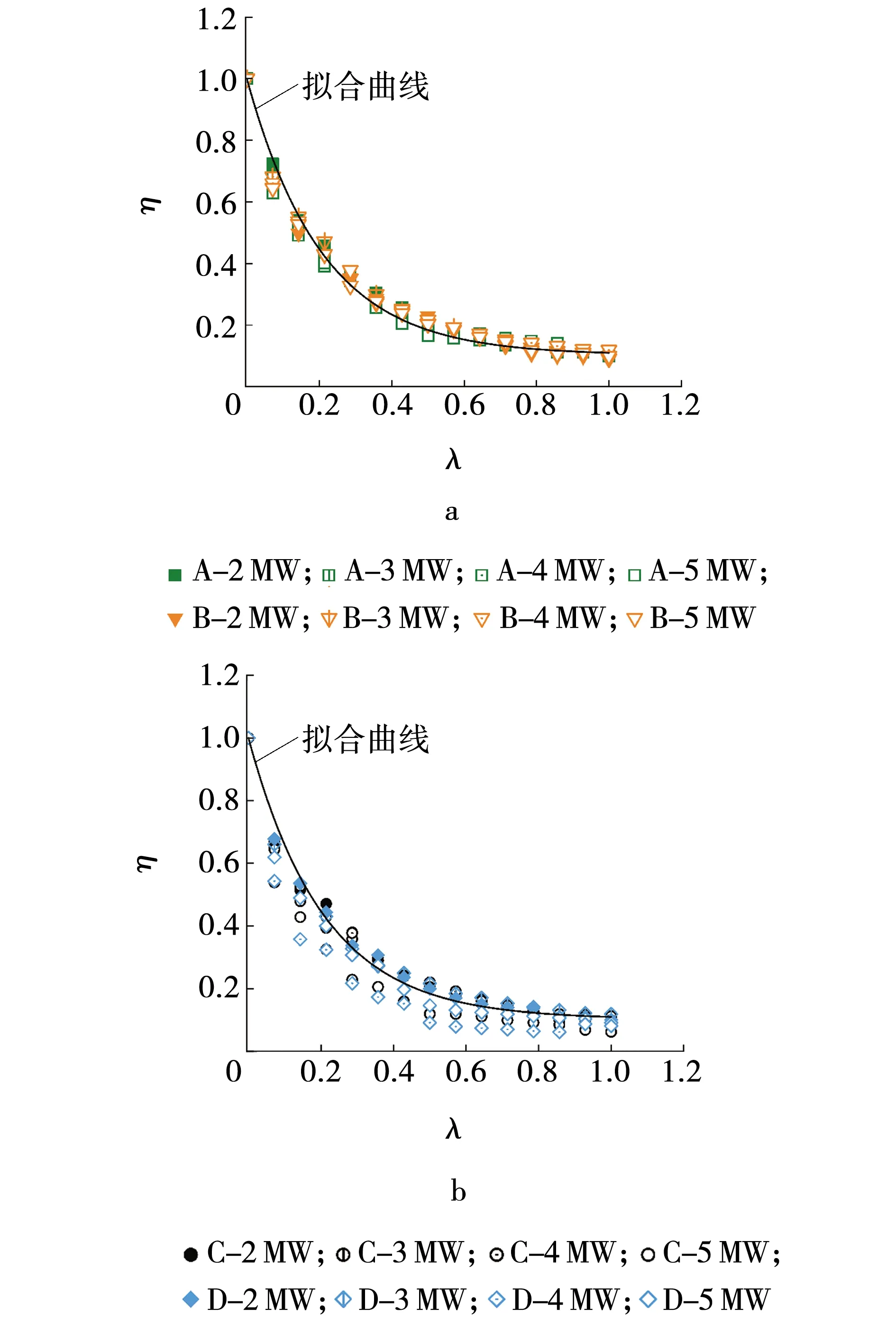
图10 拟合曲线Fig. 10 Fitting curve

(13)

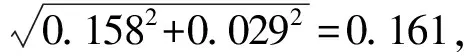
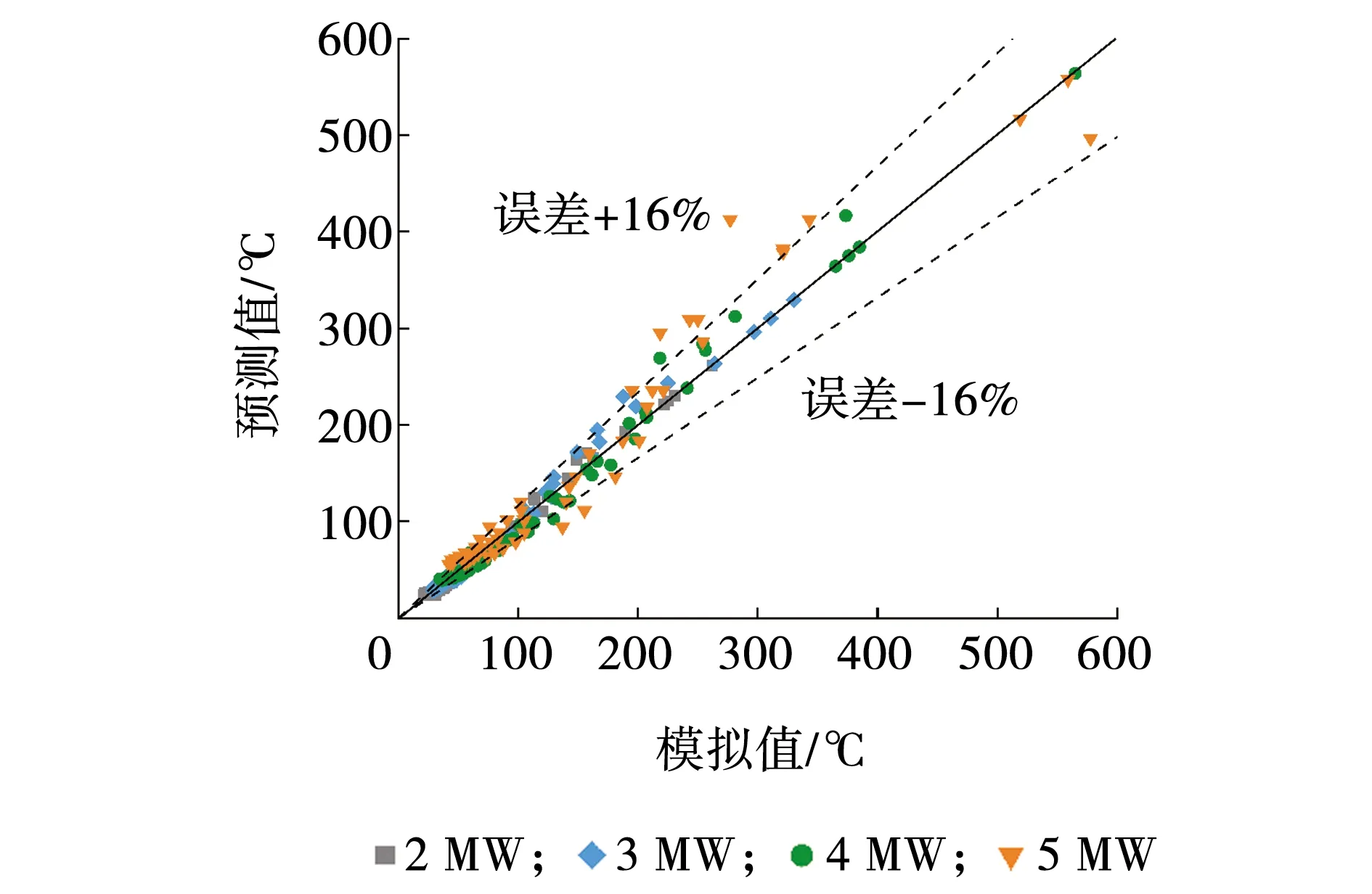
图11 纵向温升模拟值与预测值的比较Fig. 11 Comparison of simulated and predicted longitudinal temperature rise

4 结 论

(1)与隧道火灾相比，站台火灾顶棚下的烟温相对较低，受火源位置影响相对较小，因为站台空间较大，通风良好。站台顶棚下出现几个峰值温度取决于火源的位置，当火源位于站台楼梯口处时，烟气一部分顺楼梯蔓延在顶棚下积聚，才出现双峰值温度，其他位置均为单峰值温度。而火源位于站台端壁附近时，烟气流动相对较慢，温度与其余火源处相比较高，最高温差达200.76 ℃，最小温差40.54 ℃。

(2)考虑一般狭长封闭空间的隧道温度分布与本研究得到的结果不一致，建立了地铁站台顶棚下纵向烟气温度分布的无量纲峰值温度(ΔTmax,D/ΔTmax)经验模型。在数值模拟结果中，无量纲峰值温度(ΔTmax,D/ΔTmax)随无量纲距离(D/L)的增加呈指数衰减，而最大烟气温度仍位于火源的正上方，根据模拟数值和经验模型拟合可得预测公式。