直观演示让旋转运动变得通俗易懂

崔彦艳

[摘 要]“图形的变换”是对生活中对称、平移和旋转现象的抽象和延续，在学习这部分内容之前学生对轴对称图形已经了如指掌，对沿直线方向平移图形也有所了解。“图形的变换”教学中，教师通过直观演示加深学生对轴对称几何性质的认识，引导学生对已知图形进行变换，同时灵活运用图形变换绘制美术图案，发展学生的空间观念。

[关键词]直观操作;旋转运动;图形的变换

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）23-0036-02

课程标准指出：要考虑到学生的体验与理解便利、思考与探索的动机，尽可能地采取直观操作教学。课上直观操作可以帮助学生迅速产生感性认识，建立清晰具体的表象。小学生掌握数学概念主要依赖直观演示，否则，掌握概念会困难重重。因此，教学“图形的变换”时，教师可引导学生通过直观演示进行图形变换，从而发展学生的空间观念。

一、实物演示

教师在教学时要灵活机动地处理教材，整合各种有利的教学资源，让学习素材变得丰富多彩。实物演示形象生动，是宝贵的教学资源。例如，教学“轴对称”时，教师让一个五官端正、体态匀称的学生上台做“模特”，其他学生观察，思考“模特”的脸部是不是轴对称图形，学生反馈沿着“模特”面部中轴线假想出一条虚线，其左脸和右脸高度吻合，如果将脸面画到纸上，沿着这条中轴线对折，左、右脸完全重合，因此说“模特”的脸是左右对称的。

“模特”两只手侧平举，其他学生观察并判断人体是否沿着中心线左右对称;最后“模特”垂下一只手，其他学生再来判断，并说明依据。通过前后对比，深刻揭示对称、轴对称的意义、轴对称的判定依据，同时激发了学生的学习兴趣。

在教学“推想一个图形的轴对称图形”时，还是让一个五官端正、体态匀称的学生站到讲台上做“标本”，教师询问其他学生：“‘标本的面孔是否对称？眉眼口鼻呢？”学生异口同声地回答：“对称。”教师追问：“‘标本的对称轴是哪条线？”一名学生上讲台来比画。教师继续指引学生加强探究：用白纸把“标本”的右半边脸遮盖住，然后让学生估测他右眼的位置和右眉眉梢的位置，并思考能否勾画出右眼轮廓，怎样勾画，再让一个学生尝试画出右眼，其他学生进行来评判，画之前要先交待确定眉眼位置的方法。师生共同裁判并评议，给予指正和补充。

此时全体学生都积极投入到关于轴对称的趣味活动中。“标本”的双眼是轴对称的，要确定右眼的位置，必须以轴对称性质为推理依据，在对称轴的对称面找到“翻版”，选定若干个轮廓上的对应点，涂画出来，测量出对应点到对称轴的垂直距离，再按照左眼轮廓顺次连接对应点，勾勒出右眼外形。

二、学具演示

经过画眼的操作，学生不但了解了轴对称的几何性质，而且能将轴对称知识与生活现象有机结合，并借助轴对称的特征和性质去作图，形成丰富的想象力，同时，利用知识迁移为今后画出图形的对称图形打下坚实基础。画一个图形旋转90°后的图形时，学生经常只能画对变换后的旋转轴，其他部位则颠三倒四，如画出沿着顺时针方向旋转90°后的图案时，学生画对了机身的位置，但机翼的位置则发生错位，画成，这时教师用文具盒当机身，用白纸折出一对机翼贴在文具盒上，通过直观演示，学生立即醒悟。

但是，这种直观操作只能大致反映旋转运动的抽象特征：图形的旋转运动不改变图形的形状、大小，只改变摆放方向和角度，却不能对旋转变换进行定位分析，这一直观操作也只能起到辅助纠正作用。在遇到其他旋转变换时，学生又会犯难，要想确定图形旋转后的具体位置和坐标，还得从旋转的几何性质入手进行定量分析。

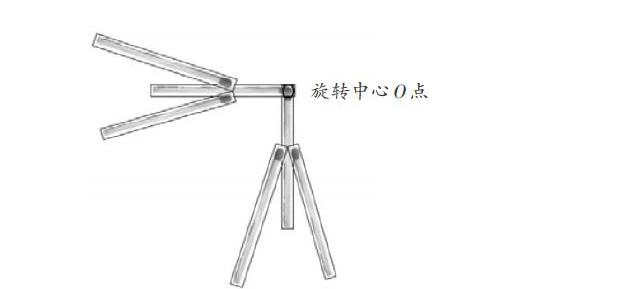
教学时，教师用火柴棒充当图形的边线，绕点O顺时针旋转90°后，让每根火柴棒都做出同样的位移变换，变换之后，对应顶点到旋转中心O等距，对应边、对应角大小不变，再让学生一一查找图形中的对应线段，并测量证实。这样，用移动的火柴棒的演示和测量长度的证明，从图形旋转的特征和性质两方面入手，研究一个简易平面图形旋转90°后位移图的画法，使学生悟出：旋转后图形的形状、大小维持原样，旋转中心的位置始终不变，旋转前后同一线段和同一夹角的大小都不变，唯一改变的就是摆放位置，从而建立精准、全面的表象，进而掌握旋转90°后新图的画法，并在操作中验证旋转的性质，凸显几何教学的本质。

三、肢体演示

肢体语言也是一种传递信息、表达思想的手段，用肢体演示，相对于其他表达途径，更加具有感染力。

例如，教学“旋转”时，教师以“请你用专业的数学语言精准描述物体的运动轨迹”作为核心任务开展教学。

（1）教师向左、向右、向前、向后走，要求学生采用一个准确的数学术语来描述。例如，教师向左行走3步，再向右行走5步，接着向前行走2步，最后向后行走1步，要求学生用专业的数学术语描述这一过程;再让一名学生陈述教师步行的方向和距离，另一名学生配合步行指令做踏步运动，其他学生监督和评论。这一活动是将平移知识进行游戏化展现，用肢体语言诠释平移的性质，使学生深刻体验平移的特点，搞清楚平移的两大要素：移动方向和移动距离，为类比迁移到旋转运动扎牢根基，同时激发学生的学习热情。

（2）教师原地旋转，要求学生用数学术语来描述。这是用肢体语言来诠释绕轴旋转的性质，让学生感受和认识旋转变换，建立表象，从而领会旋转变换的特性;再让学生分别用身体来做平移、旋转运动，辨析二者的区别，接着教师左右脚轮换单足旋转，让学生观察并回答哪条腿是旋转轴。旋转有三要素：旋轉中心、旋转方向和旋转角度。要精确地描绘出旋转后的图形，找准旋转中心是先决条件。这里，教师先解释旋转轴，就是为了能够类推迁移到旋转点。最后，教师继续做旋转运动，要求学生观察后概括出旋转运动中的变量与定量，也就是旋转的特征：旋转后，图形的形貌、大小都保持原状，只有方位发生改变。

（3）教师先后向四个方向做出旋转90°的转身运动，要求学生描绘出教师的转体方向和角度，让学生亲眼观察转体运动的转向和角度。小学生学习数学必须依仗原有经验，这种经验可作为学生学习相关知识的情境，是随手可用的。

上述的转体运动，为学生学习图形的旋转创设了现实情境和构建了模型，数学的趣味性体现得淋漓尽致，同时它又成为学习旋转知识的“活教材”，将旋转的内涵充分暴露出来，重新构建了学生对旋转的认知结构。

又如，教学“顺时针”“逆时针”概念时，教师伸直手臂，做出顺时针和逆时针旋转，要求学生分辨手臂的旋转方向，再让学生也照做，边做边配合解说是“顺时针”还是“逆时针”旋转，使学生身临其境地体验顺时针和逆时针的运动走向和路径，准确区分顺时针和逆时针，形成双向逆反的空间观念，从而使学习活动成为建构顺时针和逆时针概念的感性经验基础。

（责编 黄春香）