XGBoost-LSTM变权组合模型支持下短期PM2.5浓度预测——以上海为例

康俊锋,谭建林,方 雷,肖亚来

XGBoost-LSTM变权组合模型支持下短期PM2.5浓度预测——以上海为例

康俊锋1,谭建林1,方 雷2*,肖亚来1

(1.江西理工大学土木与测绘工程学院,江西 赣州 341000；2.复旦大学环境科学与工程系,上海 200433)

为进一步提高PM2.5浓度预测的精度,基于XGBoost和LSTM进行改进得到变权组合模型XGBoost-LSTM(Variable).过对预测因子进行相关性分析,得到其它大气污染物和气象因素对PM2.5浓度的影响,确定最优PM2.5浓度预测因子,再将预处理后数据集输入LSTM模型和XGBoost模型分别进行预测,采用基于残差改进的自适应变权组合方法得到最终预测结果.结果表明,污染物变量的相对重要性高于气象因子变量,其中当前PM2.5和CO浓度的相对重要性较高,而平均风速和相对湿度重要性较低.XGBoost-LSTM(Variable)模型的RMSE、MAE和MAPE值为1.75、1.12和6.06,优于LSTM、XGBoost、SVR、XGBoost-LSTM(Equal)和XGBoost-LSTM(Residual)模型.分季节预测结果表明,XGBoost-LSTM(Variable)模型在春季预测精度最好,而夏季预测精度较差.模型预测精度高的原因在于其不仅考虑了数据的时间序列特征,又兼顾了数据的非线性特征.

LSTM；XGBoost；PM2.5预测；变权组合

社会经济的快速发展导致PM2.5等空气污染问题日益突出[1-2],对PM2.5等空气污染物浓度进行精准预测和提前预警具有重要意义.PM2.5浓度预测模型主要包括以CAMQ[3](通用多尺度空气质量模型)模式、WRF-Chem[4](区域大气动力-耦合模型)模式和NAQPMS[5](嵌套空气质量预报模式系统)模式等为代表的机理模型,以多元统计理论、灰色预测模型(G,M)[6-7]、多元线性回归模型[8]等为代表的统计预报模型,以及以径向基神经网络(RBF)、反向传播神经网络(BP)、支持向量机(SVM)等神经网络发展到基于深度学习模型的神经网络,如:基于深度信念网络(DBNs)、长短期记忆神经网络(LSTM)等[9-12].

随着机器学习技术的发展,有研究采用历史气象数据或历史污染数据,利用支持向量回归模型[13]、随机森林[14-16]、BP人工神经网络[17]以及LSTM网络[18]等单机器学习模型,预测实时PM2.5浓度[19]、未来短期[20-21]和长期PM2.5浓度[14,22-23]及PM2.5浓度的空间变异[17]等.有研究通过构建多个单机器学习模型进行PM2.5浓度预测比较,LSTM网络在处理非线性时序数据方面性能高效并且有更好的泛化能力[24],XGBoost模型预测精度优于其他单机器学习模型[25].为进一步提高PM2.5浓度预测精度,有学者开始尝试组合多个机器学习模型来预测PM2.5浓度.宋国君等[26]和李建更等[27]分别建立了基于时间序列分解的SVR组合预测模型、Liu等[28]构建了DBN、LSTM网络和多层神经网络(MLP)的三模型组合模型.虽然组合预测模型相较于单机器学习模型可以提升和改善模型预测精度[29],但已有的组合模型研究都只是简单的将一个模型预测结果输入另一模型进行二次预测,或者将多个模型的预测结果进行简单求和.其特点类似一种“机械组合”,两种或多种组合模型之间未发生真正的“化学反应”.

此外,由于PM2.5浓度变化既受气象因素影响,也受空气污染物影响[30-31],但已有基于机器学习的PM2.5浓度变化预测研究大都只采用气象数据,或者只采用污染物浓度历史数据来进行PM2.5浓度预测,预测精度受限.因此,本研究尝试将气象数据、空气污染物数据和PM2.5浓度历史数据结合,在分析空气污染物和气象因素对PM2.5浓度影响基础上,设计了一种基于残差赋权[32]改进的自适应赋权方法,构建XGBoost模型和LSTM网络变权组合模型,对未来1h短期PM2.5浓度进行预测,以期为环境监测部门及社会公众提供预警及精准预测.

1 研究材料与方法

1.1 研究区域与数据

上海市(30°40′～31°53′N,120°52′～122°12′E)位于中国东部沿海的长江三角洲地区,是典型的特大型城市,面积约6340km2,地形起伏小,属于亚热带季风气候,其空气质量一直引人关注.本研究选取上海市10个环境监测站点(图1)2017年1月1日～10月31日逐小时历史空气质量浓度数据和气象数据(共7297组)数据,其统计性描述如表1所示.其中,近地面PM2.5浓度等空气质量数据来自于生态环境部部空气质量实时发布系统(http://106.37.208.233: 20035/),气象数据来自于欧洲中期天气预报中心3km´3km再分析数据(https://www.ecmwf.int/).

图1 研究区域

表1 上海市空气质量数据和气象数据统计性描述

1.2 研究方法

1.2.1 XGBoost XGBoost(Extreme Gradient Boosting)是一种集成的树模型,是GBDT(Gradient Boosting Decision Tree)的改进boosting算法,具有训练速度快、预测精度高等优点[33].XGBoost集成了多棵分类回归树(CART)以弥补单棵CART无法满足预测精度的不足,预测结果等于所有CART的得分总和[34].模型表示为:

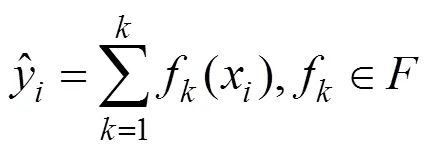
XGBoost通过对代价函数进行二阶泰勒展开,使用一阶和二阶导数,在训练集上可以更快收敛,有效提高训练速度,并且将正则化项加到损失函数上,可以降低模型的复杂度和过拟合的风险.

1.2.2 LSTM LSTM(Long Short-Term Memory)是RNN(Recurrent Neural Network)的改进模式,由Hpchreiter等[35]在1997年提出,采用LSTM层替换了传统的隐藏层,通过引入输入门、输出门、遗忘门三种“门”结构实现信息的有效筛选和长期记忆.LSTM内部结构如图2所示:

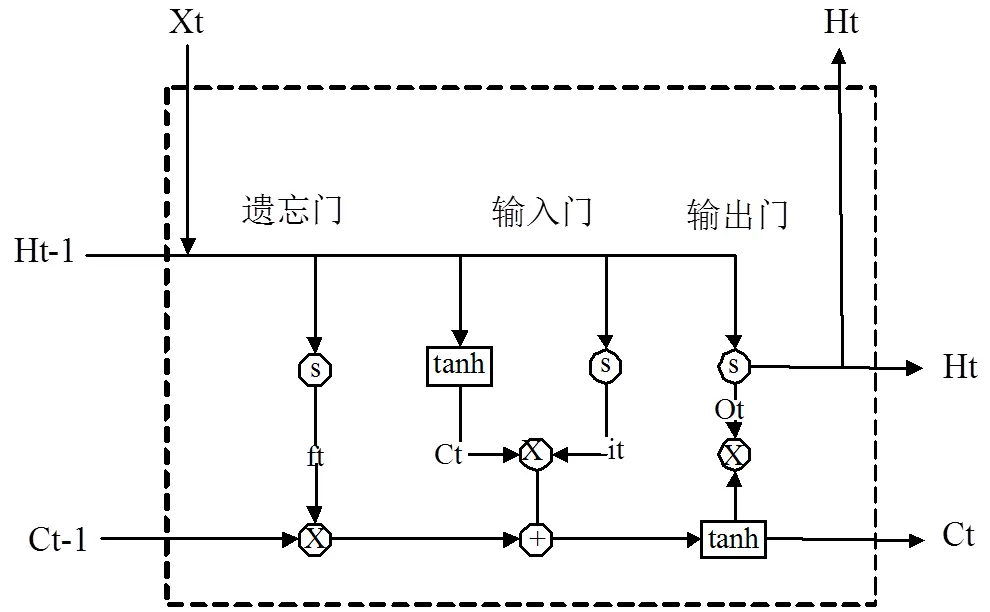
图2 LSTM模型结构

计算公式如下:

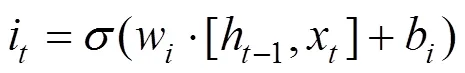
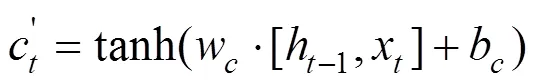
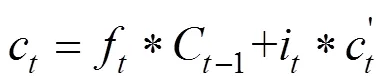
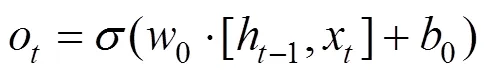
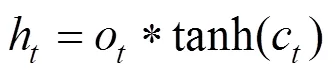
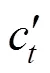
1.2.3 变权组合预测模型 本文构建三个组合模型:XGBoost和LSTM等值赋权组合模型XGBoost-LSTM(Equal)、XGBoost和LSTM残差赋权组合模型XGBoost-LSTM(Residual)以及XGBoost和LSTM变权组合模型XGBoost-LSTM (Variable).

(1) 单机器学习模型构建单机器学习模型的优劣决定组合模型的预测精度和性能,设置合理有效的超参数对于提高组合模型的预测性能和收敛速度具有重要意义[36].基于前人研究模型参数设置[37-38]对LSTM网络超参数进行设置,最终模型网络层数为2,学习率设置为0.001,激活函数设置为Tanh,优化算法选用Adam算法,迭代训练次数设置为100次,并设置学习率衰减为50次削弱为10%.

利用Scikit-learn提供的网格搜索(GridSearch)方法[39]对XGBoost模型的超参数寻优,模型参数最终设置为:max_depth=4,learning_rate=0.1,n_ estimators=200,subsample=0.7,colsample_bytree=0.85, silent=True,ganma=0.2.

(2)组合模型赋权组合模型精度与单机器学习模型的赋权有直接关系,赋权方法常见的有固定赋权与自适应赋权,其中固定赋权以等值赋权和残差赋权法最为常见[40].

等值赋权将单模型赋予相同的权重,而残差赋权组合模型表达为:

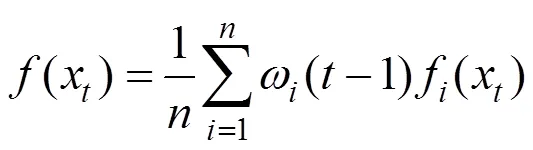
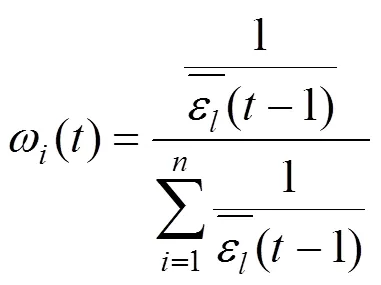
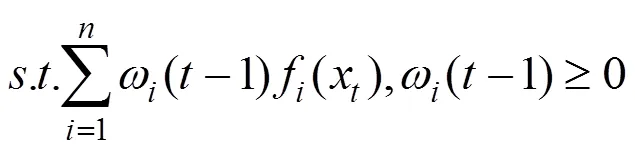
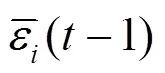
(3)改进的变权组合模型赋权方法本文使用基于残差赋权改进的自适应赋权方法的变权[41]方法构建了XGBoost-LSTM(Variable)模型.对于单机器学习模型在基于式(9)得到所有时刻残差赋权的权重基础上改进,计算最优值,使用前时刻权重平均值对本时刻模型进行初始赋权,即:

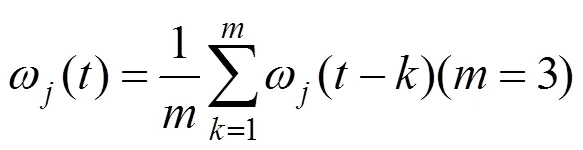
对于时刻,假设基于式(9)和式(11)得到各单机器学习模型权重后,计算该时刻组合模型的预测值与真实值的误差绝对值分别为e,t、e,t,则有:

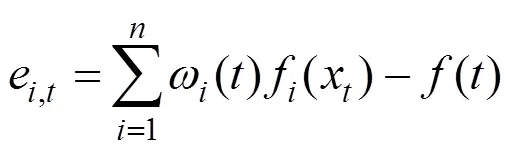
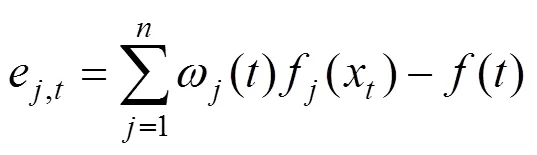
比较e,t和e,t值的大小,如果e,t<e,t则该组合模型用新的权重()代替原来的权重(),否则模型权重保持不变.

1.2.4 组合预测模型构建流程 组合预测模型构建流程如图3所示,包括数据预处理、单机器学习模型和变权组合预测模型构建以及模型评价分析.

图3 XGBoost-LSTM(Variable)模型预测流程

(1)数据预处理得到的原始数据集进行预处理,主要包括数据清洗、缺失值填充和归一化处理,本研究缺失值采用缺失前后数据均值补充.

(2)单机器学习模型构建数据集按照训练集:测试集=9:1比例划分后,在训练集上分别训练LSTM网络和XGBoost模型,确定模型最优超参数,保存训练模型.将测试集分别输入模型,得到各单机器学习模型预测结果.

(3)变权组合预测模型构建采用前文所示赋权方法确定各单机器学习模型的权重,计算得到组合模型最终预测结果.

(4)模型评价分析根据模型评价指标比较模型预测能力,分析模型预测效果.

1.2.5 评价指标 本研究采用常见的评价指标均方根误差(RMSE),平均绝对误差(MAE),平均绝对百分比误差(MAPE)以及相关系数(2)进行模型精度比较,指标的计算公式如下所示:

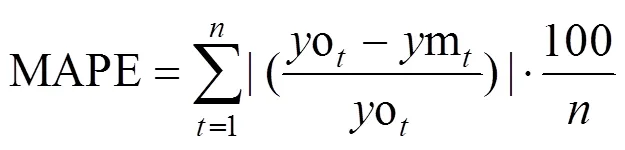
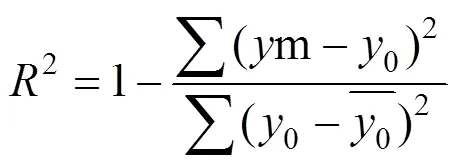
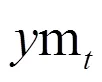
2 结果与讨论

2.1 预测结果的影响因子分析

2.1.1 空气污染物因子对PM2.5浓度的影响 PM2.5与其它空气污染物之间存在着物理化学层面的相互转化或者在传输过程之间产生相互影响[14],因此,对研究区PM2.5浓度与其它污染物变量之间进行了相关性分析.

如图4所示,分析PM2.5与其它大气污染物(CO,NO2,O3,PM10,SO2)之间的相关性,可以发现, PM2.5与各污染物之间均存在一定的相互关系.其中PM10、CO与PM2.5之间的相互关系极强,而O3与PM2.5之间的相关性最低,所以可以忽略O3对于PM2.5的影响,这与前人[14]的研究结果相同.

综上分析,将SO2、NO2和CO 3个污染物变量作为预测模型的输入,其中与PM2.5有极强相关性的PM10未加入到输入变量集中,因为经过实验分析PM2.5与PM10相关性过高导致产生冗余,从而导致精度降低.

图4 PM2.5与其他大气污染物的相关性分析

表2 PM2.5浓度与气象因素相关系数

2.1.2 气象因素对PM2.5浓度的影响 气象因子也是影响PM2.5浓度的一个重要因子,已有大量学者证明PM2.5浓度与风速、风向、湿度、气压、气温等因素之间具有密切关系[8,42-43].对研究区PM2.5与气象因素进行皮尔逊相关性分析,结果如表2所示.PM2.5与气象因子存在一定的相关性,其中PM2.5与气压和风向呈正相关关系,与气温、风速、边界层高度、相对湿度和降水量呈负相关关系.

在本研究中,气象因子作为辅助变量进行PM2.5浓度预测,因此气象因子所有变量均加入本文实验中.

2.2 变量重要性分析

利用训练好的XGBoost模型对输入变量的重要性进行评价,如图5所示,对于未来1h PM2.5浓度预测,变量重要性结果为污染物变量大于气象变量重要性,其顺序为当前PM2.5浓度、CO浓度、SO2浓度、NO2浓度、降水量、边界层高度、风向角度、平均气温、平均气压、平均风速、相对湿度.污染物变量中当前PM2.5浓度值和和CO浓度值重要性相对较高,而SO2、NO2浓度值重要性相对较低.气象因子变量中,降水量和边界层高度较为重要,平均风速和相对湿度的重要性相对较低.

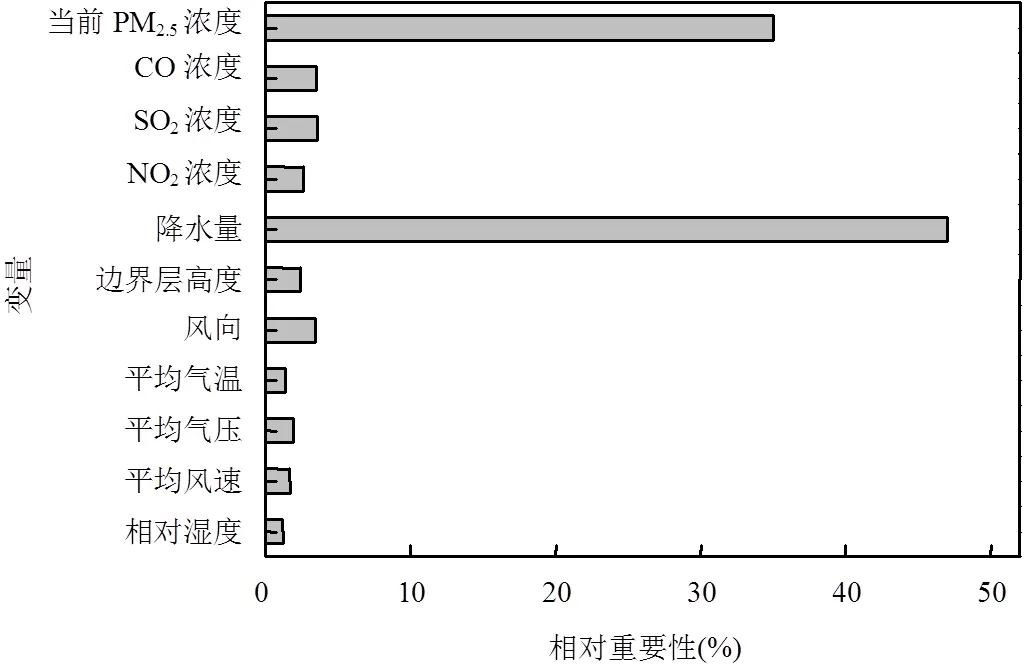
图5 变量重要性分析

2.3 短时预测分析与对比

为了验证改进的组合模型XGBoost-LSTM (Variable)精度,选择XGBoost、SVR、LSTM、XGBoost-LSTM(Equal)、XGBoost-LSTM(Residual)模型进行对比实验.不同模型预测值与实际值的对比如图6～7所示.

由图6可知,PM2.5浓度值实际值处于15～80ug/ m3时,各模型预测值和实际值的拟合度均较高,而对于实际值小于15ug/m3和大于80ug/m3的拟合效果均较差.单机器学习模型的拟合效果劣于组合模型的拟合效果,组合模型中,改进的变权组合模型与实际值的拟合效果最好,起伏程度更加接近PM2.5浓度变化的实际趋势,偏差较小.

由图7可知,组合模型的预测精度优于单机器学习模型和传统赋权方法组合模型预测精度.其中,改进的组合模型XGBoost-LSTM(Variable)的MAE、MAPE和RMSE值相较于XGBoost-LSTM(Equal)模型分别提升了27.3%、22.9%、32.7%,相较于XGBoost-LSTM(Residual)分别提升了20.6%、19.7%、15.1%,表明改进的变权组合方法具有更高的预测精度.

图6 各模型预测和实测结果对比

图7 不同模型实测值与预测值

2.4 不同季节预测分析

研究区属于典型亚热带季风性气候,季节气候存在明显差异,并且不同季节具有不同的污染物来源.因此针对不同季节选取典型月份进行预测分析,月份选取分别为春季(4月)、夏季(6月)、秋季(10月)和冬季(1月).

由图8可知,本研究改进的变权组合模型在春季和秋季的预测结果较好,其中春季即4月份为代表的预测精度最高,RMSE、MAE和MAPE各指标值分别为1.65、1.23和2.81,远小于其它季节的指标值;而在夏季和冬季的预测结果较差,其中夏季的预测结果最差,指标值分别为7.56、6.04和15.19.对于模型不同季节典型月份预测结果分析来看,造成夏季预测结果较差原因是由于夏季强烈的大气层活动,降雨频率高以及风速快,形成了较好的大气颗粒物扩散和清除的气象条件[44].而在冬季预测结果较好是由于PM2.5浓度与影响因子的相关性更好[25,45-46].

图8 组合模型四季典型月份预测结果

2.5 讨论

使用气象数据、空气污染物数据以及PM2.5浓度历史数据构建了变权组合模型.以上海为研究区域,进行未来1h短期PM2.5浓度预测.采用改进的XGBoost-LSTM(Variable)变权组合模型,RMSE、MAE和MAPE值为1.75、1.12和6.06,远小于瓮克瑞[47]提出的组合模型预测值8.901、6.774和8.862,以及Liu Hui[28]提出的集成模型4.51、2.78和7.79,是由于将时间序列预测模型中性能最好的LSTM网络和非线性模型中表现较好的XGBoost模型以变权组合的形式进行组合预测,该模型不仅考虑了数据的时间序列特征,又兼顾了数据的非线性特征;对于短时预测分析对比结果,本研究改进的XGBoost- LSTM(Variable)变权组合模型优于XGBoost- LSTM(Equal)组合模型、XGBoost-LSTM(Residual)组合模型,是由于本方法考虑到XGBoost模型和LSTM网络在不同时刻预测误差不同,通过对不同时刻采取不同的权重值,充分融合XGBoost模型和LSTM网络的优势.

研究区域选择中,不同地区的污染物组成以及气象条件具有强烈的地方性特点,因此,本研究只选取上海市作为研究区域探讨模型的表现.另外,在PM2.5预测影响因素选择上,本研究目前只将气象和空气质量污染物要素作为预测因子,未来应该考虑土地利用变化因素、经济、交通、环保政策等更多合适的因素进行预测研究,以进一步提高PM2.5预测精度.

3 结论

3.1 模型变量重要性分析可知,污染物变量的相对重要性高于气象因子变量重要性,其中当前PM2.5和CO浓度相对重要性高,而平均风速和相对湿度重要性较低.

3.2 由于组合模型不仅考虑了数据的时间序列特征,又兼顾了数据的非线性特征,因此,与单机器学习模型和其它组合模型结果相比,改进的变权组合模型的预测结果与真实值更加接近,误差更小,稳定性也更强,可以用于PM2.5浓度短期预警预报.

3.3 由于季节特征等差异,改进的组合模型在季节上的表现有所差异,表现为在春、秋季节预测效果较好,而在夏、冬季节预测结果较差.

[1] Kim Y, Manley J, Radoias V. Medium- and long-term consequences of pollution on labor supply: evidence from Indonesia [J]. IZA Journal of Labor Economics, 2017,6(1):1-15.

[2] 王庚辰,王普才.中国PM2.5污染现状及其对人体健康的危害[J]. 科技导报, 2014,32(26):72-78.

Wang G C, Wang P C. PM2.5pollution in China and its harmfulness to human health [J].Science & Technology Review, 2014,32(26):72-78.

[3] Dennis R L, Byun D W, Novak J H. The next generation of integrated air quality modeling: EPA's models-3 [J]. Atmospheric Environment, 1996,30(12):1925-1938.

[4] 周广强,谢 英,吴剑斌,等.基于WRF-Chem模式的华东区域PM2.5预报及偏差原因[J]. 中国环境科学, 2016,36(8):2251-2259.

Zhou G Q, Xie Y, Wu J B, et al.WRF-Chem based PM2.5forecast and bias analysis over the East China Region [J].China Environmental Science, 2016,36(8):2251-2259.

[5] Qingxin W, Qiaolin Z, Jinhua T, et al. Estimating PM2.5concentrations based on MODIS AOD and NAQPMS data over Beijing⁻Tianjin⁻Hebei. [J]. Sensors (Basel, Switzerland), 2019,19(5):1207.

[6] Zhang Z, Wu L, Chen Y. Forecasting PM2.5and PM10concentrations using GMCN(1,N) model with the similar meteorological condition: Case of Shijiazhuang in China [J]. Ecological Indicators, 2020,119: 106871.

[7] Pai T, Ho C, Chen S, et al. Using seven types of GM (1, 1) model to forecast hourly particulate matter concentration in Banciao City of Taiwan [J]. Water, Air, & Soil Pollution, 2011,217(1):25-33.

[8] 方晓婷,段华波,胡明伟,等.气象因素对大气污染物影响的季节差异分析及预测模型对比——以深圳为例[J]. 环境污染与防治, 2019, 41(5):541-546.

Fang X T, Duan H B, Hu W M,et al. The seasonal differential effects of meteorological parameters on atmospheric pollutants and the prediction model comparison: a case study of Shenzhen [J]. Environmental Pollution & Control, 2019,41(5):541-546.

[9] Liao Q, Zhu M, Wu L, et al. Deep learning for air quality forecasts: a review [J]. Current Pollution Reports, 2020:1-11.

[10] 戴李杰,张长江,马雷鸣.基于机器学习的PM2.5短期浓度动态预报模型[J]. 计算机应用, 2017,37(11):3057-3063.

Dai L J, Zhang C J, Ma L M,et al. Dynamic forecasting model of short-term PM2.5concentration based on machine learning [J].Journal of Computer Applications, 2017,37(11):3057-3063.

[11] 郑 毅,朱成璋.基于深度信念网络的PM2.5预测[J]. 山东大学学报(工学版), 2014,44(6):19-25.

Zheng Y, Zhu C Z. A prediction method of atmospheric PM2.5based on DBNs [J].Journal of Shandong University(Engineering Science), 2014,44(6):19-25.

[12] 朱晏民,徐爱兰,孙 强.基于深度学习的空气质量预报方法新进展[J]. 中国环境监测, 2020,36(3):10-18.

Zhu Y M, Xu A L, Sun Q. New progress for air quality forecasting methods based on deep learning [J].Environmental Monitoring in China,2020,36(3):10-18.

[13] 谢永华,张鸣敏,杨 乐,等.基于支持向量机回归的城市PM2.5浓度预测[J]. 计算机工程与设计, 2015,36(11):3106-3111.

Xie Y H, Zhang M M, Yang L, et al. Predicting urban PM2.5concentration in China using support vector regression [J].Computer Engineering and Design,2015,36(11):3106-3111.

[14] 侯俊雄,李 琦,朱亚杰,等.基于随机森林的PM2.5实时预报系统[J]. 测绘科学, 2017,42(1):1-6.

Hou J X, Li Q, Zhu Y J, et al. Real-time forecasting system of PM2.5concentration based on spark framework and random forest model [J].Science of Surveying and Mapping, 2017,42(1):1-6.

[15] 任才溶,谢 刚.基于随机森林和气象参数的PM2.5浓度等级预测[J]. 计算机工程与应用, 2019,55(2):213-220.

Ren C R, Xie G. Prediction of PM2.5concentration level based on random forest and meteorological parameters [J].Computer Engineering and Applications,2019,55(2):213-220.

[16] 夏晓圣,陈菁菁,王佳佳,等.基于随机森林模型的中国PM2.5浓度影响因素分析[J]. 环境科学, 2020,41(5):2057-2065.

Xia X S, Chen J J, Wang J J, et al. PM2.5concentration influencing factors in China based on the random forest model [J].Environmental Science,2020,41(5):2057-2065.

[17] 王 敏,邹 滨,郭 宇,等.基于BP人工神经网络的城市PM2.5浓度空间预测[J]. 环境污染与防治, 2013,35(9):63-66.

Wang M, Zou B, Guo Y, et al. BP artificial neural network-based analysis of spatial variability of urban PM2.5concentration [J].Environmental Pollution & Control, 2013,35(9):63-66.

[18] 白盛楠,申晓留.基于LSTM循环神经网络的PM2.5预测[J]. 计算机应用与软件, 2019,36(1):67-70.

Bai S N, Shen X L. PM2.5Prediction based on LSTM recurrent neural network [J].Computer Applications and Software,2019,36 (1):67-70.

[19] Zhang Y, Bocquet M, Mallet V, et al. Real-time air quality forecasting, part I: History, techniques, and current status [J]. Atmospheric Environment, 2012,60(1):632-655.

[20] 段大高,赵振东,梁少虎,等.基于LSTM的PM2.5浓度预测模型[J]. 计算机测量与控制, 2019,27(3):215-219.

Duan D G, Zhao Z D, Liang S H, et al. Research on PM2.5concentration prediction based on LSTM [J].Computer Measurement & Control, 2019,27(3):215-219.

[21] Liu D, Sun K. Short-term PM2.5forecasting based on CEEMD-RF in five cities of China [J]. Environmental Science and Pollution Research, 2019,26(32):32790-32803.

[22] Huang K, Xiao Q, Meng X, et al. Predicting monthly high-resolution PM2.5concentrations with random forest model in the North China Plain [J]. Environmental Pollution, 2018,242.

[23] Mao X, Shen T, Feng X. Prediction of hourly ground-level PM PM2.5concentrations 3days in advance using neural networks with satellite data in eastern China [J]. Atmospheric Pollution Research, 2017,8(6):1005-1015.

[24] 赵文芳,林润生,唐 伟,等.基于深度学习的PM2.5短期预测模型[J]. 南京师大学报(自然科学版), 2019,42(3):32-41.

Zhao W F, Lin R S, Tang W, et al. Forecasting model of short-term concentration based on deep learning [J].Journal of Nanjing Normal University (Natural Science Edition),2019,42(3):32-41.

[25] 康俊锋,黄烈星,张春艳,等.多机器学习模型下逐小时PM2.5预测及对比分析[J]. 中国环境科学, 2020,40(5):1895-1905.

Kang J F, Huang L X, Zhang C Y, et al.Hourly PM2.5prediction and its comparative analysis under multi-machine learning model [J].China Environmental Science, 2020,40(5):1895-1905.

[26] 宋国君,国潇丹,杨 啸,等.沈阳市PM2.5浓度ARIMA-SVM组合预测研究[J]. 中国环境科学, 2018,38(11):4031-4039.

Song G J, Guo X D, Yang X, et al.ARIMA-SVM combination prediction of PM2.5concentration in Shenyang [J]. China Environmental Science, 2018,38(11):4031-4039.

[27] 李建更,罗奥荣,李晓理.基于互补集合经验模态分解与支持向量回归的PM2.5质量浓度预测[J]. 北京工业大学学报, 2018,44(12): 1494-1502.

Li J G, Luo A R, Li X l.Prediction of PM2.5mass concentration based on complementary ensemble empirical mode decomposition and support vector Regression [J].Journal of Beijing University of Technology, 2018,44(12):1494-1502.

[28] Liu H, Dong S. A novel hybrid ensemble model for hourly PM2.5forecasting using multiple neural networks: a case study in China [J]. Air Quality, Atmosphere & amp; Health, 2020:1-10.

[29] 王学梅,王凤文,陈 滔,等.基于组合模型的PM2.5浓度预测及其不确定性分析[J]. 环境工程, 2020,38(8):229-235.

Wang X M, Wang F W, Chen T, et al.PM2.5concentration prediction and uncertainly analysis based on a composite model [J].Environmental Engineering,2020,38(8):229-235.

[30] Wang J, Shao W, Kim J. Multifractal detrended cross-correlation analysis between respiratory diseases and haze in South Korea [J]. Chaos, Solitons and Fractals: the Interdisciplinary Journal of Nonlinear Science, and Nonequilibrium and Complex Phenomena, 2020,135:10.1016/j.Chaos.2020.109781.

[31] Chen J, Lu J, Avise J C, et al. Seasonal modeling of PM2.5in California's San Joaquin Valley [J]. Atmospheric Environment, 2014,92:182-190.

[32] 王新民,崔 巍.变权组合预测模型在地下水水位预测中的应用[J]. 吉林大学学报(地球科学版), 2009,39(6):1101-1105.

Wang X M, Cui W. Application of changeable weight combination forecasting model To groundwater level prediction [J]. Journal of Jilin University (Earth Science Edition), 2009,39(6):1101-1105.

[33] Dietterich T G. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting, and randomization [J]. Machine Learning, 2000,40(2):139-157.

[34] Wu Y, Qi S, Hu F, et al. Recognizing activities of the elderly using wearable sensors: a comparison of ensemble algorithms based on boosting [J]. Sensor Review, 2019,39(6):743-751.

[35] Hochreiter S, Schmidhuber J. Long Short-Term Memory [J]. Neural Computation, 1997,9(8):1735-80.

[36] 郭立力,赵春江.十折交叉检验的支持向量机参数优化算法[J]. 计算机工程与应用, 2009,45(8):55-57.

Guo L L, Zhao C J. Optimizing parameters of support vector machine's model based on genetic algorithm [J].Computer Engineering and Applications, 2009,45(8):55-57.

[37] Zhai W, Cheng C. A long short-term memory approach to predicting air quality based on social media data [J]. Atmospheric Environment, 2020,237.

[38] Chang Y, Chiao H, Abimannan S, et al. An LSTM-based aggregated model for air pollution forecasting [J]. Atmospheric Pollution Research, 2020,11(8):1451-1463.

[39] Gang L, Jingying F, Dong J, et al. Spatial variation of the relationship between PM2.5concentrations and meteorological parameters in China [J]. BioMed Research International, 2015,2015,684618.

[40] 刘 明,王红蕾,索良泽.基于变权组合模型的中长期负荷概率密度预测[J]. 电力系统及其自动化学报, 2019,31(7):88-94.

Liu M, Wang H L, Suo L Z. Medium-and long-term load probability density forecasting based on variable weight combination model [J].Proceedings of the CSU-EPSA, 2019,31(7): 88-94.

[41] 王新民,崔 巍.变权组合预测模型在地下水水位预测中的应用[J]. 吉林大学学报(地球科学版), 2009,39(6):1101-1105.

Wang X M, Cui W. Application of changeable weight combination forecasting model to groundwater level prediction [J].Journal of Jilin University (Earth Science Edition), 2009,39(6):1101-1105.

[42] 曲 悦,钱 旭,宋洪庆,等.基于机器学习的北京市PM2.5浓度预测模型及模拟分析[J]. 工程科学学报, 2019,41(3):401-407.

Qu Y, Qian X, Song H Q, et al. Machine-learning-based model and simulation analysis of PM2.5concentration prediction in Beijing [J].Chinese Journal of Engineering,2019,41(3):401-407.

[43] 谢 超,马民涛,于肖肖.多种神经网络在华北西部区域城市空气质量预测中的应用[J]. 环境工程学报, 2015,9(12):6005-6009.

Xie C, Ma M T, Yu X X. Forecasting model of air pollution index based on multi-artificial neural network in western region of Northern China [J].Chinese Journal of Environmental Engineering,2015,9(12): 6005-6009.

[44] 刘小真,任羽峰,刘忠马,等.南昌市大气颗粒物污染特征及PM2.5来源解析[J]. 环境科学研究, 2019,32(9):1546-1555.

Liu X Z, Ren Y F, Liu Z M, et al. Pollution characteristics of atmospheric and source apportionment of PM2.5in Nanchang City [J].Research of Environmental Sciences,2019,32(9):1546-1555.

[45] 张淑平,韩立建,周伟奇,等.冬季PM2.5的气象影响因素解析[J]. 生态学报, 2016,36(24):7897-7907.

Zhan S P, Han L J, Zhou W Q, et al. Relationships between fine particulate matter(PM2.5) and meteorological factors in winter at typical Chinese cities [J].Acta Ecological Sinical,2016,36(24):7897- 7907.

[46] 朱媛媛,高愈霄,刘 冰,等.京津冀秋冬季PM2.5污染概况和预报结果评估[J]. 环境科学, 2019,40(12):5191-5201.

Zhu Y Y, Gao Y X, Liu B, et al. Concentration characteristics and assessment of model-predicted results of PM2.5in the Beijing- Tianjin-Hebei Region in autumn and winter [J].Environmental Science,2019,40(12):5191-5201.

[47] 翁克瑞,刘 淼,刘 钱. TPE-XGBOOST与LassoLars组合下PM2.5浓度分解集成预测模型研究[J]. 系统工程理论与实践, 2020, 40(3):748-760.

Weng K R, Liu M, Liu Q. An integrated prediction model of PM2.5concentration based on TPE-XGBOOST and LassoLars [J].Systems Engineering-Theory & Practice,2020,40(3):748-760.

Short-term PM2.5concentration prediction based on XGBoost and LSTM variable weight combination model: a case study of Shanghai.

KANG Jun-feng1, TAN Jian-lin1, FANG Lei2*, XIAO Ya-lai1

(1.School of Civil and Surveying & Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China；2.Department of Environmental Science and Engineering, Fudan University, Shanghai 200433,China)., 2021,41(9)：4016～4025

In order to further improve the accuracy of PM2.5concentration prediction, a variable weight combination short-term 1-hour PM2.5concentration prediction model based on LSTM network and XGBoost model was proposed.First, analyze the predictive factors, explore the influence of air pollutant factors and meteorological factors on the PM2.5concentration, to determine the best PM2.5concentration predictive factors and analysis the variable importance. Then, after data pretreatment the LSTM prediction model and the XGBoost prediction model was built respectively, and adopt the adaptive variable weight combination method based on residual improvement to obtain the final prediction result. The results show that: The relative importance of pollutant variables is higher than the importance of meteorological factors, among which the relative importance of current PM2.5concentration and CO concentration is higher, while the importance of average wind speed and relative humidity is lower. The values of RMSE, MAE and MAPE of the variable weight combined XGBoost-LSTM (Variable) model proposed in this study are 1.75, 1.12 and 6.06, which are better than LSTM, XGBoost, SVR, XGBoost-LSTM (Equal) and XGBoost-LSTM (Residual) model. The combined model predicts performance best in spring but the forecast accuracy is poor in summer. The variable weight method combination model proposed in this study effectively combines the advantages of the two models, not only considers the time series information of the data but also takes into account the nonlinear relationship between the features, and has higher prediction accuracy compared with other models.

long short term memeny (LSTM)；XGBoost；PM2.5forecast；variable weight combination model

X831

A

1000-6923(2021)09-4016-10

康俊锋(1978-),男,江西赣州人,副教授,博士,主要从事高性能GIS算法及其在环境与土地中的应用研究.发表论文10余篇.

2021-01-26

国家重点研发计划项目(2016YFC08033105);国家留学基金资助项目(201808360065);江西省教育厅科学技术研究项目(GJJ150661);国家自然科学基金青年基金资助项目(41701462)

*责任作者, 博士, fanglei@fudan.edu.cn