基于神经网络编码的真值发现*
曹建军,常 宸,2,翁年凤,陶嘉庆,3,江 春
(1.国防科技大学第六十三研究所,江苏 南京 210007;2.陆军工程大学指挥控制工程学院,江苏 南京 210007; 3.南京工业大学工业工程系,江苏 南京 210009)
1 引言
如今,数据在各行各业中发挥着越来越重要的作用,但数据中存在的各种问题也日益凸显。由于缺乏有效的控制手段,不同互联网平台提供的数据质量存在差异,错误、过时、不完整数据的存在导致多个网站针对同一实体的描述存在冲突[1]。这里的冲突是指不同数据集对同一实体具有不一致的描述[2]。例如,不同网站对同一地点同一天的天气情况提供不同的信息,各图书网站为同一书籍提供不同的作者信息等。这些不一致信息可能来源于信息录入错误、语义理解偏差和数据抽取错误等。低质量的冲突数据可能会导致错误的分析决策和预测,对效益产生巨大的影响[3]。因此,解决数据冲突问题格外关键且迫在眉睫。真值发现研究如何从多个数据源提供的多个对象的冲突描述中为每一个对象找出最准确的描述[4]。
传统真值发现方法分为基于迭代的方法、基于优化的方法和基于概率图模型的方法。这几类方法假设数据源可靠度与观测值可信度之间的关系可用简单函数表示,通过人工定义迭代规则或假设数据分布进行真值发现。而实际上,数据源可靠度和观测值可信度之间的关系通常是未知的,简单函数不足以表达这种复杂的关系,同时人工定义的条件难以反映数据的真实底层分布,导致真值发现的结果准确性不高。近年来,神经网络被应用到与真值发现类似的场景中,有学者利用神经网络学习数据源可靠度与观测值可信度之间的关系,提高了真值发现的效率和稳定性,但仅适用于二值属性的真值发现,不适用于冲突消解的一般场景。
与传统真值发现方法不同,本文首先基于经常提供相同观测值的数据源应具备相似可靠度的假设,提出 “数据源-数据源”损失;基于可靠数据源更可能提供可信观测值的假设,提出“数据源-观测值”损失。之后,设计双损失深度网络模型,对数据源可靠度与观测值可信度进行编码。网络优化过程一方面使可靠的数据源与可信的观测值在嵌入空间接近,另一方面使可靠的数据源在嵌入空间也彼此接近,并与不可靠的数据源远离。最后,利用数据源与观测值的高维嵌入空间进行真值发现。
与传统方法相比,本文利用神经网络表达数据源可靠度与观测值可信度间复杂的关系,避免了人工定义和假设数据分布对真值发现结果的影响,更准确地捕捉数据源与观测值间的依赖关系。同时,利用向量表达数据源可靠度与观测值可信度较实数更准确。与近期提出的基于神经网络的方法相比,所提方法TDNNE(Truth Discovery based on Neural Network Encoding)适用于真值发现的一般场景。实验结果也表明该方法优于已知真值发现方法。
2 相关工作
2.1 真值发现基本方法
针对结构化数据的真值发现,一种简单直接的方法是进行投票或取平均,这种方法假设所有数据源同样可靠。然而在大多数情况下这种假设可能不成立,不同来源的信息质量可能差异很大。真值发现方法通过估计数据源可靠度来提高冲突消解的准确性。由于实际中往往缺乏数据源质量的先验知识,数据源信息需要从已知数据中挖掘[5,6]。现阶段,已有真值发现方法将数据源可靠度估计与真值发现过程紧密结合,设计不同的真值发现模型以适应不同的冲突消解场景,从不同数据源提供的冲突信息中找到正确信息。
Yin等人[4]首先提出了真值发现的概念,并给出了TruthFinder算法。该算法基于2个假设:(1)越可靠的数据源提供的事实越可信;(2)提供越多可信事实的数据源越可靠。该假设综合考虑了数据源的真实性与其所提供的所有观测值的准确性。众多学者基于此假设提出了不同的真值发现方法,可概括为基于迭代的方法、基于优化的方法、基于概率图模型的方法和基于神经网络的方法4类。
基于迭代的方法[7,8]将真值发现过程设计为迭代过程,利用简单函数假设数据源与观测值间的关系,迭代进行真值计算步骤和数据源可靠度估计,直至收敛。以文献[8]为例,真值计算过程中,固定数据源可靠度,以加权投票的方式计算真值,同时数据源可靠度则由本次迭代真值计算得到。
基于优化的方法[9 - 11]假设对象的真值情况应该尽可能与各数据源提供的观测值接近,数据源质量越高,则其提供的对象属性集合与真值集合越相似。该方法通过设置目标函数来进行真值发现,将真值发现问题转化为优化问题求解。通常,基于优化的方法使用坐标下降法[12]来计算目标函数中数据源可靠度与观测值可信度2个参数。通过固定一个参数的值,寻找另一个参数的最优值,迭代地执行真值计算步骤和数据源可靠度估计步骤,直到收敛,这与基于迭代的方法类似。
基于概率图模型的方法[13 - 16]假设观测值服从概率分布,通过采样和参数估计的方法估计真值,若假设的概率分布不能反映数据的真实分布,将导致真值发现结果不理想。
传统的真值发现方法假设数据源可靠度和观测值可信度之间的关系可以通过函数(如线性函数和二次函数等)来表示。而实际上,数据源可靠度和观测值可信度之间的关系通常是先验未知的,简单假设将会导致真值发现的结果并不理想。Marshall等人[17]首次将神经网络应用到真值发现问题中,利用前馈神经网络解决社会感知问题,但这种方法需要人工标记部分对象,无法进行无监督的学习,且仅适用于网络观测值是否为真的判断,不适用于真值发现的一般场景。文献[18-19]利用受限玻尔兹曼机隐含层学习数据源可靠度分布,采用对比散度算法(Contrastive Divergence)训练模型参数[20],通过吉布斯采样,达到了较好的拟合效果。但是,由于受限玻尔兹曼机本身的局限性,也仅适用于属性为二值的真值发现场景。之后,Li等人[21]利用长短时记忆神经网络进行真值发现,以不同数据源提供的“对象-属性-值”矩阵与数据源可靠度矩阵的乘积作为输入,以各个观测值作为真值的概率作为输出,通过最小化真值与各数据源观测值之间的距离来优化网络参数。该模型首次利用比实数具有更好的表示能力的向量来表示数据源可靠度,将数据源的可靠度视为潜在的背景知识,并存储在可靠度矩阵中用来计算观测值的可信度。
总结以上几类真值发现方法,首先,基于迭代的方法由于人工设置迭代规则,具备较好的可解释性,以方法Investment[8]为例,数据源将其可靠度“投资”在其提供的观测值上,同时从识别真值中收获可靠度,而其余3种方法则通过梯度下降或参数估计的方法获得真值,可解释性相对较差[22]。另一方面,有关数据源的先验知识对于真值发现结果的提升至关重要,在基于优化的方法中,先验知识可以被定义为额外的等式或不等式约束,而在基于概率图模型的方法中,先验知识可帮助模型中的超参数获得更多的额外信息。基于迭代、优化和概率图模型的真值发现方法由于简单假设数据分布或数据源观测值间依赖关系,常常不能准确地描述数据的底层分布,导致真值发现结果不理想。
2.2 不同场景下的真值发现方法
针对真值发现问题,学者们通过考虑影响真值发现的各种因素及不同的应用场景进行了一系列相关研究。表1所示为不同真值发现场景的特点及其所需解决的问题的对比分析。

Table 1 Comparative analysis of the features and problems in different truth discovery scenarios表1 不同真值发现场景的特点及其问题对比分析
2.2.1 数据流
在数据流应用方面,Li等人[23]研究了数据流上的真值发现,将真值发现问题中最常见的最优化模型近似转化为概率模型,提出能随着新数据的加入而动态更新实体真实性和数据源权重的增量真值发现框架。李天义等人[24]等人针对感知数据流上的连续真值发现问题进行了研究,通过结合感知数据本身及其应用特点,定义并研究了当感知数据流真值发现的相对误差和累积误差较小时,相邻时刻数据源的可信度变化需要满足的条件,进而给出了一种概率模型,以预测数据源的可信度满足该条件的概率,在保证真值发现结果达到用户给定精度的同时提高了效率。Ouyang等人[25]针对大规模流数据,利用MapReduce框架设计了一种并行可增量的真值发现算法,并行算法能有效地在大型数据集中发现真值,流算法能处理增量的数据。
2.2.2 群智感知
在群智感知中,真值发现是指通过聚合有用的感知数据来推断真实信息,同时从收集到的感知数据中估计用户可靠性的过程。Yang等人[26]针对群智感知数据流,将质量评估与货币激励相结合,设计了一种无监督的学习方法来量化用户的数据质量和长期的声誉,并利用一个离群的检测技术来过滤异常的数据项。此外,还将盈余分享的过程建模为一种合作博弈,并提出了一种基于Shapley值的方法来确定每个用户的支付。通过这个质量相关的支付方案,可以防止“搭便车”的问题,也可以激励用户提供高质量的数据。Zheng等人[27]考虑了群智感知的隐私方面,提供了自定义和低开销的协议,通过估算用户的可靠性和隐私保护来推断真实信息。此外,还提出了一种基于同态加密的替代设计,它利用双服务器模型来保持用户端的效率,以进一步提高协议在大规模人群感知应用中的可用性。Huang等人[28]引入时间敏感性,并用最大期望估计来确定描述准确性和数据源可信度。Miao等人[29]则通过设计一个轻量型的真值发现架构,建立新的真值发现方案,解决最大似然估计问题,同时确定声明的正确性和数据源可靠性,不仅保护了感知数据和用户可靠的信息,还减少了开支。
2.2.3 文本数据
针对文本数据真值发现,目前大部分学者对问题进行了简化,对文本数据进行粗粒度的分析,只能对社交媒体或其他网络资源中文本数据进行是否为真的判断,将问题简化为二值属性的真值发现问题。Popat等人[30]构建“数据源-语言风格”输入向量作为输入,通过Logistic回归,将真值发现问题转化为二分类问题;Broelemann等人[18,19]利用受限玻尔兹曼机隐含层学习真值概率分布,由于受限玻尔兹曼机本身特性,也只能用于二值属性的真值发现;Marshall等人[17]利用全连接神经网络学习数据源可靠度与观测值可信度间的关联关系,同样将用户答案抽象为0/1这2类,并输入网络进行真值发现。对于一般意义下的真值发现,文献[31]首先将文本信息引入到真值发现过程中,并提出了细粒度的非结构化数据真值模型。Ma等人[32]提出了一个概率图模型,以无监督发现药物的真正副作用。 对于一般意义的文本数据真值发现,Zhang等人[33]将文本的语义信息完全融合到真值发现的过程中,并提出了一种从众包用户中发现可信赖答案的方法。然而,该方法只能处理答案较短的情况,不能应用于大多数文本数据真值发现场景。在此基础上,Li等人[34]将从特定问题的答案中提取的关键词组合成多个可解释的因子,并使用基于概率图模型的方法进行真值发现,以找到值得信赖的答案。
3 问题定义
本文主要研究结构化数据真值发现问题,设计双损失网络对数据源及观测值进行编码,利用神经网络自动挖掘数据源与观测值之间的关联度。下面介绍结构化数据真值发现问题及相关定义。
如表2所示为8个网站关于同一航班AA-1223-DFW-DEN提供的不一致的相关信息。首先每个网站提供的航班信息均有所缺失,同时多个数据源提供的航班信息之间存在冲突。

Table 2 Information of flight AA-1223-DFW-DEN表2 航班AA-1223-DFW-DEN的相关信息
本文研究的问题描述如下:给定对象集合E={ei|i=1,2,…,Q},其中Q是对象数量,ei表示第i个对象;数据源集合S={sj|j=1,2,…,M},数据源提供对象的描述信息,sj表示第j个数据源,M表示数据源数量;对象ei的观测值集合Ci={cik|k=1,2,…,N},其中cik表示对象ei第k个观测值,N表示该对象观测值数量;ci*表示对象ei的真值。
本文解决在不进行人工标注的情况下,从多个数据源提供的多源冲突观测值中找到对象信息的真值,即给定对象集合E及提供其描述的数据源集合S,评估数据源质量,找出各个对象对应的真值。
4 模型与分析
4.1 数据源观测值编码
本节介绍数据源观测值编码过程,根据所提编码假设,目标嵌入空间如图1所示。图1中不同填充内容的点分别表示不同数据源可靠度编码与观测值可信度编码在嵌入空间中的位置。首先,对于不同数据源,设计“数据源-数据源”损失,使得可靠度相似的数据源在嵌入空间也彼此接近;对于观测值,设计“数据源-观测值”损失,使得观测值可信度向量在嵌入空间与其数据源接近。通过将数据源与观测值间的关系嵌入到高维空间,充分挖掘数据源观测值间的信息,基于此空间完成真值发现。
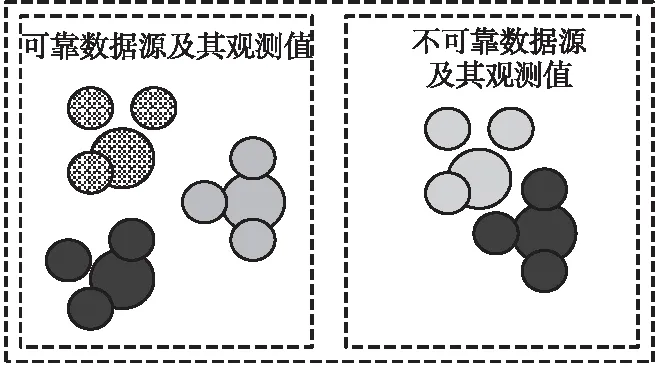
Figure 1 Illustration of objective embedding space图1 目标嵌入空间示意图
4.1.1 “数据源-数据源”损失
基于经常提供相同观测值的数据源应具备相似可靠度的假设,设计“数据源-数据源”损失,对数据源进行编码。设数据源si和sj的嵌入向量分别为ui∈Rd和uj∈Rd,其中d表示数据源嵌入向量的维度,ui和uj分别表示数据源si和sj的可靠度。
首先,定义数据源的联合概率qij如式(1)所示:
(1)
其中,dis(ui,uj) 表示嵌入向量ui与uj规范化后的余弦距离,用式(2)计算:
(2)
联合概率qij越大,则数据源si和sj的可靠度越相似,qij服从伯努利分布,数据源si和sj提供相同观测值的概率为qij,提供不同观测值的概率为1-qij。然后,定义nij为数据源si和sj提供相同观测值的个数,在给定联合概率qij条件下,产生nij的条件概率如式(3)所示:
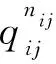
(3)
通过最大化条件概率,可靠度相似的数据源将在嵌入空间接近,最终定义“数据源-数据源”损失函数LSS如式(4)所示:
(4)
LSS损失函数衡量数据源的实际可靠度与其所在嵌入空间中的位置是否一致,LSS越小,则数据源可靠度编码越准确。
4.1.2 “数据源-观测值”损失
基于可靠数据源更可能提供可信观测值,不可靠数据源更可能提供错误观测值的假设,设计“数据源-观测值”损失,对观测值进行编码。设观测值cik的嵌入向量为vik∈Rd,表示对象ei的观测值cik的可信度,d表示观测值向量的维度,与数据源向量维度相同。
首先,对于对象ei,定义观测值cik由数据源sj提供的条件概率如式(5)所示:
(5)
其中,dis(vik,uj)表示嵌入向量vik与uj规范化后的余弦距离,嵌入向量vik与uj越相似,则其值越小,用式(6)计算:
(6)
p(cik|sj)服从多项式分布,其分母包含对象ei的全部观测值,能够模拟从数据源集合S中产生对象观测值的过程,符合真值发现观测值间可能存在冲突的特性。另一方面,p(cik|sj)越大,观测值cik和数据源sj的嵌入向量越相似,与假设可靠数据源通常提供可信观测值,不可靠数据源经常提供低可信度观测值的假设一致。
通过最大化条件概率,使可靠的数据源与可信观测值在嵌入空间接近(反之,不可靠的数据源与不可信的观测值在嵌入空间远离),最终定义“数据源-观测值”损失函数LSC如式(7)所示:
(7)


(8)
LSC损失函数衡量观测值可信度与其数据源可靠度是否一致,LSC越小,观测值可信度编码越准确。
4.1.3 双损失编码网络
结合“数据源-数据源”损失和“数据源-观测值”损失双损失,网络模型最终损失函数如式(9)所示:
L=LSS+LSC
(9)
基于式(9),设计如图2所示的双路双损失神经网络分别对数据源与观测值进行编码。整个编码网络由3部分构成:第1层为输入层,对数据源与观测值编码进行初始化输入;第2层为编码层,利用前馈神经网络对数据源可靠度与观测值可信度进行编码;第3层为输出层,输出嵌入空间编码和相似度矩阵。
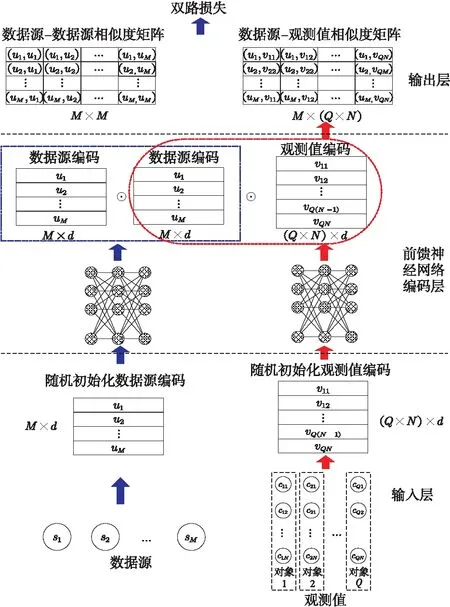
Figure 2 Illustration of proposed model图2 模型框架示意图
(1)第1层。该层为输入层,数据源编码网络输入样本为M×d的输入矩阵,其中M表示数据源数量,d表示数据源可靠度向量的维度;观测值编码网络输入样本为(Q×M)×d的输入矩阵,其中Q表示样本数量,d表示观测值可信度向量的维度。
(2)第2层。该层为编码层,主要是对数据源可靠度向量与观测值可信度向量进行编码,构造用于真值发现的数据源观测值嵌入空间。该层与输入层进行连接,并且前后都是全连接。编码层第1个隐含层的节点个数为d。
(3)第3层。该层为输出层,节点个数为d。数据源编码网络输出样本为M×d的输出矩阵,得到“数据源-数据源”相似度矩阵。对于观测值编码,将其输出与数据源编码网络的输出矩阵计算得到“数据源-观测值”相似度矩阵。
最后综合数据源编码网络与观测值编码网络的输出,利用式(9)计算编码损失,对双路前馈神经网络的参数进行优化,得到最终的数据源观测值嵌入空间。
4.1.4 双损失编码网络的学习过程
神经网络编码层的训练过程采用的是反向传播算法。输入原始数据即数据源可靠度与观测值可信度初始化向量,通过双路神经网络先各自前向计算各神经元的激活值,得到数据源可靠度编码与观测值可信度编码,然后综合2路编码信息,反向计算双损失;同时对误差求各个权值和偏置的梯度,并据此调整前馈神经网络中各个权值和偏差,得到最终的数据源可靠度与观测值可信度嵌入空间。

(10)
其中,ReLU(Rectified Linear Unit)是修正线性单元激活函数,能够将非线性特性引入到编码网络中,同时有效防止梯度弥散,提升收敛速度。
在网络的训练过程中,使用全部的观测值作为训练数据,无监督训练网络参数,得到最终的嵌入空间。
4.2 基于嵌入空间的真值发现
通过双损失神经网络编码,将数据源与观测值嵌入到高维空间,嵌入向量分别代表数据源可靠度与观测值可信度,同时可靠度相似的数据源与可信度相似的观测值在嵌入空间接近。通过投票机制,选择得票数最高的观测值对应的多个嵌入向量的均值作为“参考真值”向量,如对于对象ei,其参考真值v′i*由式(11)计算得到:
(11)
其中,vir(i=1,2,…,L)表示通过投票机制产生的最高票数观测值对应的多个嵌入向量,L表示提供该值的数据源的个数。本文定义该对象真值为距离“参考真值”最近的观测值,如式(12)所示:
vi*=arg mink(dis(vik,v′i*))
(12)
与简单投票不同,TDNNE将数据源可靠度估计与真值发现过程相结合,以嵌入空间为基础,将数据源间的相似度编码为数据源相对可靠度,提高真值发现过程的准确性。
5 实验与结果分析
本节通过在真实数据集上进行实验,验证TDNNE方法的有效性与准确性。首先,将本文所提方法TDNNE与传统真值发现方法及基于神经网络的真值发现方法进行对比,验证该方法的有效性和优越性。然后,研究学习率对所提方法的影响。最后对嵌入空间进行可视化,直观展示编码产生的数据源可靠度与观测值可信度。
5.1 实验设置
本文使用TensorFlow框架实现网络并进行训练,CPU为Intel Xeon E5-2630,内存为192 GB,GPU为NVIDIA Tesla P40×2,采用CentOS 7 64位操作系统。
5.2 实验数据
本文在真实数据集Weather和Flight(http://da.qcri.org/dafna/#/dafna/exp_sections/realworldDS/book.html)上进行对比实验,数据集来源于DAFNA(Data Forensics with Analytics),该网站为真值发现研究提供相关经典数据集,数据集的统计信息如表3所示。

Table 3 Statistical information of datasets表3 数据集的统计信息
Weather数据集:包含了16个网站关于不同地点不同时间的天气信息,包括温度(Temperature)、体感温度(Real Feel)、湿度(Humidity)、气压(Pressure)和能见度(Visibility)5个属性,该数据集提供了各个对象的真值。利用本文方法从多个网站提供的冲突信息中找到各个地区每天天气的真值。对于数据集中的空值,采用投票的方法进行填充。
Flight数据集:包含了38个不同网站提供的不同航班信息,包括实际出发时间(Actual Departure Time)、实际到达时间(Actual Arrival Time)、登机口(Departure Gate)、预计出发时间(Expected Departure Time)和预计到达时间(Expected Arrival Time)5个属性,该数据集提供了2011年12月~2012年1月的航班信息真值。利用本文方法从多个网站提供的冲突航班信息中找到各个航班的真实信息。对于数据集中的空值,同样采用投票的方法进行填充。
5.3 评价指标
本文采用自定义指标准确率(Pre)评价最终结果,其计算方式如式(13)所示:
(13)
其中,P为观测值真值总数量,TP为方法得到的正确观测值真值数量。准确率越高,真值发现方法效果越好。
5.4 对比方法与参数设置
本文将所提方法与多个真值发现方法进行对比,分别是基于迭代的真值发现方法Depen[7]、Accu[7]和AccuSim[7];基于概率图模型的真值发现方法Cosine[16]和3-Estimates[16];基于优化的真值发现方法CRH(Conflict Resolution on Heterogeneous data)[9];基于神经网络的真值发现方法FFMN(Feed Forward Memory Network)[21]。各个对比方法介绍如下:
(1)Depen:该方法考虑真值发现中数据源之间的复制情况,若2个数据源提供大量公共值,并且大部分的公共值很少由其他数据源提供,则很可能该数据源间存在复制行为。该方法使用贝叶斯分析来确定数据源之间的依赖关系,并设计一种迭代方法检测数据源之间的依赖,同时从冲突信息中发现真值,是一种可拓展的真值发现方法。Depen是Accu和AccuSim的核心方法。
(2)Accu:该方法优化了数据源间复制情况的准确度判定条件,计算特定对象的底层数据中观测值的概率分布,选择具有最高概率的值作为真值,是Depen方法的拓展。
(3)AccuSim:该方法针对枚举型数据进行真值发现。考虑观测值间的相似性,采用文献[4]提出的相似度度量模型,该方法是Accu方法的拓展。
(4)Cosine:该方法基于概率图模型,综合考虑Web数据中真值与观测值间的相关性估计数据源可靠度与观测值的可信度。使用余弦函数[35]对观测值相似度进行度量,并通过迭代的方法使其收敛。
(5)3-Estimates:该方法针对单真值发现问题,假设同一对象有且仅有一个真值。基于投票的方法,综合考虑每个对象的真值的可信度进行真值发现,是Cosine方法的拓展。
(6)CRH:该方法利用各种损失函数和正则化函数来描述不同的数据类型和权重分布,基于真值发现的假设设计目标函数,具有较高的收敛率和准确率,相较于其他真值发现方法准确率更高,是目前较优的非神经网络真值发现方法。
(7)FFMN:该方法基于对象的真值情况应该尽可能与各数据源提供的观测值接近,同时根据数据源的质量越高则其提供的对象属性集合与真值集合越相似的假设设计损失函数,将数据源与观测值之间的关系依赖利用前馈神经网络进行学习,将真值发现任务抽象为分类任务进行求解。
TDNNE使用Weather数据集全部数据源及其观测值进行编码,不进行训练集与测试集的划分,当模型连续500次迭代损失函数不发生变化时,停止迭代,得到数据源观测值嵌入空间,并进行真值发现。
5.5 实验结果
5.5.1 实验结果对比
表4和表5分别列出了TDNNE以及不同真值发现方法在数据集Weather和Flight上的对比实验结果。
由表4和表5可以看出,TDNNE真值发现方法优于基于迭代、优化及概率图模型的真值发现方法以及最新提出的基于神经网络的真值发现方法FFMN。CRH和FFMN的性能相对稳定,而Accu和AccuSim在处理Flight数据集时的准确率较处理Weather数据集有明显的提升。
基于迭代、优化及概率图模型的真值发现方法
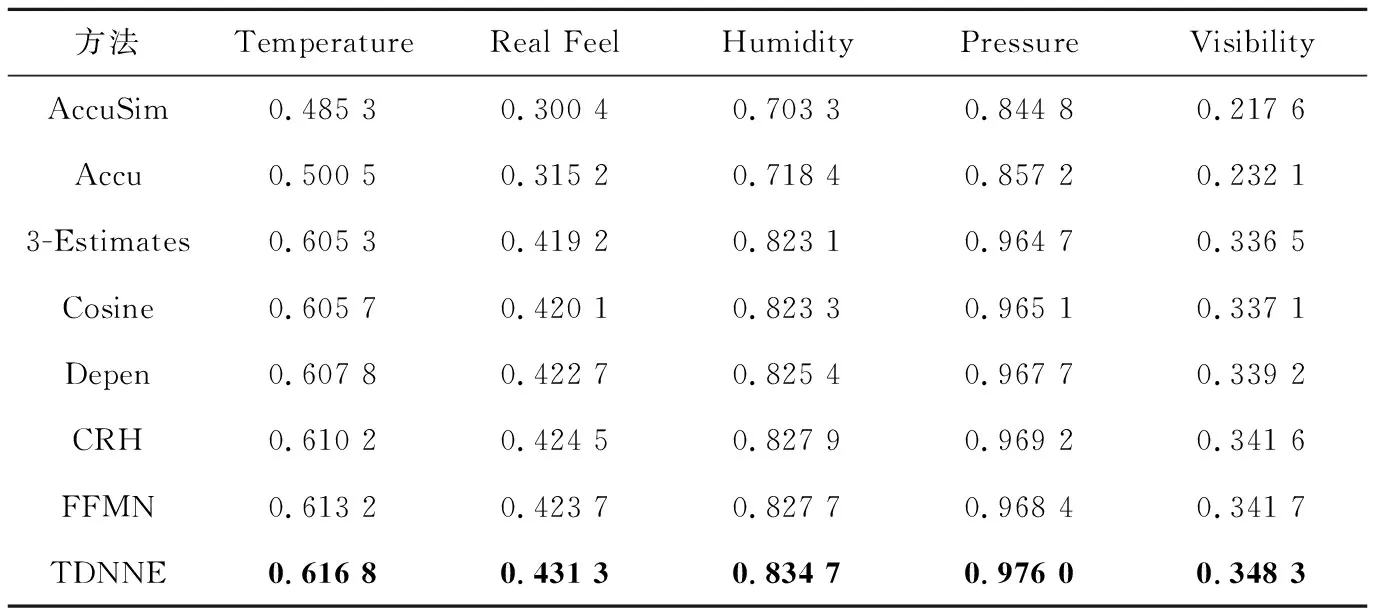
Table 4 Comparison of test results on Weather dataset表4 Weather数据集上的实验结果对比
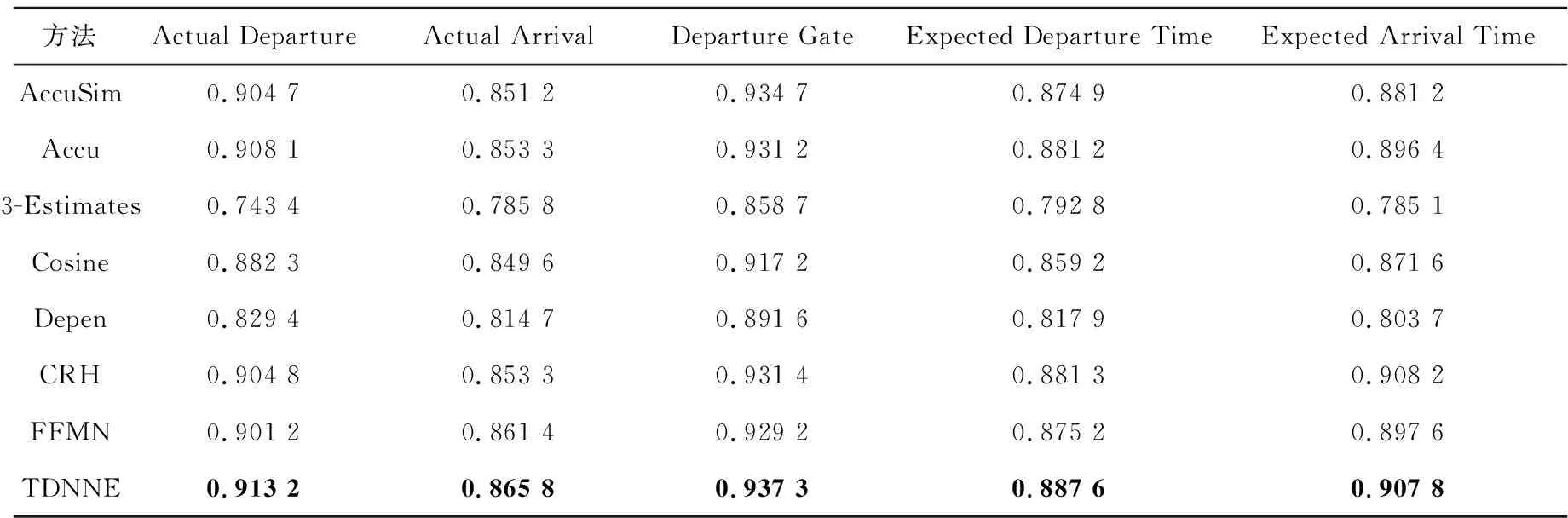
Table 5 Comparison of test results on Flight dataset表5 Flight数据集上的实验结果对比
由于人工假设数据源观测值间的依赖关系,难以真实反映数据的底层分布,导致真值发现结果不理想。而FFMN真值发现方法假设真值与大多数观测值相似,在特殊情况下其实并不适用,导致真值发现结果准确率不高。本文利用神经网络编码的思想来表示数据源可靠度与观测值可信度,一方面,高维空间表达能力更强,能更准确地描述数据源观测值间的关系依赖。另一方面,利用前馈神经网络将数据源与观测值嵌入到高维空间,不需要假设数据的分布,结果更准确。
5.5.2 学习率对实验结果的影响
在神经网络的优化过程中,学习率控制参数的更新速度,学习率过小,会极大降低收敛速度,可能陷入局部最优;而学习率过大,则可能导致参数在最优解两侧来回震荡,本节使用0.1,0.01,0.001,0.000 1,0.000 01进行实验,以验证学习率对实验结果的影响,结果如图3所示。

Figure 3 Influence of learning rate on experimental results图3 学习率对实验结果的影响

Figure 4 Encoding space of data sources图4 数据源编码空间
由图3可知,实验结果受学习率的影响较小,学习率为0.1和0.01时,实验结果相对较好。
5.5.3 编码空间可视化
5.5.3.1 数据源编码
为直观展示数据源编码操作的有效性,以Weather数据集的属性Temperature为例,对所有数据源以“数据源-数据源”损失进行编码,构造真实的数据源相似度矩阵,并对真实的数据源相似度矩阵与编码产生的数据源相似度矩阵进行可视化。
首先根据数据集标注等信息,计算出各数据源之间相同观测值的数量,以构造真实的数据源相似度矩阵。真实的数据源相似度矩阵构造方式如下所示:构造一个16×16的矩阵,1~16为数据源编号,矩阵的副对角线上的元素表示同一个数据源的相同观测值个数,所以副对角线的元素都为各数据源总观测值个数。除副对角线之外的其他元素值,表示对应2个坐标编号数据源之间的相同观测值个数,并以副对角线为对称轴对称。
图4a所示为16个数据源观测值相似度矩阵的真实分布,横纵坐标分别为数据源编号,图4a中给出了数据源之间相同观测值个数的情况。图4b~图4e所示为编码维度d分别为2,5,10,20时得到的数据源嵌入向量间的相似度矩阵,图4b~图4e中给出了最终数据源可靠度编码向量间的相似度。
首先,对比图4a与图4b~图4e可以看出,本文设计的网络及损失函数能够有效编码数据源,还原数据源间的相似度关系。将数据源嵌入到高维度空间后,嵌入空间的数据源相似度矩阵与数据源真实分布矩阵是一致的,即数据源的相似度关系与数据源间相同观测值比例关系保持一致。其次,对比图4b和图4c可以看出,数据源编码维度会影响实验结果,随着数据源维度增加,嵌入空间与真实分布逐渐相似,当维度d为20时,图4a与图4e几乎一致,此时数据源嵌入有效还原了数据源间的相似度关系。由此可见,相比实数,高维向量能够更好地表征数据源的可靠度。
最后,为验证该嵌入方法是否能真正反映数据源的可靠度,根据数据集提供的标准真值,对不同的数据源的真实准确率进行了计算。以准确率最高的数据源s14(Pre= 0.77)为例,由图4e可知,在嵌入空间,与其可靠度相似度高的数据源为s8(Pre= 0.63)和s10(Pre= 0.57);相似度相对较高的数据源为s3(Pre= 0.37)、s7(Pre= 0.43)、s11(Pre= 0.42)和s15(Pre= 0.47)等;相似度极低的数据源为s1(Pre= 0.34)、s5(Pre= 0.19)和s12(Pre= 0.23)。可见,数据源间的相似度与其实际真实准确率的相似度是基本一致的。同时,数据源s5与所有数据源在编码空间的相似度均较低,所以在嵌入空间,数据源s5的可靠度明显区别于其他数据源(表现为与其他所有数据源相似度均较低)。所以,通过数据源编码,准确率相似的数据源在编码空间距离上也逐渐接近,本文提出的数据源嵌入方法能够使可靠的数据源在嵌入空间彼此接近,并与不可靠的数据源远离。
5.5.3.2 观测值编码
为直观展示观测值编码的有效性,以Weather数据集的Temperature属性为例,对所有观测值以“数据源-观测值”损失进行编码,从准确率排名前3及后3的数据源中随机抽取200个观测值,使用T-分布领域嵌入T-SNE(T-distributed Stochastic Neighbor Embedding)[36]方法由20维降维至2维,并对其嵌入空间进行可视化。T-SNE方法将嵌入向量间的相似度转化为概率,将数据映射至高维空间后,嵌入向量间的相似性同时在高维空间表现出来,是目前较好的非线性数据降维与可视化方法。结果如图5所示。

Figure 5 Encoding space of claims图5 观测值编码空间
图5中,各点分别代表观测值经T-SNE方法降维后在二维空间中的位置,图中聚拢的不同簇表示不同数据源产生的观测值。由图5可知,通过观测值编码网络,各数据源提供的观测值向各数据源中心聚拢,在嵌入空间分成不同的簇。同时,观测值嵌入空间被大致分为3个部分,准确率相似的数据源在嵌入空间也相对接近。同时数据源相似度越高,则其距离也越近。经过编码得到的嵌入空间符合可靠数据源更可能提供可信观测值,经常提供相同观测值的数据源具备相似可靠度的假设。
6 结束语
针对传统真值发现方法简单假设数据分布与数据源观测值关系依赖,导致真值发现结果不理想的问题,提出了基于深度神经网络编码的真值发现方法。首先,考虑数据源与观测值间的关系,设计“数据源-数据源”“数据源-观测值”双损失;然后,利用双路前馈神经网络将数据源可靠度与观测值可信度嵌入到高维向量空间,相比实数,更准确地表达了数据源可靠度与观测值可信度;最后,基于投票机制设计基于嵌入空间的真值发现方法。真值发现过程不需要人工定义迭代规则,前馈神经网络自动学习其复杂的关系。在真实数据集上的实验结果表明,较传统真值发现方法,本文所提方法准确率更高,同时可视化分析也直观展示了数据源观测值的编码结果。
在下一步研究工作中,将会考虑更复杂的情况,提出更健全的损失函数,以提高真值发现的准确性,包括数据源之间的复制、数据的长尾效应等。

