驼峰堰堰后收缩断面水深计算的研究
王 功
(山西水利建设开发咨询有限公司 山西太原030002)
0 引言
溢流坝过流时,水流自坝顶下泄过程中,势能逐渐转化为动能,流速增加,沿下游坝面水深逐渐减小,最后在坝脚处必然有一最小水深断面,该断面称为水流收缩断面,其水深以符号hc表示,hc小于临界水深,由公式(1)可以计算求解[1]。

式中:E0——以收缩断面底部为基准面的坝前水流总比能;
hc——收缩断面水深;
Q——断面过流流量;
Φ——流速系数;
g——重力加速度;
Ac——收缩断面处过流断面面积。
由于Ac是hc的一次函数,显然公式(1)是收缩断面水深hc的三次方程。通过求解公式(1),可以求出hc的精确解。在工程设计中,常常用试算法来求解。公式(1)中hc的解有三个根,通常符合实际情况的解是小于临界水深的那个根,所以试算时可只在小于临界水深的数值中选取hc的数值[2],经过多次试算,即可求出正确的解。
1 问题的提出
1.1 算例
某水利枢纽工程溢洪道全长191.63 m,由进水段、控制段、泄槽段、挑流段四部分组成。进水段纵坡为平底;控制段为矩形,净宽12 m,长度10.4 m,底板设置驼峰堰来控制水流,堰高1.30 m;泄槽段由两段组成,上游段纵坡为0.75%,下游段纵坡为9%,泄槽断面为矩形断面,净宽12 m,全断面混凝土衬砌;挑流消能段全部采用C25 混凝土浇筑。溢洪道设计泄量为322 m3/s,根据堰流公式,计算得总水头Ho为5.75 m,堰顶水头H 约为4.66 m;根据临界水深、临界底坡计算公式,计算得出泄槽的临界水深为4.188 m,临界底坡为0.49%;泄槽上游段纵坡0.75%,正常水深是3.22 m;下游段纵坡9%,正常水深是1.40 m。溢洪道纵剖图见图1,控制段驼峰堰的横剖图见图2。

图1 溢洪道纵剖图
现在我们来求该溢洪道在泄量为322 m3/s 时的驼峰堰堰后水深。常规的算法如下:
考虑坝前行进流速,把各已知数据:E0=7.05 m,Q=322 m2/s,令Φ=1 代入公式(1)得三次方程:

解方程得:hc1=6.05 m,hc2=3.02 m,hc3=-2.01 m。由于该数值小于0,不符合工程实际情况,显而易见被排除掉。在hc1和hc2之间按通常的计算经验,在二者之间取小于临界水深的值,本例溢洪道的临界水深为4.188 m,自然我们就会选取hc2=3.02 m 的值作为本例的解。那么,我们所求的解是否符合实际情况呢?下面我们将进一步深入分析和探讨。
1.2 分析研究
1.2.1 与实际情况比较分析
从上文我们可知,如果按通常的计算原则取小于临界水深的值,本例计算结果取hc2=3.02 m 的解。但我们从图2 中可以看到,驼峰堰高出河床1.3 m,而堰上水头为4.66 m,堰顶高程至与泄槽衔接处水平距离仅5.2 m,驼峰堰高度仅1.3 m,水流不可能像在高坝表面上那样沿堰面充分流动从而在坝脚处形成收缩断面;也就是说该驼峰堰堰后水深在短距离、低堰的情况下,没有充分的能量使水深小于正常水深3.22 m,从而形成图3 所示的水面线3 的情况。

图2 驼峰堰横剖图
1.2.2 理论分析
根据棱柱体恒定非均匀流渐变流的水面线原理,将溢洪道泄槽可能水面线型式作图如下(见图3)及分析见表1。图中KK 线即为临界水深hk的水位线,NN线即为正常水深ho的水位线。水面线1、2、3、4 即为本例堰后溢洪道泄槽可能的水面线,根据有关参考资料[3],本例泄槽水面曲线a、b、c 区详细情况见表1。

图3 溢洪道泄槽水面线

表1 溢洪道泄槽水面线分析
从图3 及表1 分析,本例中溢洪道的水面线应为水面线2 和4 的组合或者是水面线3 和4 的组合。最终确定为哪一组合水面线,是由上游控制水位决定的,也就说是由驼峰堰堰后水深决定的。从实际情况分析,上游没有闸门控制,堰后水深不应该在c 区,在b 区的可能性更符合实际情况。而应用公式(1)计算的结果来看,水面线反而在c 区,公式(1)是应用能量定理推断出来的,公式无疑是正确的。那么问题出现在哪里呢?
2 计算研究及合理选取计算值
进一步分析判断,可得知上述在用公式(1)计算堰后水深时,唯一可能出现误差的就是公式中流速系数Φ=1 的选取上可能出现了失误。造成计算结果和实际情况不相符的状况。下面我们将从公式中的流速系数Φ 值的选取及相关参数取值的范围展开研究和讨论。
根据有关资料[1],公式(1)是根据能量方程式推出来的,公式原本为:


式中:αc——动能修正系数;
ζc——断面间水头损失系数;
其他符合意义同公式(1)。
流速系数Φ 是关于αc和ζc的函数,根据有关资料[4],我们知道αc值为动能修正系数,其值大小取决于过水断面上流速分布情况,流速分布愈均匀,αc愈接近于1;不均匀分布时,αc>1;在渐变流时,一般为1.05~1.1 之间;在本算例中,αc定位于渐变流的情况。
参数ζc表示的是断面间水头损失系数,在没有水力模型试验的情况下,只能由设计人员根据自身的工程经验结合Φ 值参考的取值范围[1],通过公式(1)来计算,从而避免了直接对参数ζc的直接选取。
综上所述,本例题的计算中流速系数Φ 的选取值为1 是不合适的。关于Φ 值的数值选取,水力学计算有关书籍[5]也未列出驼峰堰的类型,为进一步深入研究,我们下面将通过选取不同的Φ 值,再次用公式(1)计算本例题的hc值。代入题中各已知数据,得出计算式如下:

取不同的Φ 值计算如表2 所列。
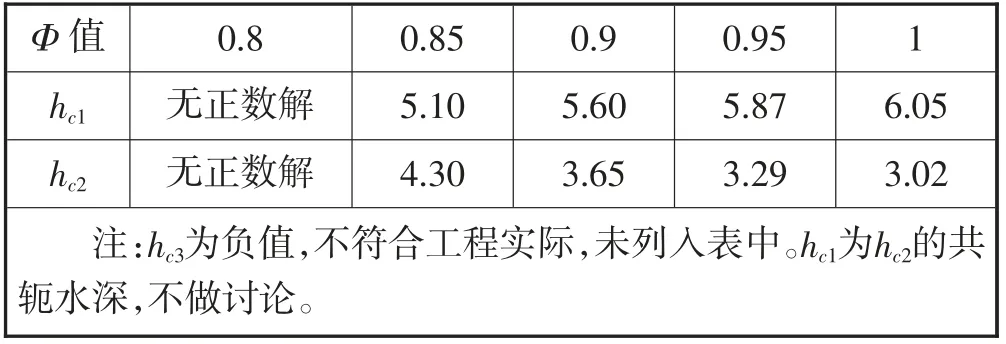
表2 不同Φ 值计算的堰后水深值(较小值)比较表
当Φ=0.8 时,hc1,hc2无正数解,可解释为:当Φ=0.8 时,⇒αc+ζc=1.56,又因为本例中:αc=1.05~1.1,推断出参数取值ζc较大所致,即物理意义为断面间水头损失估计偏大,导致堰后水深计算无正数解,不符合本例题的情况。
当Φ=1 时,hc2=3.02 m⇒αc+ζc=1,又因为通常:αc≥1,得出:ζc=0,即物理意义为断面间水头损失为零(此种状况理解为断面间水头损失很小,此时忽略断面间水头损失,不影响计算结果,可令Φ=1 计算,即为工程设计中的常规算法)。从图3 和表1 中水面线的原理分析可知,若hc2=3.02 m,水面线在c 区,属于上游有闸门控制的情况,不符合本算例的情况。所以,hc2=3.02 m 计算的结果不能采纳。
当Φ=0.85、0.9 或0.95 时,其中hc2的值分别为:4.30、3.65、3.29,由于值4.30 大于临界水深,由图3 可知不符合算例的水面线原理。其余两个解无论哪个值都间于纵坡为0.75%泄槽的临界水深4.188 m 和正常水深3.22 m 之间。所以,当Φ=0.9 或0.95 时,计算得出hc2=3.65 m 或3.29 m 都是合理的解。因此,可以确定本例中溢洪道的水面线最终为水面线2 和4 的组合。对于本例题可取3.65 m 的计算结果,保证工程设计运行安全。若要更精确的选取计算结果,需要通过做水力模型试验具体确定工程中合理的Φ 值代入公式计算可获得。
综上所述,本例题的正确解可取Φ=0.9,hc2=3.65 m。
如果按照例题开始的常规算法求解,令Φ 值为1,计算得出:hc2=3.02 m,则溢洪道泄槽的水面线最终为水面线3 和4 的组合(见图3)。由于泄槽纵坡为0.75%的上游段水面线2 和3 是分布在b 区和c 区的,他们有本质的区别的(见表1)。
综上所述,和本例题类型相近的驼峰堰堰泄流工程,运用水面线原理结合取不同值计算,经分析选取合理的堰后水深的计算方法是合理可行的。
3 结论与建议
综上所述,公式(1)在Φ=1 的时候,适用于高溢流坝泄水下游收缩断面水深的计算,特别是对于堰上水头明显低于坝高的情况。如图4 所示,由于H 远小于P,水流可以充分沿着坝面流动,流速增加,水深逐渐减小,最终在坝脚处达到最小值hc;在断面间的水头损失只有沿程损失,相对占比很小,可以忽略不计;此种情况,令系数Φ=1 计算造成的误差不足以影响计算结果。
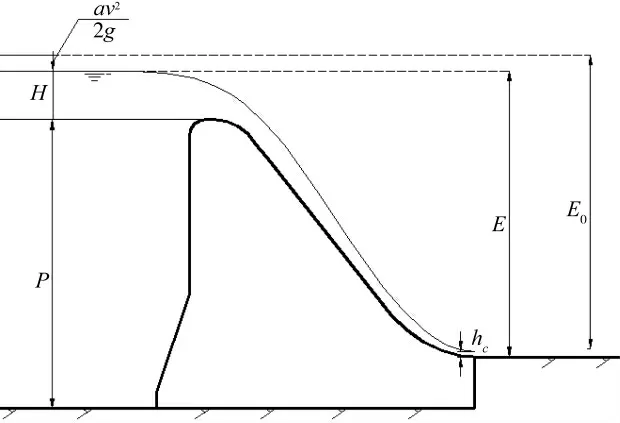
图4 高溢流坝过水示意图
而如图2 所示的驼峰堰堰上水头远大于坝高,过坝水头不可能像在高坝那样可以在堰面上充分流动形成类似于高坝下游的收缩断面的水流状况,此时,相对而言,断面间的水头损失相对占比很大,不可以忽略,仍按通常取Φ 值为1(如上所述,此种状况物理意义为断面间水头损失为零)用公式(1)计算是不合适的。如果不详细分析系数Φ 值的选取,该系数在选取上造成的误差足以影响计算成果,就会选出不符合实际情况的计算成果,遇到该类问题应该像本文算例研究的方法一样详细分析系数Φ 值不同的取值,结合水面线原理,合理确定出驼峰堰后的水深值。在水利工程设计中应该引起设计人员的高度重视。

