基于DFA的地下厂房围岩稳定安全评价
尹彦礼 张建伟 马保宁 李伟 李香瑞


摘 要:为判断水电站地下厂房围岩的稳定情况,提出一种非趋势波动分析方法(Detrended Fluctuation Analysis,简称DFA),构建判断围岩变形趋势进而判断其稳定性的判据。根据某抽水蓄能电站厂房围岩变形监测数据,将时间序列按周期划分,再利用非趋势波动分析方法从整体和分段两方面判断围岩变形趋势,作为水电站厂房设计规范的辅助判据,分析围岩的稳定性,并与突变理论判断围岩稳定性作对比验证。研究表明:该水电站地下厂房处于稳定状态,方法合理有效,且累积时段的分析结果规律性更强,与匀时段有明显差异,即分析方式对结果存在一定影响。
关键词:围岩;稳定;变形趋势;安全评价
中图分类号:TV731.6
文献标志码:A
doi:10.3969/j.issn.1000-1379.2021.09.025
引用格式:尹彦礼,张建伟,马保宁,等.基于DFA的地下厂房围岩稳定安全评价[J].人民黄河,2021,43(9):129-132,138.
Safety Evaluation of Surrounding Rock Stability of Underground Powerhouse Based on DFA
YIN Yanli1, ZHANG Jiangwei1, MA Baoning1, LI Wei2, LI Xiangrui1
(1.North China University of Water Resources and Electric Power, Zhengzhou 450046, China;
2.Nanyang River Affairs Office, Nanyang 473000, China)
Abstract: In order to judge the stability of surrounding rock of underground powerhouse of hydropower station, a detrend fluctuation analysis method (DFA) was proposed to construct a criterion to judge the deformation trend of surrounding rock and then to judge its stability. According to the deformation monitoring data of surrounding rock of a pumped storage power station, the time series were divided into periods, and then the deformation trend of surrounding rock displacement time series and rate time series was judged by non trend fluctuation analysis method from the whole and subsection aspects. As the Auxiliary Criterion of Hydropower Station Powerhouse Design Specification, the stability of surrounding rock was analyzed and compared with catastrophe theory. The research result shows that the underground powerhouse of the hydropower station is in a stable state, the method is reasonable and effective, and the analysis results of cumulative period are more regular and there are obvious differences compared with the uniform period, that is, the analysis method has a certain influence on the results.
Key words: surrounding rock; stability; deformation trend; safety evaluation
圍岩稳定性问题在地下岩土工程的合理设计和安全运行中起关键作用,岩体行为复杂,影响围岩稳定性的因素众多,目前尚无受到广泛认可的地下洞室围岩稳定性判据,因此围岩稳定性及变形研究一直是热点[1-3]。近年来,国内外许多学者对围岩变形趋势及稳定性评价方法进行研究,取得了丰富的成果[4-8]。杨云浩等[9]通过应变软化模型研究了地下厂房围岩的变形破坏原理;YUAN等[10]研究了节理岩体边坡在地震影响下的安全系数;李仲奎等[11]进行了三维地质力学模型试验,从全局上分析地下洞室工程整体力学特征、变形趋势和稳定性特点。上述对围岩的研究方法有其各自的适用性,也存在一定的局限性。对于数值模拟方法,其最主要表现为不具备普适性;而室内外试验方法虽然更接近于工程实际,但往往费时费力,实用价值有限。这些问题,也是当前地下洞室围岩稳定性研究中亟待解决的问题。
非趋势波动分析(Detrended Fluctuation Analysis,简称DFA)能对评价序列的趋势性进行有效判别。C.Castillo-Botón等[12]基于DFA对水库水位进行了长期和短期的分析及预测;Pavlov等[13]基于DFA通过比例指数的变化考虑时变非平稳行为的特征。
监测位移能够有效地反映围岩的变形情况,通过对监测位移的处理和分析能够有效地获取围岩动力学特性,考虑到非趋势波动分析对数据良好的趋势性评价,从而对围岩稳定性进行可靠的安全评价。现有的围岩稳定性判别理论,大都基于个别工程自身特点,进行建模或试验分析。这样的方法虽然具有较高正确性,但也使得其缺少普遍适用性。为此,笔者提出了基于监测数据的围岩稳定性DFA判定方法,结合现行水电站地下厂房设计规范[14],得到一种具有普遍参考价值的判断围岩变形趋势从而判断其稳定状态的方法,并与尖点突变理论计算结果分析对比,验证DFA方法评价围岩稳定性的可行性;同时从整体和分时段两种不同角度综合分析围岩稳定性,为围岩稳定性判别提供新的思路。
1 非趋势波动分析理论
非趋势波动分析是一种标度指数计算方法[15],其具體步骤如下。
(1)累积离差计算。设非平稳时间序列为{zp|p=1,2,…,n},则第i个节点的累积离差G(i)为
G(i)=∑it=1(zt-z-)(1)
式中:z-为时间序列均值。
(2)序列重构。将新得到的序列G(i)等分为Ns个不重叠的区间,每个区间的长度为s。
Ns=n/s(2)
通常来说,n不一定能被s整除,原序列最后一些数据可能未被使用。为了充分利用数据,再从最后一个数据开始,逆序划分Ns个不重叠的区间,共计2Ns个子区间。s一般根据经验取值,n/4≥s≥q+2,其中q为波动函数的阶数[16]。
(3)对每一个数据区间采用最小二乘法进行拟合,并滤去趋势Pu(i),计算每段数据的方差F2(v,s):
F2(v,s)=∑si=1{G[(v-1)s+i]-
Pu(i)}2/s (v=1,2,…,Ns)(3)
F2(v,s)=∑si=1{G[n-(v-Ns)s+i]-
Pu(i)}2/s (v=Ns+1,Ns+2,…,2Ns)(4)
(4)计算序列的q阶波动函数,并求各子序列方差的均值:
Fq(s)=q12Ns∑2Nsv=1[F2(v,s)]q2(5)
标准DFA的波动函数q值取2[17],则式(5)变为
Fq(s)=12Ns∑2Nsv=1F2(v,s)(6)
(5)求解α(标度指数)。先取子区间长度s,得到若干散点[s,F(s)],各散点之间为幂相关,这里s选取区间q+2,n/4中整数值。然后对各点进行对数处理,将双对数坐标按最小二乘法进行直线拟合,由此求出直线的斜率。
lg s=∑n/4i=q+2lg si(7)
lg F(s)=∑n/4i=q+2lg F(si)(8)
令a=∑n/4i=q+2lg silg F(si),b=n/4-(q+2),c=lg s×lg F(s),d=∑n/4i=q+2(lg si)2,e=(lg s)2,则α表示为
α=a-bcd-be(9)
当0.5<α<1.0时,序列相关趋势呈现的持续性为正,即后一阶段与前一阶段的发展趋势相同,且α值越大,序列趋势性越强;当α=0.5时,序列随机,且是一个独立的过程,此时不能对其发展趋势作出判断;当0<α<0.5时,序列相关趋势呈现的持续性为负,即后一阶段与前一阶段的发展趋势相反,且α值越小,序列趋势性越强。
分别通过对围岩的位移和速率求α值,比较其大小,判断围岩变形是否收敛。
2 工程实例
2.1 工程概况
某抽水蓄能电站地下厂房系统布置在右岸横岭山体内,厂房长180.0 m、宽24.5 m、高52.3 m,具有高边墙、大跨度的特点。由于水库的存在,岩体中裂隙水压力偏高,降低了岩体的物理力学性质,因此对工程的安全稳定运行产生了一定威胁。为观测其状态,在主厂房和主变洞布置了5个监测断面(如图1所示),分别位于主厂房1#机、3#机、安装场以及1#主变、3#主变附近,均安装多点位移计、渗压计和锚杆应力计。
围岩内部(顶拱、左侧壁和右侧壁)0、1.5、3.5、8.5 m处的绝对位移由所在位置的多点位移计测量得到,厂房多点位移计布置如图2所示,其中M1~M29为多点位移计测点编号。
根据实际情况,围岩变形由岩体内部向临空面方向逐渐增大,孔口处最危险,即孔口处的状态往往决定着整个锚杆附近的围岩是否处于稳定状态。对厂房围岩进行监测,其中I—I断面顶拱拱脚处一个测点M4的累积位移曲线如图3所示。监测序列共1 921 d,可分为64个周期,测点M4变形速率曲线如图4所示。
由图3可知,围岩整体变形极小,无明显突变,但累积位移仍有持续性增长趋势。分析可知,围岩变形速率前期波动幅度较大,后期波动幅度较小,逐渐趋于0,此时锚杆刚度几乎不发生改变,即支护结构受力变化亦趋于0。
2.2 围岩变形稳定性分析
根据水电站地下厂房设计规范[15]可知,支护实施后位移增长速率趋于0(即围岩变形趋于收敛),支护结构的受力变化也趋于0(即围岩位移趋于0、支护结构刚度几乎不发生改变),可判断洞室处于稳定状态。再采用DFA方法对围岩稳定性作进一步判断。
2.2.1 围岩整体变形趋势分析
利用DFA方法和所有位移序列(共64个监测周期),对M4处围岩变形趋势进行整体性分析,并与变形速率序列的分析结果进行对比,见表1。
位移序列和变形速率序列均具有较好的拟合优度和均方误差,即具有较优秀的拟合效果,DFA分析围岩变形趋势性的可靠度较高;两个序列的α(标度指数)均处于0.5~1.0之间,且α位移>α变形速率,两个序列的变化趋势为持续增长,围岩M4处变形趋势收敛。
受篇幅所限,仅简列出I—I断面各测点DFA计算结果,见表2。
由表2可知,I—I断面各测点处于稳定状态,引入文献[18]中一种判定围岩稳定性的新准则——尖点突变理论,对各测点进行计算,验证表2计算结果。
以I—I断面顶拱处M4测点为例,将其监测数据进行整理,获取变形速率,再将反演得到的非线性动力模型积分可得
V=-2.263×10-1X4+1.772×10-1X3-
1.706×10-1X2-5.223×10-2X(10)
式中:V为位移;X为时间。
对式(10)进行Tschirnhaus变换,令X=Y-L,其中L=-0.195 8,则
V=d0+d1Y+d2Y2+d4Y4(11)
式中:Y為变换后的与时间有关的参数,参数d4、d2、d1、d0分别为-0.226 3、-0.118 6、-0.105 5、-0.012 7。
令P、Q、E分别为d2、d1、d0与d4的比值,P=0.523 9,Q=0.466 0,E=0.056 0。由判别式Δ=8P3+27Q2,可得Δ=7.01>0,说明测点M4附近区域处于稳定状态。
根据尖点突变理论,计算得到I—I断面测点M1~M9各参数及Δ,见表3。
由表3可知,各个测点位移尖点突变模型的判别式Δ均大于0,可判定I—I断面各测点处于稳定状态,与DFA分析结果一致。
2.2.2 围岩分时段趋势分析
匀时段分析和累积时段分析是分时段趋势分析的两种方式。匀时段分析是将整体位移序列或变形速率序列分为具有相同样本数的若干时段;累积时段则是取一定长度的时间序列进行分析,而后依次增加相同长度的时间序列共同分析,直到整个时间序列分析完整。
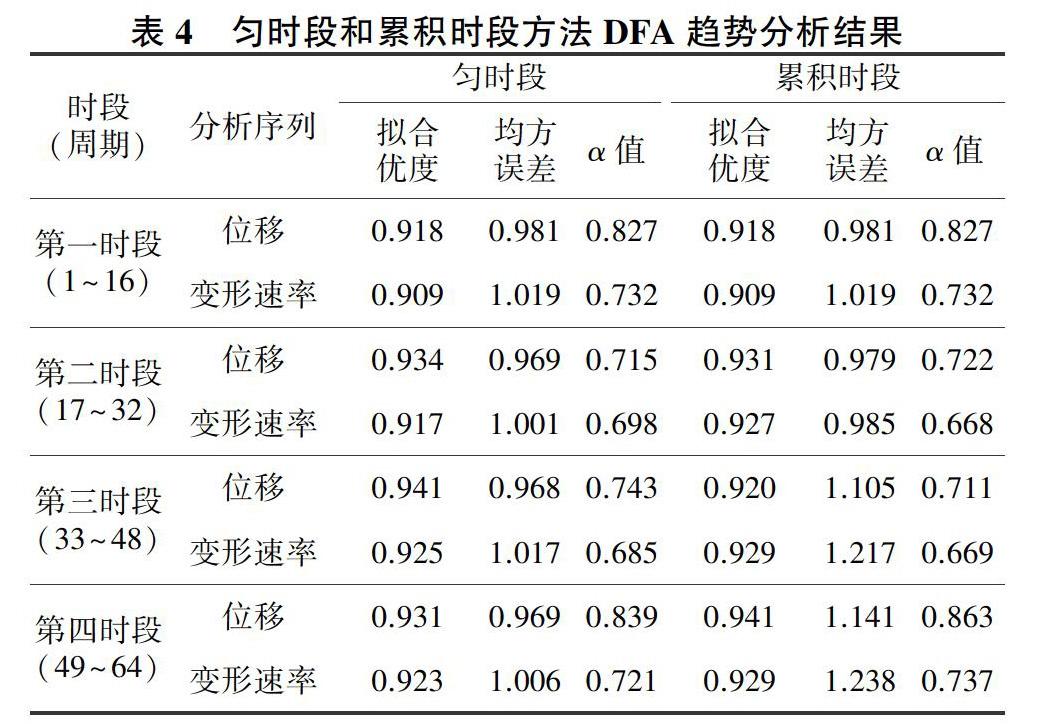
实际观测的时间序列以16个周期为1个时段,共4个时段,对两种不同的时段划分方法进行DFA分析对比,结果见表4。
由表4可知:①匀时段划分后,两种序列的拟合优度和均方误差较优,均具有较优的拟合效果;②各时段两个序列的α值互不相等且都处于0.5~1.0之间,说明两个序列的趋势为持续增长,且各个阶段变形程度存在差异;③α位移>α变形速率,说明与变形速率序列相比,位移序列的增长趋势性更强。同时,对于累积时段DFA趋势分析,其拟合优度、均方误差、α值(大于0.5)随着序列长度的增加存在不同的差异,但α位移>α变形速率,与匀时段分析结果一致,联合围岩变形速率曲线得到位移增长速率趋近于0,即围岩变形趋于收敛,判断测点M4区域围岩处于稳定状态。但是,在累积时段分析中,相较于时段2、3,时段1、4的α值更大。可见,两种时间序列分段方法分析判断围岩变形趋势结果一致,但是变形趋势的程度有差异。因此,可以运用分时段和整体性两种分析方法对围岩的变形趋势进行综合性分析,进而对围岩的稳定性进行评价。
3 结 论
围岩变形受外界环境和人为因素影响,是一种复杂的演化过程;通过分析围岩的累积位移和变形速率来分析围岩的稳定性是可行的。
采用DFA方法与现场实测数据相结合,得到围岩变形呈持续增长趋势,且累积位移序列趋势性强于变形速率序列,判断围岩处于稳定状态,与实际相吻合;与尖点突变理论计算结果进行了对比验证,分析结果可靠。
参考文献:
[1] 赵瑜,张建伟,院淑芳.基于突变理论的地下厂房围岩稳定性安全评价[J].岩石力学与工程学报,2014,33(增刊2):3973-3978.
[2] 刘武斌,郭乙霏,雷银拴.前坪水库泄洪洞施工期监测及围岩稳定分析[J].人民黄河,2019,41(7):140-142.
[3] 贾超,廉明远.蚀变岩体隧洞围岩变形响应模拟研究[J].人民黄河,2018,40(6):133-135.
[4] 张建伟,暴振磊,赵瑜,等.基于小波奇异性与突变理论的地下厂房围岩稳定性评价[J].水电能源科学,2015,33(9):106-109.
[5] 王洪建,赵龙翔,李瑾,等.层状巷道围岩稳定性的试验研究[J].华北水利水电大学学报(自然科学版),2019,40(2):90-96.
[6] 周家文,徐卫亚,石崇.基于3DEC的节理岩体边坡地震影响下的楔体稳定性分析[J].岩石力学与工程学报,2007,26(增刊1):3402-3409.
[7] LI Y, WANG H P, CAI W B, et al. Stability Monitoring of Surrounding Rock Mass on a Forked Tunnel Using both Strain Gauges and FBG Sensors[J]. Measurement,2020,153:1-10.
[8] 邹红英,梁成彦,吴昊.CCS水电站地下洞室群围岩稳定关键技术研究[J].人民黄河,2019,41(7):116-120,125.
[9] 杨云浩,王仁坤,邢万波,等.猴子岩水电站洞群硬脆性围岩变形破坏特征的3DEC分析[J].岩石力学与工程学报,2015,34(增刊2):4178-4186.
[10] YUAN H P, CHEN C H, HE Z M,et al. Numerical Simulation of Fluid-Solid Coupling in Surrounding Rock for River Stope Mining[J]. Shock and Vibration,2020,11(3):1-11.
[11] 李仲奎,卢达溶,中山元,等.三维模型试验新技术及其在大型地下洞群研究中的应用[J].岩石力学与工程学报,2003,22(9):1430-1436.
[12] CASTILLO-BOTN C,CASILLAS-PREZ D,CASANOVA-MATEO C,et al. Analysis and Prediction of Dammed Water Level in a Hydropower Reservoir Using Machine Learning and Persistence-Based Techniques[J]. Water,2020,12(6):1-22.
[13] PAVLOV A N,DUBROVSKY A I,KORONOVSKII A A,et al. Extended Detrended Fluctuation Analysis of Electroencephalograms Signals During Sleep and the Opening of the Blood-Brain Barrier[J]. Chaos (Woodbury, N.Y.),2020,30(7):1-10.
[14] 国家能源局.水电站地下厂房设计规范:NB/T 35090—2016[S].北京:中國电力出版社,2017:13-15.
[15] 周安康,严宝文.渭河流域月径流序列分形特征研究[J].水力发电学报,2014,33(4):7-13.
[16] 吴永恒.基于自适应非趋势波动分析的齿轮故障诊断[D].武汉:武汉科技大学,2014:22-24.
[17] 田成成,张盛生,张磊,等.基于尖点突变理论及非趋势波动分析的滑坡稳定性及变形特征研究[J].大地测量与地球动力学,2018,38(8):806-810.
[18] PENGY X, WU L, CHENC H,et al. Stability Analysis of Surrounding Rock in Tunnel Crossing Water-Rich Fault Based on Catastrophe Theory[J]. Geotechnical and Geological Engineering: an International Journal,2020,38(1):415-423.
【责任编辑 张华岩】

