改进邓肯-张模型及其在软岩填料中的应用
刘江波,刘凯,田军,刘晓明
(1.海口市市政工程设计研究院,海南 海口 570100;2.中交第二航务工程勘察设计院有限公司;3.湖南省张桑高速公路建设开发有限公司;4.湖南大学 土木工程学院)
自土力学建立以来,国内外研究者对土建立了众多各具特色的本构模型,基于偏应力-应变关系为双曲线形式假定推导得到的邓肯-张非线性弹性模型是其中的一个。虽然将土视为弹性材料不尽合理,但是由于邓肯-张双曲线模型具有物理意义明确,参数确定容易等优势,其应用的广泛程度反而超过许多理论严密的模型,是各种岩土工程商业数值分析软件必备的模型,对其进行持续研究和改进仍具有重要实用价值。罗刚、张嘎等针对邓肯-张对土体剪胀性描述不足方面进行改进;孔德志等则讨论了多种考虑中主应力影响的改进邓肯-张模型的合理性;沈启鹏等基于钙质结合土的应力应变特性,对邓肯-张进行修正;杨爱武、王立忠、王晓妮在改进模型中考虑了土体结构性的影响。
压实填土是道路、大坝等构筑物的主体,其变形对构筑物的正常工作具有重要意义,在压实填土的变形分析中,邓肯-张模型也得到了广泛应用。但是,三轴试验表明:与邓肯-张模型推导时所依据的正常固结土试验数据不同,压实填土或是因受到强力机械压实作用的原因,其(σ1-σ3)-ε1关系曲线形态与双曲线的符合程度随围压不同显现出不同差异:在高围压下接近双曲线,随围压降低逐渐偏离至差异显著。将邓肯-张模型直接应用在压实填土构筑物的数值分析中时,可导致填筑体体积应力小的部分(填筑体上部)变形计算结果不准确,而这部分正是填筑体直接承受外荷载作用的部分。
软岩填料属于典型压实填料,它是由大块软岩经人工重复破碎和压实而形成,其颗粒大小随重复破碎次数不同而不同。为了研究软岩填料变形和强度特性随颗粒粒径不同的变化规律,该文对最大粒径分别为2、10、20 mm软岩压实填料试样进行三轴试验,在试验中发现,粒径越大,试样击实到相同密度所用能量越大,而击实能量越大的试样(σ1-σ3)-ε1关系与双曲线差异也越大;另一方面,相同粒径条件下围压越小时(σ1-σ3)-ε1曲线形态与双曲线差异也越大。试验说明填料压实过程和围压对试验结果有重要影响,邓肯-张模型中并没有能反映该影响的参数。经过研究,该文在邓肯-张模型的基础上,加入一个能反映填料压实程度和围压大小的参数,改善(σ1-σ3)-ε1曲线形态与试验结果的符合程度,改进的模型不仅完全保留了邓肯-张模型意义明确、参数易于确定的优势,而且其更适用于压实填料,有望用于各类压实填土构筑物的变形数值分析中。
1 改进邓肯-张模型
1.1 邓肯-张E-B模型
邓肯-张E-B模型是在常规三轴试验结果上建立的,首先假定(σ1-σ3)-ε1满足双曲线关系,可用式(1)表示,并在此基础上推得切线模量Et的表达式如式(2),接着假定切线体积模量Bt与应力水平无关,仅随围压σ3而变,其关系满足式(3)。
(1)
(2)
(3)
式中:Et为切线模量;Bt为切线体积模量;pa为大气压;而内摩擦角φ、黏聚力c、破坏比Rf、K、n、Kb、m为邓肯-张(E-B)模型中的7个参数,可以由常规三轴试验得出。
1.2 模型曲线方程的改进
填土在压实过程中会受到强外力作用,可导致其(σ1-σ3)-ε1关系与双曲线出现差异,对多组典型压实填土的三轴试验结果进行分析,发现了如下规律:
(1)(σ1-σ3)-ε1曲线形态与围压相关,围压较高时与双曲线较接近,围压降低渐渐偏离双曲线至差异显著。
(2)在围压较低时的(σ1-σ3)-ε1曲线会出现明显的转折点,该点之前偏应力随轴向应变上升较快,之后接近水平。
为准确描述该变形规律,同时保留原始E-B模型的优点,在式(1)右边增加一项lε12[如式(4)所示,作者原创],曲线形态就可以得到调整(图1),其中:当l=0时,为双曲线;当l→∞时,曲线逼近双折线。
(4)
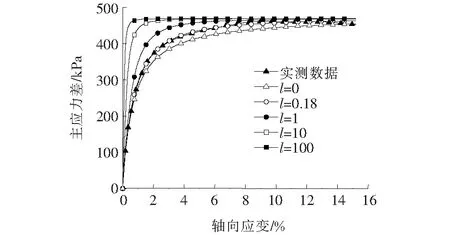
图1 l值对(σ1-σ3)-ε1曲线形态的影响
1.3 改进的邓肯-张模型
由于改变了(σ1-σ3)-ε1曲线方程,需在式(4)基础上重新推导切线模量Et的表达式。在常规三轴压缩试验中,由于dσ2=dσ3=0,所以根据式(4)可导得切线模量为:
(5)
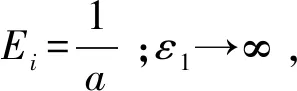
(6)
(7)
由式(4)变换,可以得到ε1的表达式:
(8)
将式(8)代入式(5)得到:
(9)
将式(6)和(7)式代入式(9)得到:
(10)
根据莫尔-库仑强度准则,有:
(11)
初始模量Ei与围压满足关系:
(12)
将式(11)、(12)代入式(10),得到:
(13)
其中:
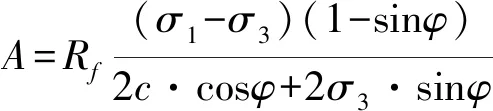
式(13)为改进邓肯-张模型切线模量的计算表达式,其中参数l是与填土压实过程及试验围压有关的参数,其确定方法和意义在下文分析。
2 软岩填料三轴试验曲线特征
2.1 试样制备
为了研究软岩填料变形和强度特性随颗粒粒径不同的变化规律,对最大粒径分别为2、10、20 mm填料试样进行了三轴试验。软岩填料基本性质为:岩块天然抗压强度为24.0 MPa;破碎后形成的填料,实测天然含水量为9%、现场压实后干密度为1.79 g/cm3。按现场级配进行缩尺,得到不同最大粒径的软岩缩尺填料,缩尺填料最大粒径dmax分别为2、10、20 mm,实测级配曲线如图2所示。
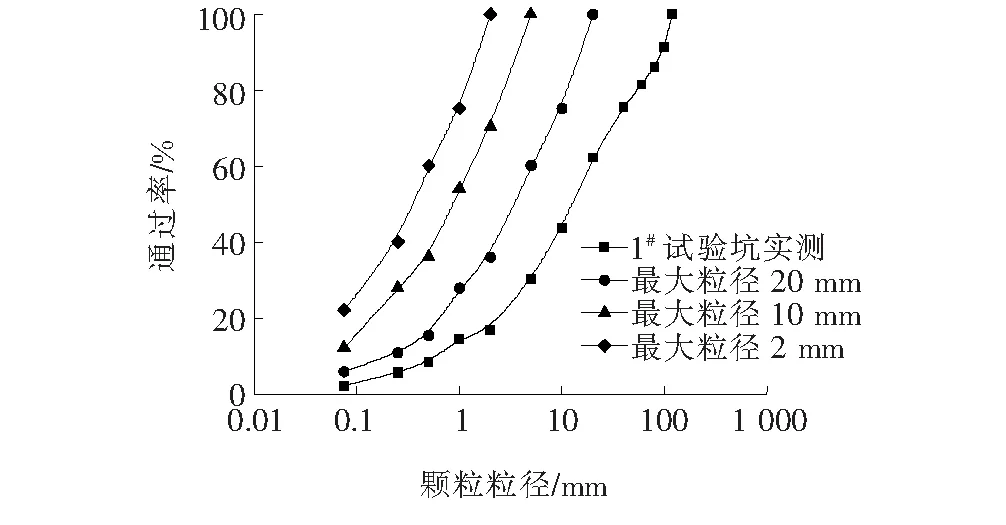
图2 现场填料及缩尺填料的颗粒级配曲线
然后按现场密实度(干密度1.79 g/cm3)将不同最大粒径填料人工击实成直径101 mm、高200 mm的标准中三轴试样。记录击实过程中不同试样所用能量如表1所示。表1说明试样粒径越大击实到同一干密度所需能量越大。
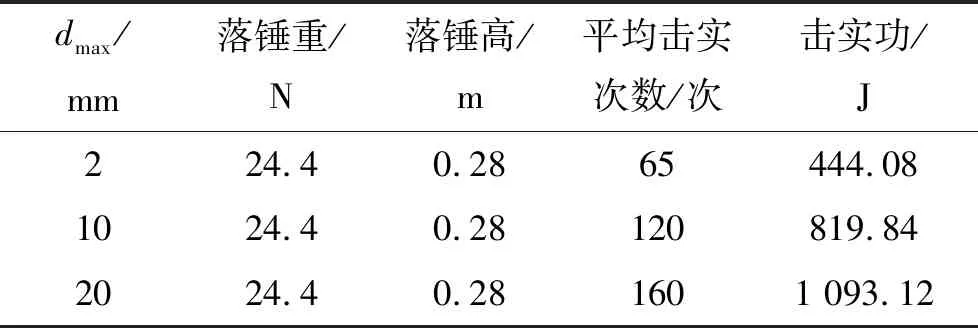
表1 压实填料制样过程中的击实功
2.2 三轴试验结果
将制备好的中三轴试样饱水后,在4种围压(100、200、300、400 kPa)下进行固结排水剪切(CD)试验,试验剪切速率取0.024 mm/min,加载到轴向变形为15%时停止试验。得到不同最大粒径试样的应力应变关系如图3所示。
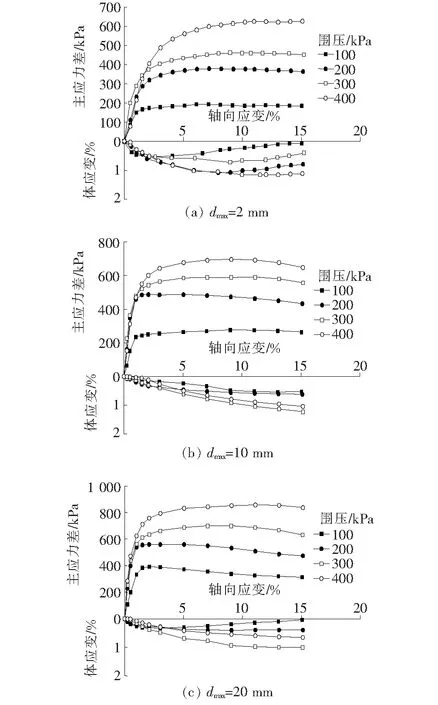
图3 三轴试验的应力应变关系曲线
由图3可知:不同最大粒径软岩填料试样应力应变曲线总的形态特征基本相似:ε1-εv曲线均显示低围压下试样先剪缩后剪胀,高围压下一直剪缩;(σ1-σ3)-ε1曲线在高围压下接近双曲线,而随着围压减小(σ1-σ3)曲线形态与双曲线差异越来越大。
取偏应力峰值点或15%轴向应变对应的偏应力为峰值强度,绘制摩尔应力圆并拟合强度包线,得到不同最大粒径的试样摩尔库仑强度指标见表2。表2表明:试样的黏聚力c和内摩擦角φ随着试样最大粒径的增大而增大。
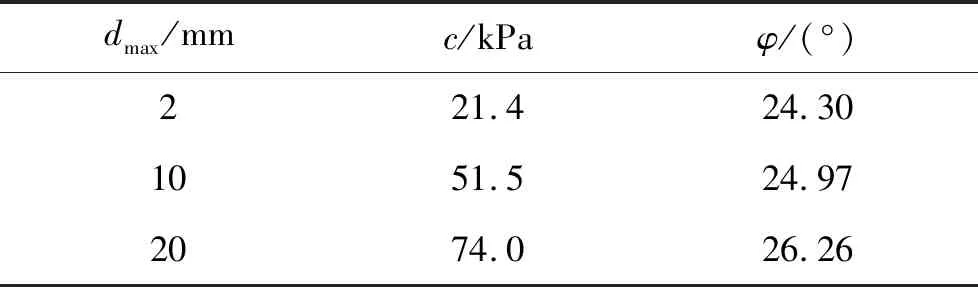
表2 不同最大粒径试样的强度参数
3 参数l的物理意义和确定方法
根据式(4)对试验结果进行非线性拟合反演得到参数l如表3所示。
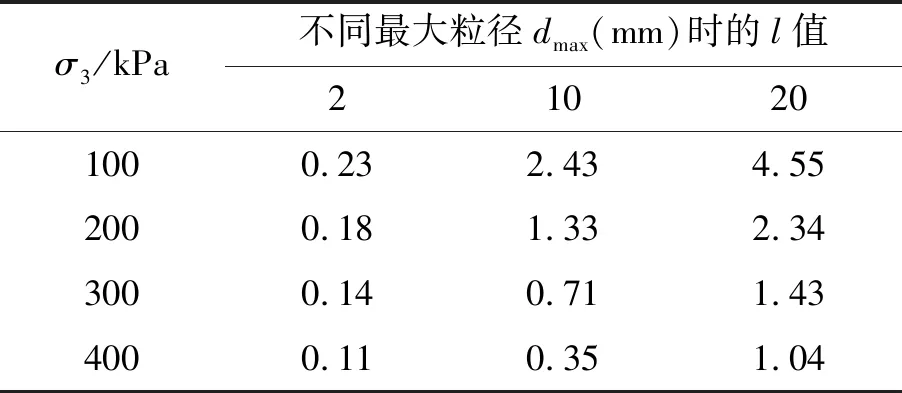
表3 参数l的反演计算结果
从表3可知:l值随着围压的增大而减小,随着粒径的增大而增大。试样在低围压下表现出剪胀特征,说明压实填土在低围压下表现出一定的结构性土的特征,从围压角度看,l值在一定程度上反映了试样的超固结性质;另一方面,结合表1击实过程中试样所需击实能量可知,击实土样因为受到强力机械作用,随着粒径越大试样在形成过程中吸收的能量越大,试样可以获得更紧密的结构,在低围压试验时,可呈现弱超固结的性质。可见l是一个反映压实填料压实过程的参数,该文称之为压实条件参数,该参数为无量纲参数。
据此,可假定l符合式(14)形式:
(14)
式中:p0为先期固结压力;σ3为围压大小;χ、ω为材料常数,与压实后的材料性质相关。
要依据式(14)确定压实条件参数l,首先要知道试样的先期固结压力。为此,该文开展了不同最大粒径试样的等压固结试验。为使文章简洁,不再赘述试验过程和数据处理过程,仅将最终得到的先期固结压力p0以及压缩指数Cc的结果列于表4。
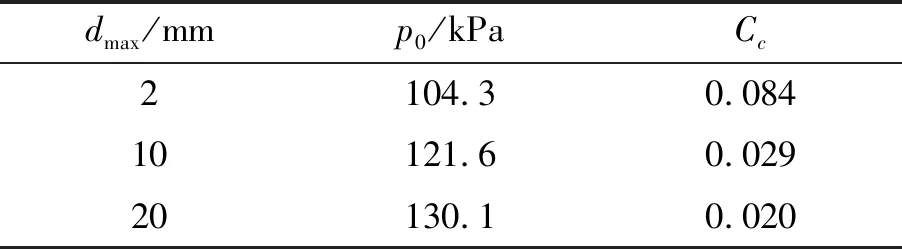
表4 各向等压固结试验结果
根据表3、4结果,分别拟合式(14)中的材料参数,结果如表5所示。
基于表5所得参数,将式(14)计算结果与试验结果绘制于图4中。结果表明:用式(14)确定参数l是合理的。
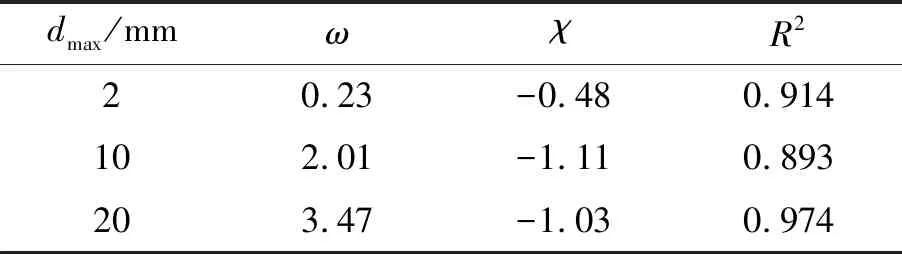
表5 各参数的反演结果
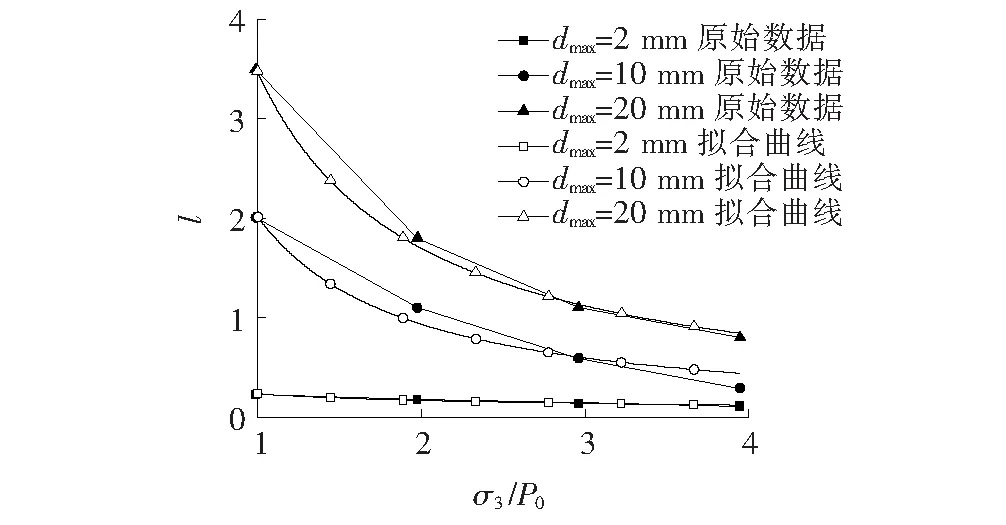
图4 公式(14)对l的拟合效果
4 改进邓肯-张模型效果
将式(14)代入式(13)中,得到完整的改进邓肯-张模型切线模量计算公式如式(15)所示:
(15)
其中:
改进邓肯-张模型参数共9个,分别为K、n、φ、c、Rf、Kb、m、χ、ω,比原邓肯-张模型参数多2个。其中7个参数的意义与邓肯-张模型相同。
为说明改进模型的效果,该文分别采用邓肯-张E-B模型和改进邓肯-张模型对前述软岩填料缩尺试验数据进行整理,得到模型参数如表6、7所示。由于不同最大粒径试样分析结果相似,限于篇幅,该文仅将dmax=20 mm的结果列出。
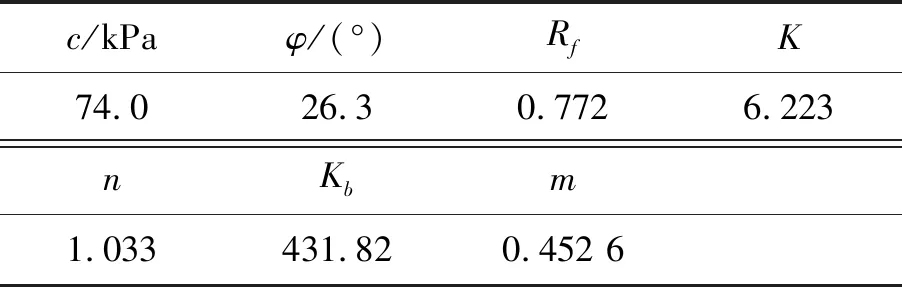
表6 E-B模型参数(dmax=20 mm)
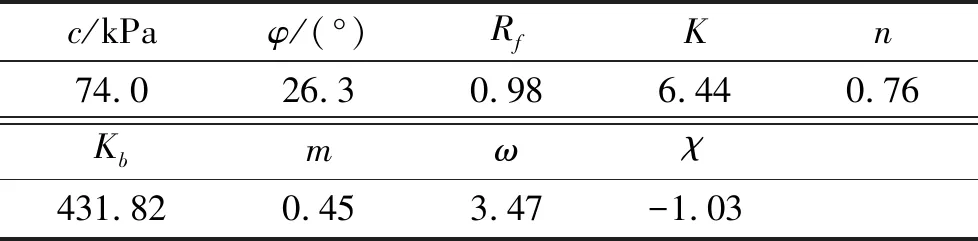
表7 改进邓肯-张模型参数(dmax=20 mm)
然后,将两个模型的预测结果与试验数据绘制在图中比较两个模型的效果,如图5所示。
图5表明:相比于邓肯-张模型,新模型显著地提高了各围压(尤其是低围压)下填料的应力应变曲线预测效果,是对邓肯-张模型的改进。改进后模型是对邓肯-张模型的微调,保留了邓肯-张模型意义明确、参数易于确定优势的同时,更适用于压实填料。
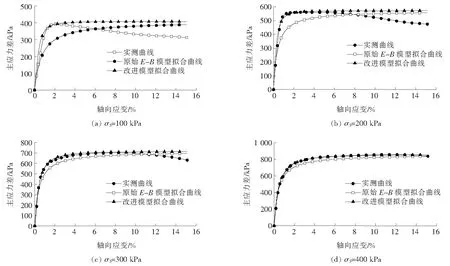
图5 E-B模型和改进模型预测效果(dmax=20 mm)
5 结语
针对邓肯-张模型不能反映压实土的(σ1-σ3)-ε1关系曲线在低围压下不符合双曲线的情况,在邓肯-张模型中加入一个压实条件参数l,得到新的(σ1-σ3)-ε1关系方程,基于此重新推导切线模量Et的计算公式,结合不同最大粒径软岩填料制样过程和三轴试验结果,提出了新参数确定方法,得到了改进的邓肯-张模型,最后将改进模型应用到压实软岩填料的三轴试验数据分析中,证明改进模型合理可行。该文提出的改进模型仅对邓肯-张模型进行了微调,保留了邓肯-张模型意义明确、参数易于确定、在数值软件中易于修改的优势,更适用于压实填料。

