数值核反应堆大数据及其应用

汪岸，任帅，苗雪，董玲玉，朱迎，陈丹丹，胡长军

北京科技大学，北京 100083

1 引言

数值核反应堆（以下简称数值堆）是一种基于超级计算机实现的软件系统，用于核反应堆内多物理耦合过程的高保真数值模拟和预测[1]。数值堆被当成实际反应堆“外在”和“内在”的镜像，可以支撑包括反应堆的设计、建筑安装、运行、退役等过程在内的全周期从微观机理到宏观现象的研究。数值堆在运行中涉及的大量数据通常有两种用途：一是用于建模优化，即作为耦合计算的中间数据，辅助模型的建立和改进；二是用于科学发现，即作为研究分析的原始数据，获取对材料、机理的认识。

这些数据在数值堆这一复杂的多物理场模拟系统中流动，且进行精细计算，可以轻易产生PB级的数据量，因此在存储上要借助高吞吐、高并发的并行文件系统，在计算上要依赖高性能、高可用的处理器资源。在不同计算尺度、不同服役环境下，数据虽然体现为不同的含义、形式，但是它们都属于与核反应堆相关的计算数据，相互之间存在紧密的关联。从计算的部分来看，数值堆是核反应堆各种物理过程及其耦合模拟的算法实现，其中各过程通过计算数据相连；从数据的部分来看，数值堆是核反应堆各种计算数据的关联和相互转换，其中各数据通过物理过程相连。

数值核反应堆大数据就是数值堆运行过程中涉及的数据总和。作为数值堆的关键组成部分，数值核反应堆大数据具有两方面不可忽视的重要作用：对“内”，它为工程人员提供了形式复杂、关联紧密的计算数据，对其关联性的研究可用于改进数值堆的模拟性能；对“外”，它为科研人员提供了大量可供进一步挖掘分析的模拟数据，其中可能蕴含着有关核反应堆材料、物理化学机理的新认识。大数据技术的引入使数值核反应堆大数据的价值比以往更清晰地呈现出来，从而为发挥数值核反应堆大数据对“内”和对“外”的作用奠定了基础。

本文提出了数值核反应堆大数据的概念，阐述了数值堆大数据最重要的特点。从这些特点出发，引出了不同于传统数值堆模拟的研究方向，也就是基于数据的建模优化和科学发现。以中国数值反应堆原型系统（China virtual reactor 1.0，CVR1.0）[2]为研究对象，本文论述了基于数值堆大数据的研究方向及成果，有力地证明了数据自身价值、数据与数据的关联性对数值堆研究的推动作用。

2 相关工作

随着计算机硬件水平的发展及核反应堆数据的积累，已有研究中利用机器学习、人工智能等技术手段对数值核反应堆大数据进行的挖掘分析着重于两个方面的研究工作：一是优化模拟模型，二是基于数据的挖掘分析进行科学发现。

2.1 数据驱动的建模优化方法

数据驱动的建模优化就是利用数值堆大数据改进数值堆的各种数值算法，具体涉及对整个计算模型或模型中部分模块的改进、替换，以及利用数据进行工况预测或模型计算。

（1）整个计算模型的改进和替换研究

改进、替换整个数值计算方法的研究重点集中在建立计算过程中输入与输出的非线性关系。例如，在中子学的研究中，基于细胞神经网络求解简单平板几何上的中子输运方程[3]；将基于人工神经网络的偏微分求解方法应用于非线性源扩散[4]、中子点动力学[5]、辐射输运[6]、一般非线性偏微分方程求解[7-8]等许多与数值堆相关的问题中。在计算流体力学（computational fluid dynamics，CFD）的研究中，利用基于小样本集的机器学习方法解决数据价值密度低的问题及求解流体力学的Navier-Stokes方程[9]。上述研究工作极大地节省了求解复杂方程所需的计算资源，但在比较复杂、缺少样本的几何条件下仍然难以达到理想效果。

（2）模型部分模块的改进研究

在模型的部分模块、算法中也可以基于数据驱动提出改进策略。例如，在计算流体力学的研究中，以核反应堆大数据为驱动修正现有湍流模型的经验系数[10]；利用深度神经网络从高精度模拟数据中学习雷诺应力各向异性张量模型[11]；利用监督学习算法建立湍流模型中的闭包项，并将闭包项插入计算流体力学数值模拟中，以得到更好的湍流物理表示[12]；通过训练卷积网格来预测任意给定几何的最优网格密度，加速最优网格的生成[13]。在材料势函数的研究中，通过机器学习对势函数库进行学习，开发用于势函数计算的机器学习模型，该模型可以在保证势函数精度的基础上将计算时间减少几个数量级[14-15]；将势函数机器学习模型和分子动力学（molecular dynamics，MD）模拟软件LAMMPS集成起来，扩大原有计算规模[16]。上述研究工作通过对部分模块或算法进行改进来达到优化模型整体的目的。

（3）工况预测或模型数据研究

还有许多研究集中在利用实验数据、设备数据直接进行工况预测，或者为数值堆提供计算数据。例如，在中子物理计算方面，基于人工神经网络的方法可用于中子深度剖面分析[17]及中子能谱解谱[18]。在计算流体力学方面，自联想神经网络可用于核电站在线监测及传感器校验技术构建[19]；支持向量机模型与多元状态估计方法可用于核电站的运行工况估计[20]；改进径向基函数网络模型和遗传算法可用于核电站瞬态工况诊断识别技术的构建[21]；利用机器学习等进行棒束子通道热工水力特性的预测[22]。上述研究不依赖对实际物理过程的理解，且训练数据充足，能被广泛应用。

2.2 基于数据挖掘分析的科学发现

基于数据的挖掘分析进行科学发现是数值核反应堆大数据研究的重要目标之一。近几年，机器学习算法已被有效地用于材料和分子的原子尺度模 拟[23-24]，应用领域包括探索结构与属性之间的关系以及模式匹配，以指导材料设计和预测新化合 物[25-26]。随着计算能力不断增长，模拟生成的数据越来越多，使用机器学习从数据中提取知识变得越来越重要[27]。无监督机器学习算法可用于数据模式的探索、可视化和分类，而无须训练样本（具有相应输出值或类别标签的样本输入），它已被有效地应用于材料和分子科学领域[28-29]。然而，无监督学习在辐照损伤研究领域的应用仍然处于起步阶段。由国际原子能机构（International Atomic Energy Agency，IAEA）开发的建立级联碰撞MD模拟的开源标准化数据库CascadesDB[30]为这个方向上的未来工作奠定了基础。例如，基于该数据库，利用聚类的方法开展对MD级联碰撞数据的分析研究[31-32]。针对点缺陷分析，传统的方法无法区分基于点缺陷的聚类[33]。例如，传统的方法使用位错提取算法（dislocation extraction algorithm，DXA）来确定位错环[30]，但是无法识别非位错缺陷和小团簇的形态。此外，随着系统规模的增大，位错提取算法会占用大量内存，并且速度很慢。传统的几何方法（如邻域分析等）能够识别晶体中的缺陷区域，但无法描述缺陷的形态和浓度。通过设计新的几何特征向量，可以识别晶格原子中的缺陷，并将其可视化[34-35]。

3 数值核反应堆大数据特点分析

数值堆涉及的数据主要有两种不同来源，一是在实验、运维等过程中由核反应堆及相关设备产生，二是在数值堆运行过程中由各种算法产生。这些来源使数值堆大数据具备了工业大数据和模拟大数据的特征。由于数值堆的领域特点，模拟大数据最重要的特征是多样性、关联性，以及由数学物理模型和数值方法带来的非精确性。

多样性和关联性是模拟大数据的重要宏观特征。多样性体现在数据类型丰富、数据版本多样。例如，反应堆材料从设计到投入使用要经历成分设计、微观组织调控、工业测试、服役等多道工序，其服役周期达几十年之久，材料性能在不同的时效作用下也会呈现不同的特点。此外，来源于设备和计算的数据是多样的，如原子坐标数据、团簇数据等。关联性体现在数据含义、形式的紧密关联上。例如，反应堆材料的使用寿命与各服役阶段息息相关，优异的服役性能离不开精确的系统测试，离不开大量的工艺参数调控，更离不开合适的成分、结构设计，而每一工程阶段的相应计算工作会涉及不同物理过程、不同时空尺度的数据，各个阶段之间不同来源的数据具有极其复杂的关联关系。

非精确性是模拟大数据的重要微观特征。数值堆包含大量数学物理模型，这些模型是对现实的近似描述，使得数值堆从设计、实现到交付经历了多个层次的近似处理[36]。最终，数值堆大数据中占主要部分的数值型数据包含了不同来源的误差。这些误差的存在促使研究人员追求高精细的模拟以贴近现实，这是数值堆大数据在数量上快速增长的根本原因之一。从近似处理的层次来看，非精确性体现在数学物理模型、数值方法和计算机程序带来的误差上。依据现实建立数学物理模型，是对真实现象在某一组条件下的理想化处理，这一阶段会因条件简化引入一定的误差，如运输过程的粒子模型、冷却剂的流体模型。依据数学物理模型建立数值方法是在有限的计算资源下寻求复杂方程的数值解，并且量化地描述收敛性、复杂度等具有普遍性的特点。这一阶段因离散化引入一定的误差，例如热工水力流体计算和堆芯结构力学计算涉及的有限元方法会受到时间、空间离散误差的影响，MD和动力学蒙特卡洛（kinetic Monte Carlo，KMC）等依赖随机数和随机过程的方法会受到统计误差的影响。依据数值方法开发计算机程序，引入的误差都可以归结为舍入误差。尽管浮点数的模型（单精度、双精度等）以及它们的运算特点在数值方法层面已经得到完整的讨论，并且数值方法已经给出了准确的算法，计算机程序从编码、编译到最终运行的一系列活动仍然无法保证完全贴合它要表达的数值方法。例如，在不同机器上计算同一数学基本函数可能得到不同结果；某些语言的编译器为了保证效率会对原程序代码做一些变换；数值堆计算程序的并行化版本可能会极大地改变原本的浮点运算相关公式和计算顺序。

多样性、关联性和非精确性相互影响，使得面向数值堆大数据的研究能够基于神经网络、数理统计、数值分析等多个细分领域进行。

4 基于数值核反应堆大数据的建模优化

4.1 基于第一性原理数据和神经网络模型的分子动力学势函数建模

势函数计算是材料多尺度模拟关键的一环，也是数值堆高精细模拟实现过程中计算复杂且耗时的部分。MD和KMC中粒子速度、位置的更新，以及随机团簇动力学（stochastic cluster dynamics，SCD）中多元组分材料参数的计算均离不开势函数模型。过去常用的势函数模型通常包括两种，一种基于第一性原理，另一种基于经验函数。前者往往计算复杂，且对于多元合金组分而言，第一性原理势函数的构建过程非常复杂；后者虽然在效率上有所提高，但精度往往不够，对于多元合金组分而言，经验势函数的构建过程更加困难。基于密度泛函理论（density-functional theory，DFT）计算得到的海量数据，提出一种基于机器学习的方法对原子体系模拟参数及势能之间进行拟合的势函数模型——基于人工智能的势函数模型（artificial intelligence based potential model，AIPM）。

AIPM训练所需的时间与原子数量相关，在原子数量相当大时，需要通过采样获取适当规模的训练集。由于数值大数据具有非精确性的特点，不同的数据采样方法可能会导致模型计算结果产生波动。本节不考虑上述采样问题，而是基于筛选好的原子数据验证AIPM。

选取2 000条由DFT计算得到的数值计算大数据，每条数据代表一个原子体系，训练集由1 000个原子坐标及对应的体系势能组成。随后，使用FeCu二元合金体系基于原子坐标进行机器学习模型的特征提取。具体来说，首先按照最近邻法对原子邻域进行划分，并以该原子为中心建立局域坐标系，如图1所示，将第一近邻和第二近邻分别设置为x轴、y轴坐标，将二者的向量积作为z轴坐标，于是可以得到每个原子的坐标，将这些坐标作为神经网络的输入。如图2所示，使用3层全连接的神经网络结构，每层的节点数依次为15、10、6，拟合得到体系内一个原子的势能，然后针对其他原子采用相同的方案进行拟合，最后将所有原子的势能求和，即可得到总的原子体系的势能，将这一势能与数据库中给定的势能进行比较，验证模型的精度。采用AIPM计算1 000个粒子大小的FeCu原子体系势能，并与嵌入原子法（embedded atom method，EAM）势函数模型进行对比，结果见 表1，对比结果验证了AIPM的可靠性。模拟结果显示，与EAM相比，AIPM在计算耗时上缩短一半以上，同时计算结果仅有0.7%的相对偏差。将该模型应用于数值核反应堆的高精细模拟，有望实现模型的加速和更大规模的模拟。

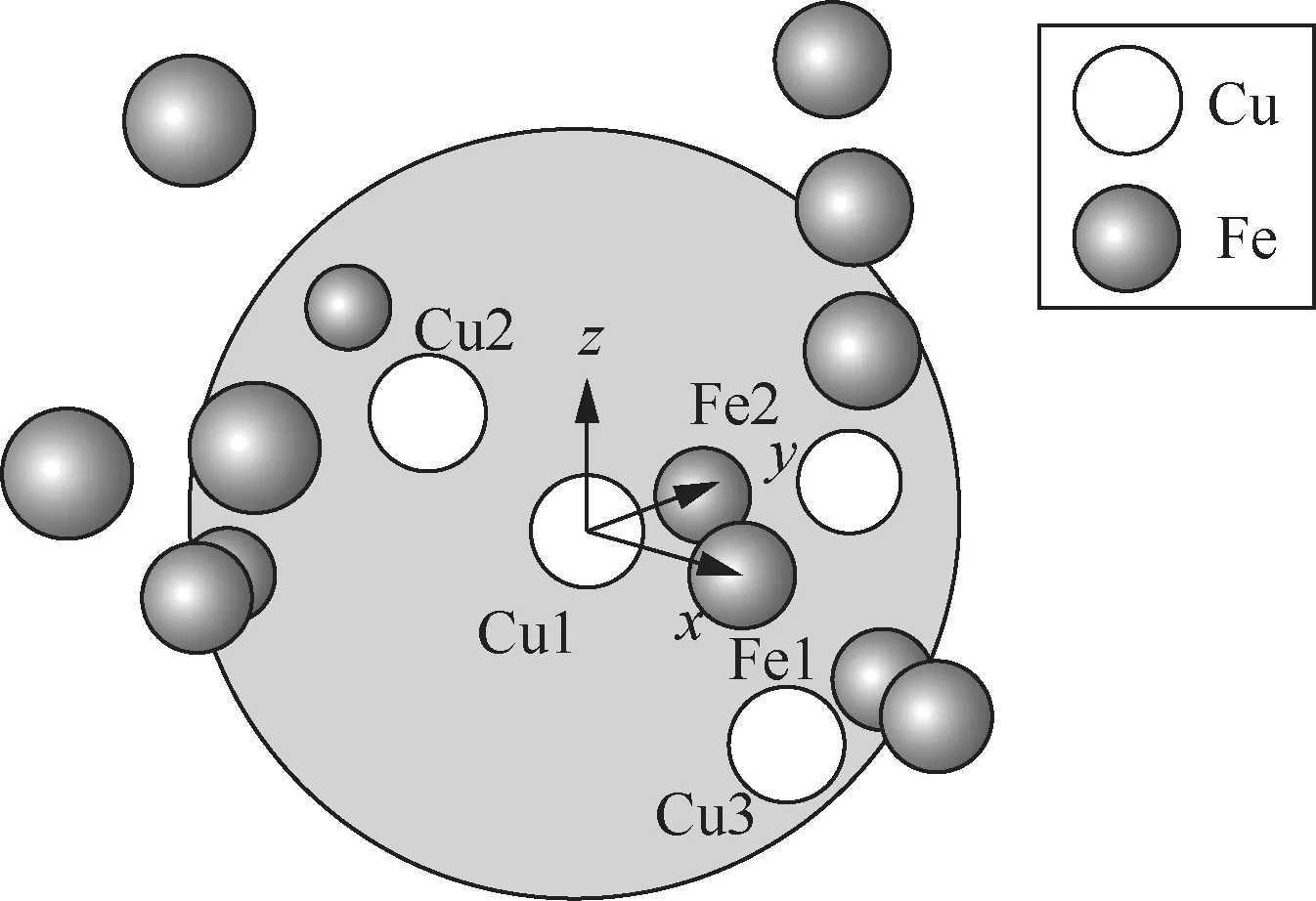
图1 局域坐标系的建立方法

表1 FeCu原子体系神经网络计算结果

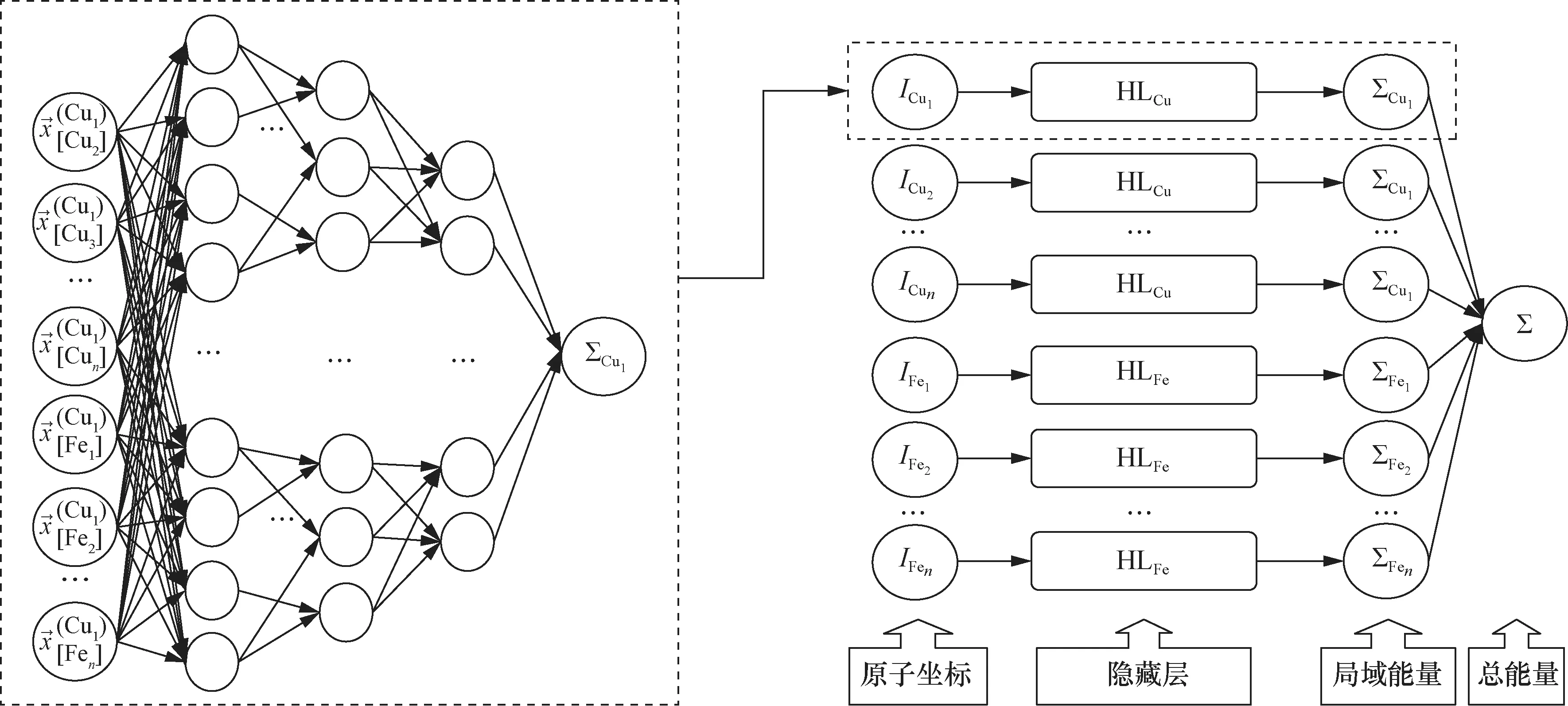
图2 FeCu原子体系神经网络构建过程

4.2 基于特征线法数据的敏感性分析

中子输运是数值堆的核心过程之一，它以核数据、堆芯空间信息等复杂时空数据为输入，产生有效增殖因子、中子通量密度分布等描述堆芯核裂变反应状态的数据。特征线法是一种经典的中子输运数值迭代方法，它将连续的空间离散为有限条相互交错的轨迹，将空间上的输运方程求解问题转化为沿轨迹的常微分方程求解问题。如 图3所示，特征线法产生的结果会随输入数据的变化而变化，这一敏感性问题是由数值方法本身带来的，并且在计算程序日益复杂化的情况下难以从解析表达式入手解决。使用基于大量数据的统计方法可以让算法从输入和输出中挖掘数据之间的关联性，建立输入变化与输出变化之间定性甚至定量的关系，从而加深对特征线法计算结果波动的理解，也可使得输入数据的选取更加合理、高效。同时，使用尽可能少的数据来建立统计模型，并将它用于更大输入空间中输出数据的波动预测，从而避免尝试各种输入数据组合带来的计算资源的浪费。

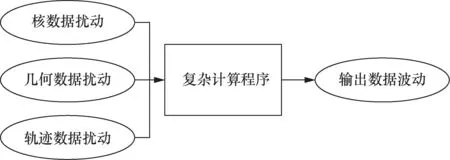
图3 输入数据变化引起输出数据变化

以三维特征线法程序ANT-MOC为例[37]，它执行特征线法计算所需的堆芯空间信息包括轨迹分布，该分布可以由一些参数完全确定，其中最重要的参数是方位角（轨迹的平面角度）数量、平面轨迹间距（轨迹在平面上投影的间距）、极角（轨迹的轴向角度）数量、轴向轨迹间距（轨迹在轴向上的间距）。调整角度数量和间距大小就能改变整个空间中轨迹的密度，也就改变了离散化的方程数量。

本文基于ANT-MOC考察方位角数量、平面轨迹间距、极角数量和轴向轨迹间距这4个影响轨迹分布的关键参数对计算结果中有效增殖因子keff的影响。有效增殖因子是用整个堆芯中的中子通量密度计算得到的堆芯裂变反应的整体度量，因此它在输出数据中具有一定的代表性。实验选取的计算对象为Takeda国际基准题[38]，它描述了一个简单的压水堆堆芯，其有效增殖因子的参考值kref为0.977 8。实验所用的输入数据中仅有4个变量，它们的取值 见表2，取值组合共500种。

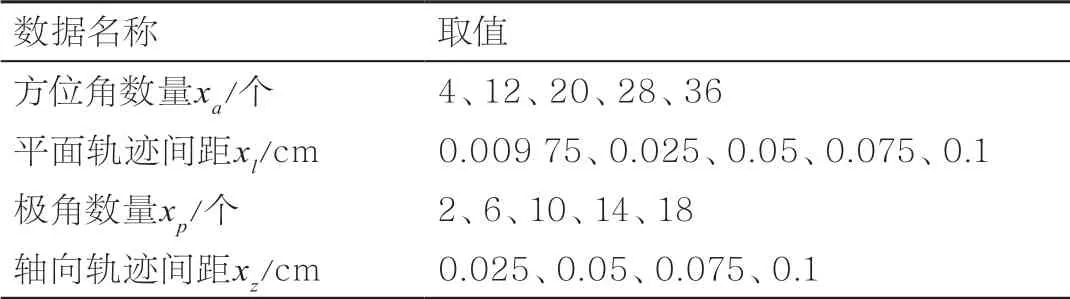
表2 轨迹分布相关输入数据的取值

使用ANT-MOC完成500组计算后，计算每个有效增殖因子keff与参考值kref的相对误差。由于输入参数的取值范围不大，在这一范围内使用线性模型近似地研究各参数与相对误差的关系。给定显著性水平0.05，可以为这500组数据建立四元线性回归模型：

可以使用该模型估计keff的相对误差随轨迹分布的变化情况。回归分析的各参数见 表3。

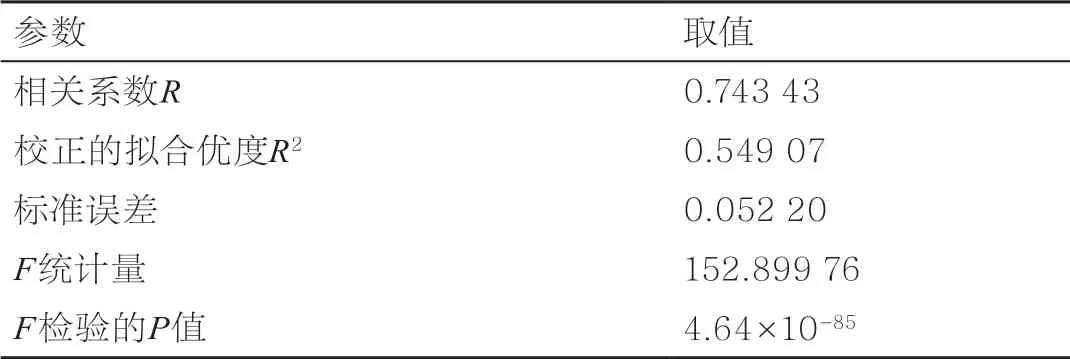
表3 500组样本的多元回归分析参数

相关系数R和校正的拟合优度R2的数值表明有效增殖因子keff的相对误差与选取的4个变量有较好的相关性，F检验的P值远小于0.05表明结果非常显著。各变量的t检验结果见表4，结果表明，方位角和极角数量与结果的相关性非常显著（P值远小于0.05），参数标准误差也表明这两个参数的平均偏离程度较小，这说明四元线性回归模型比较合理地估计了方位角和极角在一定范围内的变化对ANT-MOC计算结果的影响。在Takeda计算中，根据拟合结果以及表2描述的参数区间，还可以比较在参数区间内相对误差随不同参数变化的波动情况，从而指导具体计算时的参数选择。例如，方位角和极角的线性拟合系数为负、平面轨迹间距的系数为正，意味着在一定范围内使这3个参数精细化可以缩小相对误差；轴向轨迹间距的系数为负，意味着ANT-MOC的计算结果难以通过该参数的精细化（缩小）来改善。

表4 各变量的t检验结果

线性拟合在一定范围内定量地反映了ANT-MOC计算结果对参数的敏感性，从而可以避免复杂的误差放大和条件数的理论分析，快速给出筛选参数组合的统计依据。对于相当精细的参数空间，ANTMOC数值算法的收敛速率不可以忽略，计算结果的相对误差不再能被线性模型很好地描述，需要在此工作的经验上使用更复杂的学习算法来建立估计模型。

4.3 流固耦合中基于三维R树的大规模流体数据插值分析

热工水力软件CVR-PACA和结构力学软件CVR-HARSA（原CVR-HISRES）的流固耦合模拟是CVR1.0项目的研究重点。PACA与HARSA耦合旨在进行全堆规模的流致振动分析、获得燃料棒和固定支架间的磨损评估数据，有助于堆芯安全分析、设计及反应堆延寿。耦合的本质是完成流固交界面上数值数据的融合转换，其中，数值数据具有数据量巨大、不匹配的特点。数据量巨大是由PACA与HARSA高精细模拟计算的特点决定的，而不匹配是两者建模的网格类型和密度不同导致的。基于此，利用三维R树[39]索引大规模流体数据，完成了PACA输出的流体压力向HARSA的插值计算，即流体压力数据的融合转换计算。实验表明，此种插值计算方式提高了流体压力的融合转换效率和大规模高精细耦合计算效率。

PACA输出的流体数据规模巨大，如10 mm长的双流道模型的顶点数目超过30万；100 mm长的6流道模型的顶点数目超过900万，因此采用三维R树索引大规模流体网格顶点进行流体压力数据的插值计算。另外，PACA输出的网格顶点难以还原拓扑结构，因此在数据融合转换过程中采用邻近点加权平均[40]的匹配计算方式。流体压力数据的整体插值过程包括图4所示的3个阶段。

图4 流体压力数据插值过程展示

● 数据清洗阶段：获取PACA计算输出的原始数据，原始数据中存在许多重复数据和融合转换计算不需要的数据，该阶段对这部分数据进行清洗处理，并输出后续计算所需数据，即流体网格顶点及各顶点对应的压力值。

● 构建三维R树阶段：对上阶段输出数据进行三维R树的构建，其中，树中叶子节点包围的是三维空间中的流体网格顶点，每个顶点都唯一对应一个压力值属性。

● 匹配计算阶段：针对每个固体网格顶点遍历三维R树，搜索距离它最近的前k个流体顶点，并对这k个顶点及压力值进行邻近点加权平均计算，得到固体顶点对应的压力值。

经过上述计算，得到每个固体网格顶点对应的压力值，然后将这些顶点及对应压力值输出为HARSA计算所需的格式。

利用表5中的6组建模数据进行实验，测试了直接插值方式和基于三维R树的插值方式在不同条件下的性能，分别用BaseLine、RTree表示这两种插值方式。其中，直接插值方式直接搜索所有流体顶点，找到距离每个固体顶点最近的k个流体顶点，并进行加权计算得到该顶点对应的压力值。

表5 实验测试数据

图5（a）展示了燃料棒数目变化时，PACA与HARSA耦合时两种插值方式的耗时，其中纵轴为消耗时间的对数表示。当燃料棒数目增大时，RTree的耗时远小于BaseLine的耗时。图5（b）展示了燃料棒长度变化时两种插值方式的耗时。当燃料棒长度增大时，RTree的耗时仍远小于BaseLine的耗时。可见，RTree在高精细插值模拟中更具优势。

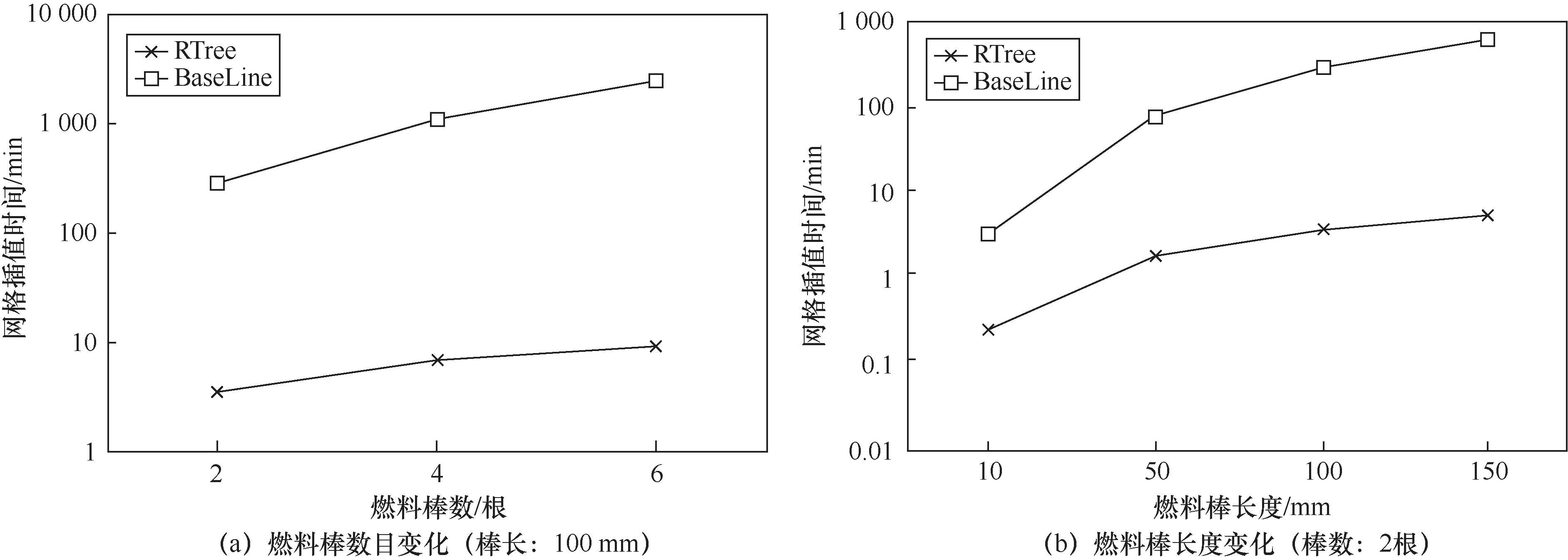
图5 流体压力数据插值计算效率测试

5 基于数值核反应堆大数据的科学发现

5.1 基于并查集算法的级联碰撞团簇划分方法

级联碰撞模拟后，高能粒子的撞击导致材料原子离开原本所在的晶格位置，而后进一步聚集或湮灭，形成自间隙团簇或空洞，最终导致材料力学性能降级，从而威胁反应堆设施的安全。基于CVR1.0中的分子动力学程序MISA-MD的模拟数据，采用并查集算法可以实现对团簇的有效划分。

数据集采用的晶体结构均为体心立方（body-centred cubic，BCC）晶体，元素都是铁（Fe）元素，晶格常数为2.855 32 nm。模拟数据均来源于大小为[80, 80, 80]的模拟区域，区域大小的含义是x、y、z方向上都是80倍的晶格常数，即80个晶格点。当实验环境的温度为600 K时，随着入射中子能量的不同，时间步长有10 000和100 000两种，总的时间步数有41 000和131 000两种，MISA-MD运行时，每隔1 000时间步输出一个结果，这里选取最后一个时间步的结果。每个时间步的结果数据都是.dump坐标数据，其中包含1 024 000个原子坐标。在上述实验环境下，数据涵盖不同初级离位原子（primary knock-on atom，PKA）能量、不同PKA入射方向，且每种能量每种角度都进行了多次模拟，包括10 keV、30 keV和50 keV共3种不同的能量，<122>、<135>和<235>共3个不同入射方向（以晶向表示），每种参数组合都进行了50次模拟，最终有450次模拟数据。

常规方法是将每个缺陷看成一个单缺陷的团簇，然后遍历其他缺陷，将指定距离内的缺陷加入该团簇进行缺陷的合并。该问题看起来并不复杂，但是当数据量大时，若采用常规方法来解决，往往时间复杂度过大，这是因为它需要反复查找一个缺陷所在的团簇，所以常规方法不能很好地解决该问题。这里采用并查集算法来解决。并查集算法[41]采用一种树形数据结构来处理这种不相交集合的问题。并查集算法有两种操作：合并（union），即把两个不相交的集合合并为一个集合；查询（find），即查询两个元素是否在同一个集合中。所有元素合并完之后，森林中有几棵树就有几种集合。因为并查集算法的数据结构为树形，所以树的高度越高，时间复杂度就越高。因此这里选取的是优化的并查集算法。使用优化的并查集算法划分团簇的伪代码如下。首先设置一个大小与缺陷总数相同的根节点数组root，它的含义为该缺陷所属团簇的编号，初始时将每个缺陷视为单独一个团簇，因此初始数组的值为自身编号。然后设置一个大小与缺陷总数相同的高度数组height，它表示以当前节点为根节点的树的高度，因为初始时每个缺陷都是一个团簇，也就是一棵树，所以初始时树的高度都为1。接下来计算任意两个缺陷之间的距离，在计算的过程中需要判断这两个缺陷的类型。如果这两个缺陷都是间隙原子或者一个是间隙原子、一个是空位，则只要它们的距离在一倍晶格常数（第二近邻）内，就认为它们属于同一个团簇；如果两个缺陷都是空位，且它们的距离不超过晶格常数的2的平方根倍（第三近邻），则认为它们属于一个团簇。如图6所示，此时缺陷2和缺陷9在距离阈值内，第一步先查找两个缺陷的根节点，在查找的过程中，将向上经过的所有缺陷的根节点都设为最上层的缺陷，也就是都直接接到根节点上，这被称为路径压缩，可以降低树的高度，使得以后向上查找根节点时速度更快。在获取根节点后，根据树的高度数组height判断两个根节点的树的高度，将高度小的树接到高度大的树上，如果树高一样，则可以将任意一棵树接到另一棵树上作为孩子节点。遍历根节点数组，将根节点相同的缺陷划分到一个团簇中，从而获得所有团簇的划分结果。将获得的所有团簇信息（包括团簇中的缺陷坐标、缺陷对数、缺陷类型（间隙或者空位）等）存储到团簇数据库中，最终获得了4 483个团簇。

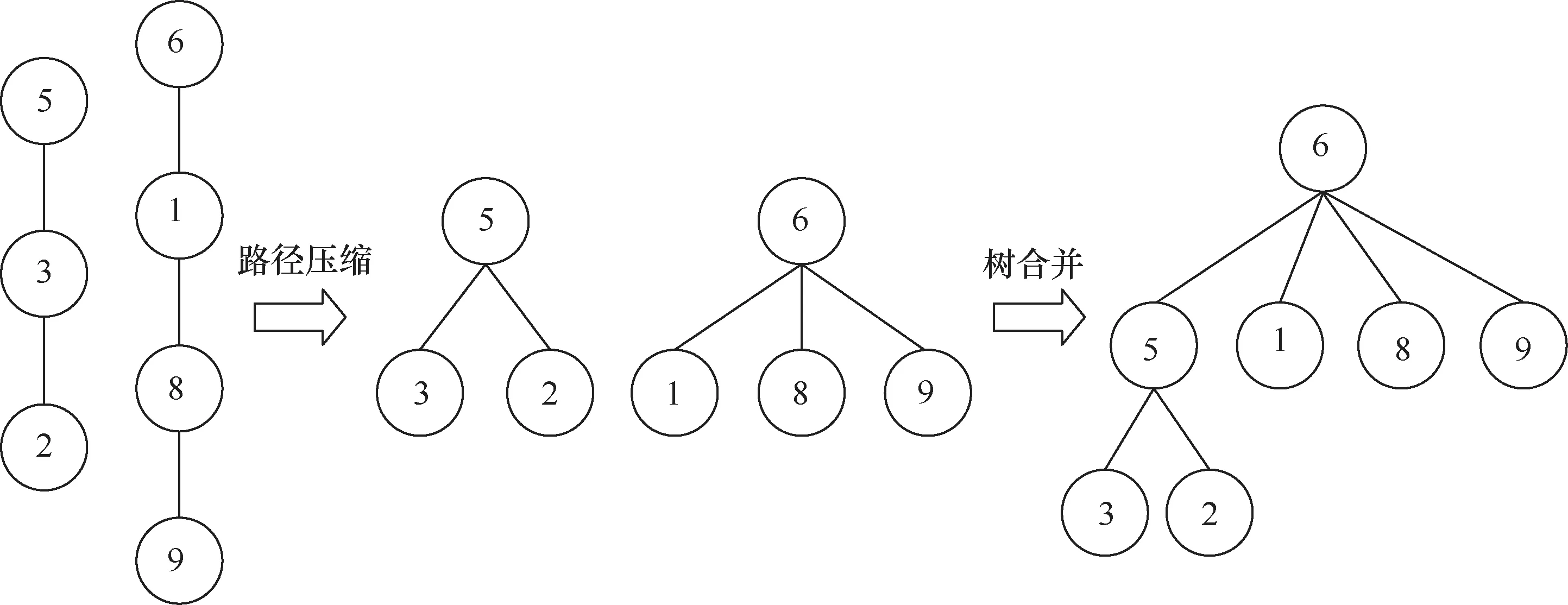
图6 并查集算例演示

伪代码1 使用优化的并查集算法划分团簇

输入：所有缺陷原子坐标 DEFECTS = [d1,d2, …,dm]

输出：所有团簇

1 设置树的根节点数组和高度数组： root = [1,…,m], height = [1]*m

2 fori← 1, 2, …,mdo

3 forj←i+1,…,mdo

4 if distance(di,dj) < threshold then

5a← 找到i的根节点

6b← 找到j的根节点

7 根据树的高度数组修改根节点数组

8 end if

9 end for

10 end for

11 将同一根节点的缺陷划分为一个团簇

12 输出所有团簇

5.2 基于KMC团簇大数据的环状团簇识别算法

KMC团簇大数据库包含了不同实验条件下经KMC长程演化后的原子团簇信息。KMC团簇大数据库包含PKA能量、PKA入射方向等实验参数以及团簇中各个原子坐标、空位、间隙原子数目等信息。这里共选取500条团簇数据展开分析。因为团簇形态和数目信息是未知的，所以有监督的学习方法在此不适用。无监督的机器学习方法在解决这一问题上具有独特优势，这里采用基于密度的聚类算法。首先，选取的特征向量为缺陷团簇中各缺陷与几何中心的距离、每两个缺陷与几何中心形成的夹角。考虑到几何形状经旋转、放大、缩小后仍然是相同的，对于角度，这里每隔5°形成一维数据，共有36维数据；对于距离，每次将所有的距离除以当前团簇的最大值，进行归一化处理，每隔0.025形成一维数据，共40维数据，因此特征向量为76维数据，如图7所示。选取HDBSCAN聚类算法对团簇进行识别，轮廓系数达到0.643。HDBSCAN聚类算法是一种基于密度的无监督的聚类算法，不需要标记过的数据，也不需要事先知道要划分的类别数。它可以对不同密度的团簇进行聚类，可以忽略噪声，且效率较高。团簇聚类结果 如图8所示。这里使用卡方距离作为相似性度量，使用轮廓系数（silhouette coefficient）作为聚类性能的内部评价指标，若轮廓系数接近1，则说明样本聚类合理；若轮廓系数接近－1，则说明样本更应该分类到另外的簇；若轮廓系数近似为0，则说明样本i在两个簇的边界上。图8中的所有缺陷团簇被分为几种不同的类别，每种颜色代表一种类别。本实验共获得了22种形状类别，从这22种类别中随机选取两种类别，每种类别选择两个团簇，将其进行可视化展 示。图9为类别1中的两个团簇，1 260和1 867是它们在数据库中的编号，它们具有完全相同的形状，都是四个角构成一个方形，然后有一个 顶点。图10则是另一个类别中的两个团簇，它们和类别1不同，它们的缺陷个数有6个，而且它们分为上下两排，每排3个缺陷，这两排构成近似平行的几何形状。

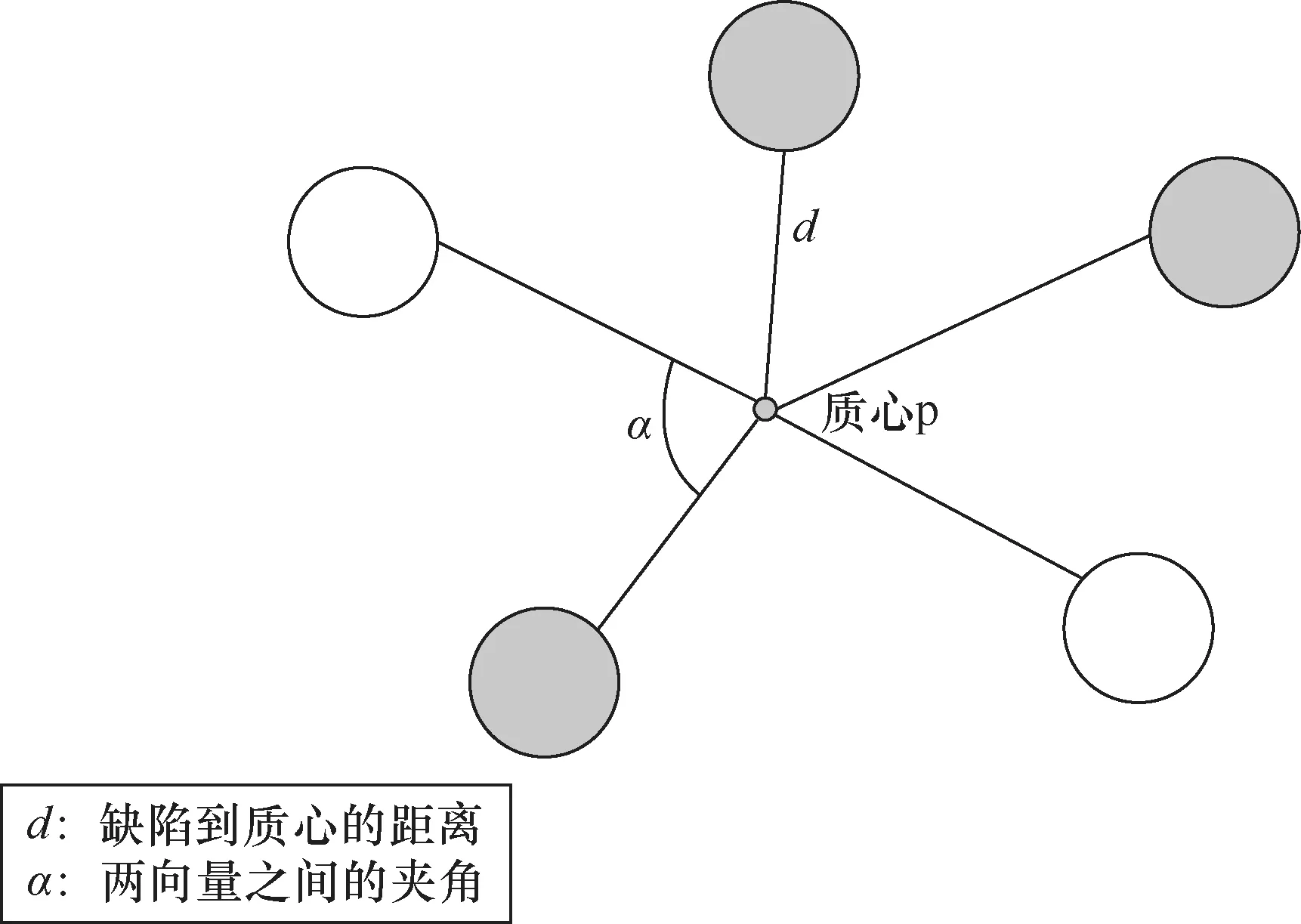
图7 团簇特征提取方法示意

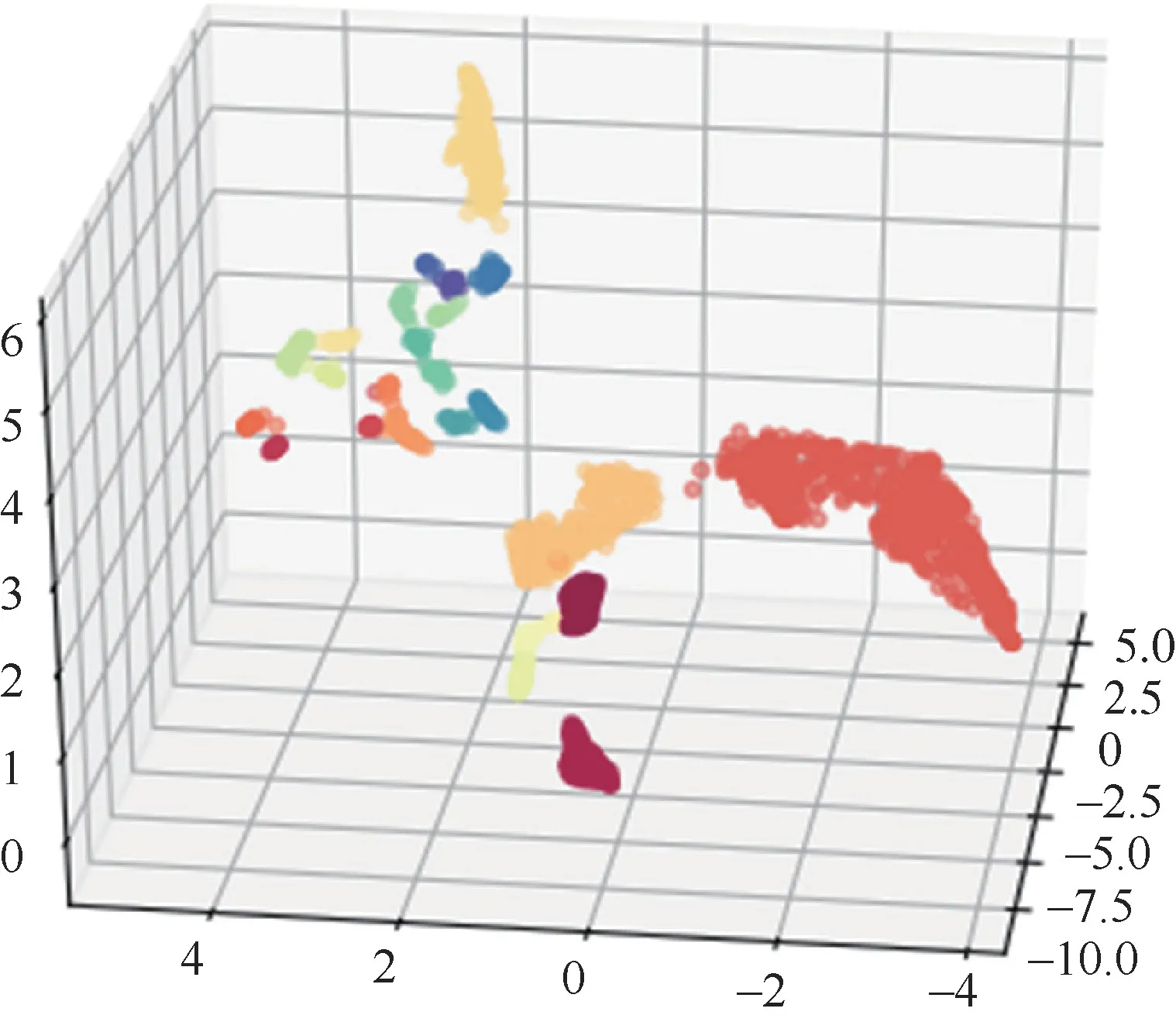
图8 团簇聚类结果

从图9和图10可以得出，本文采用的相似性度量和聚类算法是可行的，它们可以将形状相似的团簇聚类到一起，证明了整个程序的可行性。基于该方法，笔者在KMC长程演化数据中发现了一些类环状的团簇，如 图11所示，这一发现与之前报道的材料辐照实验中存在类环状缺陷团簇的结果相吻合[42-43]。针对团簇的研究仍处在初步阶段，不同形态的团簇对材料性能的影响机理尚不明确，基于KMC团簇大数据和机器学习的方法，实现了KMC长程演化后团簇形态的识别和分类，为后续团簇影响机理的研究提供了智能化手段。

图9 类别1的聚类结果

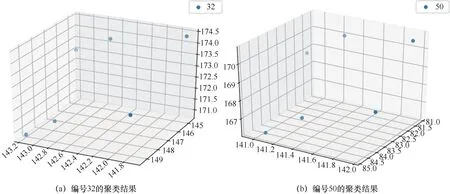
图10 类别2的聚类结果

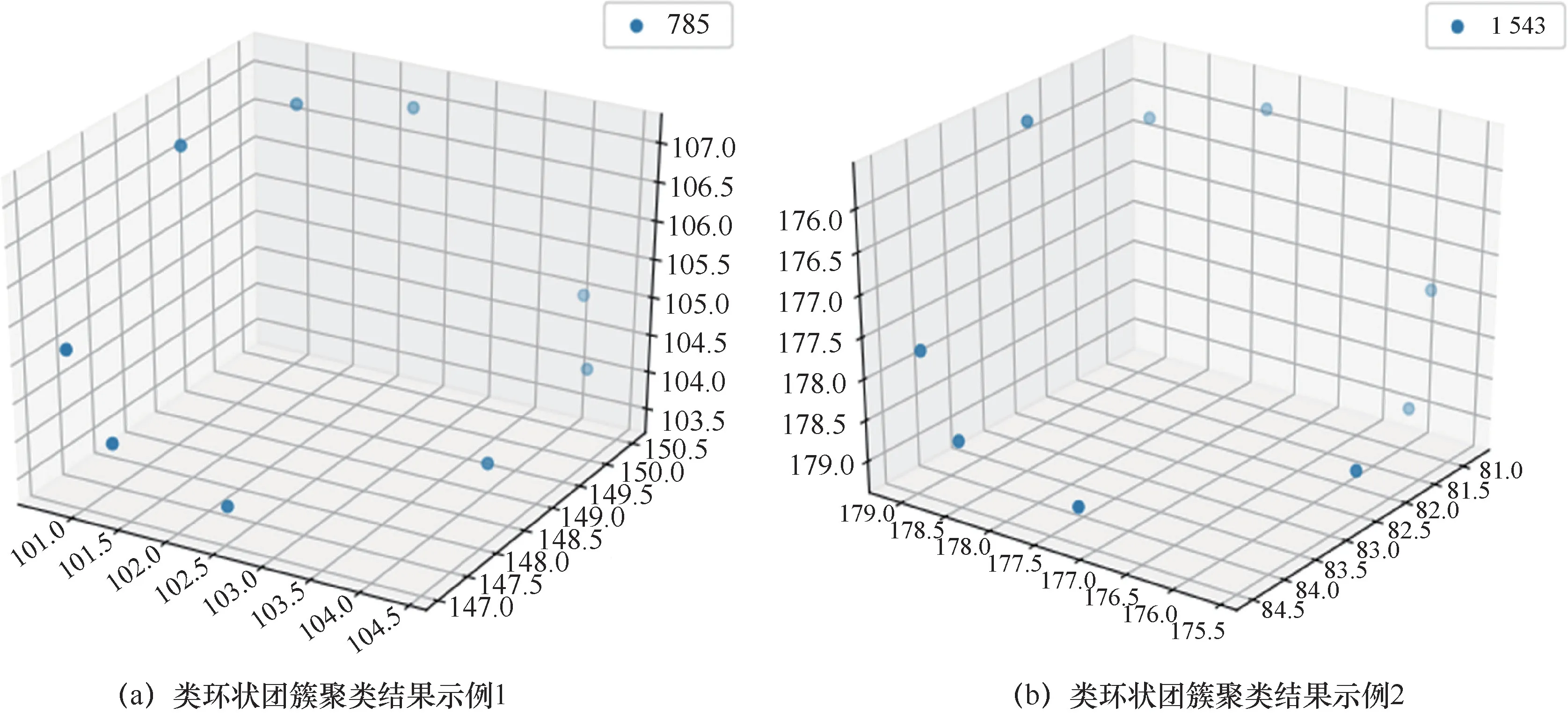
图11 KMC长程演化产生的类环状团簇聚类结果

6 结束语

本文提出了数值核反应堆大数据的概念，分析了它具有的多样性、关联性和非精确性等关键特征，并将这些特征和实际数值堆研究结合起来。将数值堆大数据看作数值堆的一个重要组成部分，使得大数据技术和学习算法的思想自然地被引入数值堆的研究中，拓展了研究的思路。从数值堆大数据的特征出发，本文指出了它最重要的两大应用方向：建模优化和科学发现。以CVR1.0为例，在基于数据的建模优化方面，基于神经网络的势函数改进了分子动力学总势能的计算，降低了整个模拟的计算时间；基于统计的敏感性分析和基于三维R树的网格插值研究了模拟数据之间的关联性。在基于数据的科学发现方面，基于聚类的团簇划分和环状原子簇发现，通过学习算法建立了有效的缺陷识别模型，有助于对材料性能进行预测。这些研究工作表明，数值核反应堆大数据概念的建立对于数值堆研究有极大的指导意义。

同时，上述研究也反映出用于数值核反应堆大数据研究的学习模型面临着易用性、准确度和效率等多方面的取舍，目前尚未形成一套具有领域特色的系统的研究方法。在今后的工作中，建立更可靠的学习模型和更完善的误差分析是数值核反应堆大数据应用的努力方向。