粉质黏土导热系数变化规律及模型预测

王叶娇，丁科竞，徐云山

(1.上海大学 土木工程系，上海 200444；2.桂林理工大学 广西建筑新能源与节能重点实验室，广西 桂林 541004)

城市地下电缆的载流量是电力系统负荷调度的重要指标，载流量过高会导致电缆事故，而载流量过低会造成电力电缆资源浪费[1].直埋式电缆的载流量不仅取决于电缆的长期工作温度，还与电缆周围土体的热水力特性有关.通常电力电缆埋置深度较浅，浅部土体的工程特性受周围环境因素如温度、含水量等的影响较大.然而目前在电缆载流量的计算过程中只对周围土体的导热性进行粗略的估算，并没有实时监测数据或者寻找适用于评估土体热特性的计算模型，因此对于准确核算电缆载流量工作带来了困难.

土体的导热系数是研究非饱和土水-热-力特性及其模型计算的重要参数，影响因素较多.Yunshan Xu等[2](2019)通过热探针法发现随干密度增加，温度对导热系数影响减小；张婷，杨平[3](2012)通过热分析法发现南京浅表土样导热系数与干密度、含水率成正比；N. H. Abu-Hamde等[4](2001)通过热线法发现黏土颗粒含量较高的土壤导热系数较低.在土体导热性能的模型研究中，Johansen[5](1975)给出了饱和土、干土导热系数的计算公式；Lu等[6](2007)依据Johansen模型，提出利用土壤容重，石英含量和含水率预估导热系数；De Vries[7](1963)建立考虑温度影响的导热系数模型，并以石英砂为对象，研究不同温度下石英砂导热系数的变化规律，但对其他类型土不一定适用；Campbell et al.[8](1994)对不同质地、容重、含水量和温度的土壤样品进行导热系数测试，并对De Vries方程进行了修正，结果表明Campbell 模型对低温土体的模拟较好；de V-1 和 de V-2 模型[9]较为复杂，依赖界限含水率；Tarnawski[10](2002)提出15 ～ 30℃温度下，利用颗粒间接触传热修正系数加以增强的土壤颗粒间接触传热IPCHT(Inter-Particle Contact Heat Transfer)模型；Leong et al.[11](2005)提出热接触电阻TCR(Thermal Contact Resistance)，αtot，o作为传热修正系数，结果表明IPCHT模型有两个局限性，即在低含水率下Ke函数值为负值，在PWP附近和高温下对部分土壤导热系数预测较大.因此，有关导热系数的预测模型尚有一定的应用局限性.

本文利用热探针法测量了在较广温度范围(5～90℃)和较广体积含水率范围(风干状态～饱和状态)下上海浅层黏土的导热系数，对上海黏土采用修正后传质增强因子ξ的颗粒间接触传热(IPCHT)模型对该黏土的导热系数进行了预测，取得了较好的效果，该成果可为进一步核算该土体电缆载流量工作提供土体导热系数的取值参考.

1 实验材料及方法

1.1 试验材料

取扰动土进行试验研究，试验用土为上海浅层粉质黏土，取自上海奉贤区某一电力线路工程施工现场.该土样的基本工程参数及颗粒级配曲线分别见表1与图1.

表1 所使用黏土的物理参数Tab.1 Physical parameters of clay used

图1 颗粒级配曲线Fig.1 Grain grading curve

1.2 试验方法

前期试验准备的主要步骤如下：(1)将上海黏土自然风干、碾碎成粉末，过1 mm筛备用；(2)根据黏土干密度和模具体积，确定目标含水率土样所需加水量.使用喷瓶以保证水分润湿均匀，将土样装满半径为70 mm、高为52 mm的短圆柱容器[12],采用静态压力法压制成圆柱状土样；(3)完成制样后，为了消除环境温度波动对试件导热系数的影响，在养护和测试期间，试件均保持恒温(22±0.5℃)；(4)将恒温箱设置某一温度(5、20、40、60和90℃)，温度恒定后，采用恒体积容器固定土样，放于恒温箱中静置24 h.为保证测量过程中环境温度变化影响最小，实验室内温度维持在20℃[13],测量前检测土样的质量和体积，确保土样保存完善，密封性好.

图2 KD 2 Pro型热特性分析仪Fig.2 KD2 Pro thermal property analyzer

图3 导热系数测试过程Fig.3 Test process of thermal conductivity

如图2图3所示进行实验室测试，以测量大范围温度(5～90℃)范围内的导热系数.采用KD 2 Pro热特性分析器，本次试验为压实土样，为防止KD 2 Pro的测试探针损坏，预先使用电钻在样品中央进行钻孔加工.探针表面涂抹导热硅脂，在测定过程中用黑色胶布密封(参照图3).每10分钟重复3次测试，取平均值.相应温度的导热系数测试后采集探针插入的孔周围15 g的土壤样品，用干燥法测定水分.

2 试验结果及分析

2.1 含水率对导热系数的影响及原因

图4的结果表明非饱和上海黏土的导热系数随温度的升高而逐渐增大，在不同的温度下，体积含水率对导热系数的影响不同.当温度低于90℃时，导热系数随体积含水率变化的趋势较为一致：例如5℃条件下，在土样风干状态时(θw=3%)其导热系数为0.3 W·m-1·K-1；随着体积含水率增至8.6%，其导热系数快速增加为0.671 W·m-1·K-1；之后导热系数随含水率增加速率逐渐减小，而当土样达到饱和状态时，其导热系数又快速上升高至1.742 W·m-1·K-1.

土壤是岩石风化的产物，包括土壤颗粒、水和空气[14].在固液气三相中，气体的导热系数最小，20℃下气体的导热系数为0.002 3 W·m-1·K-1，而水的导热系数为0.55～0.68 W·m-1·K-1.干燥土体内的热量传输主要依靠颗粒间的点接触,以及空气参与的热量传输，所以土体在干燥状态下的导热系数较低.随着含水率的增加，土颗粒接触点表面形成液桥，通过增加粒子间的有效接触面积，大大提高了传热能力[15].另外，参与热量传输的水分比重增大，逐渐取代了土粒孔隙间导热系数相对较小的气体，从而使得土体的导热系数增加.液桥的形成和参与热量传输的水分的增加在低含水率下对土体的导热系数影响较大；继续增加水分,孔隙水的增加会削弱有效接触面对导热系数的影响,上述两因素的作用效应逐渐减弱，因此土体导热系数的增加速率逐渐变缓.而当土体含水率接近饱和状态时，其导热系数仍有较大增幅，原因是在土体逐渐饱和的过程中，孔隙水逐渐填满黏土集聚体内的孔隙，集聚体内的孔隙气体被取代，从而加快了热量的传递.

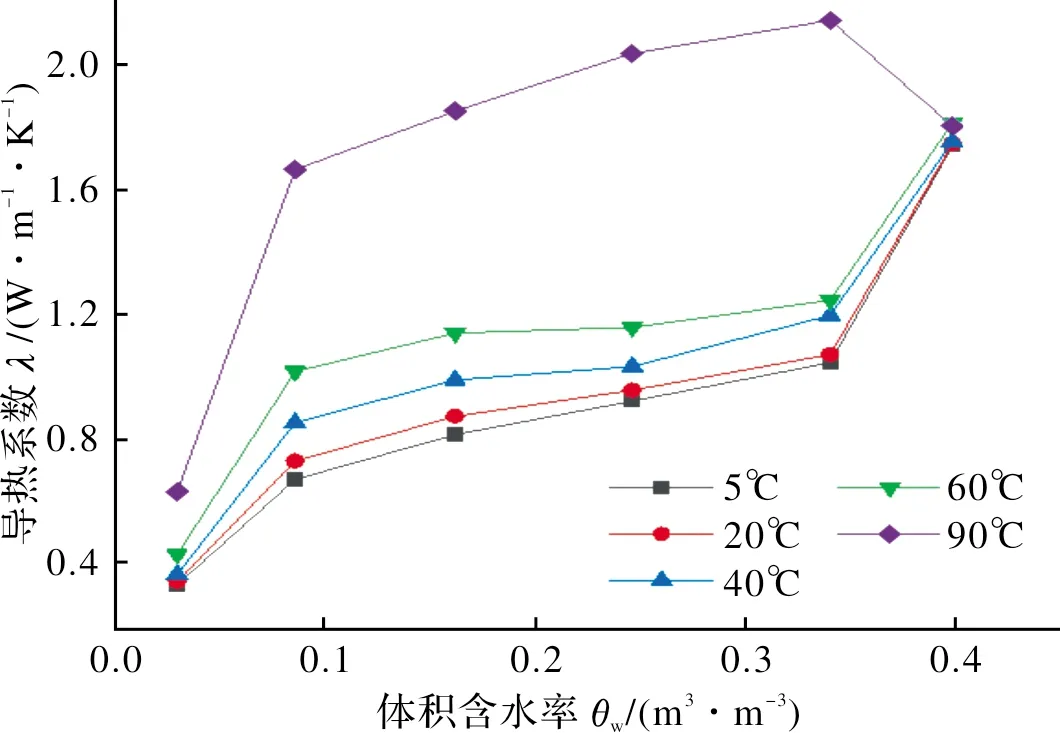
图4 土体导热系数随体积含水率的变化Fig.4 Variation of thermal conductivity of soil with volume moisture content

图5 土体导热系数随温度的变化Fig.5 Variation of thermal conductivity of soil with temperature

2.2 温度对导热系数的影响及原因

图5的结果表明非饱和上海黏土的导热系数随温度的升高而逐渐增大.中低温范围内(5～60℃)导热系数随温度升高出现较小增幅，而在高温范围内(60～90℃)导热系数随温度升高出现较大增幅.例如在土样θ = 20%时，其初始导热系数为0.922 W·m-1·K-1；随着温度升高至60℃，其导热系数缓慢增加为1.159 W·m-1·K-1；而当温度升高至90℃，其导热系数又快速上升至2.038 W·m-1·K-1.另外不同温度下饱和土样的导热系数比较接近，即温度对饱和土样的导热系数影响较小.

对于非饱和土，其导热系数随着温度的升高而逐渐增大.这主要是由于温度梯度的增大，土颗粒间存在的水桥(液岛)半月板促进了水汽的运动和潜热的传递.水汽潜热的定义是在高温下，土壤内部水分蒸发促进热传导的过程.Smits等[16](2013)认为随着温度的升高，导热系数的增加是以潜热形式进行的额外传热.他们也观察到潜热的传递增强了非饱和土的传热，从而增加了土体的表观导热系数.此外，潜热的传递需要水来形成液体岛以及土壤中具有足够的空气通道，使得水蒸气可以很容易地通过这些通道移动.这可以解释自然风干黏土的导热系数随温度的升高而变化不大的现象，因为没有足够的水来形成液体岛.此外，当温度为90℃时，接近饱和状态土样的导热系数反而逐渐下降，原因归因于高温时在非饱和状态下土体孔隙内水汽运动剧烈，产生的潜热传输效应影响较大，接近饱和状态时，由于传输路径阻断，这部分潜热传输效应减弱.

为研究潜热对导热系数的影响，Hiraiwa et al.(2000)[17]提出由潜热引起的导热系数与导热系数可以用接近0℃时的导热系数减去高于0℃时的导热系数来分离，研究水汽潜热传输效应的影响.提出水汽潜热传输产生的导热系数λv，温度对于土中液相和气相的导热影响较小，忽略5℃时的λv，用各温度下的导热系数与5℃时的导热系数之差Δλ，Δλ=λt-λ5，来表示水汽潜热传输的影响[18].

图6 Δλ随体积含水率和温度的变化Fig.6 Change of Δλ with volume moisture content and temperature

图6表示黏土潜热传输随含水率和温度的变化规律.由图6可知，上海粉质黏土水汽潜热传输运动的剧烈程度与温度有关，温度越高，水汽潜热效果越明显.在土体风干和饱和两种情况下，水汽潜热效果较小.原因是含水率较低的情况下可参与潜热传输的水汽较少；而饱和情况下水汽潜热传输的空间受限.因此水汽潜热传输效应在两端最微弱.这也就解释了为什么黏土导热系数会随含水率和温度升高而逐渐增大.

3 不同温度下黏土的导热系数模型预测

De Vries导热系数模型考虑温度的影响，但对其他类型土不一定适用.Campbell模型反映了含水率、温度与土体导热系数的关系，但对高温土体的预测并没有那么准确.de V-1和de V-2模型两个改进模型涉及参数众多，且依赖界限含水率.

IPCHT模型以自洽近似理论模型为基础，即将土分解为由固液气三相构成的介质.假定各单相分散在等效均质的连续基体中，由自洽近似理论模型推求出三相介质的等效导热系数λeff.因此提出考虑传质增强因子ξ的颗粒间接触传热(IPCHT)修正模型，考虑到温度变化范围较大，等效导热系数λeff分为两种情况:

(1)

(2)

(3)

Ke=0.7logSr+1.0(Sr>0.05)

(4)

λda=2.454×10-2+7.27×10-5t

(5)

λ2=0.569+1.884×10-3t-0.772×10-6t2

(6)

(7)

(8)

式中:λ1，θ1为土中固相的导热系数及体积分数；λ2，θ2为土中液相的导热系数及体积分数；λ3，θ3为土中气相的导热系数及体积分数;ξ为传质增强因子；t为摄氏度(℃)；λda为干燥空气导热系数；λs为土体固相颗粒导热系数;Ke为Kersten系数，Sr为饱和度；λq为石英导热系数，参考De Vries[7](1963)取8.8 W·m-1·K-1;θq为石英体积分数；λo为其他矿物的导热系数，参考刘晨晖等[19](2011).由计算可知，上海黏土固相颗粒导热系数λs为4.86 W·m-1·K-1；ψ为水势(kPa);MW为水的摩尔质量；ρW为水的密度(103kg·m-3);R为绝对气体常数；T为开尔文氏温度(K);Pb，Pvs分别为大气压和饱和蒸汽压(kPa)；gl(l=-1～4)为形状因子，g-1=-0.58×104；g0=1.39；g1=-0.05；g2=0.42×10-4；g3=-0.14×10-7；g4=6.5.由叶为民[20-21](2005)上海粉质黏土的土水特征曲线推求土中水势ψ.

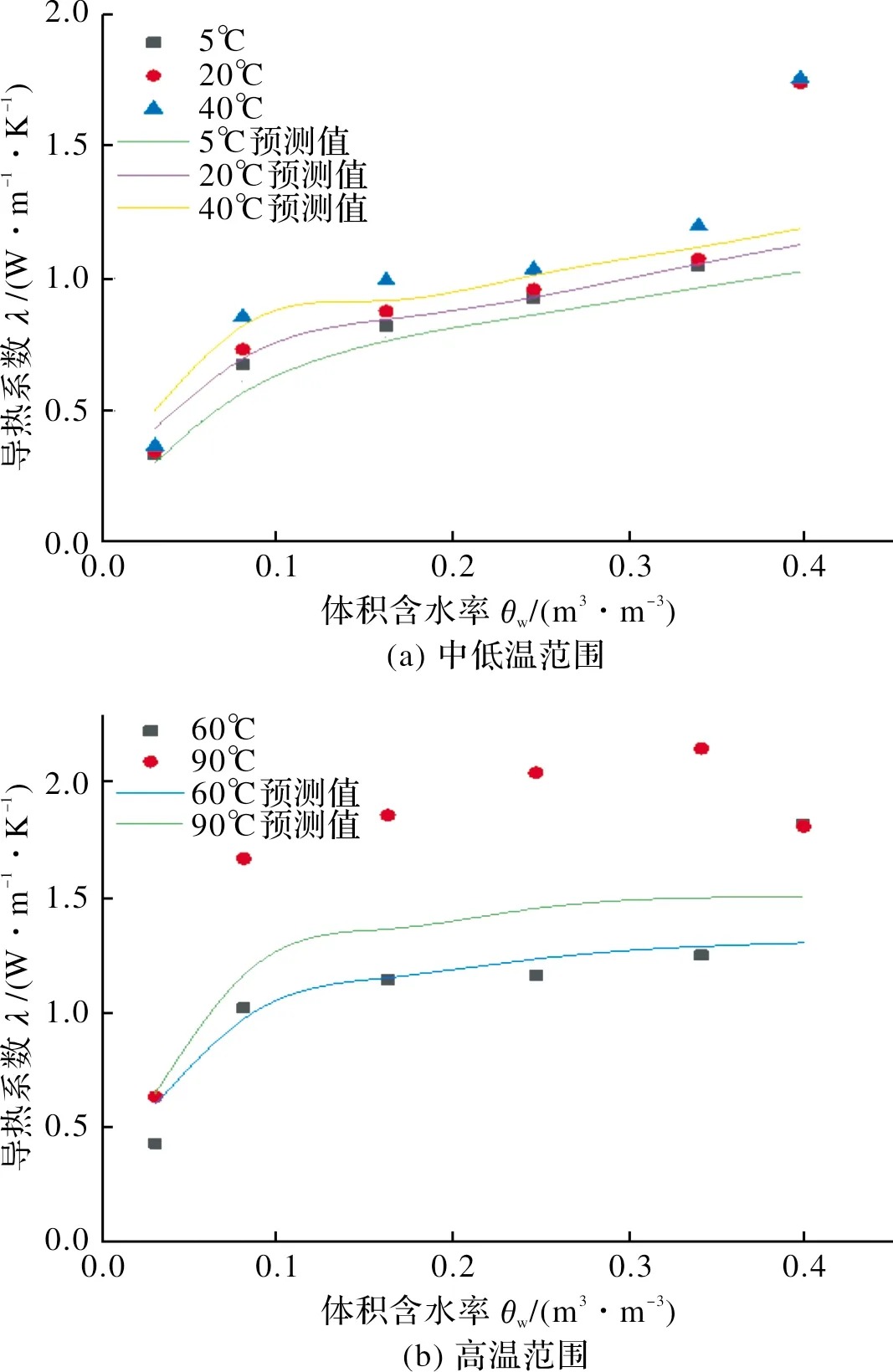
图7 不同温度下土壤导热系数测定值与预测值的比较Fig.7 Comparison of measured and predicted values of soil thermal conductivity at different temperatures

图7表示未经修正的IPCHT模型在不同温度下土壤导热系数测定值与预测值的比较结果.由图可知，非饱和黏土在低于90℃下的导热系数的测定值与预测值符合程度较高；90℃时导热系数的预测曲线与实测曲线出现较大差值.而不同温度下的饱和黏土，实测值与预测值略有差异，说明未经修正的IPCHT模型对低于90℃的非饱和土拟合效果较好.笔者认为，上海黏土试样在高温时潜热效果较明显，而未经修正的IPCHT模型没有考虑潜热的影响，因此预测值会低于实测值.所以上海黏土在90℃的等效导热系数需考虑传质增强因子ξ，根据上海黏土土壤质地取2.5.

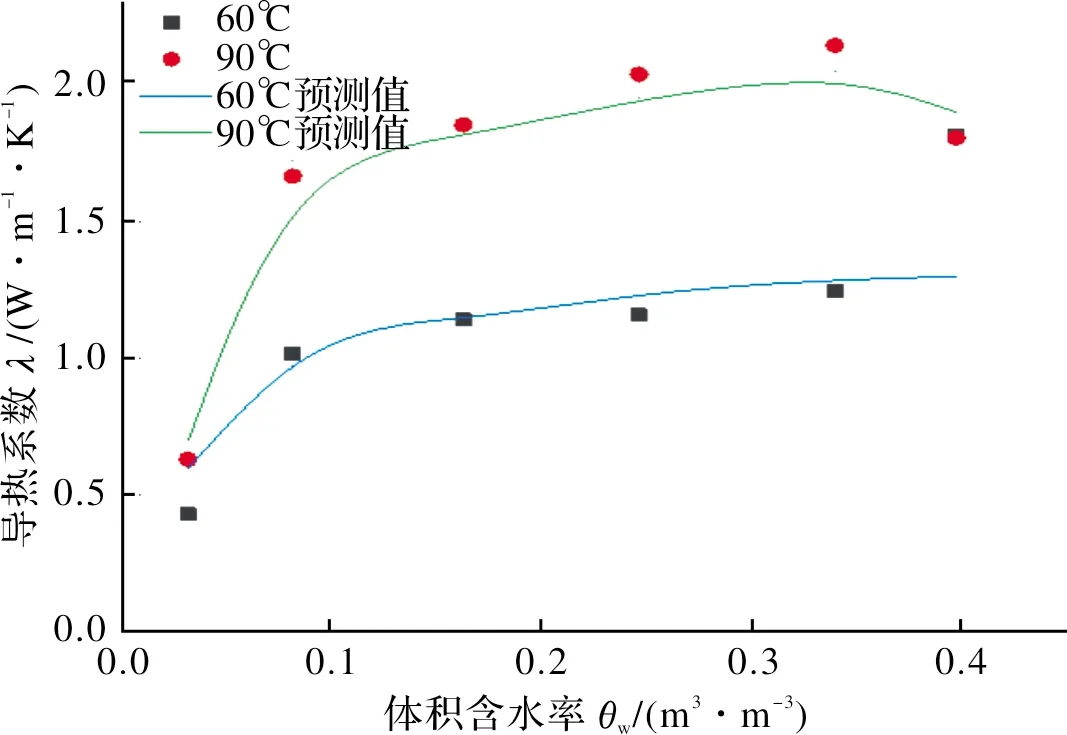
图8 经传质增强因子修正后实测值与预测值的比较Fig.8 Comparison between measured value and predicted value after mass transfer enhancement factor correction

此外，使用均方根误差(RMSE)对模型进行了评价:

(9)

式中，λexp为实测值;λpre为预测值.

图8为经传质增强因子修正后实测值与预测值的比较.由图可知，经传质增强因子ξ修正后，90℃时上海黏土导热系数预测值和实测值相符地较好，非饱和黏土土模型修正后均方根误差为20%.而对于饱和上海黏土，IPCHT模型的预测效果不是很理想，因此寻找适合饱和上海黏土导热系数的模型，建立不同温度下上海黏土导热系数与电缆载流量的有限元模型是下一步的研究目标.

4 结论

(1)随体积含水率的增加，上海粉质黏土在低于和等于90℃时导热系数出现了明显不同的趋势.第一种情况是和大多数学者发现的规律类似，由于液岛的形成和水汽潜热传输的影响黏土的导热系数随温度的升高而逐渐增大；第二种情况是高温下黏土导热系数出现了先增后降的情况.归因于高温时在非饱和状态下土体孔隙内水汽运动剧烈，产生的潜热传输效应影响较大，接近饱和状态时，由于传输路径阻断，潜热传输效应减弱.

(2)传统意义上研究土体导热系数的主体为非饱和土，而本文考虑了土体饱和情况下的导热系数，结果表明由于饱和土的孔隙体积无法为水汽潜热传输提供路径，温度的变化对导热系数的影响并不明显.未经修正的IPCHT预测模型对低于90℃的非饱和粉质黏土拟合效果较好，而90℃时模型的预测值和实际值有偏差，经过传质增强因子修正后符合工程要求.

(3)修正后的IPCHT模型对于非饱和土体的导热系数拟合效果较好，而对于饱和上海黏土导热系数的预测不是很理想，解决这个问题的关键是找到从众多模型中找到适合饱和上海粉质黏土导热系数的模型，必要时需自己建立方程来拟合.因此建立不同温度下饱和上海黏土导热系数模型与电缆载流量的有限元模型是下一步的研究目标.