基于FMI仿真系统的优化代数环求解算法
宋欢儒 田野 臧晶 冷丰汐
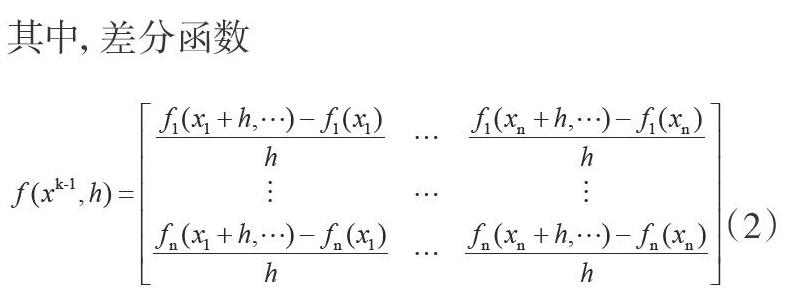


摘 要:随着仿真技术的发展,仿真模拟验证越来越重要。然而多学科仿真致使仿真过程中产生的代数环问题还未得到重视。为了解决联合仿真中的代数环问题,该文对牛顿下山法进行优化,通过替换雅可比矩阵提高计算速度,并将算法应用在FMI联合仿真系统中,成功验证了优化后的代数环求解算法的有效性与实用性。
关键词:FMI仿真系统 代数环 牛顿下山 求解算法
中图分类号:TP393.08 文献标识码:A文章编号:1672-3791(2021)05(b)-0053-03
Abstract: With the development of simulation technology, the simulation verification of actual industrial products is becoming more and more important. However, the problem of algebraic loop caused by multidisciplinary simulation has not been cared by most people. This paper optimized the Newton Downhill method to improve the calculation speed by replacing the Jacobian Matrix to solve the algebraic ring problem in the co-simulation, and applied the algorithm in the FMI co-simulation system, and successfully verified the effectiveness and practicability of the optimized algebraic ring solving algorithm.
Key Words: FMI Simulation System; Algebraic loop; Newton downhill method; Solution Algorithm
FMI标准的联合仿真技术已被许多仿真软件所使用,仿真过程中的代数环问题求解方案中,求解时间较长影响仿真速度。该文通过对代数环求解算法进行优化,替换需要较长计算时间的雅可比矩阵,并将优化算法应用在FMI仿真系统中,在解决代数环问题的同时,提高仿真速度[1-2]。
1 优化代数环求解算法设计
联合仿真过程中的代数环问题就是由仿真模型之间的耦合关系造成的,即为各模型之间的连接构成环路,无法确定输出输入顺序的问题[3]。将其解析为数学问题即为对非线性方程组的求解问题[4]。该文设计牛顿下山法对非线性方程组进行求解[5-6],整个流程分为3个部分:一是对各参数、变量进行定义与设计;二是符合下山条件后的迭代计算;三是不符合下山條件后通过修正向量值直至达到下山条件要求。算法流程图见图1。
使用python语言对牛顿下山代数环求解算法进行仿真方法设计,具体如下。
(1)设计main( )主函数,可修改函数中所存储的方程组内容,包括方程组等式、向量等。
(2)设计down( )函数,完成定义变量、设计求解表达式中包含差分函数等函数表达式。
(3)设计done( )函数,实现牛顿下山算法过程中的下山判决及对非线性方程组求解的迭代循环。
设计差分方法对原算法中的雅可比矩阵进行替换,即为该文的优化代数环求解算法。优化后的求解迭代式为:
2 仿真与分析
为了验证该文设计的优化代数环求解算法的正确性及高效性,将算法应用在FMI仿真系统中进行模拟验证,并对仿真结果进行分析。将仿真模型飞行员、风模型、变体制动器、飞行器动态模型、控制器连接成仿真模型耦合图,具体见图2。对变体制动器的输出端口2进行仿真结果分析。提示仿真模型耦合图中含有代数环结构提示,具体见图3。
未优化的代数环求解算法仿真结果见图4,优化后的代数环求解算法仿真结果见图5。
将仿真过程中后台的仿真日志进行截取,对优化前后的代数环求解算法的计算时间进行对比见图6、图7。
对比两次仿真结果,可以看出优化后的代数环求解算法可以对代数环问题进行正确求解;且优化后的代数环求解算法的计算时间为0.548 080 s,比未优化时所用的时间0.697 038 s短。因而可验证该文设计的基于FMI仿真系统的代数环求解算法的正确性和高效性。
3 结语
该文首先对FMI仿真系统仿真过程的代数环问题进行阐述,提出利用牛顿下山法的代数环求解算法,并在原有算法基础上对其进行优化,设计差分函数替换雅可比矩阵从而提高算法的计算速度。最后在FMI仿真系统中对含代数环结构的仿真模型耦合系统进行仿真模拟验证,通过对仿真结果及后台日志数据的对比,为代数环求解算法的正确性提供了验证。
参考文献
[1] 郭永.编队飞行航天器有限时间协同控制[D].哈尔滨工业大学,2016.
[2] 胡全义.基于键合图的多领域统一建模与仿真技术研究[D].大连理工大学,2017.
[3] 李志鹏,马龙祥,孟旭,等.基于Matlab的SAW模态耦合模型的仿真研究[J].重庆理工大学学报:自然科学版,2018,32(4):10-15.
[4] 王静,孙春虎,方愿捷.基于牛顿迭代控制的分区动态无功补偿建模与仿真[J].巢湖学院学报,2020,22(6):104-114.
[5] 冷丰汐,陈永恒.一种求解代数环问题的python仿真实现方法[J].电子世界,2020(15):93-94.
[6] 王乐成,赫亚兰,韩新丽,等.对牛顿迭代法的改进[J].高师理科学刊,2020,40(3):23-26.

